
MILP-based Approach for Optimal Implementation of Reconfigurable
Real-time Systems
Wafa Lakhdhar
1
, Rania Mzid
2,3
, Mohamed Khalgui
1,5
and Nicolas Treves
4
1
LISI Lab INSAT, University of Carthage, INSAT Centre Urbain Nord BP 676, Tunis, Tunisia
2
ISI, University Tunis-El Manar, 2 Rue Abourraihan Al Bayrouni, Ariana, Tunisia
3
CES Lab ENIS, University of Sfax, B.P:w.3, Sfax, Tunisia
4
CEDRIC Lab, CNAM, 292 rue Saint-Martin, Paris, France
5
SystemsControl Lab, Xidian University, August Bebel Str 70, Halle, China
Keywords:
Embedded System, Reconfigurable Architecture, Real-time Scheduling, Linear Programming, Posix-based
Implementation.
Abstract:
This paper deals with the design and implementation of reconfigurable uniprocessor real-time embedded sys-
tems. A reconfiguration is a run-time operation allowing the addition-removal of real-time tasks or the update
of their parameters. The system is implemented then by different sets of tasks such that only one is executed at
a particular time after a corresponding reconfiguration scenario according to user requirements. The problem
is to optimize the system code while meeting all related real-time constraints and avoiding any redundancy
between the implementation sets. Based on the Linear Programming (MILP), we propose a multi-objective
optimization technique allowing the minimization of the number of tasks and their response times. An opti-
mal reconfigurable POSIX-based code of the system is manually generated as an output of this technique. We
apply the paper’s contribution to the study of the performance evaluation.
1 INTRODUCTION
A real-time system is any system which has to re-
spond to externally generated input stimuli within a
finite and specified delay (Burns and Wellings, 2009).
The development of real-time systems is not a triv-
ial task because a failure can be critical for the safety
of human beings (Cottet and Grolleau, 2005). The
researchers are moving today toward proposing tech-
niques for programming concurrent reconfigurable
real-time systems.
To provide design-time guarantees on timing con-
straints, different scheduling methodologies can be
used, such as Rate Monotonic (RM) which is a
scheduling algorithm which was defined by Liu and
Layland (Liu and Layland, 1973) where the prior-
ity of tasks is inversely proportional to their peri-
ods. The authors of (Bouaziz et al., 2015) provide
a method to drive the designer by producing a set of
design solutions based on RM scheduling algorithm.
In (Mehiaoui et al., 2013; Wo
´
zniak, ), the authors
are interested in the optimization of deployment tech-
niques from functional and platform models of real-
time systems by using mixed integer linear program-
ming (MILP). An MILP formulation is easily exten-
sible, re-targetable to a different optimization metric
and can easily accommodate additional constraints or
legacy components (Mehiaoui et al., 2013). There are
many programming languages designed for the devel-
opment of real-time systems such as POSIX (Portable
Operating System Interface) (Lewine, 1991). The
POSIX standard promotes portability of applications
across different operating system platforms. The au-
thors (Obenland, 2000) use POSIX in the develop-
ment of software for real-time and embedded sys-
tems.
The synthesis of a valid and optimal implementation
model consists in building the set of tasks implement-
ing the applicative functions while meeting all related
real-time constraints. The reconfiguration at the im-
plementation level consists in adding/removing tasks
or modifying their timing parameters to go from one
implementation to another, which may require an ad-
ditional time for reconfiguration. So that, the resulting
implementation model should avoid redundancy be-
tween the different implementations to minimize the
possible overhead.
In this paper, we present an approach toward an op-
330
Lakhdhar, W., Mzid, R., Khalgui, M. and Treves, N.
MILP-based Approach for Optimal Implementation of Reconfigurable Real-time Systems.
DOI: 10.5220/0006006703300335
In Proceedings of the 11th International Joint Conference on Software Technologies (ICSOFT 2016) - Volume 1: ICSOFT-EA, pages 330-335
ISBN: 978-989-758-194-6
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

timal implementation of reconfigurable uniprocessor
real-time systems. The proposed approach aims to au-
tomatically produce a valid and optimal task model
from a given specification. The task model consists of
a set of tasks implementing the applicative functions
that we assume independent and periodic. We assume
also that assigning priorities to tasks is performed us-
ing rate monotonic algorithm RM (Klein et al., 1993).
The paper is organized as follows. Section 2 gives
an overview on related works. Section 3 provides the
formalisation of approach. Section 4 explains in de-
tails the proposed approach to obtain a valid and op-
timal implementation model from the user specifica-
tion. Section 5 illustrates the approach on the chosen
case study and evaluates its efficiency. Finally, we
summarize our work and discuss the future work in
Section 6.
2 RELATED WORKS
In this section, we present the related works that deal
with real-time systems and reconfigurable architec-
tures.
In the literature, many approaches have been car-
ried out in the area of schedulability analysis for meet-
ing real-time requirements. Pillai and Shin (Pillai
and Shin, 2001) propose an optimal algorithm for
computing the minimal speed that can make a task
set schedulable. Concerning the system model and
the optimization objectives, the proposed approach is
closely related to the research works in (Bertout et al.,
2014; Bouaziz et al., 2015; Mehiaoui et al., 2013). In
(Bertout et al., 2014), the authors propose a technique
to minimize the number of tasks in a real-time system
while satisfying timing constraints. The approach in
(Bouaziz et al., 2015) aims both to reduce the num-
ber of preemptions for minimizing timing overheads
and to maximize the laxity of tasks in order to im-
prove the schedulability of the design model. There
are also related approaches which generate complete
real-time systems. In (Pillai and Shin, 2012), the au-
thors deliver an approach called TASTE to enable the
generation of a complete real-time distributed system.
The authors in (Pagetti et al., 2011) provide a frame-
work that allows designers to automatically generate
by the Prelude language, a set of real-time tasks that
can be executed on a uniprocessor architecture.
Nowadays, many research works have been pro-
posed to develop reconfigurable systems. The authors
in (Gharsellaoui et al., 2012) propose an approach that
deals with reconfigurable systems to be implemented
with different tasks under deadline constraints accord-
ing to user requirements. In (Krichen et al., 2010),
the authors aim to provide an automated development
process from modeling to implementation for the dy-
namic software part of reconfigurable systems.
There are many programming languages designed
for the development of real-time systems. Among
the most used real-time languages, we cite real-time
java (RT-java) which aims to support the program-
ming of real-time codes from different directions used
by other software development platforms. POSIX
(Portable Operating System Interface) is a standard
written in terms of the C programming language.
(Lewine, 1991). This standard facilitates the applica-
tion portability that is why we adopt it as a target lan-
guage to implement a reconfigurable real-time system
in the current paper.
The main contributions of this paper are four-fold.
The first part consists in ensuring the respect of tim-
ing properties before the effective implementation of
the real-time system (i.e. at the design level). Sec-
ond, we are interested in the reconfiguration of real-
time systems where the addition and removal of tasks
are applied at run-time. Third, we propose a multi-
optimization metric. Indeed, the proposed approach
aims to minimize the reconfiguration time by avoid-
ing a redundancy between the different implementa-
tions from one side. From the other side, it aims to
minimize the response times of the real-time tasks in
order to maintain the performance of the system. The
fourth part, this work automatically generates a com-
plete reconfigurable real-time system from the spec-
ification level by using the programming language
POSIX. None of the existing works is solving all the
four problems together.
3 SYSTEM FORMALIZATION
In this section, we present a formal description of a re-
configurable uniprocessor system. We present in ad-
dition real-time prerequisites required to introduce the
paper’s contribution.
It is assumed in this work that a reconfigurable
real time system Sys is defined as a set of implemen-
tations: S ys = {imp
1
,imp
2
...imp
m
}. We denote by
Sys(t) the implementation defining the system at a
particular time t (i.e. Sys(t) = imp
i
). An implemen-
tation imp
i
is composed of n tasks that we assume in-
dependent and periodic (i.e. imp
i
= {τ
1
,τ
2
,τ
3
...τ
n
}).
Each task τ
i
executes a set of applicative functions
τ
i
= {F
1
,F
2
,F
3
...F
k
}. A function F
i
is character-
ized by static parameters F
i
= (T
f
i
,C
f
i
) where T
f i
is
the activation period of the function F
i
and C
f i
is an
estimation of its worst case execution time WCET.
Note that these parameters are considered as inputs
MILP-based Approach for Optimal Implementation of Reconfigurable Real-time Systems
331
to the proposed approach and must be specified by
the user. Each task τ
i
is characterized by a set of real-
time parameters (r
i
,T
i
,C
i
,D
i
,P
i
) : its release time r
i
,
we assume that r
i
= 0, its activation period T
i
which
is deducted from the activation periods of the func-
tions implemented by this task, its capacity or worst
case execution time C
i
which is equal to the sum of
the WCETs of the functions executed by this task, its
deadline D
i
we assume that D
i
= T
i
, the priority P
i
, we
assume that P
i
= 1/T
i
since we adopt the Rate Mono-
tonic priority assignment(RM).
Let U be the processor utilization factor defined by:
U =
∑
n
i=1
C
i
T
i
. We perform Rate-Monotonic (RM) re-
sponse time analysis based on the computation of an
upper bound of the response time Rep
i
of the different
tasks constituting the task model. This analysis aims
to verify whether these tasks complete their computa-
tions within the time limit specified by the real-time
application i.e. the deadline (Rep
i
≤ D
i
)(Klein et al.,
1993). The reconfiguration scenario corresponds to
adding/removing tasks or modifying timing param-
eters. Thus, we introduce the reconfiguration time
T
recon f
which refers to the time required to jump from
one implementation to another according to user re-
quirements (i.e. reconfiguration conditions). This pa-
rameter is defined as follow:
T
recon f
= A ∗ T
delete
+ B ∗ T
creat
Where A is the number of deleted tasks, B is the
number of created tasks, T
delete
is the spent time to
delete a task and T
creat
is the spent time to create a
task. We assume that the blanking time T
delete
and
creation time T
creat
of all the tasks are equals for a
considered platform (i.e. T
delete
= T
creat
). We denote
by T
cost
the spent time to create a task or to delete it
(i.e. T
delete
= T
creat
= T
cost
). Thus, the reconfiguration
time is given as follow:
T
recon f
= (A + B) ∗ T
cost
4 PROPOSED APPROACH
In this section, we present an overview on our ap-
proach and detail the structure of different modules
involved in this work. We deliver an approach which
automatically converts a high-level specification of
a reconfigurable real-time system into an executable
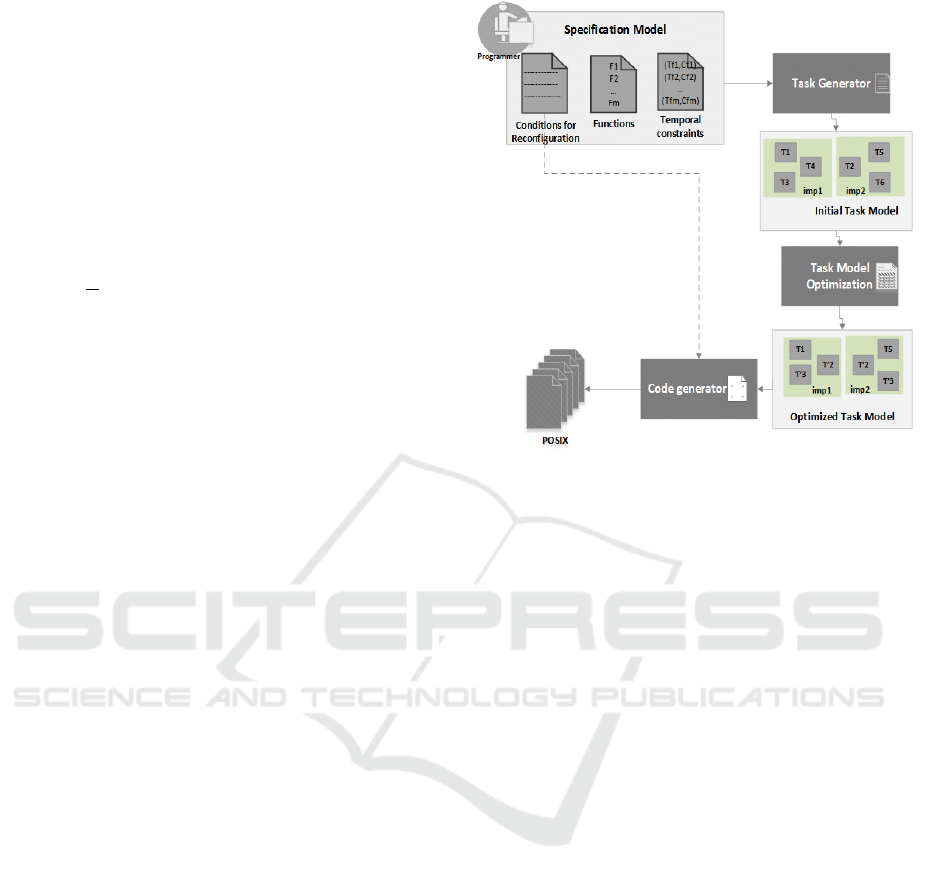
running on POSIX platform. Figure 1 shows the pro-
cess of the proposed approach. As entry, the designer
provides the specification model which defines the
reconfiguration conditions, the applicative functions
that must be executed under a considered condition
and the temporal parameters of each function. This
model presents the input of the task generator step
which aims to produce an initial task model. Then,
Figure 1: Process overview.
the optimization step receives the generated model
and proposes a valid and optimal task model. This
model is finally converted into an executable program
running under POSIX.
4.1 Task Generator
The first step consists in generating the initial task
model. This stage considers the specification model
as an input and aims to generate the initial task model
which defines a possible implementation of the con-
sidered system. For each reconfiguration condition,
this step generates an implementation and associates
its appropriate functions. Then, for each generated
implementation, it regroups the functions having the
same period T
f i
to be executed by one task τ
i
. Since
we assume that the release time r
i
= 0 and P
i
= 1/T
i
,
the task τ
i
is characterized only by (T
i
,C
i
,D
i
) where
the period T
i
corresponds to the period of the grouped
functions, C
i
is the sum of WCETs of the grouped
functions and the deadline D
i
of each task is equal to
the corresponding period T
i
. Let us note that for the
generation of this model, the optimization and real-
time feasibility concerns are not considered.
4.2 Task Model Optimization
This phase aims to produce a feasible and optimal im-
plementation of the reconfigurable real-time system
from the initial task model.
In order to avoid redundancy between the sets of im-
plementation and reduce the number of tasks, this
ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications
332

phase aims to merge the tasks belonging to differ-
ent implementations but implementing the same func-
tions and/or having the same periods. To implement
properly the problem by taking into consideration the
different constraints, we propose a MILP formulation
of our problem. So we should define the objective
function and the required constraints for parameters
and variables.
Definitions. Let m be the number of tasks in the ini-
tial model, let N be the number of tasks in the new
task model, let s be the starting time which corre-
sponds to effective starting time of each task. We de-
note by InitTask the initial task model which is a three
column matrix where the first column presents the pe-
riod T
i
of task, the second one presents their WCETs
C
i
and the third column is their deadline D
i
. NewTask
is the resulting task model after merging the different
tasks (i.e. optimized task model).
Objective Function.
Maximize
∑
i, j∈{1,m}
Merge
i j
−
∑
i, j∈{1,m}
Rep
i j
(1)
This expression defines the objective function of our
problem. Merge denotes a boolean variable used
to mention whether two tasks τ
i
and τ
j
are merged.
More in detail, Merge
i j
is equal to 1 if task t
i
∈ imp
k
and task t
j
∈ imp
l
are merged. The expression(1)
aims to maximize the number of merged tasks and
minimize the sum of response times of the different
tasks constituting the task model. In order to limit non
meaningful merging situations, we define in addition
the following constraints:
Merging Situation Constraints.
The constraints (2) and (3) introduce the merging con-
dition such as tow the tasks τ
i
∈ imp
k
and τ
j
∈ imp
l
will be merged if they have the same period.
∀i, j ∈ {1 .. .m} et i 6= j,
i f (InitTask[i,1] − InitTask[k, 1]) = 0 then Merge
i j
= 1
(2)
∀i, j ∈ {1 .. .m} et i 6= j,
i f (InitTask[i,1] − InitTask[k, 1]) 6= 0 then Merge
i j
= 0
(3)
The constraint (4) means that we have to maximize
the number of merged tasks and thus minimize the
number of tasks used in the task model. Indeed, this
equation serves as a bound for the objective function
(i.e. the number of merging operations).
N = m − (
∑
i, j∈{1...m}
Merge
i j
)/2 (4)
Real-time Constraints.
NewTask is a three column matrix where the first col-
umn presents the periods of the new tasks computed
by the constraint (5). The second column presents the
WCETs of the tasks computed by the constraint (6)
and the last column is the deadline presented by the
constraint (7)
∀k ∈ {1 .. .N},∀i ∈ {1 ... N} : NewTask[k, 1] = InitTask[i, 1]
(5)
NewTask[i,2] = (InitTask[i,2]+InitTask[ j,2])Merge[i, j]+
(1 − Merge[i, j])InitTask[i,2] (6)
∀i ∈ {1 . . . N},NewTask[i,3] = NewTask[i,1] (7)
The constraint (8) verifies whether the new model
meets the timing constraints.
U =
N
∑
i=1
NewTask[i,2]
NewTask[i,1]
≤
N
∑
i=1
N(2
1
N
− 1) (8)
Constraint (9) ensures that the response times Rep
i
of
the different tasks in the optimized model are lower
or equal than their deadlines:
∀i ∈ {1 . . . N}Rep
i
≤ NewTask[i,3] (9)
Constraint (10) gives the computation formula of the
response time Rep
i
of task τ
i
:
Rep
i
= s[i] + NewTask[i,2] (10)
The response time Rep
i
of a task τ
i
is defined as the
sum of its start time and its execution time.
∀i ∈ {1 . . . N}s[i] − s[ j] >= NewTask[ j,2] (11)
∀i ∈ {1 . . . N}s[ j] − s[i] >= NewTask[i,2] (12)
To ensure a single executed task at any time, we
should have either
s[i] − s[ j] − NewTask[ j,2] >= 0 or s[ j] − s[i] −
NewTask[i,2] >= 0, for every pair of tasks t
i
and t
j
.
∀i ∈ {1 . . . N}s[i] <= r[i] (13)
The task model generated by the linear program will
be interpreted by the code generator in order to gen-
erate a running program in POSIX.
4.3 Code Generator
The last step of our approach consists in building
the executable application from the optimized task
model. We manually generate a POSIX code on the
basis of transformation rules. For each task in the op-
timized task model, the code generator implements a
POSIX thread by using pthread. In addition, this step
produces the controller code of the reconfigurable
real-time system, which allow moving from imple-
mentation to another, following well-defined condi-
tions (i.e. user requirements).
MILP-based Approach for Optimal Implementation of Reconfigurable Real-time Systems
333
5 CASE STUDY
In this section, we illustrate the proposed approach
through a case study. The considered case study con-
sists in a Global Positioning System (GPS). Firstly,
we present the GPS specification. Then we apply
the proposed approach to an automatic construction
of a feasible and optimal implementation of a recon-
figurable real-time system.
5.1 GPS Presentation
The global positioning system (GPS) is used to define
the position of an object on a plan or a map using the
information provided via radio signals by the associ-
ated satellites.
To show the applicability of our approach, we con-
sider in this paper a simplified version of this system.
For clarity, several features of the system (GPS) were
omitted. Therefore, we only define two modes of op-
eration:
Insecure Mode:
This mode is defined by seven functions:
(i) F
1
: Co ntrolBase used to synchronize the satel-
lite clock,
(ii) F
2
: GpsSatellite used to send radio signals (ana-
logue) terminal,
(iii) F
3
: Position used to receive the satellite signal,
(iv) F
4
: Receiver used to convert the analogue signal
into a digital signal,
(v) F
5
: Decoder used to decode the digital informa-
tion and separate the information of calculating
the distance from time information,
(vi) F
6
: TreatmentUnit used to calculate the distance
of the satellite and determine position.
(vii) F
7
: Encoder used for encoding information of
time and position.
Secure Mode:
The secure mode is defined by eight functions.
Compared with the insecure mode, we have replaced
the function Position by Position Secure function
noted F
0
3
and we added AccessController function F
8
to ensure the secure reception of radio signals.
5.2 GPS Initial Task Model
The second step consists in generating the implemen-
tations and their tasks from the specification model by
applying the Algorithm. We obtain two possible im-
plementations of the GPS which refer respectively to
the two execution modes already specified.
5.3 GPS Optimized Task Model
The third step corresponds to the generation of the
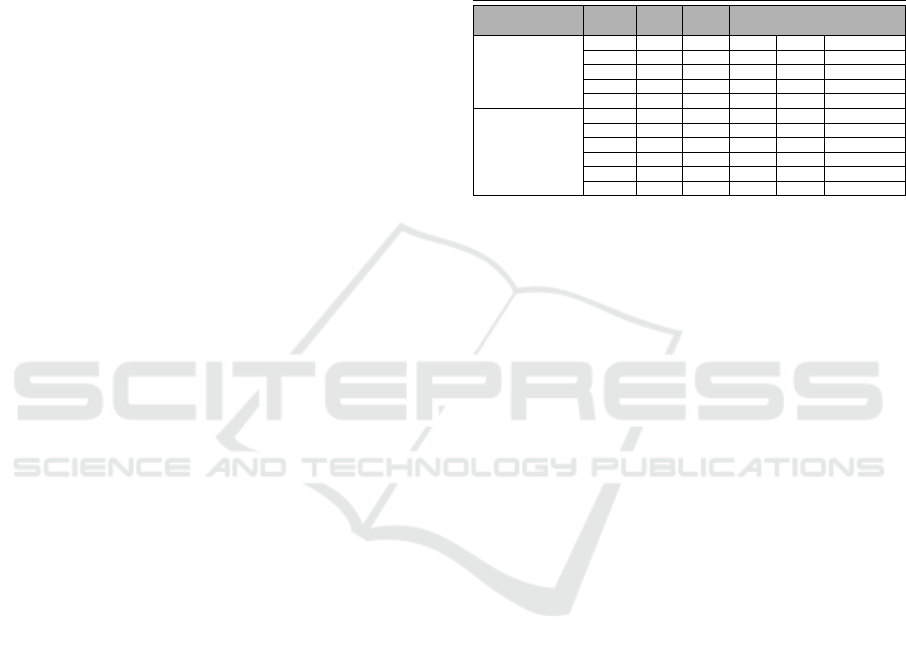
optimized task model from the initial one. A tabular
description of the task model generated by this phase
is given in Table 1.
We can see from Tables 1, this model satisfies the
Table 1: Tabular description of the optimized task model of
the GPS.
Execution mode Task T
i
C
i
D
i
Rep
i
Function
(ms) (ms) (ms) (ms)
τ
1
100 50 100 80 F
1
τ
0
2
200 40 200 200 F
2
Insecure Mode
τ
0
3
300 140 300 280
F
3
,F
0
3
,F
4
τ
0
4
400 100 400 360 F
5
,F
6
τ
0
5
500 60 500 450 F
7
τ
6
100 60 100 50 F
1
τ
0
2
200 40 200 200 F
2
τ
0
3
300 140 300 280
F
0
3
,F
4
Secure Mode
τ
0
4
400 100 400 360 F
5
,F
6
τ
0
5
500 60 500 450 F
7
τ
11
600 50 600 500 F
8
timing constraints of the GPS system since the re-
sponse times Rep
i
of the different tasks are lower than
their deadlines D
i
.
5.4 Performance Evaluation
We denote by T
recon f
initial
the reconfiguration time in
the initial task model of the GPS and T
recon f
Current
the
reconfiguration time in the optimized task one. These
parameters are given as follow:
T
recon f
initial
= 5 ∗ T
delete
+ 6 ∗ T
creat
= 11 ∗ T
cost
T
recon f
Current
= 1 ∗ T
delete
+ 2 ∗ T
creat
= 3 ∗ T
cost
We note that the proposed approach allows to re-
duce the reconfiguration time and thus improves the
overall performance of the reconfigurable real-time
system (GPS). It minimizes also the sum of the re-
sponse times of the all considered tasks such as
Rep
initial
= 3010 ms and after optimization it becomes
Rep
optimized
= 1920 ms . In addition, we have ran-
domly generated instances with 5 to 40 tasks. We
compare the reconfiguration time and the sum of re-
sponse times after optimization with the initial corre-
sponding parameters. The numerical results are de-
picted in figures 2 and 3:
These figures show that the optimization of the re-
configuration and response times are clearer and more
important for large scale reconfigurable real-time sys-
tems.
6 CONCLUSION
In this paper, we have proposed an approach to sup-
port the development of reconfigurable real-time sys-
ICSOFT-EA 2016 - 11th International Conference on Software Engineering and Applications
334
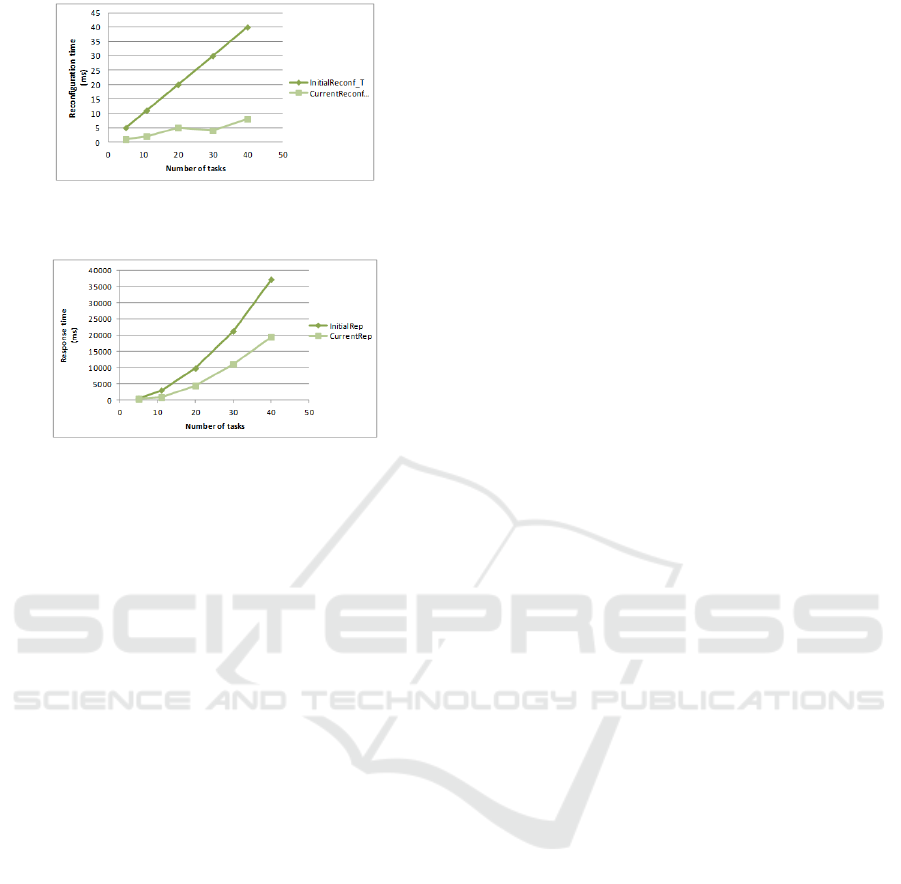
Figure 2: Comparison between Current reconfiguration
time and initial one.
Figure 3: Comparison between Current response time and
initial one.
tems. This approach consists in defining the speci-
fication such as reconfigurable conditions, functions
and temporal constraints, then it generates an initial
task model. After that, a MILP integral formulation
is provided to compute the optimal solution for min-
imizing redundancy. Finally, the proposed approach
generates a POSIX-based program describing the re-
configurable real-time system. We have evaluated the
performance of the three-step approach. The numeri-
cal results show that the integer programming model
allows to minimize the reconfiguration time and re-
sponse times.
As a future work, we aim to extend our approach by
considering multiprocessor systems and other opti-
mization metrics. So that we expect to evaluate scal-
ability of the proposed method with an industrial ex-
ample.
REFERENCES
Bertout, A., Forget, J., and Olejnik, R. (2014). Minimiz-
ing a real-time task set through task clustering. In
Proceedings of the 22nd International Conference on
Real-Time Networks and Systems, Versailles, France,
page 23. ACM.
Bouaziz, R., Lemarchand, L., Singhoff, F., Zalila, B.,
and Jmaiel, M. (2015). Architecture exploration of
real-time systems based on multi-objective optimiza-
tion. In Proceedings of the 20nd International Confer-
ence on Engineering of Complex Computer Systems
(ICECCS), Gold Coast, QLD, pages 1–10. IEEE.
Burns, A. and Wellings, A. (2009). Real-Time Systems and
Programming Languages: Ada, Real-Time Java and
C/Real-Time POSIX. Addison-Wesley Educational
Publishers Inc, USA, 4nd edition.
Cottet, F. and Grolleau, E. (2005). Systmes Temps R
´
eel de
Contr
ˆ
ole-Commande. Dunod, Paris.
Gharsellaoui, H., Gharbi, A., Khalgui, M., and Ahmed, S.
(2012). Feasible automatic reconfigurations of real-
time os tasks. Handbook of Research on Industrial
Informatics and Manufacturing Intelligence: Innova-
tions and Solutions: Innovations and Solutions.
Klein, M., Ralya, T., Pollak, B., Obenza, R., and Harbour,
M. G. (1993). Analyzing complex systems. In Pro-
ceedings of Real-Time Analysis, US, pages 535–578.
Springer.
Krichen, F., Hamid, B., Zalila, B., and Coulette, B. (2010).
Designing dynamic reconfiguration for distributed
real time embedded systems. In Proceedings of
10th Annual International Conference on New Tech-
nologies of Distributed Systems (NOTERE), Tozeur,
Tunisia, pages 249–254. IEEE.
Lewine, D. (1991). POSIX programmers guide. O’Reilly
Media, Inc., USA.
Liu, C. and Layland, J. (1973). Scheduling algorithms for
multiprogramming in a hard-real-time environment.
Journal of the ACM (JACM), 20(1):46–61.
Mehiaoui, A., Wozniak, E., Tucci-Piergiovanni, S.,
Mraidha, C., Natale, M. D., Zeng, H., Babau, J.,
Lemarchand, L., and Gerard, S. (2013). A two-step
optimization technique for functions placement, par-
titioning, and priority assignment in distributed sys-
tems. ACM SIGPLAN Notices, 48(5):121–132.
Obenland, K. M. (2000). The use of posix in real-time sys-
tems, assessing its effectiveness and performance. The
MITRE Corporation.
Pagetti, C., Forget, J., Boniol, F., Cordovilla, M., and
Lesens, D. (2011). Multi-task implementation of
multi-periodic synchronous programs. Discrete event
dynamic systems, pages 307–338.
Pillai, P. and Shin, K. (2001). Real-time dynamic voltage
scaling for low-power embedded operating systems.
In Proceedings of the 13th Euromicro Conference on
Real-Time Systems, USA, pages 59–66. ACM.
Pillai, P. and Shin, K. (2012). Taste-an open-source tool-
chain for embedded system and software develop-
ment. In Proceedings of the Embedded Real Time
Software and Systems Conference (ERTS), Toulouse,
France.
Wo
´
zniak, E. Model-based Synthesis of Distributed Real-
time Automotive Architectures. PhD thesis, Universit
´
e
Paris Sud-Paris XI.
MILP-based Approach for Optimal Implementation of Reconfigurable Real-time Systems
335
