Efficient Randomized Regular Modular Exponentiation using Combined
Montgomery and Barrett Multiplications
Andrea Lesavourey
1
, Christophe Negre
1
and Thomas Plantard
2
1
DALI (UPVD) and LIRMM (Univ. of Montpellier, CNRS), Perpignan, France
2
CCISR, SCIT, University of Wollongong, Wollongong, Australia
Keywords:
RSA, Modular Exponentiation, Barrett, Montgomery, Differential Power Analysis, Correlation Power
Analysis, Randomization.
Abstract:
Cryptographic operations performed on an embedded device are vulnerable to side channel analysis and partic-
ularly to differential and correlation power analysis. The basic protection against such attacks is to randomize
the data all along the cryptographic computations. In this paper we present a modular multiplication algorithm
which can be used for randomization. We show that we can use it to randomize the modular exponentia-
tion of the RSA cryptosystem. The proposed randomization is free of computation and induces a level of
randomization from 2
10
to 2
15
for practical RSA modulus size.
1 INTRODUCTION
Modern digital communications are intensively en-
crypted and authenticated to ensure a good level of
confidentiality and security. Public key encryption
and signature is a concept initiated in 1976 by Diffie
and Hellman. This concept was realized by Rivest
Shamir and Adlemann who proposed the RSA cryp-
tosystem in (Rivest et al., 1978). This RSA cryptosys-
tem is nowadays the most used public key scheme for
electronic signature and remote authentication.
The basic operation in RSA protocols is an expo-
nentiation modulo a integer N which is of size 2048-
4096 bits. This exponentiation is generally com-
puted through a sequence of a few thousands squar-
ings and multiplications modulo N using the Square-
and-multiplication exponentiation scheme. Unfortu-
nately, a naive implementation of this algorithm on
an embedded device could be threaten by side chan-
nel analysis. These attacks monitor either power con-
sumption (Kocher et al., 1999), electromagnetic ema-
nation (Mangard, 2003) or computation time (Kocher,
1996) in order to extract the secret exponent.
The kind of attacks we will consider here are the
simple power analysis (SPA) (Kocher et al., 1999), the
differential and correlation power analysis (Kocher
et al., 1999; Brier et al., 2004). The SPA can be eas-
ily defeated by using a regular algorithm for the ex-
ponentiation like the Montgomery-ladder (Joye and
Yen, 2002) or the Square-and-multiply-always algo-
rithm (Coron, 1999). To counteract the differential
and correlation power analysis it is necessary to ran-
domize the data and the computations all along the
exponentiation.
In this paper we study a new method to randomize
modular exponentiation. This approach is based on
a modular multiplication algorithm which randomly
combines the two main methods for modular multi-
plication: Montgomery (Montgomery, 1985) and Bar-
rett multiplications (Barrett, 1987). The advantage of
this proposed randomization is that it is free of com-
putation. We then present a modified Montgomery-
ladder and a modified Square-and-multiply-always al-
gorithms for modular exponentiation which uses this
randomized modular multiplication. For these two
proposed randomized exponentiations we study the
level of randomization obtained.
The remainder of the paper is organized as fol-
lows. In Section 2 we review modular exponentiation
and side channel analysis. In Section 3 we review
the methods of Montgomery and Barrett for mod-
ular multiplication and we present a combined ver-
sion of these two methods. In Section 4 we study
two randomized exponentiations based on the com-
bined Montgomery and Barrett multiplication. Fi-
nally, in Section 5, we give some concluding remarks
and some perspectives.
368
Lesavourey, A., Negre, C. and Plantard, T.
Efficient Randomized Regular Modular Exponentiation using Combined Montgomery and Barrett Multiplications.
DOI: 10.5220/0005998503680375
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 368-375
ISBN: 978-989-758-196-0
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 EXPONENTIATION AND SIDE
CHANNEL ANALYSIS
The basic operation in RSA protocols is the modular
exponentiation: given an RSA modulus N, an expo-
nent E and X ∈ {0,... , N − 1} we have to compute
Y = X
E
mod N.
Generally, the most sensitive data is the exponent E.
This exponentiation can be efficiently computed with
the so-called Square-and-multiply algorithm which
consists in a sequence of squarings followed by a mul-
tiplication by X when the bit e
i
of E is equal to 1. This
approach is detailed in Algorithm 1.
Algorithm 1: Left-to-right Square-and-multiply.
Require: An RSA modulus N, an inte-
ger X ∈ {0,..., N − 1} and an exponent
E = (e
`−1
,.. . ,e
0
)
2
Ensure: R
0
= X
E
mod N
1: R
0
← 1
2: for i from `− 1 to 0 do
3: R
0
← R
2
0
mod N
4: if e
i
= 1 then
5: R
0
← R
0
× X mod N
6: end if
7: end for
8: return R
0
2.1 Side Channel Analysis of RSA
Exponentiation
When an RSA exponentiation is computed on an em-
bedded device it is under the threat of side-channel
analysis. Such attacks monitor either the power con-
sumption, the electromagnetic emanation or the com-
putation time in order to extract the secret data. We
review the simple power analysis (SPA) and differen-
tial/correlation power analysis (Kocher et al., 1999;
Brier et al., 2004):
• Simple Power Analysis. The simple power anal-
ysis (Kocher et al., 1999) threatens implementa-
tions based on the Square-and-multiply exponen-
tiation. Indeed, if the squaring of a data has a
different power trace than a multiplication, the
eavesdropper can read on the power trace the se-
quence of squarings and multiplications which
were computed. Then, since a multiplication is
done only when e
i
= 1, the attacker can easily de-
duce the sequence of bits of the exponent. Fig-
ure 1 illustrates this fact.
Counter-measures. SPA can be easily defeated by
using a regular algorithm for the computation of
Figure 1: SPA attack on the Square-and-multiply exponen-
tiation from (Kocher et al., 2011).
the exponentiation. For example the Square-and-
multiply-always approach proposed in (Coron,
1999) is a variant of the Square-and-multiply (Al-
gorithm 1) which performs a dummy multiplica-
tion when the bit e
i
= 0.
Another popular approach is the Montgomery-
ladder which is shown in Algorithm 2. This
approach is a variant of Algorithm 1 where a
second variable R
1
is used and always satisfies
R
1
= R
0
× X mod N. In the Montgomery-ladder,
when e
i
= 1, the two instructions R
0
← R
2
0
and
R
0
← R
0
× X are replaced by a single multiplica-
tion R
0
← R
0
×R
1
. Steps 5 and 8 are also included
to maintain the relation between R
0
and R
1
.
The power trace of the execution of the Square-
and-multiply-always and Montgomery-ladder al-
gorithms consists in a regular sequence of squar-
ings followed by a multiplication: this does not
leak anymore the bits of the exponent E.
Algorithm 2: Montgomery-ladder (Joye and Yen, 2002).
Require: An RSA modulus N, an integer X ∈
{0,.. . ,N − 1} and E = (e
`−1
,.. . ,e
0
)
2
Ensure: R
0
= X
E
mod N
1: R
0
← 1,R
1
← X
2: for i from 0 to ` − 1 do
3: if e
i
= 0 then
4: R
0
← R
2
0
mod N
5: R
1
← R
0
× R
1
mod N
6: else
7: R
0
← R
0
× R
1
mod N
8: R
1
← R
2
1
mod N
9: end if
10: end for
11: return R
0
• Differential and Correlation Power Analysis.
A more advanced attack called differential power
analysis was initiated in (Kocher et al., 1999).
This attack was later extended in (Brier et al.,
2004) as a correlation power analysis (CPA).
This attack extracts hidden information in the
power trace to identify the exact sequence of
operations. The principle is to follow the data
computed in the exponentiation algorithm: if we
know the first bits e
0
,e
1
,.. . ,e
i
and the message
Efficient Randomized Regular Modular Exponentiation using Combined Montgomery and Barrett Multiplications
369

X we can calculate X
i
= X
E
i
mod N where E
i
=
(e
i
,.. . ,e
0
)
2
. Next we guess the next bit e
i+1
= 0
or 1 and then compute the corresponding next
value X
i+1,0
= X
2
i
mod N or X
i+1,1
= X
2
i
× X
mod N in the next iteration. The power trace is
correlated to either X
i+1,0
or X
i+1,1
, so the authors
in (Kocher et al., 1999) use a differential of multi-
ple power traces to accurately decide which value
of e
i+1
is the correct guess. The authors in (Brier
et al., 2004) evaluate the covariance between the
Hamming weight of data X
i+1,0
or X
i+1,1
and the
power traces to decide which guess is correct.
Counter-measures. The basic approach to coun-
teract differential and correlation power analysis
is to inject randomization in the exponentiation.
Specifically, the three main strategies to random-
ize the data are the following:
– Exponent blinding: this strategy given
in (Coron, 1999) add to E a random multiple
of φ(N) = (p −1)(q − 1)
E
0
= E +β × φ(N)
Then exponentiation X
E
0
mod N = X
E
mod N is the same. This leads to unpredictable
values taken by R
0
during the exponentiation.
– Message blinding: The idea is to mask X and
thus makes it impossible to predict anything
regarding the power trace related to X. We
choose a random value ρ for which we know
ρ
E
0
and we compute
X
0
= X ×ρ
E
0
mod N
Then we compute X
0E
mod N = X
E
× ρ
E
0
E
mod N = X
E
× ρ mod N and then we divide
by ρ to get X
E
mod N.
– Randomization of modular multiplication: the
main approach is the use of randomized expres-
sion modulo N, instead of X we use X
0
≡ X
mod N with X
0
∈ {0,.. . ,2
w
N}. The value X
0
can then be randomly generated as follows:
X
0
← X
0
+ βN,
with β random in {0,.. ., 2
w
}. The drawback of
this approach is that each modular multiplica-
tion becomes more expensive, resulting in a
penalty in space requirement, computation time
and power consumption.
In the sequel we will present an alternative ap-
proach for the randomization in modular exponentia-
tion in order to get a cheaper counter-measure against
differential and correlation power analysis.
3 MODULAR MULTIPLICATION
In this section we first review the two main methods,
Montgomery (Montgomery, 1985) and Barrett (Bar-
rett, 1987), for the computation of a multiplication
modulo an integer N as the ones used in RSA cryp-
tosystems. These methods differ in the way the prod-
uct is reduced: the Montgomery method reduces the
product by clearing the least significant bits and the
method of Barrett reduces the product by clearing the
most significant bits. We will then present a combi-
nation of these two approaches which can be used to
randomize a multiplication modulo N.
3.1 Montgomery Multiplication
Let N be an n-bit modulus which is stored on t com-
puter words with t = dn/we and each computer word
containing w bits. Let X be a t-word integer in [0, N]
and Y be an s-word integer such that s ≤ t. Usually
we have s = t when we want to compute the product
of two elements modulo N. But in the sequel we will
need this version of the Montgomery multiplication
with a multiplicand of word size s < t.
The word level form of Montgomery multiplica-
tion computes R = X ×Y × 2
−sw
mod N as follows:
it sequentially multiply X by the s words of Y and add
it to Z, and reduce Z by clearing its w least signifi-
cant bits. For each word reduction: it computes Q of
bit length w such that Z + Q × N have its w least sig-
nificant bits equal to 0, it finally computes the exact
division (Z + Q × N)/2
w
which is equal to Z × 2
−w
mod N. The main advantage of the Montgomery ap-
proach for modular multiplication is that it avoids a
costly integer divisions. This approach is shown in
Algorithm 3.
Algorithm 3: MontMul.
Require: 2
n−1
< N < 2
n
the modulus of bit-length
n, X = (X
t−1
,.. . ,X
0
)
2
w
an integer in [0,N] and
Y = (Y
s−1
,.. . ,Y
0
)
2
w
an integer in [0, ...,2
ws
[ and
N
0
= −N
−1
mod 2
w
Ensure: R = X ×Y × 2
−sw
mod N
1: for i = 0 to s −1 do
2: Z ← Z +X ×Y
i
3: Q ← N
0
× Z mod 2
w
4: R ← (Z + Q ×N)/2
w
5: end for
6: if R ≥ N then
7: R ← R −N
8: end if
9: return R
SECRYPT 2016 - International Conference on Security and Cryptography
370

3.2 Barrett Multiplication
We consider a modulus N of bit length n and word
length t. Let X be an integer of word length t and Y
be an integer of word length s ≤ t. Usually we have
s = t but in the sequel we will need this version of
Barrett multiplication with s < t.
The approach of Barrett to perform the modular
multiplication (X ×Y ) mod N is the following: it se-
quentially multiply X the words of Y , add the result
to Z, and reduce Z modulo N by clearing the most
significant bits. For each word reduction it approxi-
mates the quotient Q of the division of Z by N and
then computes the remainder R = Z − QN. This ap-
proach is shown in Algorithm 4.
ˆ
Q in Algorithm 4 is
Algorithm 4: BarrettMul.
Require: N a modulus of bit length n and word
length t, X = (X
t−1
,.. . ,X
0
)
2
w
an integer in [0, N]
and Y = (Y
s−1
,.. . ,Y
0
)
2
w
an integer in [0, ...,2
s
[
and N
0
= b2
n+w+3
/Nc
Ensure: R = X ×Y mod N
1: for i = s −1 to 0 do
2: Z ← Z ×2
w
+ X ×Y
i
3:
ˆ
Q ← bbZ/2
n−2
cN
0
/2
w+5
c
4: R ← Z −
ˆ
QN
5: end for
6: if R ≥ N then
7: R ← R −N
8: end if
9: return R
a good approximation of the quotient Q = b
Z
N
c. The
authors of (Knezevic et al., 2009) showed that
Q ≥
ˆ
Q ≥ Q −1.
This means that Step 7 in Algorithm 4 returns the cor-
rect element R = X ×Y mod N.
3.3 Combined Montgomery and Barrett
Multiplication
Now, we present our first contribution. We consider
two n-bit integers X and Y stored on t = dn/we words.
We combine Montgomery and Barrett multiplication
in order to compute
R = X ×Y × 2
−sw
mod N
with an arbitrary s ∈ [0,t]. For this, we split the integer
X into two parts X = X
0
+ 2
sw
X
1
. We then perform
Z
0
= MontMul(Y,X
0
) = Y × X
0
× 2
−sw
mod N,
Z
1
= BarrettMul(Y,X
1
) = Y × X
1
mod N.
We then obtain the required result R = X ×Y × 2
−sw
mod N as follows
Z
0
+ Z
1
=Y × X
0
× 2
−sw
+Y × X
1
mod N
=Y × (X
0
+ 2
s
X
1
)2
−sw
mod N
=X ×Y × 2
−sw
mod N.
Algorithm 5 gives the details of this approach.
Algorithm 5: CombMontBarrettMul.
Require: 2
n−1
< N < 2
n
the modulus of bit-length n
and word length t, X = (X
t−1
,.. . ,X
0
)
2
w
and Y =
Y
n−1
,.. . ,Y
0
)
2
w
two integers in [0, N[ and a split
s ∈ [0,t]
Ensure: Z = X ×Y × 2
−sw
mod N
1: Split. X = X
0
+ 2
sw
X
1
2: Z
0
← MontMul(Y, X
0
)
3: Z
1
← BarrettMul(Y, X
1
)
4: Z ← Z
0
+ Z
1
5: if Z > N then
6: Z ← Z −N
7: end if
8: return Z
3.4 Complexity Comparison
We use the word level Montgomery and Barrett algo-
rithms reviewed in Subsection 3.1 and 3.2. We study
the complexity in terms of word additions (Add) and
word multiplications (Mul). The complexity of Bar-
ret and Montgomery multiplications (without the final
subtraction by N) for a t-word X and an s-word Y are
as follows
• Barret: #Mul = s(t + 1) and #Add = s(3t + 2).
• Montgomery: #Mul = s(t +1) and #Add = s(3t +
2).
This leads to the following complexity of the Com-
binedMontMul algorithm (including the final subtrac-
tion by N):
#Mul = s(t +1) + (t − s)(t + 1) = t
2
+t
#Add = s(3t + 2) + (t −s)(3t + 2) +t
= 3t
2
+ 3t + t
This leads to the complexity shown in Table 1 for
the multiplication of the t words integers X and Y
with the three approaches: Montgomery, Barrett and
combined Montgomery Barrett. These complexity in-
cludes the final subtraction to get Z < N.
Since the complexity of the word level form of
CombMontBarretMul is the same as Montgomery
and Barrett, we can take advantage of the algorithm
to randomize modular exponentiation. We will study
this strategy in the following section.
Efficient Randomized Regular Modular Exponentiation using Combined Montgomery and Barrett Multiplications
371

Table 1: Complexity comparison of Montgomery, Barrett
and combined Montgomery Barrett.
#Add #Mul Total
Montgomery t
2
+t 3t
2
+ 2t + t 4t
2
+ 3t
Barrett t
2
+t 3t
2
+ 2t + t 4t
2
+ 3t
Combined
Montgomery
and Barret
t
2
+t 3t
2
+t 4t
2
+ 3t
4 RANDOMIZED
EXPONENTIATION
We present in this section two randomized exponenti-
ations which uses CombMontBarretMul for modular
multiplications.
4.1 Randomized Montgomery-ladder
We first consider the Montgomery-ladder (Algo-
rithm 2). We randomize this exponentiation by us-
ing CombMontBarrettMul for each modular multipli-
cation. Before each multiplication the splitting s for
CombMontBarretMul is randomly generated. The ef-
fect is that in the Montgomery-ladder exponentiation
we have
f
R
0
= R
0
2
γw
mod N and
f
R
1
= R
1
2
γw
mod N
such that the integer γ evolves randomly. The integer
s is randomly chosen in order to keep γ in the interval
[t/3,2t/3]. This approach is shown in Algorithm 6.
Algorithm 6: Randomized-Montgomery-ladder.
Require: An RSA modulus N of bit length n, an in-
teger X ∈ {0, .. .,N − 1} and E = (e
`−1
,.. . ,e
0
)
2
Ensure: R
0
= X
E
mod N
1: s
`
← rand(t/3,2t/3)
2: γ
`
← s
`
w
3:
e
R
0
← 2
s
`
w
4:
e
R
1
← BarrettMul(X,2
s
`
w
)
5: for i from `− 1 to 0 do
6: γ
i
← rand(t/3,2t/3)
7: s
i
← 2γ
i+1
− γ
i
8: if e
i
= 1 then
9:
e
R
0
← CombMontBarrettMul(
e
R
0
,
e
R
1
,s
i
)
10:
e
R
1
← CombMontBarrettMul(
e
R
1
,
e
R
1
,s
i
)
11: else
12:
e
R
1
← CombMontBarrettMul(
e
R
0
,
e
R
1
,s
i
)
13:
e
R
0
← CombMontBarrettMul(
e
R
0
,
e
R
0
,s
i
)
14: end if
15: end for
16:
e
R
0
← CombMontBarrettMul(R
0
,1,γ
0
)
17: return
e
R
0
Validity of Algorithm 6. Let
e
R
(i)
0
and
e
R
(i)
1
be the val-
ues of
e
R
0
and
e
R
1
after the i-th iteration. The integer γ
i
in Algorithm 6 satisfies
e
R
(i)
0
= R
0
× 2
γ
i
w
mod N and
e
R
(i)
1
= R
(i)
1
× 2
γ
i
w
mod N where R
(i)
0
and R
(i)
1
are the
values of R
0
and R
1
after the i-th loop of the non-
randomized Montgomery-ladder exponentiation (i.e.
Algorithm 2). When e
i
= 1 we have
e
R
(i)
0
= (R
(i+1)
0
× 2
γ
i+1
w
)
×(R
(i+1)
1
× 2
γ
i+1
w
) × 2
−s
i
w
mod N
= R
(i+1)
0
× R
(i+1)
1
× 2
2γ
i+1
w−s
i
w
mod N
= R
(i)
0
× 2
2γ
i+1
w−s
i
w
mod N
which means that the instruction s
i
= 2γ
i+1
− γ
i
in
Step 7 is correct. Let us now check that s
i
is al-
ways in [0,t]. We have γ
i+1
,γ
i
∈ [t/3,2t/3] then
2t/3 ≤ 2γ
i+1
≤ 4t/3 and then
0 ≤ 2γ
i+1
− γ
i
≤ 3t/3
which implies that s
i
= 2γ
i+1
− γ
i
is in [0,t].
The main advantage of the proposed randomiza-
tion is that it is free of computation. But its main
drawback is that the level of randomization is not so
important since we have, at each loop iteration, only
t/3 possible values for
e
R
0
and
e
R
1
. In practice this
means that we have to combine the proposed random-
ization with the classical ones reviewed in Section 2.
When these strategies are combined to the one pro-
posed here we can obtain any level of randomization
with a reduced cost.
4.2 Randomized Right-to-left
Square-and-multiply-always
Now, we extend the randomization technique pre-
sented in Subsection 4.1, to the Right-to-left Square-
and-multiply-always exponentiation. This algorithm
is reviewed in Algorithm 7. Our goal is to get a regu-
lar exponentiation with a large level of randomization.
We propose to randomize Algorithm 7 as follows:
• We randomize Z with the strategy of Subsec-
tion 4.1. We have
e
Z
i
= Z
(i)
× 2
γ
i
w
mod N such
that γ
i
is in [t/3,2t/3] all along the exponentia-
tion.
• We randomize R
0
and R
1
as follows: before each
multiplication R
0
×Z mod N and R
1
×Z mod N
we randomly choose s
0
i
∈ [0,t]. Then we per-
form the multiplications R
0
×Z mod N or R
1
×Z
mod N with CombMontBarrettMul with split s
0
i
.
This randomized version of Algorithm 7 is shown
in Algorithm 8.
Validity of Algorithm 8. The way γ and
e
Z
evolve in Algorithm 8 is well known since it
SECRYPT 2016 - International Conference on Security and Cryptography
372

Algorithm 7: Right-to-left Square-and-multiply-always.
Require: An RSA modulus N of bit length n, an in-
teger X ∈ {0, .. .,N − 1} and E = (e
`−1
,.. . ,e
0
)
2
Ensure: R
0
= X
E
mod N
1: R
0
← 1
2: R
1
← 1
3: Z ← X
4: for i from 0 to ` − 1 do
5: if e
i
= 0 then
6: R
0
← R
0
× Z mod N
7: else
8: R
1
← R
1
× Z mod N
9: end if
10: Z ← Z
2
mod N
11: end for
12: return R
1
Algorithm 8: Randomized Right-to-left Square-and-
multiply-always.
Require: An RSA modulus N of bit length n, an in-
teger X ∈ {0, .. .,N − 1} and E = (e
`−1
,.. . ,e
0
)
2
Ensure: R
0
= X
E
mod N
1: s
−1
← rand(t/3,2t/3)
2:
e
R
0
← 1,
e
R
1
← 1,
e
Z ← Barrett(X,2
s
−1
w
)
3: γ
−1
← s
−1
,γ
0
−1
← 0
4: for i from 0 to ` − 1 do
5: s
0
i
← rand(0,t)
6: if e
i
= 0 then
7:
f
R
0
← CombMontBarrettMul(
f
R
0
,
e
Z,s
0
i
)
8: γ
0
i
← γ
0
i−1
+ (γ
i−1
− s
0
i
)
9: else
10:
f
R
1
← CombMontBarrettMul(
f
R
1
,
e
Z,s
0
i
)
11: γ
0
i
← γ
0
i−1
12: end if
13: γ
i
← rand(t/3,2t/3)
14: s
i
← 2γ
i−1
− γ
i
15:
e
Z ← CombMontBarrettMul(
e
Z,
e
Z,s)
16: end for
17: return
e
R
1
was studied in Subsection 4.1. Consequently, we have
e
Z
(i)
= Z
(i)
× 2
γ
i
w
mod N where Z
(i)
is the value of Z
after the i-th loop in the non-randomized Algorithm 7
and γ
i
is a random element in [t/3,2t/3].
Now we consider
e
R
(i)
1
and γ
0
i
. We have:
e
R
(i)
1
= R
(i)
1
× 2
γ
0
i
w
mod N.
The value γ
0
i+1
is expressed in terms of γ
0
i
,γ
i
and s
0
i+1
as follows:
• If e
i+1
= 1 we have
e
R
(i+1)
1
=
e
R
(i)
1
×
e
Z × 2
−s
0
i+1
w
mod N
=R
(i)
1
× 2
γ
0
i
w
× Z × 2
γ
i−1
w
×2
−s
0
i+1
w
mod N
=R
(i+1)
1
× 2
γ
0
i
w+γ
i
w−s
0
i+1
w
mod N
which means that γ
0
i+1
= γ
0
i
+ γ
i
− s
0
i+1
.
• If e
i+1
= 0 we have
e
R
(i+1)
1
=
e
R
(i)
1
= R
(i+1)
1
× 2
γ
0
i
mod N
which gives γ
0
i+1
= γ
0
i
.
So if we set
δ
i+1
=

γ
i
− s
0
i+1
if e
i+1
= 1
0 if e
i+1
= 0
we have γ
0
i+1
= γ
0
i
+δ
i+1
, which means that γ
0
i
consists
in random walk of step sizes δ
i
for i = 1, ...,` − 1.
The absolute value of these step sizes δ
i
are bounded
by 2t/3: indeed since s
0
i
always satisfies 0 ≤ s
0
i
≤ t we
always have
−2t/3 = t/3 −t ≤ γ
i−1
− s
0
i
| {z }
δ
i
≤ 2t/3 − 0 = 2t/3.
Such random walk can get away from 0 as i in-
creases. This is interesting since this enlarges the pos-
sible values for
e
R
1
, i.e., this enlarges the level of ran-
domization.
But, on the other hand, this random walk induces
a problem we need to tackle: the final value γ
0
`−1
can
be a quite large integer and this might render difficult
to extract R
(`)
1
from
e
R
(`)
1
.
We propose a strategy which controls the way γ
0
i
evolves, in order to have the final value γ
0
`−1
= 0. The
following lemma provides the conditions to reach this
goal.
Lemma 1. Let E be an `-bit exponent and let h
E
be
his hamming weight. We denote {i
0
,.. . ,i
h
E
} the set
of indexes i such that e
i
6= 0. In Algorithm 8 we can
choose the integers s
0
i
such that:
δ
i
> 0 for the first h
E
/2 bits e
i
6= 0,
δ
i
< 0 for the last h
E
/2 bits e
i
6= 0,
and such that we have
0 ≤ γ
0
i
j
< (h
E
− j)2t/3 for j = 1,... , h
E
for all i
j
∈ {i
0
,.. . ,i
h
E
}.
Proof. There are the following two phases in the evo-
lution of γ
i
:
Efficient Randomized Regular Modular Exponentiation using Combined Montgomery and Barrett Multiplications
373

• Ascending phase. This phase corresponds to
loops i
j
for j = 1,. .. ,h
E
/2 where chose s
0
i
j
such
that δ
i
j
∈ [0,2t/3]. Consequently, after loop i
j
we
have made j such step sizes and then the exponent
of
e
R
(i
j
)
1
satisfies:
0 ≤ γ
0
i
j
≤ j2t/3 ≤ (h
E
− j)2t/3.
• Descending phase. This phase corresponds to
loops i
j
for j = h
E
/2 + 1,... ,h
E
. If we have γ
0
i
j
≤
(h
E
− j)2t/3 then there exists a step size δ
i
j
∈
[−2t/3,0] which yields γ
0
i
j+1
< (h
E
− j)2t/3 −
t/3. Such δ
i
j
can be obtained by choosing prop-
erly s
0
i
j
and γ
i
j
−1
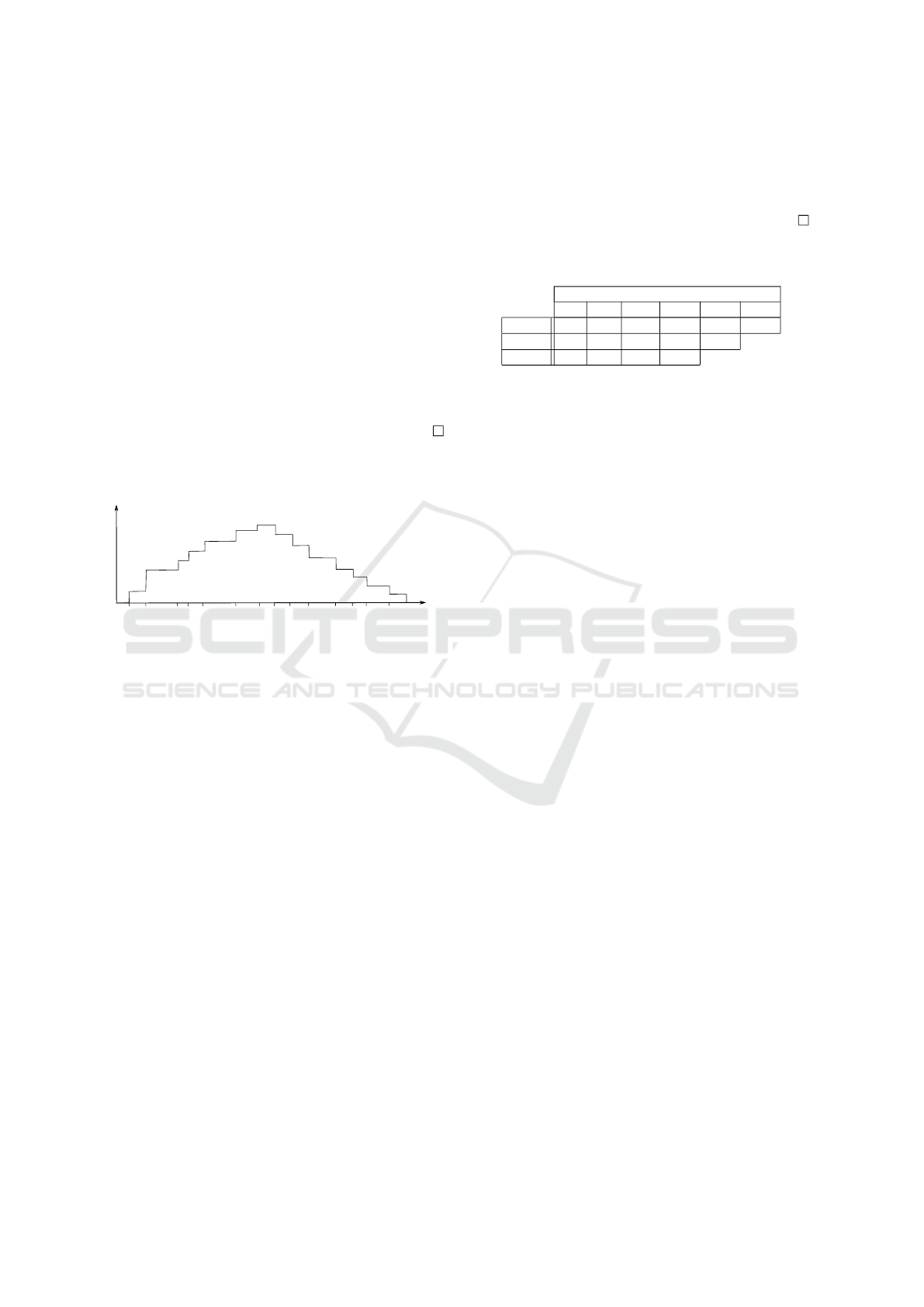
Figure 2 illustrates the way γ
0
i
increase and then
decrease towards 0.
i
1
i
2
i
3
i
4
i
5
i
6
i
7
i
8
i
9
i
10
i
11
i
12
i
13
i
14
iteration
random
exponent
Figure 2: Evolution of the exponent γ based on Lemma 1.
Level of Randomization. We now focus on the level
of randomization injected in
e
R
(i)
1
in Algorithm 8 un-
der the restriction of Lemma 1. The number of possi-
ble values for
e
R
(i)
1
depends on i and on the Hamming
weight of E. The following lemma establishes the av-
erage case of this level of randomization.
Lemma 2. Let
e
R
(i)
1
= R
(i)
1
2
γ
0
i
mod N be the value of
e
R
1
at the end of the i-th loop in Algorithm 8. Then γ
0
i
satisfies the following:
i) For i < `/2 we have, in average, γ
0
i
∈ [0, (2t/3) ×
(i/2)]
ii) For i > `/2 we have, in average, γ
0
i
∈ [0, (2t/3) ×
(` − i)/2]
Proof. We prove each case i) and ii) separately:
i) Let α
i
be the number of e
j
6= 0 with j ≤ i. Then
the maximal value for γ
0
i
which can be reached at
loop i is (2t/3)× α
i
which corresponds to a walk
of α
i
steps of size 2t/3. In average, we have α
i
=
i/2 such non-zero e
j
with j ≤ i and this leads to
the assertion i) of the lemma.
ii) For i > `/2 we consider that we make backward
steps starting from the end where we start at
γ
0
`
= 0. We make ` −i steps backwards, and only
(` − i)/2 of them have step size 6= 0, the maxi-
mal distance walked is (2t/3)×(`−i)/2 and this
leads to assertion ii) of the lemma.
Table 2: Level of randomization for practical sizes of N,
w = 32 and several loop iterations.
Loop iterations i
50 100 500 1000 1500 2000
RSA 4096 2
10
2
11
2
13.4
2
14.4
2
15
2
15.4
RSA 3072 2
10
2
11
2
13.4
2
14.4
2
15
RSA 2048 2
10
2
11
2
13.4
2
14.4
The previous lemma shows that the level of ran-
domization for
e
R
(i)
1
becomes large as soon as we ad-
vance in the exponentiation. Table 2 shows the level
of randomization obtained for different size of RSA
modulus and different values for i.
5 CONCLUSION
In this paper we focused on counter-measures based
on randomization of RSA exponentiation against side
channel analysis. We proposed to perform modular
multiplications with a combination of Montgomery
and Barrett multiplications. This algorithm provides
a way to randomize modular multiplication by setting
the splitting value s at random. We then provided
a modified version of two regular algorithm, i.e.,
Montgomery-ladder and Square-and-multiply-always
exponentiation. We analyzed the algorithms which
showed that the proposed approach for randomization
is interesting since it does not induce any penalty in
terms of performance.
REFERENCES
Barrett, P. (1987). Implementing the Rivest Shamir and
Adleman Public Key Encryption Algorithm on a Stan-
dard Digital Signal Processor. In CRYPTO ’86, pages
311–323. Springer-Verlag.
Brier, E., Clavier, C., and Olivier, F. (2004). Correlation
Power Analysis with a Leakage Model. In CHES
2004, volume 3156 of LNCS, pages 16–29. Springer.
Coron, J.-S. (1999). Resistance against Differential Power
Analysis for Elliptic Curve Cryptosystems. In CHES,
pages 292–302.
Diffie, W. and Hellman, M. (1976). New directions
in cryptography. IEEE Trans. Information Theory,
22(6):644–654.
Joye, M. and Yen, S. (2002). The Montgomery Powering
Ladder. In CHES 2002, volume 2523 of LNCS, pages
291–302. Springer.
SECRYPT 2016 - International Conference on Security and Cryptography
374

Knezevic, M., Vercauteren, F., and Verbauwhede, I. (2009).
Speeding Up Barrett and Montgomery Modular Mul-
tiplications.
Kocher, P. (1996). Timing Attacks on Implementations of
Diffie-Hellman, RSA, DSS, and Other Systems. In
Advances in Cryptology - CRYPTO ’96, volume 1109
of LNCS, pages 104–113. Springer.
Kocher, P., Jaffe, J., Jun, B., and Rohatgi, P. (2011). In-
troduction to differential power analysis. J. Crypto-
graphic Engineering, 1(1):5–27.
Kocher, P. C., Jaffe, J., and Jun, B. (1999). Differen-
tial Power Analysis. In Advances in Cryptology,
CRYPTO’99, volume 1666 of LNCS, pages 388–397.
Springer.
Mangard, S. (2003). Exploiting Radiated Emissions - EM
Attacks on Cryptographic ICs. In Austrochip 2003,
Linz, Austria, October 1st, pages 13–16.
Montgomery, P. (1985). Modular Multiplication Without
Trial Division. Math. Computation, 44:519–521.
Rivest, R., Shamir, A., and Adleman, L. (1978). A method
for obtaining digital signatures and public-key cryp-
tosystems. Communications of the ACM, 21:120–126.
Efficient Randomized Regular Modular Exponentiation using Combined Montgomery and Barrett Multiplications
375