Dynamic and Acoustic Properties of a Joisted Floor

Edoardo Alessio Piana, Candida Petrogalli and Luigi Solazzi

Department of Mechanical and Industrial Engineering, University of Brescia, via Branze 38, Brescia, Italy

Keywords: Point Mobility, Bending Stiffness, Sound Reduction Index.

Abstract: Lightweight structures find more and more applications in both vehicle and ship industries. To meet a growing

demand, a variety of different types of joisted panels have been developed during the last few decades. One

of the problems to deal with is the assessment of the acoustic performances of such panels once they are

already mounted in their final place. In this case, it can be of importance to find a way to characterise their

dynamic and acoustic properties, such as bending stiffness, internal losses and sound reduction index through

non-destructive testing. A method for a quick determination of the bending stiffness of a lightweight joisted

floor is presented. On the basis of the apparent bending stiffness and of the losses, it is possible to predict the

sound reduction index of the panel in a fairly simple way. The results obtained from the mobility tests have

been compared to the measurements carried out according to the ISO standard procedure.

1 INTRODUCTION

The expression “joisted floor” refers to a structure

with a multi-layer plate bonded to joists placed at one

side of the floor. This type of floor combines low

weight with high strength. However the acoustic

properties can be very poor, thus severely restricting

the use of such lightweight elements. It is therefore

essential to optimize the acoustic performances

through predictions. In case of sandwich-like

structures, some of the basic dynamic and acoustic

parameters can be determined by means of simple

tests using a beam element cut from the assembly

(Nilsson and Nilsson, 2002) and (Nilsson and Liu,

2016). Some frequency response measurements can

determine a number of natural frequencies of the

beam. Based on these results the apparent bending

stiffness can easily be determined through least

square method applied to the experimental points.

The apparent bending stiffness of a composite

structure at one natural frequency is equal to the

bending stiffness of a simple Euler beam having the

same length, boundary conditions and weight as the

considered sandwich structure at the same frequency.

Obviously, it is not always possible to cut beams from

an already mounted structure. (Roelens et al., 1997)

and (Nightingale et al., 2004) have tested different

measurement techniques on building components for

the determination of their stiffness properties in situ.

Although these methods seem to be quite complicated

and a number of them cannot be adopted for some

types of building components.

In the following sections, a method is presented

through which the material parameters can be

determined from simple point mobility measurements

on a plate element. In particular, this method has been

applied to a kind of panel which cannot be strictly

defined as sandwich, since it is made up of several

layers and some thick joists attached to one side of the

assembly. It will be shown that the point mobility

technique allows to estimate the apparent bending

stiffness also in this case, thus taking into account the

real boundary conditions of the mounted structure.

The sound reduction index results obtained from

point mobility measurements will be compared to

those found after the tests carried out according to the

existing ISO standards.

2 BENDING STIFFNESS

DERIVED FROM POINT

MOBILITY MEASUREMENTS

If an harmonic force F = F

exp(iωt) is injected at a

specific point of a system, it will move with a certain

velocity v. In the point where the excitation is given,

a point mobility function Y can be defined as the ratio

between the Fourier transform of the velocity signal

and the Fourier transform of the force signal

measured at the same position:

Piana, E., Petrogalli, C. and Solazzi, L.

Dynamic and Acoustic Properties of a Joisted Floor.

DOI: 10.5220/0005994202770282

In Proceedings of the 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2016), pages 277-282

ISBN: 978-989-758-199-1

277

  



FvY



(1)

The behaviour of a finite vibrating structure can be

predicted from that of infinite ones. The bending

waves induced by a point force in an infinite plate can

spread indefinitely in any direction. If a finite plate is

considered, the bending waves reach the borders of

the plate, and then are reflected back. If a force is

acting at a specific point of the plate, the resulting

velocity will be mainly determined by the plate

dimensions, mass per unit area, bending stiffness and

boundary conditions, thus the point mobility will

depend on position and frequency. However, an

averaging of the real part of the point mobility carried

out over space and frequency for a finite structure is

in the mid- and high-frequency region identical to the

real part of the point mobility of an infinite structure

made of the same material and having the same

thickness:

 









 YY ReRe

(2)

Consequently, the power input, introduced into a

panel having finite dimensions by a force acting

randomly in time and space, can be determined as if

the panel had infinite dimensions and were excited by

a point force having a power spectral density

equivalent to the sum of the power spectral densities

of all the point sources operating on the finite

structure. This statement is valid because in the mid-

high frequency range the modal density is significant,

thus making the mobility independent of the structure

extension. This means that the theory cannot be

applied without taking into account corrections for

the first few modes in the low frequency range. It has

been be shown (Fahy and Mohammed, 1992) that, in

order to extend this consideration to the low

frequency range, at least 5 modes have to be included

within each frequency band of interest to have a fair

accuracy. As concerns the space average, the mobility

has to be measured over a large number of points, and

the points have to be randomly distributed over the

panel surface, in order to obtain a good representation

of the dynamic properties of the panel. If these

conditions are fulfilled, the mobility of a finite panel

can be determined using the formulation of the

mobility for an equivalent infinite structure (Nilsson

and Liu, 2016). In this case, the frequency average of

the mobility can be written as:

''8



Y 

(3)

where D

and μ'' are the bending stiffness per unit

width and the mass per unit area of the panel,

respectively. The bending stiffness per unit width of

the panel at the central frequency of each frequency

band is obtained as:



Re''64





(4)

For modes (m,n) having m = 0 or n = 0, it can be

shown that (Nilsson and Liu, 2016):

''4



Y 

(5)

Therefore, for the first natural frequencies

corresponding to such mode types, the measured

bending stiffness should be multiplied by a factor 4.

The influence of the mass of the accelerometer

used during the mobility measurements has to be

taken into account, especially for lightweight

structures. As discussed in (Nilsson and Liu, 2016),

the dynamic response of the structure and its modal

behaviour, can be influenced by the added mass of the

transducer Δμ. The measured point mobility should

then be modified according to the correlation:









iYYY

measured







(6)

In the low frequency region the effect of the mass Δμ

is negligible. For higher frequencies, the denominator

increases and the magnitude of the measured point

mobility can decrease significantly.

This aspect must be taken into account in case of

lightweight structures when the mobility is measured

by using an impact hammer and an accelerometer,

while an impedance head is less sensitive.

2.1 Sound Reduction Index

The response of a structure excited by an external

sound field can be predicted fairly accurately once the

apparent bending stiffness of the structure is known

(Backström and Nilsson, 2007).

The derivation of the sound reduction index for

homogeneous panels as a function of the bending

stiffness of the plate and other parameters is discussed

in (Cremer, 1942). The expressions can be used for

sandwich structures once some adjustments are made.

For this reason it is useful to introduce the critical

frequency f

. This particular parameter is the

frequency for which the wavenumber in air is equal

to the wavenumber of the flexural waves on the plate.

The frequency f

is given by









μ"/Dπ/c =/kkπc/f

pairplatec

 22

(7)

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

278

where c is the speed of sound in air. For a thin

homogeneous panel, the bending stiffness D

is not

frequency dependent and f

is a constant.

The transmission coefficient τ(φ) at the angle of

incidence φ is given by



1sincos

sincos





























































































































(8)

where ρc is the impedance of air, equal to

415 kg/(m

s) and f

is the critical frequency satisfying

equation 7. As previously stated, for a single leaf

panel D

is constant. However, for a multylayered

structure the bending stiffness is frequency

dependent. The sound reduction index of a sandwich

structure can be derived by replacing f

in equation 8

with a the parameter f'













(9)

The sound reduction index R is defined as

10∙log(1/τ

), where τ

is the sound transmission

coefficient for diffuse incidence:











sincos2

(10)

The sound reduction index for the plates described

hereafter was predicted according to equations 8-10

and compared to measurements carried out according

to the procedures described in the international

standards.

2.2 Specimen under Test

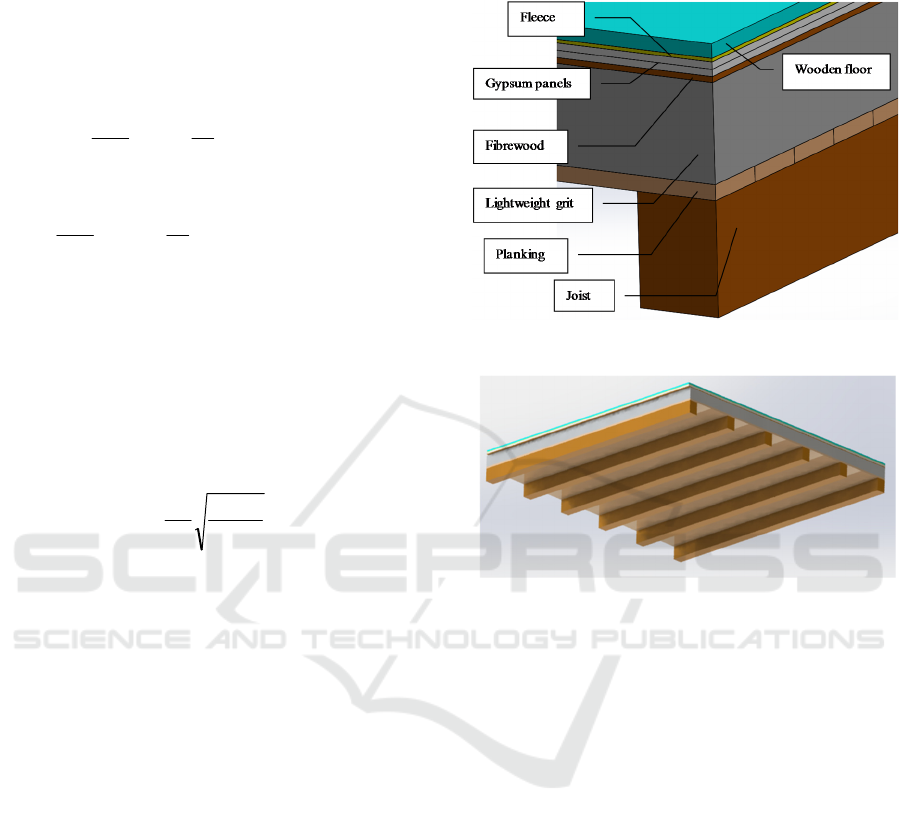
The investigated specimen is made of two main parts:

a floor, made of different layers, and the joists (Figure

1).

Starting from the upper layer, the thicknesses are:

20 mm, 5 mm, 2 x 10mm, 8 mm, 140 mm, 22 mm.

The joists are 120 mm x 160 mm wooden studs. The

overall thickness of the floor is 215 mm.

The dimensions of the surface are

3.31 m x 3.38 m. Figure 2 shows a layout of the floor,

together with the spacing between the ribs. The lower

wooden layer and the studs are kept together by a thin

layer of glue.

The overall mass per unit area of the floor is

85.08 kg/m

Figure 1: Layers of the joisted floor.

Figure 2: Layout of the ribs and main dimensions of the

panel.

3 TEST METHODS AND

MATERIALS

The floor is mounted between the ground floor and

the second floor of a small building (Figure 3).

The lateral sides of the floor are sealed by placing

a resilient mat plus high density foam to fill all the

gaps between the wooden frame and the wall.

On the joisted side, 20 point mobility

measurement positions were spread on the surface: 10

positions on the joists and 10 positions in between

them.

A PCB Piezotronics accelerometer type 352C33 was

attached to the floor and then the floor was his as

close as possible to it by means of an impedance

hammer PCB Piezotronics type 086C03, equipped

with a nylon tip. The velocity and force signals

coming from the transducers were acquired by an

OROS 36 multi-channel system able to compute

directly the real and imaginary parts of the mobility

Dynamic and Acoustic Properties of a Joisted Floor

279

function. The frequency span of the acquisition was

selected from 0 to 6.4 kHz, 1 Hz resolution.

Figure 3: Pictures of the floor used for the tests and of the

building where it is mounted.

3.1 Point Mobility Measurements

The point mobility measurements were performed

directly in situ.

Figure 4: Measurement positions for point mobility.

Figure 4 shows how the measurement positions

are distributed across the panel surface.

The post processing of the data was carried out by

exporting the text data from the OROS NVGate

software. Importing the real part of the mobility in an

ad-hoc software, it was possible to compute the

average mobility for the 20 measurement positions.

Finally, the mobility value was computed

synthesising the values into 1/3 octave bands,

extended to have at least 5 modes inside the frequency

span defined by each band. Once the average mobility

is known, it is possible to compute the related bending

stiffness and to use this value to determine the

apparent bending stiffness through the least square

method applied to a set of points f

, D

and to the

following equation

2/12/3

 CDD

xxx

(11)

which describes the general behaviour of the apparent

bending stiffness D

for a sandwich panel (Nilsson

and Nilsson, 2002). As shown in (Piana, 2016), the

general form of equation 11 can be used to describe

the bending stiffness of different types of orthotropic

panels, including ribbed structures.

Since the modal density in the low frequency

range is low, there is some lack of points for

computing the bending stiffness. For this reason a

fictitious bending stiffness point D

has been

introduced in order to “guide” the curve in the very

low frequency region. The static bending stiffness D

can be computed once some geometrical and material

parameters are known using the following equation:

lcl

hhE

D 

(12)

where E

is the Young’s modulus for one laminate, h

is the core thickness and h

is the thickness of one

laminate.

4 RESULTS

4.1 Determination of the Loss Factor

Before starting with the computation of the sound

reduction index of the panels, it is necessary to

determine the losses. The determination of the losses

was made through the evaluation of the structural

reverberation time.

Each of the impulse responses recorded in the

positions used for the measurement of the mobility

was post processed to determine the decay in each

octave band of interest. Then it was possible to

compute the losses through the formula:

2.2





(13)

where f

is the central frequency of the octave band of

interest in hertz, and T

is the measured structural

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

280

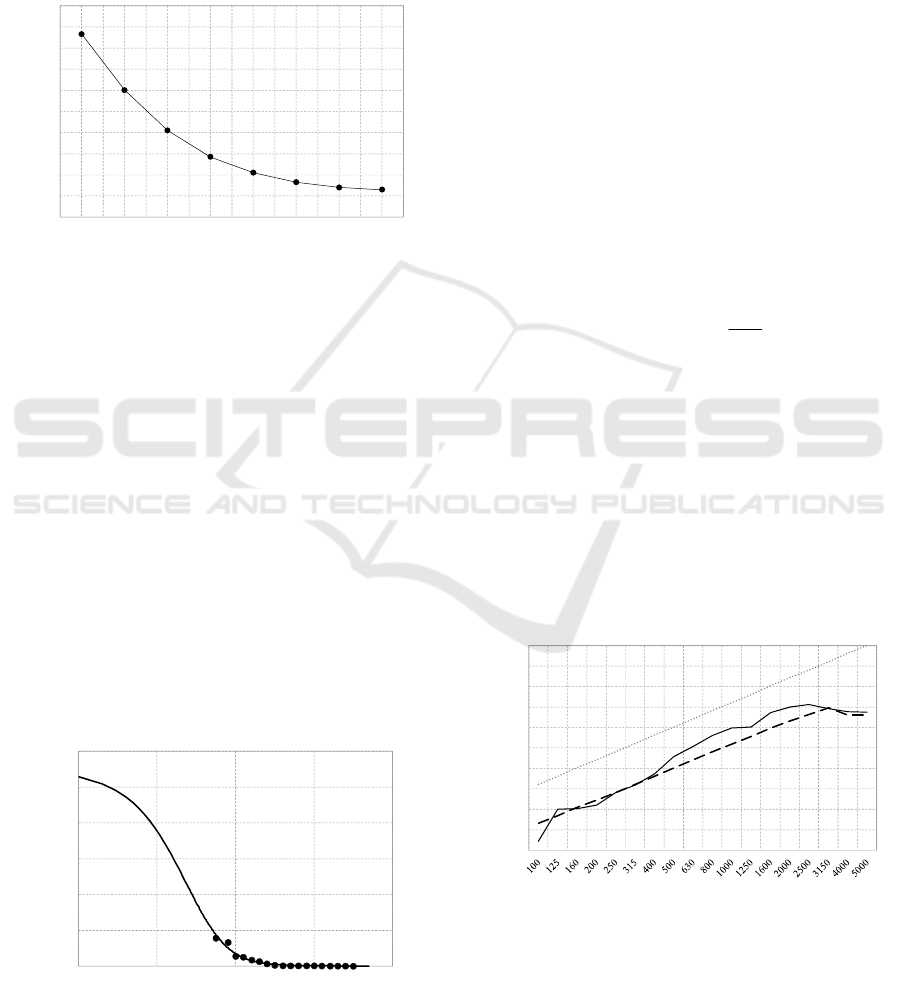
reverberation time in seconds for each frequency

band. The decay for the different frequency bands

was obtained by post processing the impulse response

signals using Adobe Audition and the Aurora plugin.

The resulting decays, computed for the frequency

bands of interest, were further post processed in order

to obtain the losses as a function of frequency (Figure

5).

Figure 5: Measured losses of the joisted floor.

4.2 Sound Reduction Index from

Mobility Measurements

Once the losses have been determined and the

apparent bending stiffness has been derived from the

mobility measurements, it is possible to compute the

sound reduction index of the panel. The computation

is carried out according to the theory described in the

previous sections, and in particular by using equation

Starting from the dimensions of the panel, its mass

for unit area and the mobility measurements, the

bending stiffness is computed in the frequency range

1 Hz – 6400 Hz. Figure 6 shows the bending stiffness

points, derived from the point mobility

measurements, and the apparent bending stiffness

function, obtained by fitting equation 11 to the

experimental data.

Figure 6: Measured bending stiffness (points) and apparent

bending stiffness (solid line).

Once the bending stiffness is computed, the

critical frequency f

can be easily determined and the

sound reduction index can be computed.

4.3 Measurement of the Sound

Reduction Index to ISO 10140-2

After performing the mobility measurements, the

joisted floor was tested according to the procedure

described in ISO 10140-2 standard in order to

determine its sound reduction index of the structure.

Two source positions were used so to have a good

average of the sound field and ten sound pressure

level measurements were performed for both the

source and the receiving rooms. The difference

between the average sound pressure level of the

source room (L

) and the average sound pressure

level of the receiving room (L

) was weighted for the

size of the partition S and the sound absorption area

of the receiving room A

to compute the sound

reduction index according to the following formula:

RRSR

LLR log10

(15)

Figure 7 shows the comparison between the sound

reduction index measured using the procedure given

by the standard and the reduction index resulting from

the mobility measurements, which displays a fairly

good agreement. The dotted line represents the sound

reduction index computed according to the mass law

for a floor having the same mass per unit area of the

one used for the experimental tests. It can be noted

that the mass law brings to a sound reduction index

which is at least 10 dB higher than the real one for

each frequency band of interest.

Figure 7: Measured (solid) vs predicted (dashed) sound

reduction index.

63 125 250 500 1000 2000 4000 6000

Losses [%]

Frequency [Hz]

50000

100000

150000

200000

250000

300000

1 10 100 1000 10000

Bending stiffness [N m]

Frequency [Hz]

Sound Reduction Index [dB]

Frequency [Hz]

Dynamic and Acoustic Properties of a Joisted Floor

281

5 CONCLUSIONS

A simple technique for the prediction of the sound

reduction index of lightweight joisted floors has been

proposed and tested. The technique has already been

adopted for predicting the dynamic and acoustic

properties of sandwich and honeycomb panels, but

seldom on lightweight, strongly orthotropic

structures. The method is based on in-situ point

mobility measurements performed on a sufficiently

high number of experimental points randomly

distributed over the specimen surface, which, once

space- and frequency-averaged, allow to compute the

apparent frequency-dependent bending stiffness of

the structure. This technique is easier to implement if

compared to other methods found in the literature,

and it allows to better take into account the

anisotropic behaviour of the specimens. The

predicted sound reduction index has been compared

to measurements performed according to the relevant

international standard, showing encouraging results.

Further experimental tests will allow to validate the

applicability of the method to other types of

structures, such as double-wall panels.

REFERENCES

Backström, D. & Nilsson, A.C., 2007. Modelling the

vibration of sandwich beams using frequency-

dependent parameters. Journal of Sound and Vibration,

300(3-5), pp.589-611.

Cremer, L., 1942. Theorie der Schalldämmung dünner

Wände bei schrägem Einfall. Akustische Zeitschrift,

7(3), pp.81-104.

Fahy, F. & Mohammed, A., 1992. A study of uncertainty in

applications of sea to coupled beam and plate systems

– Part I: Computational experiments. Journal of Sound

and Vibration, 158(1), pp.45-67.

Nightingale, T.R.T., Halliwell, R.E. & Pernica, G., 2004.

Estimating in-situ material properties of a wood joist

floor: Part 1 - Measurements of the real part of bending

wavenumber. Building Acoustics, 11(3), pp.175-96.

Nilsson, A. & Liu, B., 2016. Vibro-Acoustics, Vol. 1 and 2.

Second edition ed. Berlin Heidelberg: Springer-Verlag.

Nilsson, E. & Nilsson, A.C., 2002. Prediction and

measurement of some dynamic properties of sandwich

structures with honeycomb and foam cores. Journal of

Sound and Vibration, 251(3), pp.409-30.

Piana, E.A., 2016. A method for determining the sound

reduction index of precast panels based on point

mobility measurements. Applied Acoustics, 110, pp.72-

80.

Roelens, I., Nuytten, F., Bosmans, I. & Vermeir, G., 1997.

In situ measurement of the stiffness properties of

building components. Applied Acoustics, 52(3-4),

pp.289-309.

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

282