Recognition of Affective State for Austist from Stereotyped Gestures

Marcos Yuzuru O. Camada

, Diego St´efano

, J´es J. F. Cerqueira

, Antonio Marcus N. Lima

Andr´e Gustavo S. Conceic¸˜ao

and Augusto C. P. L. da Costa

IFbaiano, Rua Baro de Camac¸ari, 118, Centro, 48110-000, Catu, Bahia, Brazil

Electrical Engineering Department, Federal University of Bahia, Rua Arstides Novis, 02, Federac¸ ˜ao,

40210-630, Salvador, Bahia, Brazil

Electrical Engineering Department, Federal University of Campina Grande, Aprigio Veloso, 882, Bodocongo,

58109-100, Campina Grande, Para´ıba, Brazil

Keywords:

HRI, HMM, Fuzzy Inference System, Autism, Stereotyped Gesture, Assistive Robotic.

Abstract:

Autists may exhibit difﬁculty in interaction (social and communication) with others and also stereotyped

gestures. Thus, autists have difﬁculty to recognize and to express emotions. Human-Robot Interaction (HRI)

researches have contributed with robotic devices able to be mediator among autist, therapists and parents. The

stereotyped behaviors of these individuals are due to their defense mechanism from of their hypersensitivity.

The affective state of a person can be quantify from poses and gestures. This paper proposes a system is able

to infer the defense level of autists from their stereotyped gestures. This system is part of the socially assistive

robot project called HiBot. The proposed system consist of two cognitive subsystems: Hidden Markov Models

(HMM), in order to determine the stereotyped gesture, and Fuzzy Inference System (FIS), to infer activation

level of these gestures. The results of these simulations show this approach is able to infer the defense level

for an task or the presence of the robot.

1 INTRODUCTION

Autism Spectrum Disorder (ASD) belongs to the

group of pervasive developmental disorders which is

characterized by deﬁcits in social interaction, com-

munication, and stereotyped (or unusual) behaviors

(Levy et al., 2009). The autist has difﬁculty to express

and to recognize social cues, as emotion through fa-

cial and body expression and gaze eyes. The major

treatments for ASD rely on psychiatric medications,

therapies and behavioral analysis (or both).

Both software (Parsons et al., 2004) and robotic

devices (Goodrich et al., 2012) have been developed

to aid the treatment of autism. The design of such

robotic devices is naturally demand for multidisci-

plinary teams, because they may involve different

ﬁelds of health, engineering and computing.

The use of robots as social partners for autis-

tic children has already been proposed (Dautenhahn,

2003; Goodrich et al., 2012) within the ﬁeld of Hu-

man Robot Interface (HRI). Theses devices can be-

have as mediators among autists, therapist, parents.

The affective state recognition of a person is essential

for a social partner robot.

A human can express himself through verbal and

non-verbal, such as face, body and voice (Zeng et al.,

2009). Researches have focused on face expression,

but studies have also shown body cues are as powerful

as facial cues in conveying and recognizing of emo-

tions. The quantiﬁcation of the human affective state

from the poses and gestures (Camurri et al., 2003) has

been proposed as a way to recognize emotions. In ad-

dition, (Kuhn, 1999) assumes stereotyped gestures

are defense mechanisms of autists due to their hyper-

sensitivity.

For these reasons, we propose a system to affec-

tive state recognition from the stereotyped gestures

of autists in this paper. The gestures are recognized

using Hidden Markov Models (HMM). A Fuzzy In-

ference System (FIS) is used to infer the affective

state (defense level) of the autist from the gesture rec-

ognized and kinetic of joint groups.

This paper is organized as follows. In Section 2,

we deﬁne affective state, body expression, and the re-

lationship between autism. Classiﬁcation and infer-

ence tools are described in Section 3. Details of the

proposed system architecture is presented in the Sec-

tion 4. Experiments of proposed model and their re-

sults are discussed in Section 5. Finally, a general

discussions about the contributions of this paper and

Camada, M., Stéfano, D., Cerqueira, J., Lima, A., Conceição, A. and Costa, A.

Recognition of Affective State for Austist from Stereotyped Gestures.

DOI: 10.5220/0005983201970204

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 197-204

ISBN: 978-989-758-198-4

197

future works are present in Section 6.

2 BACKGROUND

2.1 Affective State

Although the human emotional state is present only

in mind, and some unconscious signals from body al-

low us to infer the mood. Particular models are es-

sential to deﬁne the human affective state. There are

two major approaches (Russell, 2003): (i) the dis-

crete approach considers the human experiences can

be expressed by a small set of emotions (e.g. hap-

piness, sadness, fear, anger, surprise and tenderness)

and these emotions are basic and experimented inde-

pendently from each other; and (ii) affective dimen-

sions approach, also called Core Affective by (Rus-

sell, 2003), assumes that emotions are appropriately

represented in an emotional plan of Valence/Arousal.

2.2 Body Expressions

Studies on body language have advanced, though they

are still few if compared with researches on facial ex-

pressions or voice. Two properties about emotional

quality from body expression are considered (Wall-

bott, 1998): (i) static conﬁguration (posture), and (ii)

dynamic or movement conﬁguration (gesture). How-

ever, most of body cues may indicate only activation

level of the person. Thus, these cues just work to

differentiate emotions. The energy (power) of move-

ments is of these cues. The highest values related to

hot anger, elated joy and terror emotions, the lowest

values corresponded to sadness and boredom.

A way to get relevant emotional features from the

full-body movements is through the Quantity of Mo-

tion (QoM) (Camurri et al., 2003). QoM can revel ac-

tivation level, for example, during dance performance

showed that movements of the limbs associated with

anger and joy are signiﬁcantly high values of QoM.

Now, let v

(f) denote the module of velocity of

each limb l at time frame f as

( f) =

˙x

( f) + ˙y

( f) + ˙z

( f), (1)

where ˙x

( f), ˙y

( f) and ˙z

( f) are cartesian velocities.

The body kinematic energy, E

tot

( f), can be an ap-

proximated by sum of the kinematic energy of each

limb as

tot

( f) =

∑

l=1

( f)

, (2)

where m

is the approximated of the limb mass based

on biometrics anthropometric tables (Dempster and

Gaughran, 1967).

2.3 Autism Spectrum Disorders

Autism Spectrum Disorder (ASD) is a neuropsychi-

atric disorder characterized by severe damage in the

socialization and communication processes. Gener-

ally, autist may also have a unusual pattern or stereo-

typed behaviors (Levy et al., 2009). Novel researches

have been indicated that several factors are associated

with the autism. Some of these known factors are ge-

netic, neurological anomalies and psychosocial risks

(Levy et al., 2009).

(Kuhn, 1999) assumes that the stereotypic behav-

iors in autists are defense mechanism due to their hy-

persensitivity. Some stereotyped gestures that can

be noted are: (i) Body Rocking (repetitive move-

ment to forward and backward of the upper torso); (ii)

Top Spinning (walk in a circle); (iii) Hand Flapping

(swing motion of the hands up and down); (iv) Head

Banging (hitting head on the ﬂoor or wall). The Head

Banging was not considered in this papers specially

because the trajectory of their movement is similar to

Body Rocking.

3 CLASSIFICATION AND

INFERENCE TOOLS

In this paper, we propose the use of two cognitive

tools for recognizing the stereotyped gesture and in-

ference of autist defense level: HMM (Subsection

3.1) and FIS (Subsection 3.2), respectively. Figure

1 (B) shows this proposed model.

3.1 Hidden Markov Models

Hidden Markov Models (HMM) are doubly stochas-

tic models, because they have an underlying Markov

chain and to transit their stochastic states symbols

need to be emitted. This emitting process is itself

a stochastic process, once it has a probability dis-

tribution over the states and to following the timing

of the transitions. Since the symbol output probabil-

ity distribution of a continuous HMM is given by a

mixture of Gaussians, a HMM can be expressed as

λ = (A, c, µ, U), where: A is the matrix of transition

probabilities; c is a set of coefﬁcients (weights for

each Gaussian in the mixture of Gaussians); µ rep-

resents the averages of each Gaussian in the mixture

and U also represents the covariance matrices of the

Gaussians.

The HMM can be applied for supervised learn-

ing pattern recognition tasks. The training process of

the HMM consists of the presentation of sequences of

outputs (training sequences) from a particular system.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

198

A training algorithm adjusts the HMM’s parameters

in such a way that when a new observation sequence

from the system being modelled is given as input to

the HMM, the probability that the model was gener-

ated will be presented in output. This discussion leads

to the three basic problems of the HMM (Rabiner,

1989; Fink, 2008):

Problem 1 - To ﬁnd the probability that the HMM λ

generated a given sequence of observation sym-

bols O = O

, O

, ..., O

, where T is the length of

the sequence (P(O|λ));

Problem 2 - To ﬁnd the underlying optimal state se-

quence Q = q

, q

, ..., q

of λ that was needed to

generate O

, O

, ..., O

(P(Q|O, λ));

Problem 3 - To adapt the model parameters in order

to maximize P(O|λ).

3.2 Fuzzy Inference System

Fuzzy Inference Systems (FIS) are widely used for

problems what the variables of the real worlds are

complex or unclear. These systems are knowledge-

based (or rule-based) and such knowledge can be ob-

tained from human experts. It can be deﬁned by fuzzy

rules of IF − THEN type. Each IF− THEN rule is

a statement in which some words are represented by

continuous membership functions (Wang, 1997). The

value of the membership function informs the degree

of membership into a fuzzy set.

(Wang, 1997) indicates three types of fuzzy sys-

tems. They differ basically about how they deal with

inputs and outputs variables of the system:

Pure Fuzzy System - It is a generic model with in-

puts and outputs based on words of natural lan-

guage;

TSK (Takagi-Sugeno-Kang) Fuzzy System - It has

input variables combine words of natural lan-

guage and Real values, but output variables are

only real values;

Mamdani - Both Fuzziﬁer and Defuzziﬁer asso-

ciates translate real input to output variables into

natural language.

Fuzzyﬁer and Defuzziﬁer are based on member-

ship functions. The membership functions translate

variable values from one universe to another. There

are different membership functions, such as Single-

ton, Gaussian, S-Shape and Z-Shape.

A Singleton membership, µ

, represents a set I

which is associated to a crisp number α

, such that,

(x) =

(

1, if x = α

0, otherwise.

(3)

A Gaussian membership, µ

, represents a set G,

where G is a gaussian curve, and it is deﬁned by aver-

age

X and standard deviation σ,

(x) = e

−

(x−

2σ

. (4)

A S-shape membership, µ

, represents a set S,

where S is a “S” curve, and it is deﬁned two parame-

ters α

and β

such that,

(x) =











0, x ≤ α



x− α

− α



, α

≤ x ≤

+ β

1− 2



x− β

− α



+ β

≤ x ≤ β

1, x ≥ β

(5)

A Z-shape membership, µ

, represents a set Z,

where Z is a “Z” curve , and it is deﬁned two param-

eters α

and β

such that,

(x) =











1, x ≤ α

1− 2



x− α

− α



, α

≤ x ≤

+ β



x− β

− α



+ β

≤ x ≤ β

0, x ≥ β

(6)

4 SYSTEM OVERVIEW

This paper is part of the robotics project called HiBot

(see Figure 1 (A)). The HiBot has been developing in

the laboratory of robotics at the Electrical Engineer-

ing Department, Federal University of Bahia. It aims

to be a platform for experiments on Human Robot In-

teraction (HRI).

The HiBot has a sets of affective actuators and

sensors. These sets are arranged by modules. The

affective actuators aim to promote interaction with

through social protocols (face and voice expressions).

That way, we deﬁne two modules: (i) Voice Synthe-

sis Module (VSM) and (ii) Facial Expression Module

(FEM). The affective sensors aim to get affective cues

conveyed by different modais, such as face, body,

voice and electroencephalography (EEG). Thus, Hi-

bot has four affective sensory modules: (i) Facial

Expression Recognition Module (FERM); (ii) Body

Expression Recognition Module (BERM); (iii) Voice

Expression Recognition Module (VERM); and (iv)

EEG Recognition Module (EEGRM). We focus on

the BERM in this paper.

The BERM gets stereotyped gestures from

autists to recognize his affective stare (defense level).

Recognition of Affective State for Austist from Stereotyped Gestures

199

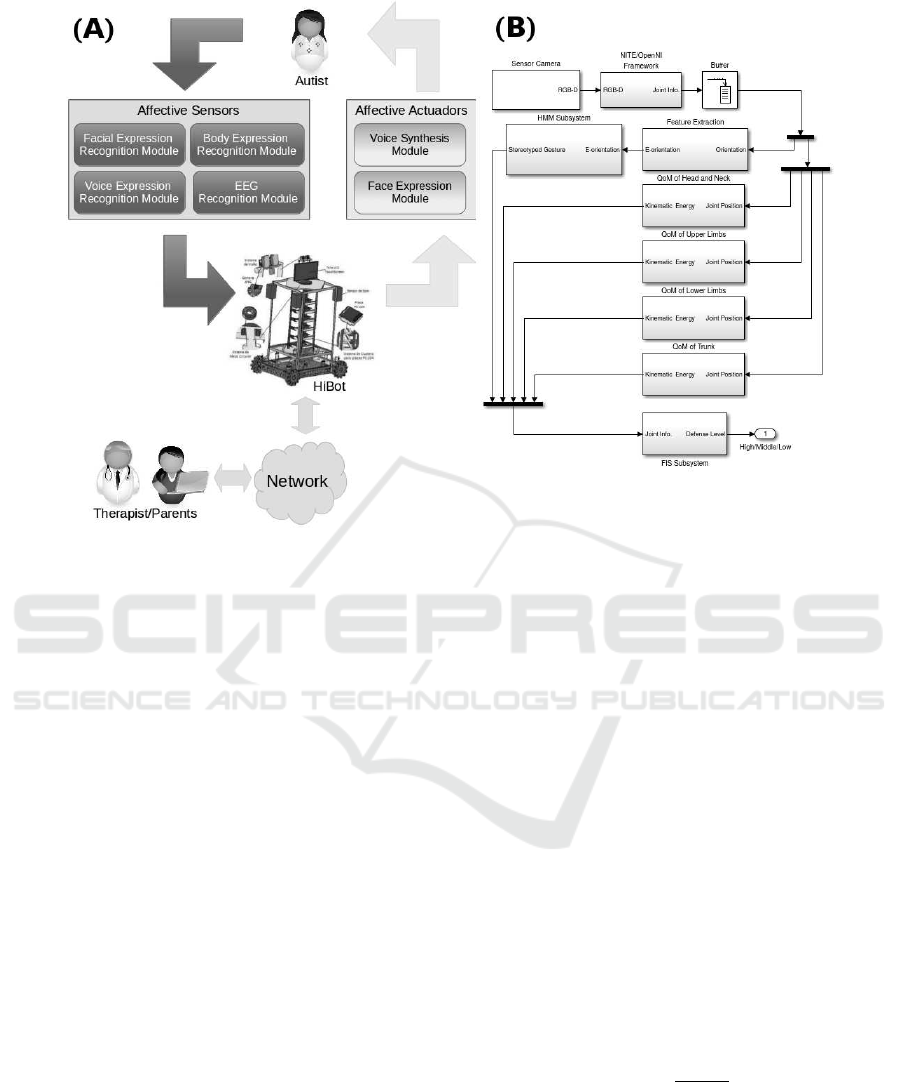
Figure 1: (A) General model of HiBot project and (B) Body Expression Recognition Module architecture.

The architecture of this module is shown in of Figure

1(B). The camera sensor is a Kinect



. This device

has a set of sensors (RGB and IR cameras, accelerom-

eter, and microphone array) and also a motorized tilt

(Microsoft, 2013). We used the RGB and IR cameras

in this paper. The IR camera provides depth infor-

mation of environment and objects. The IR Emitter

projects on the environment (and objects) several in-

frared lasers. The IR Sensor captures the IR lasers

projected. Due to this, Kinect



is able to infer the

distance (depth) between objects and IR sensor.

OpenNI/NITE frameworks are used for develop-

ment of 3D sensing middleware and applications.

Currently, they are maintained by Structure Sensor

(Structure, 2013). These software extract information

about position and orientation of the joint of an at-

tending person. The joint considered in this paper are:

head, neck, shoulders, elbows, hands (wrists), trunk,

hips, knees and foots (ankles).

The joint data (orientation and position) from 40

frames are stored in a Buffer. Joint orientation data are

processed by feature extraction algorithm (Subsection

4.1). Likewise, Quantity of Motion (Equation 2) is

applied on the joint position data.

The feature extraction algorithm results are used

by HMM Subystem (Subsection 4.2). Thus, the in-

puts of FIS Subsystem are the stereotyped gesture rec-

ognized by HMM Subsystem and the QoMs of each

joint group. FIS Subsystem must infer the defense

(stress) level of target autist.

4.1 Feature Extraction

The joint orientation data are computed by a algo-

rithm of feature extractions. This procedure was ap-

plied in order to both reduce the dimensionality (from

4 to 3) of the acquired input data and obtain a mean-

ingful representation of this data. Results from this

algorithm are the input to HMM subsystem.The fol-

lowing subsections describe the step-by-step this al-

gorithm.

4.1.1 Merging

The ﬁrst step of feature extractions algorithm consist

in merging the four quaternion streams into only one

stream. This was achieved by averaging the compo-

nents. So, let s

, for 1 ≤ i ≤ 4, denote the i-th quater-

nion stream. The resulting signal is given by

¯s =

∑

i=1

(7)

4.1.2 Frequency Spectrum

After the merging step, the frequency spectrum of the

signal ˜s, evaluated from the Fast Fourier Transform

(FFT) algorithm, is appended to it, to generate the sig-

nal s = [ ˜s FFT( ˜s)].

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

200

4.1.3 Short-Time Analysis

The Short-Time Analysis is performed with the signal

s divided in segments having M = M

+ M

samples

centered at the ˆn-th sample, given by s

ˆn

(m) = s( ˆn +

m), with −M

≤ m ≤ M

. This segment is further

multiplied (element-wise) with a Hamming window

function given by

w(n) =

(

0.54− 0.46cos(

2πn

M−1

), if 0 ≤ n ≤ M − 1

0, otherwise

(8)

being the segments obtained with an overlapping

of 30%.

The energy of each segment s

ˆn

is then calculated

ˆn

∑

j=−M

ˆn

( j), (9)

that is the ﬁrst component of the observation vectors.

Second and third componentsare respectively the ﬁrst

and second derivatives of this energy with respect to

ˆn.

4.2 HMM Subsystem Setup

In this work, the HMMs is applied to recognize ges-

tures from sequences of joint orientation acquired

with sensor camera Kinect



and stored in Buffer of

size 40. The features are extracted (see Subsection

4.1) from these sequences to generate arrays of fea-

ture vectors. These arrays, in turn, will represent the

sequence of observation symbols O. Each gesture is

associated with a HMM.

The training procedure is given by the solution

to the third problem. Let λ

= (A

, c

, µ

, U

) denote

the HMM associated to the i-th gesture, with a given

initial condition, the training procedure should adapt

these parameters using enough (typically several) ob-

servation symbols sequences O

train

from the i-th ges-

ture such that the likelihood that the resulting model

is given by

= (

, ¯c

, ¯µ

). (10)

The mechanism to evaluate the aforementioned

likelihood is given by the solution to the ﬁrst problem.

The HMM training uses 200 samples by stereotyped

gesture (100 for each activation group).

Each gesture has an HMM where Body Rocking

and Hand Flapping have 3 states, and Top Spinning

has 4 states. The number of Gaussian mixtures was

the same in all three case is 3.

4.3 FIS Subsystem Setup

FIS Subsystem infers the state of defense from the

stereotyped gesture recognized by HMM Subsys-

tem. Modelof FIS subsystem has 5 inputs: (i) Stereo-

typed Gesture, (ii) QoM Head/Neck, (iii) QoM Upper

Limbs, (iv) QoM Lower Limbs and (v) QoM Trunk.

The output of this model is Defense Level.

The ﬁrst input of the fuzziﬁes is the stereotyped

gesture recognized by HMM subsystem. Thus, this

fuzziﬁer has 3 linguistic variables: (i) Body Rocking

(BR), (ii) Hand Flapping (HF) and (iii) Top Spin-

ning (TS). These linguistic variables are deﬁned by

Singleton membership function (Equation 3). The pa-

rameters α

for these linguistic variables are respec-

tively 1, 2 and 3. Figure 2 (A) shows these linguistic

variables and its values.

The processing of QoM (see Equation (2)) is exe-

cuted in the following joint groups: Head/Neck, Up-

per Limbs,Lower Limbs and Trunk. Thus, the inputs

QoM Head/Neck, QoM Upper Limbs, QoM Lower

Limbs and QoM Trunk maps QoM of joint groups.

Figure 2(B)-(E) show 4 inputs of FIS Subsystem

with three linguistic variables: Low, Middle and High.

Linguistic variable Low is deﬁned by Z-Shape mem-

bership function (see Equation (6)). The values of pa-

rameters α

and β

are as follows,

[α

, β

] = [

Low

, Max

Low

], (11)

where

Low

, Max

Low

are average and maximum val-

ues of low subgroup related to the training samples.

Linguistic variable Middle is represented by

Gaussian membership function. The values of its pa-

rameters σ and

X are deﬁned as,

[σ,

X] = [σ

], (12)

where σ

are standard deviation and average

related to high and low subgroups of the training sam-

ples.

Finally, linguistic variable High is deﬁned by S-

Shape membership function (Equation (5)). The val-

ues of the parameters α

and β

are as follows,

[α

, β

] = [Min

High

], (13)

where Min

High

and

High

are respectively minimum

and average values of high subgroup related to the

training samples.

FIS Subsystem is based on Mamdani. That way,

we deﬁne 15 weighted rules. Table 1 shows these

rules and their respective weights.

Body Rocking and Hand Flapping are deﬁned

respectively by head/neck and upper limbs. Top

Spinning is deﬁned by lower limbs and trunk. Be-

sides that, a weight is assigned to each rule. The last

Recognition of Affective State for Austist from Stereotyped Gestures

201

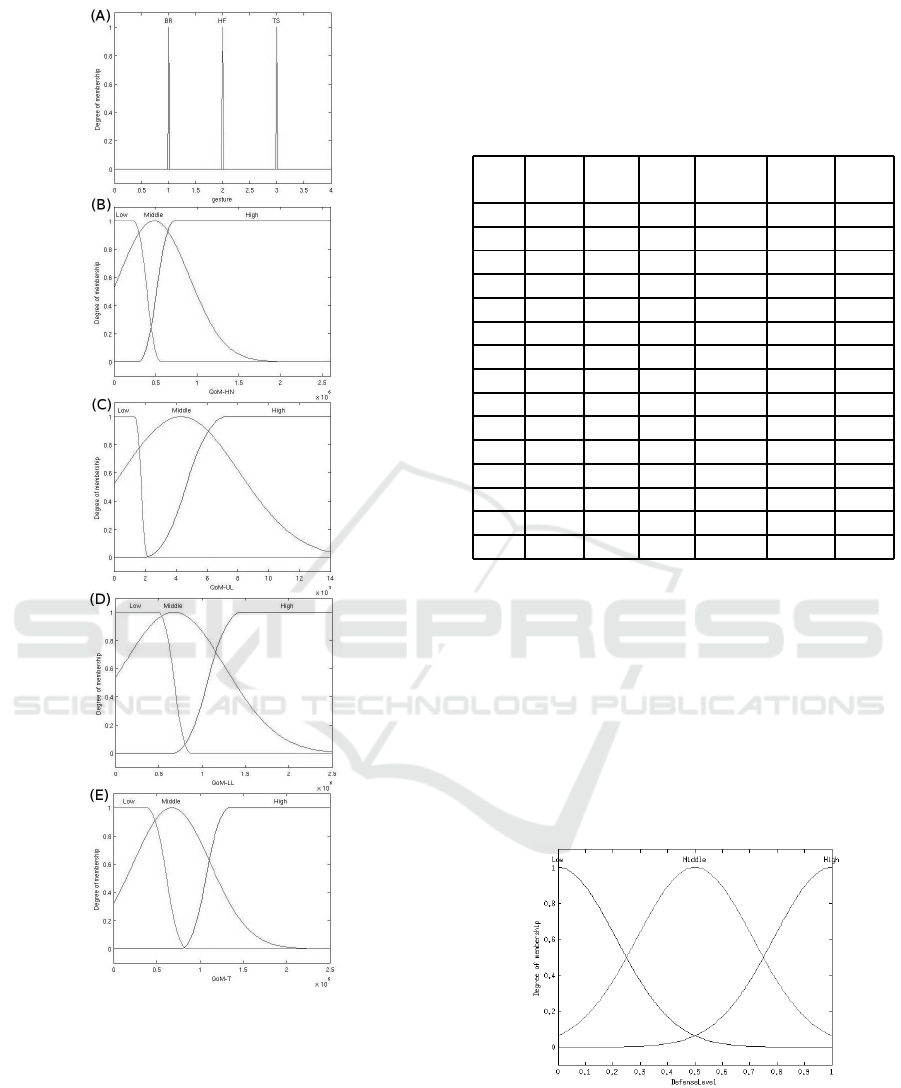
Figure 2: Input of FIS Subsystem: (A) Gesture, (B) QoM

of Head and Neck, (C) QoM of Upper Limbs, (D) QoM of

Lower Limbs, and (E) QoM of Trunk.

column (W.) in Table 1 deﬁne the values of weight of

rules. The weight is a real value that can be 0.25, 0.50

or 1.00.

The value 1.00 is assigned to the weights of the

rules related to Body Rocking and Hand Flapping

gestures. The weight values for rules of the gesture

Top Spinning depends on the difference of activation

Table 1: Deﬁning the rules and their weights (W.) with

Defense Level (D. Level) for stereotyped gestures (Ge.):

Body Rocking (BR), Hand Flapping (HF) and Top Spinning

(TS). Linguistic variables HIGH (HI.), MIDDLE (MI.) and

LOW (LO.) are deﬁned according to each QoM (Q.) of joint

groups Head/Neck (H/N), Upper Limbs (UL), Lower Limbs

(LL) and Trunk.

Ge. Q. Q. Q. Q. D. W.

H/N UL LL Trunk Level

BR HI. any any any HI. 1.00

BR MI. any any any MI. 1.00

BR LO. any any any LO. 1.00

HF any HI. any any HI. 1.00

HF any MI. any any MI. 1.00

HF any LO. any any LO. 1.00

TS any any HI. HI. HI. 1.00

TS any any HI. MI. HI. 0.50

TS any any HI. LO. MI. 0.25

TS any any MI. HI. HI. 0.50

TS any any MI. MI. MI. 1.00

TS any any MI. LO. LO. 0.50

TS any any LO. HI. MI. 0.25

TS any any LO. MI. LO. 0.50

TS any any LO. LO. LO. 0.50

level between joint groups upper limb and trunk. It

is assigned to the maximum, medium ad minimum

differentiation, 0.25, 0.50 and 1.00, respectively.

The output of the FIS Subsystem has three Gaus-

sian membership function: Low, Middle and High

(see Figure 3). The defuzziﬁer uses Centroid method,

aggregation Maximum and implication Minimum.

These membership functions are equally distributed

on the universe of values. The output of defuzziﬁer

represents the defense level of a person with autism.

Figure 3: Defuzziﬁer (defense level) with 3 Gaussian mem-

bership function: Low, Middle or High.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

202

5 EXPERIMENTS

Simulations of the BERM allow us to analyzing its

behavior and also expected results. MATLAB



and

HMM/FIS toolboxes (Murphy, 1998) were used to

simulate the BERM. MATLAB



is a high-level lan-

guage and interactive environment well known by the

community of scientists and engineers.

5.1 Methodology

For each gesture, we deﬁned two simulation scenar-

ios: high and low activation. In this way, an actor

performed repeatedly each scenarios of the stereo-

typed gestures. These gestures were recorded us-

ing Kinect



device and OpenNI/NiTE frameworks.

Thus, the RGB-D image frames were stored together

with position and orientation metadada of each joint.

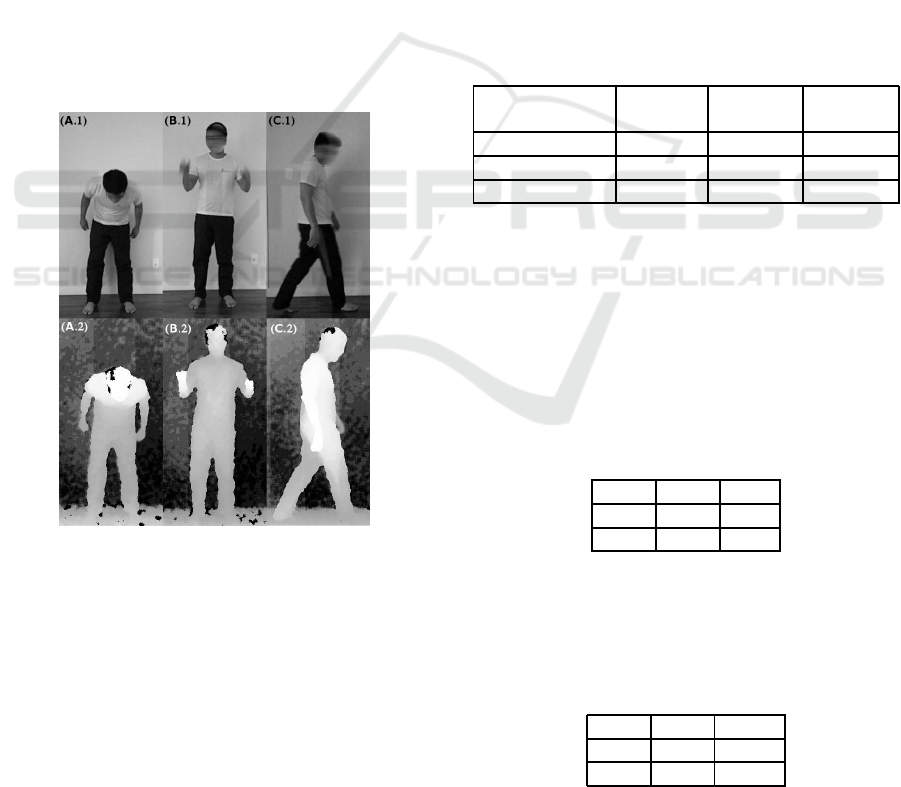
Figure 4 shows RGB-D images of stereotyped

gestures: Body Rocking (A.1 and A2), Hand Flap-

ping (B.1 and B.2) and Top Spinning (C.1 and C.2).

Figure 4: RGB-D images of stereotyped gestures performed

by an actor.

After that, the samples were manually extract.

Each sample has data about joints (position and ori-

entation) of 40 image frames. The scenarios of each

stereotyped gesture have 150 samples of which: 100

samples were used to training and other 50 were used

to simulation.

The parameter values of QoM membership func-

tion high (Equation (13)), middle (Equation (12)) and

low (Equation (11)) were deﬁned from the training

samples of HMM.

Results of these simulations present the defense

level for each gesture. In this way, we analyze

whether these results coincided with expected defense

level. These results are discussed in the followingsec-

tion.

5.2 Results and Discussion

In order to represent the statistics of the simulations

results, we use the confusion matrix. Simulation

results show the HMM Subsystem recognized all

stereotyped gestures Hand Flapping and Top Spin-

ning. Although the results for Body Rocking lower

than the other gestures, their performance was 86%

hit (see Table 2). The efﬁciency of the HMM is due

to two reasons: (i) stereotyped gestures are well-

deﬁned and distinct from themselves. (ii) the HMM

Subsystem should not differentiate among subgroups

of gestures (high or low activation).

Table 2: Confusion matrix of recognition stereotyped ges-

ture by HMM Subsystem.

Body Hand Top

Rocking Flapping Spinning

Body Rocking 86% 0% 14%

Hand Flapping 0% 100% 0%

Top Spinning 0% 0% 100%

Tables 3, 4, 5 show the performance of FIS Sub-

system for each stereotyped gesture. We consider

defense level is high for values above or equal to 0.5.

Therefore, the defense level is low for values below

0.5.

Table 3 shows the defense level for gesture Body

Rocking presents better adjustments values for high

activation (98%) than for low activation (82%).

Table 3: Confusion matrix of activation level for Body

Rocking.

High Low

High 98% 2%

Low 18% 82%

However, Table 4 shows gesture Hand Flapping

presents better adjustments values of defense level for

low activation (100%) than for high activation (96%).

Table 4: Confusion matrix of activation level for Hand Flap-

ping.

High Low

High 96% 4%

Low 0% 100%

The defense level for the gesture Top Spinning

Recognition of Affective State for Austist from Stereotyped Gestures

203

showed positive performance for the two activation

levels (see Table 5).

Table 5: Confusion matrix of activation level for Top Spin-

ning.

High Low

High 100% 0%

Low 0% 100%

The results of simulations in Tables 2, 3, 4 and 5

show relevant results for the proposed model. How-

ever, the proposed model may present lower perfor-

mance with a autist in real world than with an actor.

The idiosyncrasy of each person may inﬂuence the

gesture recognition process and inference of defense

level. In addition, the ASD (Autism Spectrum Disor-

der) presents different behavioral aspects which may

vary according to the severity. Thus, it necessary to

specify the target autistic spectrum.

Although the confusion matrix does not show the

variation in trend of defense level, this is a major re-

quirement in the process of interaction between the

robot and autistic. Thus, it is possible to analyze the

interactive process is effective or not.

6 CONCLUSION

This paper proposed a system model to infer the de-

fense level of autist from the stereotyped gestures

(body rocking, hand ﬂapping and top spinning).

These gestures were performed by an actor. The cog-

nitive model consists of HMM and FIS Subsystems.

The simulation results demonstrate this approach

is adequate and promising to recognize the defense

level from stereotyped gestures. HMM Subsystem

classiﬁes these gestures correctly. FIS Subsystem is

able to correctly infer for most simulations, showing

better results for Top Spinning.

The BERM will be used in the HiBot to recognize

the affective state of the autist, more precisely during

interaction with others sensors.

The next steps after this paper are:

1. Creating and using a database with genuine autis-

tic gestures (not actors);

2. Specifying the target autistic spectrum;

3. Integrating this module Body Expression Recog-

nition Module (BERM) with the other modules of

HiBot.

REFERENCES

Camurri, A., Lagerlof, I., and Volpe, G. (2003). Recog-

nizing emotion from dance movement: Comparison

of spectator recognition and automated techniques.

International Journal of Human Computer Studies,

59(1–2):213–225.

Dautenhahn, K. (2003). Roles and functions of robots in

human society- implications from research in autism

therapy. Robotica, 21(4):443–452.

Dempster, W. and Gaughran, G. (1967). Properties of body

segments based on size and weight. American Journal

of Anatomy, 120(7414):33–54.

Fink, G. (2008). Markov Model for Pattern Recognition:

From Theory to Applications. Berlin: Springer.

Goodrich, M., Colton, M., Brintonand, B., Fujiki, M.,

Atherton, J., and Robinson, L. (2012). Incorporating

a robot into an autism therapy team. IEEE Intelligent

Systems, 27(2):52–59.

Kuhn, J. (1999). Stereotypic behavior as a defense mecha-

nism in autism. Harvard Brain Special, 6(1):11–15.

Levy, S., Mandell, D., and Schultz, R. (2009). Autism. The

Lancet, 374(9701):1627–1638.

Microsoft (2013). Kinect for windows sensor components

and speciﬁcations. https://msdn.microsoft.com/en-

us/library/jj131033.aspx. Last accessed on Oct 21,

2013.

Murphy, K. (1998). Hidden markov model (hmm)

toolbox for matlab. http://www.cs.ubc.ca/ mur-

phyk/Software/HMM/hmm.html. Last accessed on

Jan 10, 2015.

Parsons, S., Mitchell, P., and Leonard, A. (2004). The

use and understanding of virtual environments by ado-

lescents with autistic spectrum disorders. Journal of

Autism and Developmental Disorders, 34(4):449–466.

Rabiner, L. (1989). A tutorial on hidden markov models

and selected applications in speech recognition. Pro-

ceedings of the IEEE, 77(2):257–286.

Russell, J. (2003). Core affect and the psychologi-

cal construction of emotion. Psychological Review,

110(1):145–172.

Structure (2013). Support openni.

http://structure.io/openni. Last accessed on Nov

21, 2013.

Wallbott, H. (1998). Bodily expression of emotion. Euro-

pean Journal of Social Psychology, 28(6):879–896.

Wang, L. (1997). A Course in Fuzzy Systems and Control.

PTR, Prentice Hall.

Zeng, Z., Pantic, M., Roisman, G., and Huang, T. (2009). A

survey of affect recognition methods: Audio, visual,

and spontaneous expressions. IEEE Transactions on

Pattern Analysis and Machine Intelligence, 31(1):39–

58.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

204