A Second Order Derivatives based Approach for Steganography
Jean-Franc¸ois Couchot
1
, Rapha¨el Couturier
1
, Yousra Ahmed Fadil
1,2
and Christophe Guyeux
1
1
FEMTO-ST Institute, University of Franche-Comt´e, Rue du Mar´echal Juin, Belfort, France
2
College of Engineering, University of Diyala, Baqubah, Iraq
Keywords:
Steganography, Information Hiding, Second Order Partial Derivative, Gradient, Steganalyse.
Abstract:
Steganography schemes are designed with the objective of minimizing a defined distortion function. In most
existing state of the art approaches, this distortion function is based on image feature preservation. Since
smooth regions or clean edges define image core, even a small modification in these areas largely modifies
image features and is thus easily detectable. On the contrary, textures, noisy or chaotic regions are so difficult
to model that the features having been modified inside these areas are similar to the initial ones. These regions
are characterized by disturbed level curves. This work presents a new distortion function for steganography
that is based on second order derivatives, which are mathematical tools that usually evaluate level curves. Two
methods are explained to compute these partial derivatives and have been completely implemented. The first
experiments show that these approaches are promising.
1 INTRODUCTION
The objective of any steganographic approach is to
dissimulate a message into another one in an imper-
ceptible way. In the context of this work, the host
message is an image in the spatial domain, e.g., a raw
image. A coarse steganographic technique consists
in replacing the Least Significant Bit (LSB) of each
pixel with the bits of the message to hide. On the
contrary, the goal of a steganalysis approach is to de-
cide whether a given content embeds or not a hidden
message.
Steganographic schemes are evaluated according
to their ability to face steganalyser tools. The effi-
ciency of the former increases with the number of er-
rors produced by the latter. An error is either a false
positive decision or a false negative one. In the for-
mer case, the image is abusively declared to contain a
hidden message whereas it is an original host. In the
latter case, the image is abusively declared as free of
hidden content while it embeds a message. The aver-
age error is thus the mean of these two ones. Let us se-
lect a security level expressed as a number in [0,0.5],
when developing a new steganographic scheme, the
objective is to find an approach that maximizes the
size of the message that can be embedded in any im-
age with an average error larger than this security
level.
Creating an efficient steganographic scheme aims
at designing an accurate distortion function that asso-
ciates to each pixel the ability of modifying it. This
function indeed allows the extraction the set of pix-
els that can be modified with the smallest detectabil-
ity. Highly Undetectable steGO (HUGO) (Pevn´y
et al., 2010), WOW (Holub and Fridrich, 2012), UNI-
WARD (Holub et al., 2014), STABYLO (Couchot
et al., 2015), EAI-LSBM (Luo et al., 2010), and
MVG (Fridrich and Kodovsk, 2013) are some of the
most efficient instances of such schemes. The next
step, i.e., the embedding process, is often common to
all the steganographic schemes. For instance, this fi-
nal step is the Syndrome-Trellis Code (STC) (Filler
et al., 2011) in many steganographic schemes like the
aforementioned ones.
The distortion function of HUGO evaluates for
each pixel in (x, y) the sum of the directional SPAM
features of the cover and of the image after modifying
its value P(x,y). In STABYLO and EAI-LSBM, the
distortion functions are based on edge detection. The
higher the difference between two consecutive pix-
els is, the smaller its distortion value is. WOW (and
similarly UNIWARD) distortion function is based on
wavelet-based directional filters. These filters are ap-
plied twice to evaluate the cost of ±1 modification of
the cover. In all these previously detailed schemes,
the function is designed to focus on a specific area,
namely textured or noisy regions where it is difficult
to provide an accurate model. The distortion func-
424
Couchot, J-F., Couturier, R., Fadil, Y. and Guyeux, C.
A Second Order Derivatives based Approach for Steganography.
DOI: 10.5220/0005966804240431
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 424-431
ISBN: 978-989-758-196-0
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

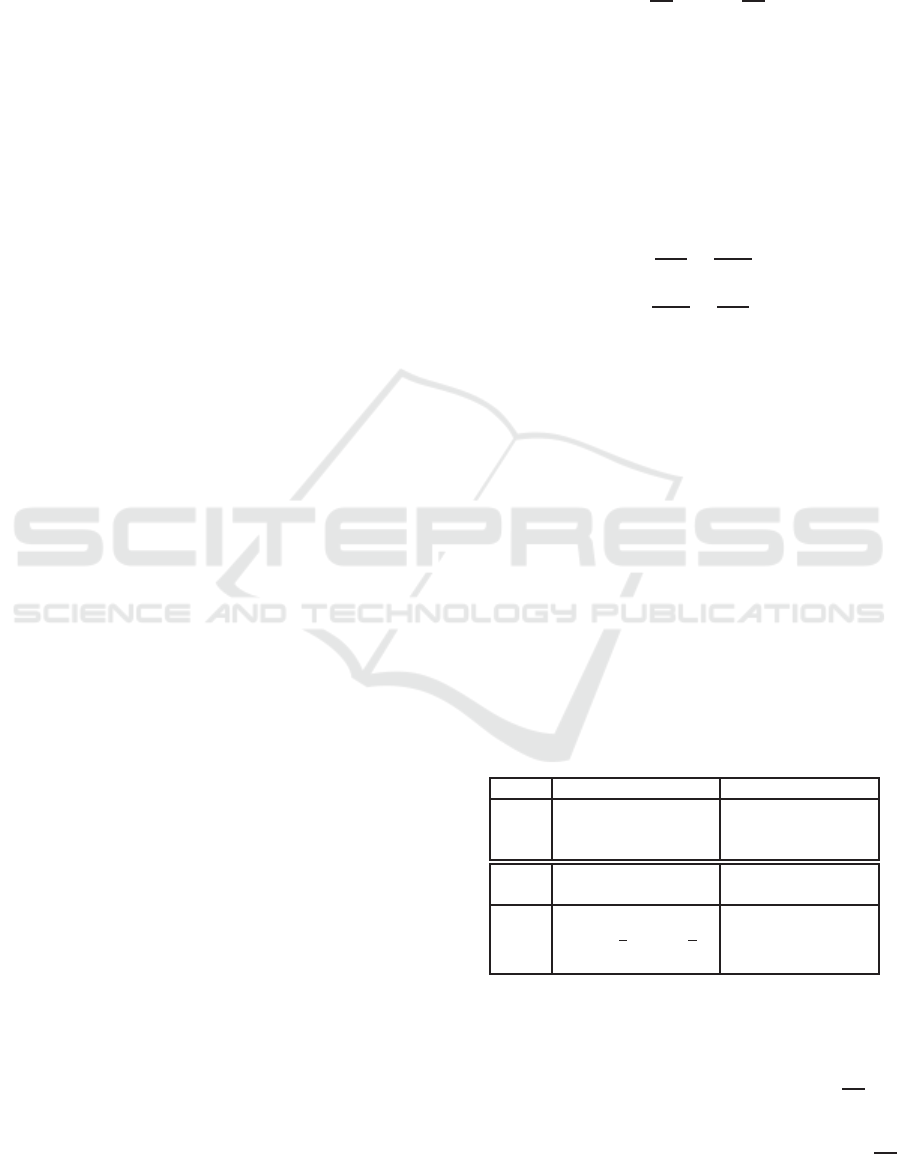
tion of MVG, for its part, is based on minimizing the
Kullback-Leibler divergence.
In all aforementioned schemes, the distortion
function returns a large value in a easy-modelable
smooth area and a small one in textured, a ”chaotic”
area, i.e., where there is no model. In other words,
these approaches assign a large value to pixels that are
in a specific level curve: modifying this pixel leads
to associating another level to this pixel. Conversely,
when a pixel is not in a well defined level curve, its
modification is hard to detect.
The mathematical tools that usually evaluate the
level curves are first and second order derivatives.
Level curves are indeed defined to be orthogonal to
vectors of first order derivatives, i.e., to gradients.
Second order derivativesallow to detect whetherthese
level curves are locally well defined or, on the con-
trary, change depending on neighborhood. Provided
we succeed in defining a function P that associates to
each pixel (x,y) its value P(x,y), pixels such that all
the second order derivatives having high values are
good candidates to embed the message bits.
However, such a function P is only known on pix-
els, i.e., on a finite set of points. Its first and second
derivatives cannot thus be mathematically computed.
At most, one can provide approximate functions on
the set of pixels. Even with such a function, ordering
pixels according to the values of the Hessian matrix
(i.e., the matrix of second order derivatives) is not a
natural task.
This work first explains how such first and second
order approximations can be computed on numerical
images (Section 2). Two proposalsto compute second
order derivatives are proposed and proven (Section 3
and Section 4). This is the main contribution of this
work. An adaptation of an existing distortion function
is studied in Section 5. A whole set of experiments
is presented in Section 6. Concluding remarks and
future work are presented in the last section.
2 DERIVATIVES IN AN IMAGE
This section first recalls links between level curves,
gradient, and Hessian matrix (Section 2.1). It next
analyses them using kernels from signal theory (Sec-
tion 2.2 and Section 2.3).
2.1 Hessian Matrix
Let us consider that an image can be seen as a numer-
ical function P that associates a value P(x,y) to each
pixel of coordinates(x,y). The variations of this func-
tion in (x
0
,y
0
) can be evaluated thanks to its gradient
∇P, which is the vector whose two components are
the partial derivatives in x and in y of P:
∇P(x
0
,y
0
) =

∂P
∂x
(x
0
,y
0
),
∂P
∂y
(x
0
,y
0
)

.
In the context of two variables, the gradient vector
points to the direction where the function has the
highest increase. Pixels with close values thus follow
level curve that is orthogonal to the one of highest in-
crease.
The variations of the gradient vector are ex-
pressed in the Hessian matrix H of second-order par-
tial derivatives of P.
H =




∂
2
P
∂x
2
∂
2
P
∂x∂y
∂
2
P
∂y∂x
∂
2
P
∂y
2




.
In one pixel (x
0
,y
0
), the larger the absolute values
of this matrix are, the more the gradient is varying
around (x
0
,y
0
). We are then left to evaluate such an
Hessian matrix.
This task is not as easy as it appears since natural
images are not defined with differentiable functions
from R
2
to R. Following subsections provide various
approaches to compute these Hessian matrices.
2.2 Classical Gradient Image
Approaches
In the context of image values, the most used ap-
proaches to evaluate gradient vectors are the well-
known “Sobel”, “Prewitt”, “Central Difference”, and
“Intermediate Difference” ones.
Table 1: Kernels of usual image gradient operators.
Name Sobel Prewitt
Kernel Ks =



−1 0 +1
−2 0 +2
−1 0 +1



Kp =



−1 0 +1
−1 0 +1
−1 0 +1



Name Central Intermediate
Difference Difference
Kernel Kc =




0 0 0
−
1
2
0 +
1
2
0 0 0




Ki =



0 0 0
0 −1 1
0 0 0



Each of these approaches applies a convolution
product∗ between a kernel K (recalled in Table 1) and
a 3× 3 window of pixel values A. The result A ∗ K is
an evaluation of the horizontal gradient, i.e.,
∂P
∂x
ex-
pressed as a matrix in R. Let K
.
be the result of a
π/2 rotation applied on K. The vertical gradient
∂P
∂y
A Second Order Derivatives based Approach for Steganography
425

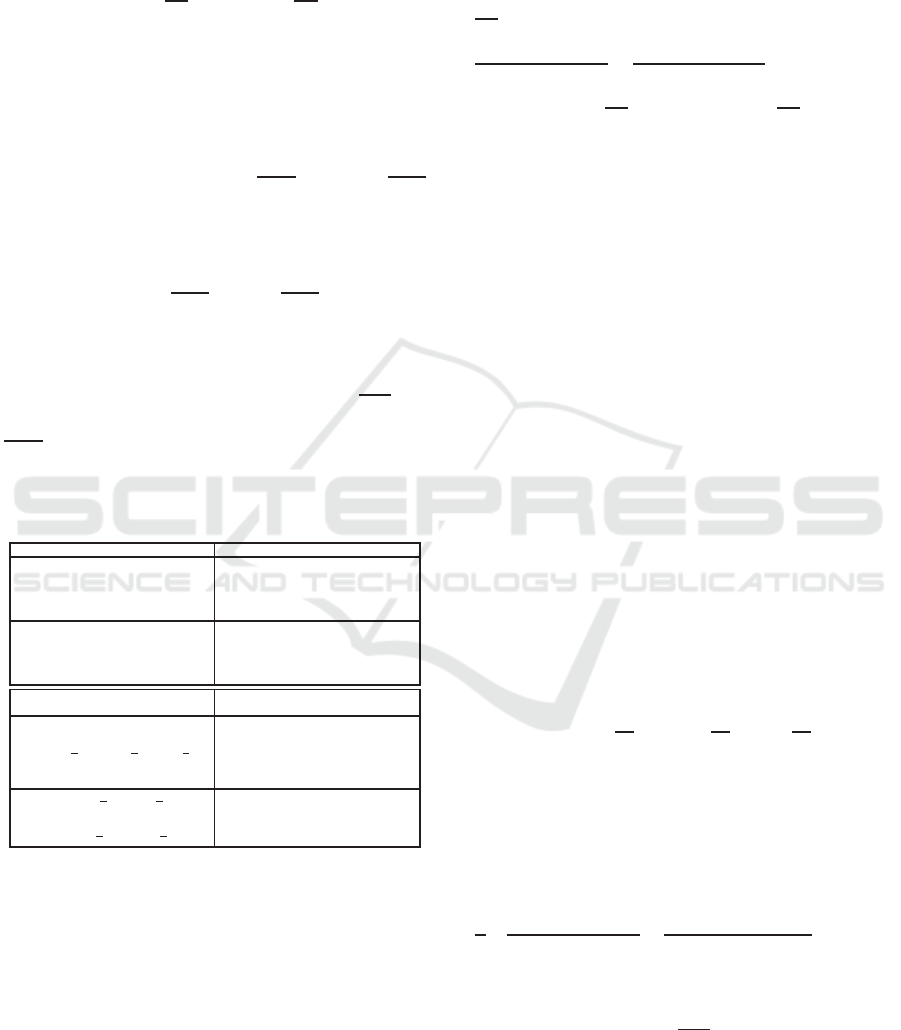
is similarly obtained by computing A ∗ K
.
, which is
again expressed as a matrix in R.
The two elements of the first line of the Hessian
matrix are the result of applying the horizontal gradi-
ent calculus first on
∂P
∂x
and next on
∂P
∂y
. Let us study
these Hessian matrices in the next section.
2.3 Hessian Matrices Induced by
Gradient Image Approaches
First of all, it is well known that
∂
2
P
∂x∂y
is equal to
∂
2
P
∂y∂x
if the approach that computes the gradient and the one
which evaluates the Hessian matrix are the same. For
instance, in the Sobel approach, it is easy to verify
that the calculus of
∂
2
P
∂x∂y
and of
∂
2
P
∂y∂x
are both the
result of a convolution product with the Kernel Ks
′′
xy
given in Table 2. This one summarizes kernels K
′′
x
2
and K
′′
xy
that allow to respectively compute
∂
2
P
∂x
2
and
∂
2
P
∂x∂y
with a convolution product for each of the usual
image gradient operator.
Table 2: Kernels of second order gradient operators.
Sobel Prewitt
Ks
′′
x
2
=





1 0 −2 0 1
4 0 −8 0 4
6 0 −12 0 6
4 0 −8 0 4
1 0 −2 0 1





Kp
′′
x
2
=





1 0 −2 0 1
2 0 −4 0 2
3 0 −6 0 3
2 0 −4 0 2
1 0 −2 0 1





Ks
′′
xy
=





−1 −2 0 2 1
−2 −4 0 4 2
0 0 0 0 0
2 4 0 −4 −2
1 2 0 −2 −1





Kp
′′
xy
=





−1 −1 0 1 1
−1 −1 0 1 1
0 0 0 0 0
1 1 0 −1 −1
1 1 0 −1 −1





Central Intermediate
Difference Difference
Kc
′′
x
2
=







0 0 0 0 0
0 0 0 0 0
1
4
0 −
1
2
0
1
4
0 0 0 0 0
0 0 0 0 0







Ki
′′
x
2
=





0 0 0 0 0
0 0 0 0 0
0 0 1 −2 1
0 0 0 0 0
0 0 0 0 0





Kc
′′
xy
=




−
1
4
0
1
4
0 0 0
1
4
0 −
1
4




Ki
′′
xy
=


0 −1 1
0 1 −1
0 0 0


The Sobel kernel Ks
′′
x
2
allows to detect whether the
central pixel belongs to a “vertical” edge, even if this
one is noisy, by considering its vertical neighbours.
The introduction of these vertical neighbours in this
kernel is meaningful in the context of finding edges,
but not very accurate when the objective is to pre-
cisely find the level curves of the image. Moreover,
all the pixels that are in the second and the fourth col-
umn in this kernel are ignored. The Prewitt Kernel
has similar drawbacks in this context.
The Central Difference kernel Kc
′′
x
2
is not influ-
enced by the vertical neighbours of the central pixel
and is thus more accurate here. However, the kernel
Kc
′′
xy
again looses the values of the pixels that are ver-
tically and diagonally aligned with the central one.
Finally, the Intermediate Difference kernel Ki
′′
x
2
shifts to the left the value of horizontal variations of
∂P
∂x
: the central pixel (0,0) exactly receives the value
P(0,2) − P(0,1)
1
−
P(0,1) − P(0,0)
1
, which is an ap-
proximation of
∂P
∂x
(0,1) and not of
∂P
∂x
(0,0). Fur-
thermorethe Intermediate Difference kernel Ki
′′
xy
only
deals with pixels in the upper right corner, loosing all
the other information.
Due to these drawbacks, we are then left to pro-
duce another approach to find the level curves with
strong accuracy.
3 SECOND ORDER KERNELS
FOR ACCURATE LEVEL
CURVES
This step aims at finding accurate level curve varia-
tions in an image. We do not restrict the kernel to
have a fixed size (e.g., 3 × 3 or 5 × 5 as in the afore-
mentioned schemes). This step is thus defined with
kernels of size (2n + 1) × (2n + 1), n ∈ {1,2,.. . ,N},
where N is a parameter of the approach.
The horizontal gradient variations are thus cap-
tured thanks to (2n+ 1) × (2n+ 1) square kernels
Ky
′′
x
2
=
















0 .. . 0
.
.
.
.
.
.
0 .. . 0
1
2n
0 .. . 0 −
2
2n
0 .. . 0
1
2n
0 .. . 0
.
.
.
.
.
.
0 .. . 0
















When the convolution product is applied on
a (2n + 1) × (2n + 1) window, the result is
1
2

P(0,n) − P(0,0)
n
−
P(0,0) − P(0,−n)
n

, which
is indeed the variation between the gradient around
the central pixel. This proves that this calculus is a
correct approximation of
∂
2
P
∂x
2
.
When n is 1, this kernelis a centered version of the
horizontal Intermediate Difference kernel Ki
′′
x
2
mod-
ulo a multiplication by 1/2. When n is 2, this kernel
is equal to Kc
′′
x
2
.
SECRYPT 2016 - International Conference on Security and Cryptography
426

The vertical gradient variations are again obtained
by applying a π/2 rotation to each horizontal kernel
Ky
′′
x
2
.
The diagonal gradient variations are obtained
thanks to the (2n + 1) × (2n + 1) square kernels Ky
′′
xy
defined by
Ky
′′
xy
=
1
4





















1
n
2
.. .
1
2n
1
n
0 −
1
n
−
1
2n
.. . −
1
n
2
.
.
. 0 .. . 0
.
.
.
1
2n
0 ... 0 −
1
2n
1
n
0 ... 0 −
1
n
0 .. . 0
−
1
n
0 ... 0
1
n
−
1
2n
0 ... 0
1
2n
.
.
. 0 .. . 0
.
.
.
−
1
n
2
.. . −
1
2n
−
1
n
0
1
n
1
2n
.. .
1
n
2





















.
When n is 1, Ky
′′
xy
is equal to the kernel Kc
′′
xy
, and
the average vertical variations of the horizontal varia-
tions are
1
4
[((P(0,1) − P(0,0)) − (P(1,1) − P(1,0)))+
((P(−1,1) − P(−1,0)) − (P(0,1) − P(0,0)))+
((P(0,0) − P(0,−1)) − (P(1,0) − P(1,−1)))+
((P(−1,0) − P(−1,−1)) − (P(0,0) − P(0,−1)))]
=
1
4
[P(1,−1) − P(1,1) − P(−1, −1)+ P(−1,1)].
which is Ky
′′
xy
.
Let us now consider any number n, 1 ≤ n ≤ N.
Let us first investigate the vertical variations related to
the horizontal vector
−−−−→
P
0,0
P
0,1
(respectively
−−−−−→
P
0,−1
P
0,0
)
of length 1 that starts from (resp. that points to)
(0,0). As with the case n = 1, there are 2 new vec-
tors of length 1, namely
−−−−→
P
n,0
P
n,1
and
−−−−−−→
P
−n,0
P
−n,1
(resp.
−−−−−→
P
n,−1
P
n,0
, and
−−−−−−−→
P
−n,−1
P
−n,0
) that are vertically aligned
with
−−−−→
P
0,0
P
0,1
(resp. with
−−−−−→
P
0,−1
P
0,0
).
The vertical variation is now equal to n. Following
the case where n is 1 to computethe average variation,
the coefficients of the first and last line around the
central vertical line are thus from left to right:
1
4n
,
−1
4n
,
−1
4n
, and
1
4n
.
Cases are similar with vectors
−−−−→
P
0,0
P
0,1
, ...
−−−−→
P
0,0
P
0,n
which respectively lead to coefficients −
1
4× 2n
, ...,
−
1
4× n.n
, and the proof is omitted. Finally, let
us consider the vector
−−−−→
P
0,0
P
0,1
and its vertical vari-
ations when δy is n − 1. As in the case where
n = 1, we thus obtain the coefficients
1
4× (n− 1)n
and −
1
4× (n− 1)n
(resp. −
1
4× (n− 1)n
and
1
4× (n− 1)n
) in the second line (resp. in the penul-
timate line) since the vector has length n and δy is
n− 1. Coefficient in the other lines are similarly ob-
tained and the proof is thus omitted.
We are then left to compute an approximation of
the partial second order derivatives
∂
2
P
∂x
2
,
∂
2
P
∂y
2
, and
∂
2
P
∂x∂y
with the kernels, Ky
′′
x
2
, Ky
′′
y
2
, and Ky
′′
xy
respec-
tively. However, the size of each of these kernels is
varying from 3 × 3 to (2N + 1) × (2N + 1). Let us
explain the approach on the former partial derivative.
The other can be immediately deduced.
Since the objectiveis to detect largevariations, the
second order derivative is approximated as the maxi-
mum of the approximations. More formally, let n, 1≤
n ≤ N, be an integer number and
∂
2
P
∂x
2
n
be the result of
applying the Kernel Ky
′′
x
2
of size (2n + 1) × (2n + 1).
The derivative
∂
2
P
∂x
2
is defined by
∂
2
P
∂x
2
= max





∂
2
P
∂x
2
1




,. . . ,




∂
2
P
∂x
2
N





. (1)
The same iterative approach is applied to compute
approximations of
∂
2
P
∂y∂x
and of
∂
2
P
∂y
2
. Next section
studies the suitability of approximating second order
derivatives when considering an image as a polyno-
mial.
4 POLYNOMIAL
INTERPOLATION OF IMAGES
FOR HESSIAN MATRIX
COMPUTATION
Let P(x,y) be the discrete value of the pixel (x,y) in
the image. Let n, 1 ≤ n ≤ N, be an integer such that
the objective is to find a polynomial interpolation on
the (2n+1)×(2n+1) window where the central pixel
has index (0, 0). There exists an unique polynomial
L : R × R → R of degree (2n+ 1) × (2n+ 1) defined
such that L(x,y) = P(x,y) for each pixel (x,y) in this
A Second Order Derivatives based Approach for Steganography
427

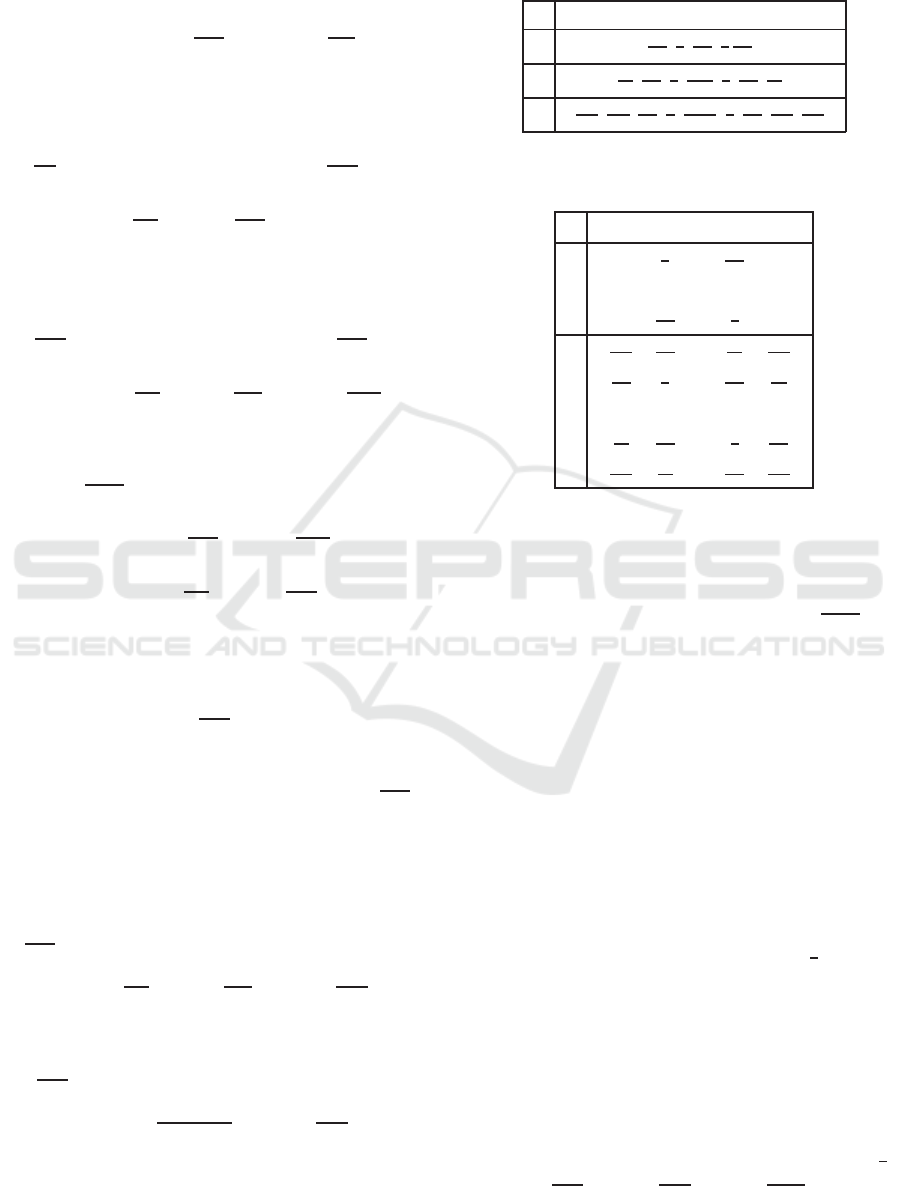
window. Such a polynomial is defined by
L(x,y) =
∑
n
i=−n
∑
n
j=−n
P(i, j)
∏
−n≤ j
′
≤n
j
′
6= j
x− j
′
i− j
′
!

∏
−n≤i
′
≤n
i
′
6=i
x−i
′
i−i
′

(2)
It is not hard to prove that the first order horizontal
derivative of the polynomial L(x,y) is
∂L
∂x
=
∑
n
i=−n
∑
n
j=−n
P(i, j)
∏
−n≤ j
′
≤n
j
′
6= j
y− j
′
j− j
′
!

∑
−n≤i
′
≤n
i
′
6=i
1
i−i
′
∏
−n≤i
′′
≤n
i
′′
6=i,i
′
x−i
′′
i−i
′′

(3)
and thus to deduce that the second order ones are
∂
2
L
∂x
2
=
∑
n
i=−n
∑
n
j=−n
P(i, j)
∏
−n≤ j
′
≤n
j
′
6= j
y− j
′
j− j
′
!

∑
−n≤i
′
≤n
i
′
6=i
1
i−i
′
∑
−n≤i
′′
≤n
i
′′
6=i,i
′
1
i−i
′′
∏
−n≤i
′′′
≤n
i
′′′
6=i,i
′
,i
′′
x−i
′′′
i−i
′′′

(4)
∂
2
L
∂y∂x
=
∑
n
i=−n
P(i, j)
∑
−n≤ j
′
≤n
j
′
6= j
1
j− j
′
∏
−n≤ j
′′
≤n
j
′′
6= j, j
′
y− j
′′
j− j
′′
!

∑
−n≤i
′
≤n
i
′
6=i
1
i−i
′
∏
−n≤i
′′
≤n
i
′′
6=i,i
′
x−i
′′
i−i
′′

(5)
These second order derivatives are computed for
each moving window and are associated to the central
pixel, i.e., to the pixel (0,0) inside this one.
Let us first simplify
∂
2
L
∂x
2
when (x,y) = (0,0) de-
fined in Equation (4). If j is not null, the index j
′
is going to be null and the product
∏
−n≤ j
′
≤n
j
′
6= j
− j
′
j− j
′
!
is null too. In this equation, we thus only consider
j = 0. It is obvious that the product indexed with j
′
is
thus equal to 1. This equation can thus be simplified
in:
∂
2
L
∂x
2
=
∑
n
i=−n
P(i,0)

∑
−n≤i
′
≤n
i
′
6=i
1
i−i
′
∑
−n≤i
′′
≤n
i
′′
6=i,i
′
1
i−i
′′
∏
−n≤i
′′′
≤n
i
′′′
6=i,i
′
,i
′′
i
′′′
i
′′′
−i

(6)
and then in:
∂
2
L
∂x
2
=
∑
n
i=−n
P(i,0)

∑
−n≤i
′
<i
′′
≤n
i
′
,i
′′
6=i
2
(i−i
′
)(i−i
′′
)
∏
−n≤i
′′′
≤n
i
′′′
6=i,i
′
,i
′′
i
′′′
i
′′′
−i

.
(7)
From this equation, the kernel allowing to evaluate
horizontal second order derivatives can be computed
Table 3: Kernels Ko
′′
x
2
for second order horizontal deriva-
tives induced by polynomial interpolation.
n Ko
′′
x
2
2

−1
12
,
4
3
,
−5
2
,
4
3
−1
12

3

1
90
,
−3
20
,
3
2
,
−49
18
,
3
2
,
−3
20
,
1
90

4

−1
560
,
8
315
,
−1
5
,
8
5
,
−205
72
,
8
5
,
−1
5
,
8
315
,
−1
560

Table 4: Kernels for second order diagonal derivatives in-
duced by polynomial interpolation.
n Ko
′′
xy
2






1
4
0
−1
4
0 0 0
−1
4
0
1
4






3














1
144
−1
18
0
1
18
−1
144
−1
18
4
9
0
−4
9
1
18
0 0 0 0 0
1
18
−4
9
0
4
9
−1
18
−1
144
1
18
0
−1
18
1
144














for any n. It is further denoted as Ko
′′
x
2
. Instances of
such matrix when n = 2, 3, and 4 are given in Table 3.
From Equation (5), kernels allowing to evalu-
ate diagonal second order derivatives (i.e.,
∂
2
L
∂y∂x
) are
computed. They are denoted as Ko
′′
xy
. Table 4 gives
two examples of them when n = 1 and n = 2. Notice
that for n = 1, the kernel Ko
′′
xy
is equal to Kc
′′
xy
.
5 DISTORTION COST
The distortion function has to associate to each pixel
(i, j) the cost ρ
ij
of its modification by ±1.
The objective is to map a small value to a pixel
when all its second order derivatives are high and a
large value otherwise. In WOW and UNIWARD the
distortion function is based on the H¨older norm with
ρ
w
ij
=




ξ
h
ij



p
+


ξ
v
ij


p
+



ξ
d
ij



p

−
1
p
where p is a negative number and ξ
h
ij
(resp. ξ
v
ij
and
ξ
d
ij
) represents the horizontal (resp. vertical and diag-
onal) suitability. A small suitability in one direction
means an inaccurate position to embed a message.
We propose here to adapt such a distortion cost as
follows:
ρ
ij
=





∂
2
P
∂x
2
(i, j)




+




∂
2
P
∂y
2
(i, j)




+




∂
2
P
∂y∂x
(i, j)





−
1
p
SECRYPT 2016 - International Conference on Security and Cryptography
428

Scheme Stego. content Changes with cover
Ky based approach
Ko based approach
Figure 1: Embedding changes instance with payload α = 0.4.
It is not hard to check that such a function has large
value when at least one of its derivatives is null. Oth-
erwise, the larger the derivatives are, the smaller the
returned value is.
6 EXPERIMENTS
First of all, the whole steganographic approach code
is available online
1
.
Figure 1 presents the results of embedding
data in a cover image from the BOSS contest
database (Pevn´y et al., 2010) with respect to the
two second order derivative schemes presented in this
work. The Ky based approach (resp. the Ko based
one) corresponds to the scheme detailed in Section 3
(resp. in Section 4). The payload α is set to 0.4 and
kernels are computed with N = 4. The central col-
umn outputs the embedding result whereas the right
one displays differences between the cover image and
the stego one. It can be observed that pixelsin smooth
area (the sky, the external access steps) and pixels in
clean edges (the columns, the step borders) are not
modified by the approach. On the contrary, an unpre-
dictable area (a monument for example) concentrates
pixel changes.
6.1 Choice of Parameters
The two methods proposed in Section 3 and in Sec-
tion 4 are based on kernels of size up to (2N + 1) ×
1
https://github.com/stego-content/SOS
(2N + 1). This section aims at finding the value of
the N parameter that maximizes the security level.
For each approach, we have built 1,000 stego images
with N = 2, 4, 6, 8, 10, 12, and 14 where the covers
belong to the BOSS contest database. This set con-
tains 10,000 grayscale 512 × 512 images in a RAW
format. The security of the approach has been eval-
uated thanks to the Ensemble Classifier (Kodovsk´y
et al., 2012) based steganalyser, which is consid-
ered as a state of the art steganalyser tool. This ste-
ganalysis process embeds the rich model (SRM) fea-
tures (Fridrich and Kodovsk´y, 2012) of size 34,671.
For a payload α, either equal to 0.1 or to 0.4, av-
erage testing errors (expressed in percentages) have
been studied and are summarized in Table 5.
Table 5: Average Testing Errors with respect to the the Ker-
nel Size.
α
N
2 4 6 8 10 12 14
Average testing 0.1 39 40.2 39.7 39.8 40.1 39.9 39.8
error for Kernel K
y
0.4 15 18.8 19.1 19.0 18.6 18.7 18.7
Average testing 0.1 35.2 36.6 36.7 36.6 37.1 37.2 37.2
error for Kernel K
o
0.4 5.2 6.8 7.5 7.9 8.1 8.2 7.6
Thanks to these experiments, we observe that the
size N = 4 (respectively N = 12) obtains sufficiently
large average testing errors for the Ky based approach
(resp. for the Ko based one). In what follows, these
values are retained for these two methods.
6.2 Security Evaluation
As in the previous section, the BOSS contest database
A Second Order Derivatives based Approach for Steganography
429

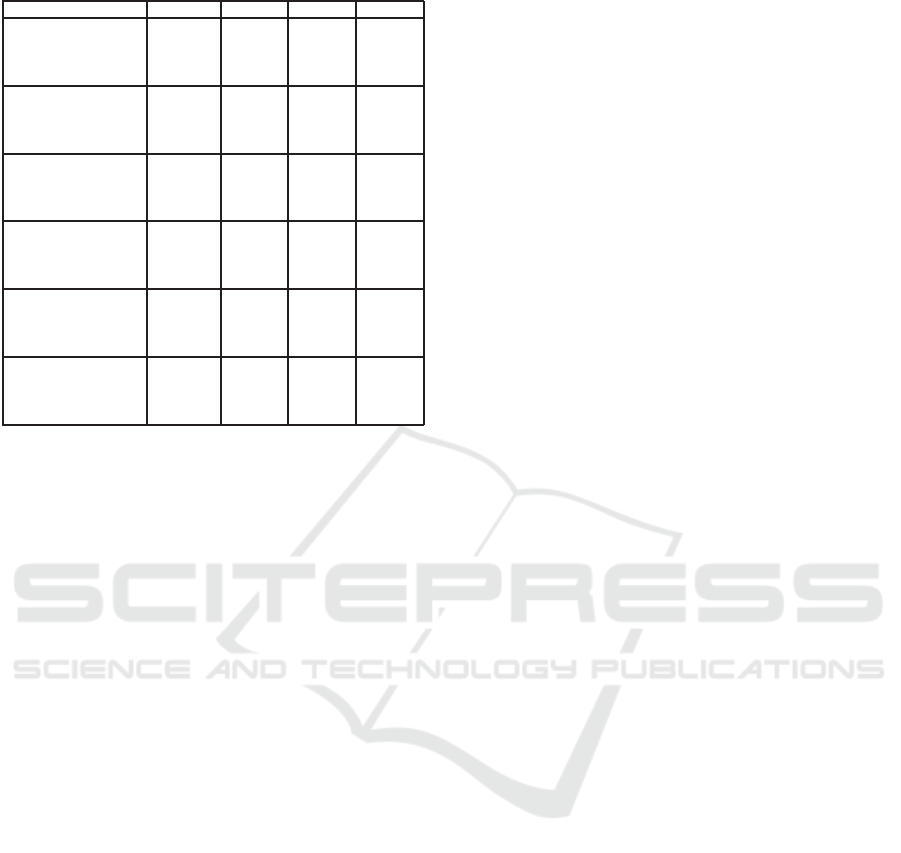
Table 6: Summary of experiments.
Payload AUC ATE OOB
WOW 0.1 0.6501 0.4304 0.3974
0.2 0.7583 0.3613 0.3169
0.3 0.8355 0.2982 0.2488
0.4 0.8876 0.2449 0.1978
SUNIWARD 0.1 0.6542 0.4212 0.3972
0.2 0.7607 0.3493 0.3170
0.3 0.8390 0.2863 0.2511
0.4 0.8916 0.2319 0.1977
MVG 0.1 0.6340 0.4310 0.4124
0.2 0.7271 0.3726 0.3399
0.3 0.7962 0.3185 0.2858
0.4 0.8486 0.2719 0.2353
HUGO 0.1 0.6967 0.3982 0.3626
0.2 0.8012 0.3197 0.2847
0.3 0.8720 0.2557 0.2212
0.4 0.9517 0.1472 0.1230
Ky based approach 0.1 0.7378 0.3768 0.3306
0.2 0.8568 0.2839 0.2408
0.3 0.9176 0.2156 0.1710
0.4 0.9473 0.1638 0.1324
Ko based approach 0.1 0.6831 0.3696 0.3450
0.2 0.8524 0.1302 0.2408
0.3 0.9132 0.1023 0.1045
0.4 0.9890 0.0880 0.0570
has been retained. To achieve a complete comparison
with other steganographic tools, the whole database
of 10,000 images has been used. Ensemble Classi-
fier with SRM features is again used to evaluate the
security of the approach.
We have chosen 4 different payloads, 0.1, 0.2, 0.3,
and 0.4, as in many steganographicevaluations. Three
values are systematically given for each experiment:
the area under the ROC curve (AUC), the averagetest-
ing error (ATE), and the OOB error (OOB).
All the results are summarized in Table 6. Let us
analyse these experimental results. The security ap-
proach is often lower than those observed with state
of the art tools: for instance with payload α = 0.1, the
most secure approach is WOW with an average test-
ing error equal to 0.43 whereas our approach reaches
0.38. However these results are promising and for two
reasons. First, our approaches give more resistance
towards Ensemble Classifier (contrary to HUGO) for
large payloads. Secondly, without any optimisation,
our approachis not so far from state of the art stegano-
graphic tools. Finally, we explain the lack of security
of the Ko based approach with large payloads as fol-
lows: second order derivatives are indeed directly ex-
tracted from polynomial interpolation. This easy con-
struction however induces large variations between
the polynomial L and the pixel function P.
7 CONCLUSION
The first contribution of this paper is to propose of
a distortion function which is based on second order
derivatives. These partial derivatives allow to accu-
rately compute the level curves and thus to look fa-
vorably on pixels without clean level curves. Two
approaches to build these derivatives have been pro-
posed. The first one is based on revisiting kernels
usually embedded in edge detection algorithms. The
second one is based on the polynomial approxima-
tion of the bitmap image. These two methods have
been completely implemented. The first experiments
have shown that the security level is slightly inferior
the one of the most stringent approaches. These first
promising results encourage us to deeply investigate
this research direction.
Future works aiming at improving the security of
this proposal are planned as follows. The authors
want first to focus on other approaches to provide
second order derivatives with larger discrimination
power. Then, the objective will be to deeply inves-
tigate whether the H¨older norm is optimal when the
objectiveis to avoid null second orderderivatives, and
to give priority to the largest second order values.
ACKNOWLEDGEMENTS
This work is partially funded by the Labex ACTION
program (contract ANR-11-LABX-01-01). Compu-
tations presented in this article were realised on the
supercomputingfacilities provided by the M´esocentre
de calcul de Franche-Comt´e.
REFERENCES
Couchot, J., Couturier, R., and Guyeux, C. (2015).
STABYLO: steganography with adaptive, bbs, and
binary embedding at low cost. Annales des
T´el´ecommunications, 70(9-10):441–449.
Filler, T., Judas, J., and Fridrich, J. J. (2011). Minimizing
additive distortion in steganography using syndrome-
trellis codes. IEEE Transactions on Information
Forensics and Security, 6(3-2):920–935.
Fridrich, J. and Kodovsk, J. (2013). Multivariate gaussian
model for designing additive distortion for steganog-
raphy. In Acoustics, Speech and Signal Processing
(ICASSP), 2013 IEEE International Conference on,
pages 2949–2953.
Fridrich, J. J. and Kodovsk´y, J. (2012). Rich models for
steganalysis of digital images. IEEE Transactions on
Information Forensics and Security, 7(3):868–882.
Holub, V., Fridrich, J., and Denemark, T. (2014). Universal
distortion function for steganography in an arbitrary
domain. EURASIP Journal on Information Security,
2014(1).
SECRYPT 2016 - International Conference on Security and Cryptography
430

Holub, V. and Fridrich, J. J. (2012). Designing stegano-
graphic distortion using directional filters. In WIFS,
pages 234–239. IEEE.
Kodovsk´y, J., Fridrich, J. J., and Holub, V. (2012). Ensem-
ble classifiers for steganalysis of digital media. IEEE
Transactions on Information Forensics and Security,
7(2):432–444.
Luo, W., Huang, F., and Huang, J. (2010). Edge adaptive
image steganography based on lsb matching revisited.
IEEE Transactions on Information Forensics and Se-
curity, 5(2):201–214.
Pevn´y, T., Filler, T., and Bas, P. (2010). Break
our steganographic system. Available at
http://www.agents.cz/boss/.
Pevn´y, T., Filler, T., and Bas, P. (2010). Using high-
dimensional image models to perform highly unde-
tectable steganography. In B¨ohme, R., Fong, P. W. L.,
and Safavi-Naini, R., editors, Information Hiding -
12th International Conference, IH 2010, Calgary, AB,
Canada, June 28-30, 2010, Revised Selected Papers,
volume 6387 of Lecture Notes in Computer Science,
pages 161–177. Springer.
A Second Order Derivatives based Approach for Steganography
431