A Dynamic Scheduling Problem in Cost Estimation
Process of EPC Projects
Nobuaki Ishii
1
, Yuichi Takano
2
and Masaaki Muraki
3
1
Faculty of Engineering, Kanagawa University, 3-27-1 Rokkakubashi, 221-8686, Kanagawa-ku, Yokoham, Japan
2
School of Network Information, Senshu University, 2-1-1, Higashimita, Tama-ku, Kawasaki, Kanagawa, Japan
3
Graduate School of Decision Science and Technology, Tokyo Institute of Technology, Tokyo, Japan
Keywords: Competitive Bidding, Discrete Event Simulation, Project Selection, Resource Allocation.
Abstract: The cost estimation process, carried out by the contractor before the start of a project, is a critical activity for
the contractor in accepting profitable EPC projects in competitive bidding situations. Thus, the contractor
should devote significant time and resources to the accurate cost estimation of project orders from clients.
However, it is impossible for any contractor to devote enough time and resources to all the orders because
such resources are usually limited. For this reason, the contractor must dynamically decide bid or no-bid on
the orders at each order arrival, and allocate the limited resources to the chosen orders. To maximize the
contractor’s profits, this study devises a heuristic scheduling method for dynamically selecting orders and
allocating the limited resources to them, on the basis of the resource requirement of the order, the contractor’s
resource utilization, and the expected profit from the order. The effectiveness of our method is demonstrated
through simulation experiments using a project cost estimation process model.
1 INTRODUCTION
In EPC (Engineering, Procurement, Construction)
projects (Pritchard and Scriven, 2011), the contractor
delivers unique facilities, such as process plants,
structures, information systems, and so on, based on
the client’s requirements for a limited period of time
under a lump sum turnkey basis. Since any EPC
project includes unique and non-repetitive activities,
many uncertainties exist in the project execution
process. Furthermore, since the project price is fixed
before the start of the project, the contractor often
faces eventual loss in EPC projects. Thus, it is
necessary for any contractor to precisely estimate the
project cost in order to determine the bidding price.
Namely, cost estimation in an EPC project is a critical
task for any contractor who seeks to increase profits
and reduce the possibility of realizing a loss, i.e.,
deficit risk, due to cost estimation error.
Cost estimation is also crucial for ensuring the
stable profits and the proper volume of accepted
orders. Inaccurate cost estimation could not only lead
to deficit orders but could also exhaust the
contractor’s resources, which are necessary to carry
out long-term deficit projects, as Ishii et al. (2014)
stated.
Moreover, a deficit order would have severely
harmful effects on the client’s business. For example,
it would generate an additional cost and/or delay the
project delivery date. Cost estimation, however, is a
complex task of predicting the costs and schedule of
projects based on the analysis of the client’s
requirements with limited data and time.
Since the quality and quantity of the data available
for cost estimation determine the accuracy of
estimated cost, a lot of high-quality data is required to
improve accuracy. In the process plant engineering,
for example,
the data and methods that are required to
attain the target accuracy of project cost estimation
have been studied
(AACE International, 2011). In any
cost estimation method, such as parametric, analogy,
and engineering (Kerzner, 2013), higher accuracy
needs more data and, accordingly, requires more
engineering Man-Hours (hereafter referred to as MH)
to acquire and analyse the data for cost estimation.
Thus, experienced and skilled human resources
who can acquire data for cost estimation and create
project plans, including uncertainties during the
project execution, are required for accurate cost
estimation.
Those resources are limited for any
contractor; furthermore, once the orders are
successfully accepted, the corresponding project
execution will also need considerable human
Ishii, N., Takano, Y. and Muraki, M.
A Dynamic Scheduling Problem in Cost Estimation Process of EPC Projects.
DOI: 10.5220/0005961101870194
In Proceedings of the 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2016), pages 187-194
ISBN: 978-989-758-199-1
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
187

resources. For these reasons, the contractor should
realize appropriate allocation of MH for cost
estimation to each order to maximize the total
expected profit under the constraint of the total MH.
The contractor should also consider the possibility of
realizing a loss, i.e., the deficit risk, due to cost
estimation error. This is because just a few deficit
orders, which produce an eventual loss due to cost
estimation error, would result in a significant
reduction of contractor’s profits when the number of
accepted orders is small.
This paper examines the cost estimation process
of EPC projects in dynamic order arrival situations
based on the previous study by Ishii et al. (2015 (b)).
Namely, we develop a heuristic method that
dynamically selects orders and allocates MH for cost
estimation to each selected order to maximize the
expected profits. For this purpose, we begin by
building a cost estimation process model, where the
cost estimation process is divided into four phases,
i.e., order selection, Class 4 estimate, Class 3 estimate,
and Class 2 estimate, based on the AACE cost
estimate classification system (AACE, 2011) that
indicates the methods, data, and the accuracy of cost
estimation in each class. We next establish the order
selection rules for deciding bid or no-bid on arrived
orders
based on the threshold function of MH
utilization with respect to the expected profit of
orders. This threshold function is created through
simulation experiments using our cost estimation
process model. We finally analyse the effectiveness
of our simulation-based heuristic method through
numerical examples.
2 RELATED WORK
A variety of studies have been conducted on project
cost estimation from the viewpoints of cost estimation
accuracy, resource allocation, order selection, and so
on.
For example, Oberlender and Trost (2001) studied
determinants of cost estimation accuracy and
developed a system for predicting accuracy. Bertisen
and Davis (2008) analysed the costs of 63 projects
and evaluated the accuracy of estimated costs
statistically. Jørgensen et al. (2012) studied the
relationship between project size and cost estimation
accuracy. Uzzafer (2013) proposed a contingency
estimation model
in consideration of the distribution
of estimated cost and the risk of software projects to
estimate contingency resources.
In addition, AACE International (2011),
Humphreys (2004), and Towler and Sinnott (2008)
demonstrated the relationship in cost estimation
accuracy and the method and data used for cost
estimation in the field of process plant engineering
projects. Furthermore, they suggested that cost
estimation accuracy is positively correlated with the
volume of MH for cost estimation.
Regarding the volume of MH for cost estimation
and cost estimation accuracy, Ishii et al. (2015 (a))
developed an algorithm that determines the bidding
prices under the limited MH for cost estimation. Their
algorithm allocates MH so as to maximize expected
profits based on the cost estimation accuracy
determined by allocated MH. In addition, Takano et
al. (2014) developed a stochastic dynamic
programming model for establishing an optimal
sequential bidding strategy in a competitive bidding
situation. Their model determines the optimal markup
in consideration of the effect of inaccurate cost
estimates. Furthermore, Takano et al. (in press)
developed a multi-period resource allocation method
for estimating project costs in a sequential
competitive bidding situation. Their method allocates
resources for cost estimation by solving a mixed
integer programming problem that is formulated by
making a piecewise liner approximation of the
expected profit functions.
Regarding the order selection in the cost
estimation process, Shafahi and Haghani (2014)
propose an optimization model that combines project
selection decisions and markup selection decisions in
consideration of eminence and previous works as the
non-monetary evaluation criterion used by owners for
evaluating bids.
Based on the above literature review, we found
that most of the studies have paid little attention to the
project cost estimation process in practical situations.
More specifically, the contractor needs to allocate
MH for cost estimation dynamically to each arrived
orders with different attributes in practice. To the best
of our knowledge, however, none of the existing
studies have investigated the project cost estimation
process in dynamic order arrival situations. In light of
these facts, this paper develops a heuristic scheduling
method for selecting orders and determining MH
allocation dynamically in consideration of the
contractor’s available MH and the orders’
profitability.
3 A MODEL OF PROJECT COST
ESTIMATION PROCESS
The project cost estimation process can be recognized
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
188

as a series of activities that starts with the arrival of
bid invitations and closes by the date of bidding. A
variety of orders arrive, and the cost of projects is
estimated through the project cost estimation process.
We decide the accuracy of cost estimation by
allocating MH to the cost estimation activities of
newly arrived orders in consideration of the MH
availability, expected profits, competitive bidding
situations, and so on. When the available MH is not
enough to estimate cost accurately, we must allocate
less MH, thereby reducing expected profit due to
inaccurate cost estimation, or no-bid on the order.
Based on the above observations, we propose a
project cost estimation process model as shown in
Figure 1 (Ishii et al. 2015 (b)). In the model, we
assume that the cost is estimated through three
classes: Class 4, Class 3, and Class 2 estimate. Each
class needs MH and a period of time for cost
estimation, and the accuracy of estimated cost
increases through the cost estimation activities in
each estimate class. The cost estimate classification
matrix (AACE, 2011) can be used as the cost
estimation accuracy in each class.
In the model, the order selection mechanism
decides whether to bid the newly arrived order or not
from the viewpoint of the volume of orders to be
accepted, the expected profits, MH availability for
cost estimation, and so on.
The selected order is first
filed in the queue for the Class 4 estimate and waits
to be assigned the MH for cost estimation by the
mechanism of MH allocation for cost estimation. If
any MH is not assigned to the order until the bidding
date, the contractor does not bid for it due to the lack
of MH. If the MH is assigned to the order, its project
cost is estimated with the accuracy of the Class 4
estimate. This order is then filed in the queue of the
Class 3 estimate and waits for MH assignment for the
Class 3 estimate. If the MH is not further assigned to
the order until the bidding date, the contractor decides
the bidding price based on the accuracy of the Class
4 estimate. By contrast, if the MH is assigned to the
order waiting in the queue of the Class 3 estimate, its
project cost is estimated with the accuracy of the
Class 3 estimate, and filed in the queue of the Class 2
estimate. The same decision is made for the orders in
the queue of the Class 2 estimate.
The project cost estimation problem, addressed
in this paper, is a kind of dynamic scheduling problem
that determines the processes dynamically for each
order arriving at a system. In our problem, however,
the quality of the deliverables, i.e. accuracy of cost
estimation of each order, are determined dynamically
under the conditions of resource availability and due
date of the order so as to maximize the total profits.
On the contrary, in the standard scheduling problems
(Jacobs et al. 2011), the quality of the deliverables are
predetermined and orders are scheduled so as to
minimize the makespan. From this perspective, the
project cost estimation problem in this study can be
recognized as a new dynamic scheduling problem.
Figure 1: A project cost estimation process model.
4 HEURISTIC METHOD
This section shows a heuristic scheduling method
based on the project cost estimation process shown in
Figure 1. The heuristic method consists of two
mechanisms, i.e. order selection, and MH allocation
for cost estimation. The order selection mechanism
selects orders for cost estimation based on order
selection rules. The MH allocation mechanism
assigns the MH for cost estimation to each selected
order, so as to maximize the expected profits from
orders.
Our heuristic method is developed based on the
following assumptions:
Assumptions:
1) Orders for cost estimation arrive randomly;
2) Expected profit, required MH and periods for
cost estimation of each estimate class are
predetermined;
3) Probability of a successful bid of each order is
predetermined.
Since EPC contractors can collect their own data
on past projects and market situations, the
assumptions 2) and 3) are appropriate.
4.1 Order Selection Mechanism
(1) Order selection method
The order selection method is based on the financial
evaluation criteria and consists of the following two
steps:
Queue
for
Class 4
Class 4
estimate
Queue
for
Class 3
Class 3
estimate
Queue
for
Class 2
Class 2
estimate
MH allocation
for cost
estimation
Condition of MH
availability
MH for cost estimation
Bidding
price
decision
Order
selection
Decline bid
invitation
Results of cost estimation
Newｌｙ arrived
orders
Goal: The volume of orders, Expected profits
Condition of MH availability
Orders for bid
No-bid
orders due to
lack of MH
Total volume of MH
for cost estimation
No-bid orders
A Dynamic Scheduling Problem in Cost Estimation Process of EPC Projects
189

Step 1: Calculate the expected profit per MH for cost
estimation of the new arrival order i as follows:
EPPC
i
= EP
i
/ EM
i
(1)
where EPPC
i
is the expected profit per MH for
cost estimation of order i, EP
i
is the expected
profit of order i, and EM
i
is the volume of MH
required to estimate the cost of order i. In this
paper, EPPC
i
is calculated based on the Class 2
estimate in AACE cost estimate class (AACE,
2011).
Step 2: Make the bid/no-bid decision on the new
arrival order by considering EPPC
i
of the order
and the contractor’s MHU, which is the volume of
MH being utilized for cost estimation at the time
of new order arrival. For this purpose, we use a
threshold function MHU
up
(EPPC
i
), which
indicates the upper limit of MHU in selecting
order i for cost estimation, as follows:
- The contractor selects the new arrival order i for
cost estimation if MHU is
lower than
MHU
up
(EPPC
i
);
- Otherwise, the contractor decides not to bid on
the order.
The contractor can expect higher profits from the
order by estimating its project cost in a higher cost
estimate class. However, more MH is required for
estimating cost in a higher cost estimate class. In the
above steps, the new arrival orders with low expected
profits are not selected for cost estimation when large
volume of MH is being utilized for cost estimation.
This order selection method eliminates a possible
shortage of MH for cost estimation and, accordingly,
allows the contractor to focus on estimating cost of
profitable orders. In other words, our order selection
method works to maintain the balance between
order’s profitability and contractor’s MH utilization
so that the contractor’s expected profits are
maximized in dynamic order arrival situations.
(2) Determination of threshold function
In our model, orders with different attributes arrive
randomly in a project cost estimation process. Thus
the MH utilization changes dynamically and
unpredictably. Consequently, it is very difficult to
find a threshold function MHU
up
(EPPC
i
) for
maximizing contractor’s expected profits.
In view of these observations, we develop a
simulation-based heuristic method by using the
simulation model shown in Figure 1. This method
searches three threshold points, P1(E
1
, N
1
), P2(E
2
, N
2
)
and P3(E
3
, N
3
), sequentially by applying them in the
order selection mechanism. As shown in Figure 2, the
no-bid area is expressed as follows:
},|),{(
3
1 kkk
NMHUEEPPCMHUEPPCU 

(2)
The threshold function MHU
up
(EPPC
i
) marks the
boundary between the no-bid area and cost estimation
area. The procedure of the simulation based method
is described as follows:
Step 1: Set all the threshold points to (0, 0).
Step 2: Search P2(E
2
, N
2
) that maximizes the
expected profit by running a simulation under the
current conditions, i.e., order arrival interval, cost
estimation period and required MH in each class
of cost estimate, and expected profit of each order.
Step 3: Search P1(E
1
, N
1
) that maximizes the
expected profit by running a simulation, where
P2(E
2
, N
2
) is fixed to the value searched in Step 2.
Step 4: Search P3(E
3
, N
3
) that maximizes the
expected profit by running a simulation, where
P1(E
1
, N
1
) and P2(E
2
, N
2
) are fixed to the values
searched in Steps 2 and 3.
Step 5: Define MHU
up
(EPPC
i
) as the boundary
formed by P1(E
1
, N
1
), P2(E
2
, N
2
) and P3(E
3
, N
3
)
as shown in Figure 2.
Figure 2: Area of bid/no-bid decision.
4.2 Allocation of MH for Cost
Estimation
For the allocation of MH for cost estimation, we shall
use a dispatching approach, as is the case with the
dynamic scheduling problem in production systems
(Jacobs et al. 2011).
Specifically, when MH is released from cost
estimation of an order, this approach selects an order
based on the dispatching rules, which prioritize orders
in the queue of each estimate class. The selected order
is subsequently assigned the required MH for its
estimate class. If the required MH is more than the
MH available, the selected order waits in the queue
until the required MH is released.
One can use well-known dispatching rules for the
MHU [M MH]
0.0 0.5 1.0 ・・・・・・・・・・・・E
N
・
・
・
2
0
EPPC [$/MH ]
P1(E
1
, N
1
)
No-bid area
Cost estimation area
P2(E
2
, N
2
)
P3(E
3
, N
3
)
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
190

allocation of MH, such as FIFO, SPT, and EDD
(Jacobs et al. 2011). In addition, dedicated rules for a
project cost estimation process can also be designed.
5 NUMERICAL EXAMPLES
This section evaluates the effectiveness of our
simulation-based heuristic scheduling method. For
the simulation experiments, we use a general-purpose
simulation system AweSim! (Pritsker and O’Reilly,
1998).
5.1 Design of Simulation Experiments
To determine the threshold function MHU
up
(EPPC
i
),
we use the scenario selection system developed by
Nelson et al. (2001). This system statistically
compares the results of simulation and chooses
sequentially the best threshold points P2(E
2
, N
2
),
P3(E
3
, N
3
), P1(E
1
, N
1
) from candidate points given by
us. The volume of MH is set to 16,000 MH per period,
i.e., 16 [M MH], and the simulation period is set to
1200.
It is supposed that there are orders of the three
sizes, i.e., Small, Medium, Large, in our simulation
experiments. For these orders, we consider three
cases—Case 1, Case 2, and Case 3—that have
different expected profit of the Class 3 estimate, as
shown in Table 1. In addition, we consider three sub-
cases—Case A, Case B, and Case C—based on the
order arrival intervals defined by the triangular
distribution, as shown in Table 2. In what follows,
Case 1.A means that Case 1 and Case A are
considered. Table 3 shows parameters of triangular
distribution that represents the probability of order
acceptance in each order size. It follows that by
bidding for an order, the expected profit shown in
Table 1 is gained with the associated probability of
order acceptance. Table 4 shows cost estimation
conditions of each cost estimate class, i.e., total
periods available for cost estimation (due date for
bidding), required periods for cost estimation, and
required MH for cost estimation.
Our simulation experiments evaluated each case
by using the following order selection rules and
dispatching rules:
1) Order selection rule
No selection: All the arrived orders are selected for
cost estimation.
MHU basis: Orders are selected for cost estimation
by the heuristic method described in Section 4.
2) Dispatching rule for allocating MH for cost
estimation
FIFO: Orders are selected for allocating MH on a
first-in first-out basis.
HEPF: Order of the largest increment of EPPC is
selected first for allocating MH.
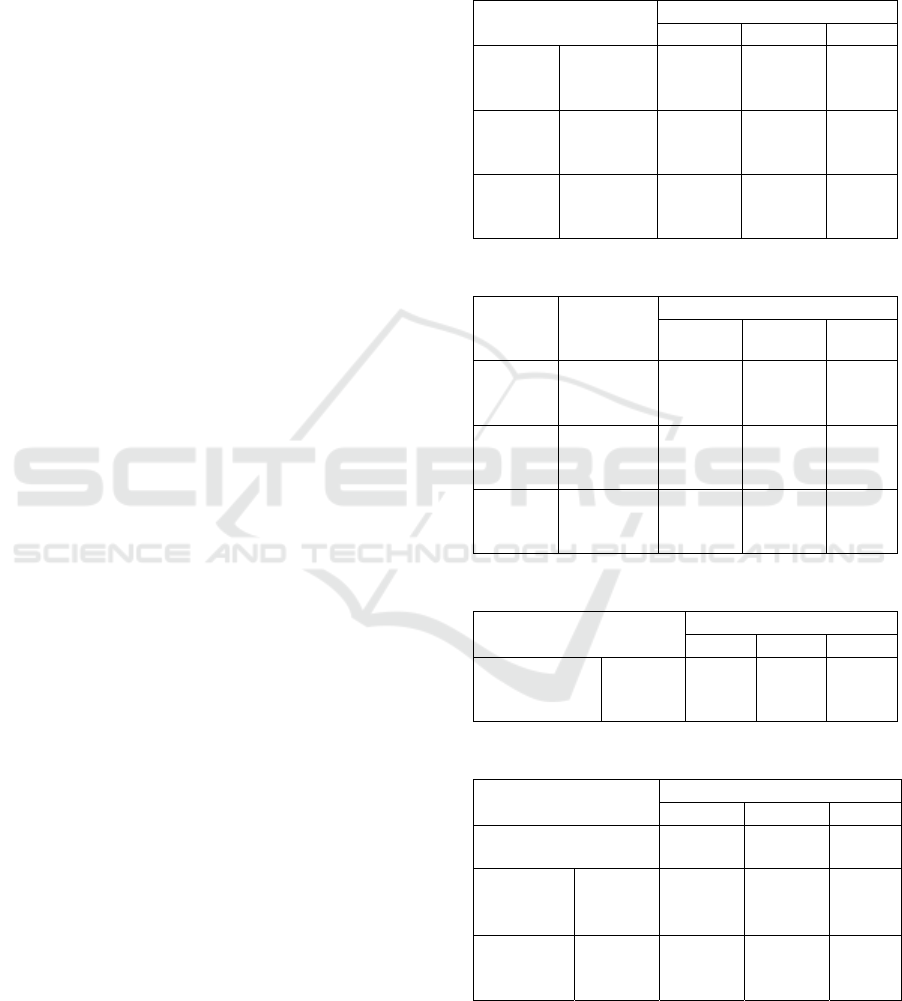
Table 1: Expected profit of orders (All cases) [MM$].
Order size
Small Medium Large
Case 1 Class 4
Class 3
Class 2
0.5
5
20
1
10
40
1.5
15
60
Case 2 Class 4
Class 3
Class 2
0.5
10
20
1
20
40
1.5
30
60
Case 3 Class 4
Class 3
Class 2
0.5
15
20
1
30
40
1.5
45
60
Table 2: Order arrival interval [Orders/Period].
Parameters
of triangular
distribution
Order size
Small Medium Large
Case A Min.
Mode
Max.
1.05
1.50
1.95
2.70
3.00
3.90
3.15
4.50
5.85
Case B Min.
Mode
Max
0.84
1.20
1.56
1.68
2.40
3.12
2.52
3.60
4.68
Case C Min.
Mode
Max
0.70
1.00
1.30
1.40
2.00
2.60
2.10
3.00
3.90
Table 3: Probability of order acceptance (All cases).
Order size
Small Medium Large
Parameters of
triangular
distribution
Min.
Mode
Max.
0.05
0.20
0.90
0.05
0.30
0.90
0.05
0.40
0.90
Table 4: Cost estimation conditions (All cases).
Order size
Small Medium Large
Total periods available
for cost estimation
8 8 8
Periods for
cost
estimation
Class 4
Class 3
Class 2
1
2
3
1
2
3
1
2
3
MH for cost
estimation
[M MH]
Class 4
Class 3
Class 2
1
2
3
2
3
4
3
4
6
5.2 Results of Simulation Experiments
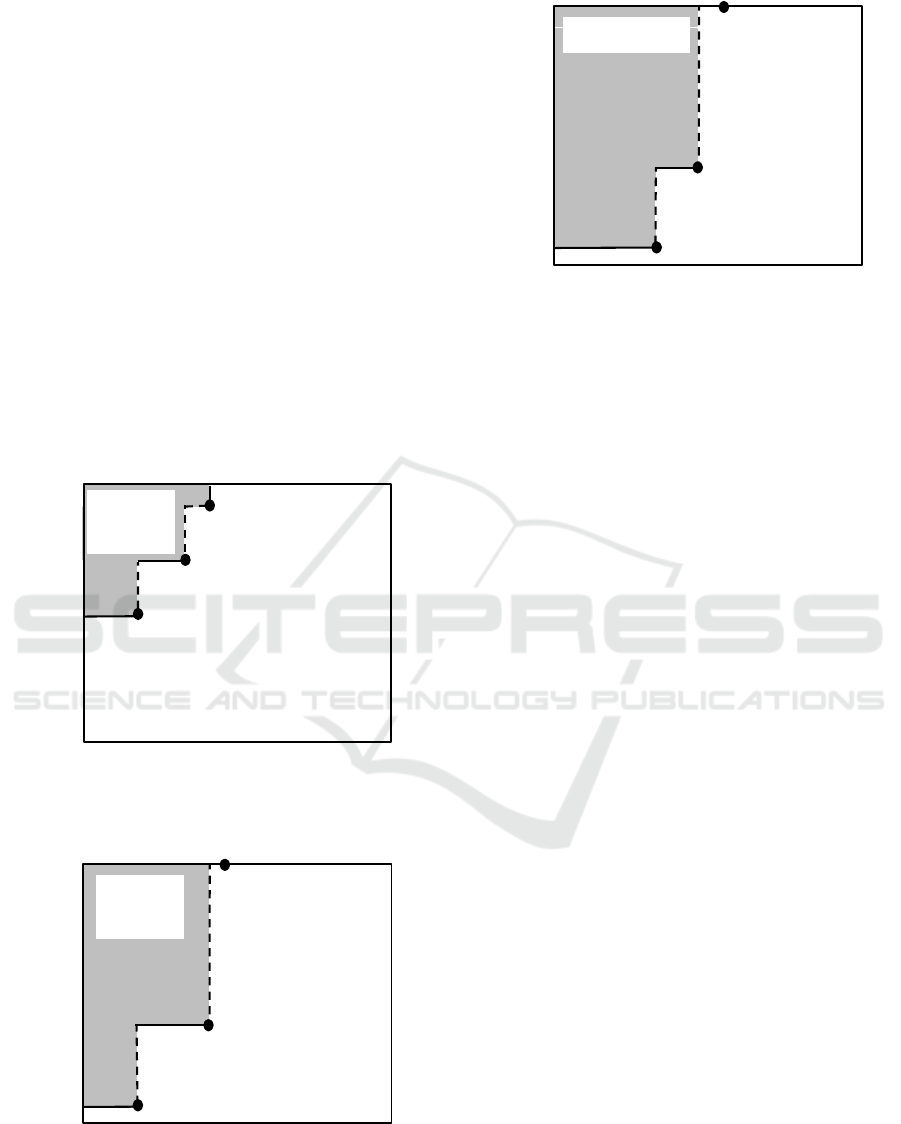
Figures 3, 4, and 5 depict the threshold function
A Dynamic Scheduling Problem in Cost Estimation Process of EPC Projects
191

MHU
up
(EPPC
i
) together with the threshold points
P1(E
1
, N
1
), P2(E
2
, N
2
) and P3(E
3
, N
3
) determined by
our simulation-based heuristic method for Cases 1.A,
1.B, and 1.C, respectively. For example, the arrived
order with 0.8 EPPC and 10 MHU is the one for the
cost estimation in Case 1.A, however, not the one for
the cost estimation in Cases 1.B and 1.C.
We can see in the figures that the no-bid area
becomes wider according to the increase of the
number of arrived orders in the cost estimation
process. Indeed, Case 1.C, where orders arrive most
frequently among all cases, has the widest no-bid area.
It is also found from the figures that in making
bid/no-bid decisions, Case 1.C puts a high priority on
the order’s expected profit, whereas Case 1.A takes
into account both the order’s expected profit and the
contractor’s MH utilization. This implies that
contractors should pay attention to its MH utilization
for cost estimation especially when the number of
arrival orders is limited.
Figure 3: Area of bid/no-bid decision in Case 1.A.
Figure 4: Area of bid/no-bid decision in Case 1.B.
Figure 5: Area of bid/no-bid decision in Case 1.C.
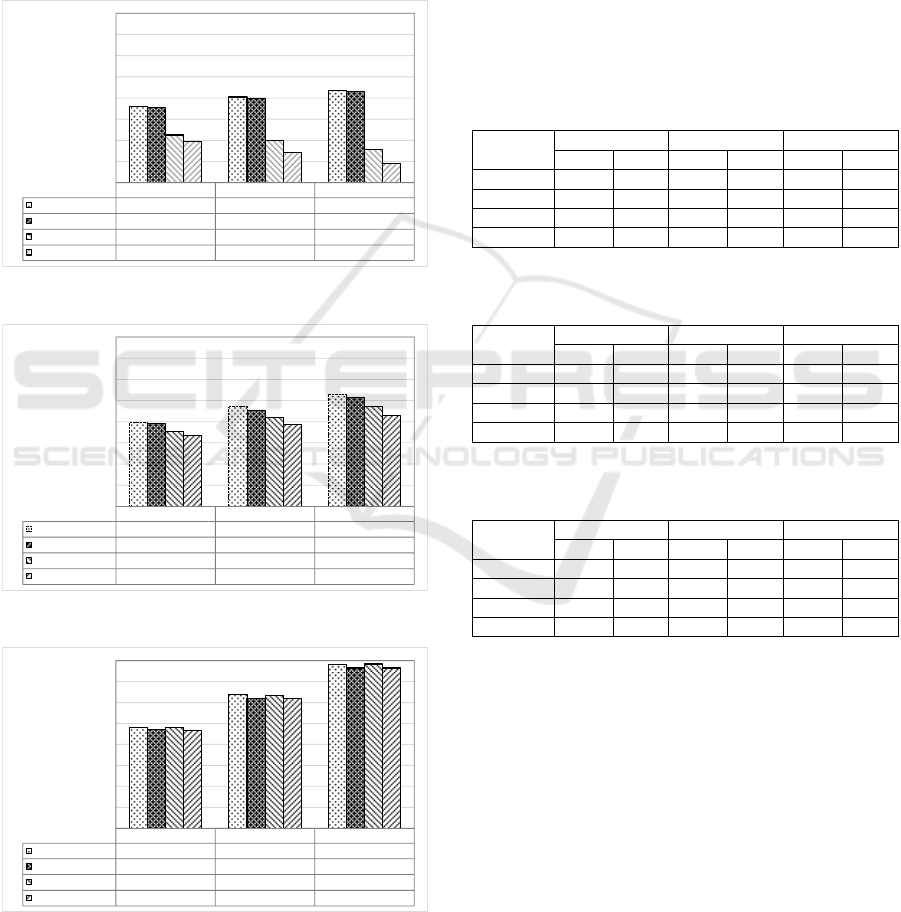
Figures 6, 7, and 8 show the expected profits of
each combination of order selectin rules and MH
allocation rules. Regarding the order selection rule,
the MHU basis rule gains larger expected profits than
the no selection rule does. For example, in Case 1.C,
the expected profit by MHU basis HEPF is 167
[MM$], and that by no selectin HEPF is 111 [MM$].
In addition, the improvement in the expected profits
by the MHU basis rule increases according to the
increase of the number of arrived orders in the project
cost estimation process. In fact, the ratio of
improvement in the expected profits by MHU basis
HEPF is about 22%, 34%, and 50% against the no
section rule, in Cases 1.A, 1.B and 1.C, respectively.
On the other hand, as shown in Figure 8, the
effects of the MHU basis rule on the expected profits
are very small in Case 3. The main reason is that in
Case 3, the expected profits of the Class 3 estimate
are close to those of the Class 2 estimate as shown in
Table 1. No selection rules allocate MH for cost
estimation evenly to all the orders and, accordingly,
increase the number of Class 3 estimates. As a result,
this rule works well only in Case 3. By contrast, the
MHU basis rules make bid/no-bid decisions based on
the threshold functions as shown in Figures 3-5, and
thus, they work effectively in all the cases.
Regarding the dispatching rules for allocating MH,
HEPF rules perform slightly better than FIFO rules.
However, they make no significant difference in the
expected profits, especially when the MHU basis rule
is used for order selection.
Tables 5, 6, and 7 show the ratio of cost estimate
class determined by the HEPF rule. The MHU basis
rule makes many Class 2 estimates compared with the
no selection rule in Cases 1 and 2. Additionally, we
observe that the number of no-bid orders is also large
in the MHU basis rule. For example, the MHU basis
rule makes no-bid decisions on 38.7% of arrived
MHU [M MH]
0.0 0.5 1.0 1.5 2.0 2.5
16
14
12
10
8
6
4
2
0
EPPC [MM$/M MH ]
(0.4, 8)
(0.8, 11)
(1.0, 15)
No-bid
area
Cost estimation area
MHU [M MH]
0.0 0.5 1.0 1.5 2.0 2.5
16
14
12
10
8
6
4
2
0
EPPC [MM$/M MH ]
(0.4, 1)
(1.0, 6)
(1.2, 16)
No-bid
area
Cost estimation area
MHU [M MH]
0.0 0.5 1.0 1.5 2.0 2.5
16
14
12
10
8
6
4
2
0
EPPC [MM$/M MH ]
(0.8, 1)
(1.2, 6)
(1.4, 16)
No-bid area
Cost estimation area
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
192

orders in Case 1.A as shown in Table 5. In the case of
the MHU basis rule, the ratio of no-bid orders
increases according to the increase of number of
arrived orders in the project cost estimation process.
Namely, the ratio of no-bid orders increases as 38.7%,
50.4%, and 62.0% according to the increase of the
number of arrived orders in Case 1.A, Case 1.B, and
Case 1.C. This maintain the number of the Class 2 and
Class 3 estimates, which bring more expected profits
than the Class 4 estimate.
Figure 6: Expected profits in Case 1.
Figure 7: Expected profits in Case 2.
Figure 8: Expected profits in Case 3.
In our simulation, the average number of arrived
orders is 1465, 1827, and 2195 in Cases A, B, and C,
respectively. In Case 3, however, the ratio of cost
estimate class provided by the MHU basis rules is
very similar to that provided by no selection rules as
shown in Table 7. Since the expected profits per MH
of the Class 3 estimate is higher than that of the Class
2 estimate in Case 3, the MHU basis rule focuses MH
for cost estimation on the Class 3 estimates.
These observations confirm that our heuristic
method for the order selection works well to allocate
MH for cost estimation appropriately so that the
expected profits from orders are maximized in the
dynamic order arrival situations.
Table 5: Ratio of cost estimate class in Case 1 HEPF rule
(MHU: MHU basis, No: No selection) [%].
Case 1.A Case 1.B Case 1.C
MHU No MHU No MHU No
No-bid 38.7 0.0 50.4 0.0 62.0 0.0
Class 4 0.0 0.0 0.0 0.1 0.0 0.6
Class 3 7.6 50.1 8.5 71.9 6.2 87.0
Class 2 53.7 49.9 41.2 28.1 31.8 12.3
Table 6: Ratio of cost estimate class in Case 2 HEPF rule
(MHU: MHU basis, No: No selection) [%].
Case 1.A Case 1.B Case 1.C
MHU No MHU No MHU No
No-bid 31.8 0.0 32.7 0.0 47.4 0.0
Class 4 0.0 0.0 0.0 0.1 0.0 0.6
Class 3 13.3 50.1 28.4 71.9 21.5 87.0
Class 2 54.9 49.9 38.9 28.1 31.1 12.3
Table 7: Ratio of cost estimate class in Case 3 HEPF rule
(MHU: MHU basis, No: No selection) [%].
Case 1.A Case 1.B Case 1.C
MHU No MHU No MHU No
No-bid 0.6 0.0 0.7 0.0 0.9 0.0
Class 4 0.0 0.0 0.1 0.1 0.6 0.6
Class 3 49.4 50.1 71.3 71.9 85.5 87.0
Class 2 50.0 49.9 28.0 28.1 13.0 12.3
6 CONCLUSIONS
This paper explores the project cost estimation
process of EPC projects in the dynamic order arrival
situations. Specifically, we develop a heuristic
method that selects orders for cost estimation based
on order selection rules and allocates MH for cost
estimation to each selected order to maximize the
expected profits from orders. The order selection
rules decide bid or no-bid on arrived orders by using
the threshold function MHU
up
(EPPC
i
). This function
is defined through simulation experiments using a
project cost estimation process model proposed based
Case 1.A Case 1.B Case 1.C
MHU basis HEPF
152 161 167
MHU basisi FIFO
151 160 166
No slection HEPF
125 120 111
No selection FIFO
119 109 98
80
100
120
140
160
180
200
220
240
Expected profit [MM$/12 Periods]
Case 2.A Case 2.B Case 2.C
MHU basis HEPF
159 174 186
MHU basisi FIFO
158 171 183
No slection HEPF
151 164 174
No selection FIFO
147 157 166
80
100
120
140
160
180
200
220
240
Expected profit [MM$/12 Periods]
Case 3.A Case 3.B Case 3.C
MHU basis HEPF
176 208 237
MHU basisi FIFO
174 204 233
No slection HEPF
176 207 237
No selection FIFO
173 204 233
80
100
120
140
160
180
200
220
240
Expected profit [MM$/12 Periods]
A Dynamic Scheduling Problem in Cost Estimation Process of EPC Projects
193

on the AACE cost estimate classification system
(AACE, 2011). We analyse the effectiveness of our
heuristic method in terms of the expected profit
through numerical examples.
The following conclusions can be drawn from the
analysis of the numerical examples:
 Our heuristic method developed for the order
selection works well to allocate MH for cost
estimation appropriately so that the expected
profits from orders are maximized in the dynamic
order arrival situations.
 HEPF and FIFO rules, which are used to dispatch
orders waiting for cost estimation, make no
significant difference in the expected profits,
especially when the MHU basis rule is used for
order selection.
There are several issues that require further
research. For example, dispatching rules that
significantly improve the expected profit should be
developed. An advanced procedure to effectively
determine the threshold function MHU
up
(EPPC
i
)
should be devised. In addition, a mechanism that
changes rules of the order selection and MH
allocation dynamically according to the change of
cost estimation conditions, such as order arrival
intervals, order sizes, and so on, should be developed.
In practice, there are dynamic scheduling
problems similar to the project cost estimation
problem, where profitable orders are selected and the
cost estimate class is determined under the conditions
of resource availability. Such examples are sales
activities, facility maintenance activities, and so on.
In these examples, the scope of work and the quality
level of deliverables can be determined dynamically
with limited resources. Research on the project cost
estimation problem can contribute to the development
of management technologies for such problems.
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI Grant
Number 16K01252.
REFERENCES
AACE International, 2011. Cost estimate classification
system – As applied in Engineering, Procurement, and
Construction for the process industries. AACE
International Recommended Practice No. 18R-97.
Bertisen, J., Davis, G. A., 2008. Bias and error in mine
project capital cost estimation. The Engineering
Economist, 53, 118-139.
Humphreys, K. K., 2004. Project and cost engineers’
handbook, CRC Press, Boca Raton.
Ishii, N., Takano, Y., Muraki, M., 2014. An order
acceptance strategy under limited engineering man-
hours for cost estimation in Engineering-Procurement-
Construction projects. International Journal of Project
Management, 32 (3), 519-528.
Ishii, N., Takano, Y., Muraki, M., 2015 (a). A Heuristic
bidding price decision algorithm based on cost
estimation accuracy under limited engineering man-
hours in EPC projects. Simulation and Modeling
Methodologies, Technologies and Applications,
Advances in Intelligent Systems and Computing, 319,
101-118.
Ishii, N., Takano, Y., Muraki, M., 2015 (b). A dynamic
scheduling problem for estimating project cost.
Proceedings of Scheduling Symposium 2015, Tokyo,
119-124.
Jacobs, F. R., Berry, W. L., Whybark, C. D., Vollmann, T.
E., 2011. Manufacturing planning and control for
supply chain management, McGraw-Hill, New York.
Jørgensen, M., Halkjelsvik, T., Kitchenham, B., 2012. How
does project size affect cost estimation error? Statistical
artifacts and methodological challenges, International
Journal of Project Management, 30 (7), 839-849.
Kerzner, H., 2013. Project management: a systems
approach to planning, scheduling, and controlling,
John Wiley & Sons, New Jersey.
Nelson, B. L., Swann, J., Goldsman, D., Song, W., 2001.
Simple procedures for selecting the best simulated
system when the number of alternatives is large,
Operations Research, 49 (6), 950–963.
Oberlender, G. D., Trost, S. M., 2001. Predicting accuracy
of early cost estimates based on estimate quality.
Journal of Construction Engineering and Management,
May/June, 173-182.
Pritchard, N., Scriven, J., 2011. EPC contracts and major
projects. Sweet & Maxwell, London, 2
nd
edition.
Pritsker, A. A. B., O’Reilly, J. J., 1998. AWESIM: The
integrated simulation system. Proceedings of the 1998
Winter Simulation Conference, 249-255.
Shafahi, A., Haghani, A., 2014. Modeling contractors'
project selection and markup decisions influenced by
eminence. International Journal of Project
Management, 32 (8), 1481–1493.
Takano, Y., Ishii N., Muraki, M., 2014. A sequential
competitive bidding strategy considering inaccurate
cost estimates. OMEGA, 42 (1), 132-140.
Takano, Y., Ishii, N., Muraki, M., in press. Multi-Period
resource allocation for estimating project costs in
competitive bidding, Central European Journal of
Operations Research, doi:10.1007/s10100-016-0438-7.
Towler, G., R. Sinnott, R., 2008. Chemical engineering
design principles, practice and economics of plant and
process design, Elsevier, Amsterdam.
Uzzafer, M., 2013. A contingency estimation model for
software projects, International Journal of Project
Management, 31 (7), 981–993.
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
194