Private Multi-party Matrix Multiplication and Trust Computations

∗

Jean-Guillaume Dumas

, Pascal Lafourcade

, Jean-Baptiste Orﬁla

and Maxime Puys

Universit

e Grenoble Alpes, CNRS, LJK, 700 av. Centrale, IMAG - CS 40700, 38058 Grenoble Cedex 9, France

University Clermont Auvergne, LIMOS, Campus Universitaire des C

ezeaux, BP 86, 63172 Aubi

ere Cedex, France

Universit

e Grenoble Alpes, CNRS, Verimag, 700 av. Centrale, IMAG - CS 40700, 38058 Grenoble Cedex 9, France

Keywords:

Secure Multiparty Computation (MPC), Distributed Matrix Multiplication, Trust Evaluation, Proverif.

Abstract:

This paper deals with distributed matrix multiplication. Each player owns only one row of both matrices and

wishes to learn about one distinct row of the product matrix, without revealing its input to the other play-

ers. We ﬁrst improve on a weighted average protocol, in order to securely compute a dot-product with a

quadratic volume of communications and linear number of rounds. We also propose a protocol with ﬁve com-

munication rounds, using a Paillier-like underlying homomorphic public key cryptosystem, which is secure in

the semi-honest model or secure with high probability in the malicious adversary model. Using ProVerif, a

cryptographic protocol veriﬁcation tool, we are able to check the security of the protocol and provide a coun-

termeasure for each attack found by the tool. We also give a randomization method to avoid collusion attacks.

As an application, we show that this protocol enables a distributed and secure evaluation of trust relationships

in a network, for a large class of trust evaluation schemes.

1 INTRODUCTION

Secure multiparty computations (MPC), introduced

by Yao (Yao, 1982) with the millionaires’ problem,

has been intensively studied during the past thirty

years. The idea of MPC is to allow n players to jointly

compute a function f using their private inputs with-

out revealing them. In the end, they only know the

result of the computation and no more information.

Depending on possible corruptions of players, one

may prove that a protocol may resist against a col-

lusion of many players, or that it is secure even if at-

tackers try to maliciously modify their inputs. Mostly

any function can be securely computed (Ben-Or et al.,

1988) and many tools exist to realize MPC proto-

cols. They comprise for instance the use of a Trusted

Third Party (Du and Zhan, 2002), the use of Shamir’s

secret sharing scheme (Shamir, 1979), or more re-

cently the use of homomorphic encryption (Goethals

et al., 2005). It is also possible to mix these tech-

niques (Damg

ard et al., 2012).

Our goal is to apply MPC to the a distributed eval-

∗

This work was partially supported by “Digital trust”

Chair from the University of Auvergne Foundation, by

the HPAC project (ANR 11 BS02 013), the ARAMIS

project (PIA P3342-146798) and the LabEx PERSYVAL-

Lab (ANR-11-LABX-0025).

uation of trust, as deﬁned in (Jøsang, 2007; Dumas

and Hossayni, 2012). There, conﬁdence is a combi-

nation of degrees of trust, distrust and uncertainty be-

tween players. Aggregation of trusts between players

on a network is done by a matrix product deﬁned on

two monoids (one for the addition of trust, the other

one for multiplication, or transitivity): each player

knows one row of the matrix, its partial trust on its

neighbors, and the network as a whole has to com-

pute a distributed matrix squaring. Considering that

the trust of each player for his colleagues is private,

at the end of the computation, nothing but one row of

the global trust has to be learned by each player (i.e.,

nothing about private inputs should be revealed to oth-

ers). Thus, an MPC protocol to resolve this problem

should combine privacy (nothing is learned but the

output), safety (computation of the function does not

reveal anything about inputs) and efﬁciency (Lindell,

2009). First, we need to deﬁne a MPC protocol which

allows us to efﬁciently compute a distributed matrix

product with this division of data between players.

The problem is reduced to the computation of a dot

product between vectors U and V such that one player

knows U and V is divided between all players.

Related Work. Dot product in the MPC model has

been widely studied (Du and Atallah, 2001; Amir-

bekyan and Estivill-Castro, 2007; Wang et al., 2008).

Dumas, J-G., Lafourcade, P., Orﬁla, J-B. and Puys, M.

Private Multi-party Matrix Multiplication and Trust Computations.

DOI: 10.5220/0005957200610072

In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 61-72

ISBN: 978-989-758-196-0

However, in these papers, assumptions made on data

partitions are different: there, each player owns a

complete vector, and the dot product is computed be-

tween two players where; in our setting, trust evalu-

ation should be done among peers, like certiﬁcation

authorities. For instance, using a trusted third party

or permuting the coefﬁcients is unrealistic. Now,

computing a dot product with n players is actually

close to the MPWP protocol of (Dolev et al., 2010),

computing a mean in a distributed manner: comput-

ing dot products is actually similar to computing a

weighted average where the weights are in the known

row, and the values to be averaged are privately dis-

tributed. In MPWP the total volume of communica-

tion for a dot product is O





with O (n) commu-

nication rounds. Other generic MPC protocols ex-

ist, also evaluating circuits, they however also require





computations and/or communications per dot-

product (Bendlin et al., 2011; Damg

ard et al., 2012).

Contributions. We provide the following results:

• A protocol P-MPWP, improving on MPWP,

which reduces both the computational cost, by al-

lowing the use of Paillier’s cryptosystem, and the

communication cost, from O





to O





• An O (n) time and communications protocol Dis-

tributed and Secure Dot-Product (DSDP

) (for i

participants) which allows us to securely compute

a dot product UV , against a semi-honest adver-

sary, where one player owns a vector U and where

each player knows one coefﬁcient of V .

• A parallel variant that performs the dot-product

computation in parallel among the players, lim-

its the total number of rounds. This is extended

to a Parallel Distributed and Secure Matrix-

Multiplication (PDSMM

) family of protocols.

• A security analysis of the DSDP protocol using

a cryptographic protocol veriﬁcation tool, here

ProVerif (Blanchet, 2001; Blanchet, 2004). This

tool allows us to deﬁne countermeasures for each

found attack: adapted proofs of knowledge in or-

der to preserve privacy and a random ring order,

where private inputs are protected as in a wiretap

code (Ozarow and Wyner, 1984) and where the

players take random order in the protocol to pre-

serve privacy with high probability, even against a

coalition of malicious insiders.

• Finally, we show how to use these protocols for

the computation of trust aggregation, where clas-

sic addition and multiplication are replaced by

more generic operations, deﬁned on monoids.

In Section 2, we thus ﬁrst recall some multi-party

computation notions. We then introduce in Section 3

the trust model based on monoids. In Section 4, we

present our quadratic variant of MPWP and a linear-

time protocol in Section 5. We then give the asso-

ciated security proofs and countermeasures in Sec-

tion 6 and present parallelized version in Section 7.

Finally, in Section 8, we show how our protocols can

be adapted to perform a private multi-party trust com-

putation in a network.

2 BACKGROUND

We use a public-key homomorphic encryption

scheme where both addition and multiplication are

considered. There exist many homomorphic cryp-

tosystems, see for instance (Mohassel, 2011, § 3)

and references therein. We need the following

properties on the encryption function E (accord-

ing to the context, we use E

PubB

, or E

or just

E to denote the encryption function, similarly for

the signature function, D

or D

privB

): computing

several modular additions, denoted by Add(c

on ciphered messages and one modular multipli-

cation, denoted by Mul(c;m), between a ciphered

message and a cleartext. That is, ∀m

∈

Z/mZ: Add(E(m

);E(m

)) = E(m

+ m

mod m)

and Mul(E(m

);m

) = E(m

mod m). For in-

stance, Paillier’s or Benaloh’s cryptosystems (Pail-

lier, 1999; Benaloh, 1994; Fousse et al., 2011)

can satisfy these requirements, via multiplication

in the ground ring for addition of enciphered mes-

sages (Add(E(m

);E(m

)) = E(m

)E(m

) mod m),

and via exponentiation for ciphered multiplication

(Mul(E(m

);m

) = E(m

)

mod m), we obtain the

following homomorphic properties:

E(m

)E(m

) = E(m

+ m

mod m) (1)

E(m

)

= E(m

mod m) (2)

Since we consider the semantic security of the

cryptosystem, we assume that adversaries are prob-

abilistic polynomial time machines. In MPC, most

represented intruders are the following ones:

• Semi-honest (honest-but-curious) Adversaries: a

corrupted player follows the protocol speciﬁca-

tions, but also tries to gather as many information

as possible in order to deduce some private inputs.

• Malicious Adversaries: a corrupted player that

controls the network and stops, forges or listens

to messages in order to gain information.

3 MONOIDS OF TRUST

There are several schemes for evaluating the transitive

trust in a network. Some use a single value represent-

SECRYPT 2016 - International Conference on Security and Cryptography

ing the probability that the expected action will hap-

pen; the complementary probability being an uncer-

tainty on the trust. Others include the distrust degree

indicating the probability that the opposite of the ex-

pected action will happen (Guha et al., 2004). More

complete schemes can be introduced to evaluate trust:

Jøsang introduces the Subjective Logic notion which

expresses beliefs about the truth of propositions with

degrees of ”uncertainty” in (Jøsang, 2007). Then the

authors of (Huang and Nicol, 2010) applied the asso-

ciated calculus of trust to public key infrastructures.

There, trust is represented by a triplet, (trust, dis-

trust, uncertainty) for the proportion of experiences

proved, or believed, positive; the proportion of expe-

riences proved negative; and the proportion of expe-

riences with unknown character. As uncertainty =

1−trust −distrust, it is sufﬁcient to express trust with

two values as htrust,distrusti. In e.g. (Foley et al.,

2010) algorithms are proposed to quantify the trust

relationship between two entities in a network, using

transitivity and reachability. For instance, in (Dumas

and Hossayni, 2012) the authors use an adapted power

of the adjacency matrix to evaluate the trust using

all existing (ﬁnite) trust paths between entities. We

show in the following of this section, that powers of

this adjacency matrix can be evaluated privately in a

distributed manner, provided than one disposes of an

homomorphic cryptosystem satisfying the homomor-

phic Properties (1) and (2).

3.1 Aggregation of Trust

Consider Alice trusting Bob with a certain trust de-

gree, and Bob trusting Charlie with a certain trust de-

gree. The sequential aggregation of trust formalizes

a kind of transitivity to help Alice to make a decision

about Charlie, that is based on Bob’s opinion. In the

following, we ﬁrst consider that the trust values are

given as a pair ha, bi ∈ D

, for D a principal ideal ring:

for three players P

, P

and P

, where P

trusts P

with

trust value ha,bi ∈ D

and P

trusts P

with trust value

hc,di ∈ D

the associated sequential aggregation of

trust is a function F : D

× D

→ D

, that computes

the trust value over the trust path P

ha,bi

→ P

hc,di

→ P

as ha, biFhc,di = hac + bd,ad + bci. Similarly, from

Alice to Charlie, there might be several ways to per-

form a sequential aggregation (several paths with ex-

isting trust values). Therefore it is also possible to

aggregate these parallel paths with the same mea-

sure, in the following way: for two disjoint paths

ha,bi

→ P

and P

hc,di

→ P

, the associated parallel ag-

gregation of trust is a function z : D

×D

→ D

, that

computes the resulting trust value as: ha,bizhc,di =

ha + c − ac,bdi. We prove the following Lemma.

Lemma 1. ha,bi is invertible for z if and only if (b

is invertible in D) and (a = 0 or a − 1 is invertible).

Proof. As ha + 0 − a.0, b.1i=ha,bi, h0,1i is neutral

for z. Then, for b invertible, if a = 0, then h0,b

−1

i is

an inverse for h0,bi. Otherwise, for a − 1 invertible,

ha(a − 1)

−1

izha,bi = ha,bizha(a − 1)

−1

= ha + a(a − 1)

−1

− a

(a − 1)

−1

,bb

−1

i = h0,1i.

Similarly, if ha,bizhc,di = h0,1i, then bd = 1 and b

is invertible. Then also (a − 1)c = a. Finally if a 6= 0

and a − 1 is a zero divisor, there exists λ 6= 0 such

that λ(a − 1) = 0, thus λ(a − 1)c = 0 = λa, but then

λ(a − 1) − λa = −λ = 0. As this is contradictory, the

only possibilities are a = 0 or a − 1 invertible.

3.2 Multi-party Private Aggregation

For E an encryption function, we deﬁne the natural

morphism on pairs, so that it can be applied to trust

values: E(ha,bi) = hE(a),E(b)i.We can thus extend

homomorphic properties to pairs so that the parallel

and sequential aggregation can then be computed ho-

momorphically, provided that one entry is in clear.

Lemma 2. With an encryption function E, satisfying

the homomorphic Properties (1) and (2), we have:

Mul(E (ha,bi); hc,di) = E (ha,biFhc,di)

= hE(a)

E(b)

,E(a)

E(b)

Add(E (ha,bi); hc,di) = E (ha,bizhc,di)

= hE(a)E(c)E(a)

−c

,E(b)

Moreover, those two functions can be computed on an

enciphered ha,bi, provided that hc,di is in clear.

Proof. From the homomorphic properties of the en-

cryption functions, we have: E(a)

E(b)

= E(ac +

bd), E(a)

E(b)

= E(ad + bc), E(a)E(c)E(a)

−c

E(a+c+a(−c)) and E(b)

= E(bd). For the compu-

tation, both right hand sides depend only on ciphered

values E(a), E(b), and on clear values c and d (E(c)

can be computed with the public key, from c).

This shows, that in order to compute the aggre-

gation of trust privately, the ﬁrst step is to be able to

compute dot-products privately.

4 FROM MPWP TO P-MPWP

4.1 MPWP Description

The MPWP protocol (Dolev et al., 2010) is used to

securely compute private trust values in an additive

reputation system between n players. Each player

Private Multi-party Matrix Multiplication and Trust Computations

(excepted P

, assumed to be the master player)

has a private entry v

, and P

private entries are

weights u

associated to others players. The goal is

to compute a weighted average trust, i.e.,

∑

i=2

∗ v

The idea of MPWP is the following: the ﬁrst player

creates a vector TV containing her private entries

ciphered with her own public key using Benaloh’s

cryptosystem, i.e., TV = [E

),. ..,E

)]. Then,

also sends a (n − 1) × (n − 1) matrix M, with

all coefﬁcients initialized to 1 and a variable A = 1.

Once (M,TV,A) received, each player computes:

A = A ∗ E

)

∗ E

), where z

is a random value

generated by P

. At the end, the ﬁrst player gets

(A) =

∑

i=2

+ z

. Then, the idea is to cut the z

values in n −1 positive shares such that z

∑

j=2

i, j

Next, each z

i, j

is ciphered with the public key of P

the result is stored into the i

column of M, and M is

forwarded to the next player. In a second phase, play-

ers securely remove the added random values to A,

from M = (m

i, j

) = (E

i, j

)): each player P

, except

, computes her PSS

∑

i=2

i, j

) =

∑

i=2

i, j

by deciphering all values contained in the j

row

of M; then they send γ

= E

(PSS

) to P

, their

PSS

ciphered with the public key of P

. At the

end, P

retrieves the result by computing Trust =

(A) −

∑

j=2

(γ

) = D

(A) −

∑

j=2

PSS

(A) −

∑

j=2

∑

i=2

i, j

= D

(A) −

∑

i=2

∑

i=2

4.2 P-MPWP: A lighter MPWP

P-MPWP is a variant of MPWP with two main differ-

ences: ﬁrst Paillier’s cryptosystem is used instead of

Benaloh’s, and, second, the overall communications

cost is reduced from O





to O





by sending parts

of the matrix only. All steps of P-MPWP but those

clearly identiﬁed in the following are common with

MPWP, including the players’ global settings. Since

P-MPWP is using a cryptosystem where players can

have different modulus, some requirements must be

veriﬁed in the players’ settings. First of all, a bound B

needs to be ﬁxed for the vectors’ private coefﬁcients:

∀i,0 ≤ u

≤ B,0 ≤ v

≤ B (3)

With Benaloh, the common modulus M must be

greater than the dot product, thus at most:

(n − 1)B

< M. (4)

Differently, with Paillier, each player P

has a differ-

ent modulus N

. Then, by following the MPW P pro-

tocol steps, at the end of the ﬁrst round, P

obtains

A =

∏

i=2

)

∗ E

). In order to correctly de-

cipher this coefﬁcient, if the players’ values, as well

as their random values z

, satisfy the bound (3), her

modulo N

must be greater than (n − 1)(B

+ B). For

others players, there is only one deciphering step, at

the second round. They received (n − 1) shares all

bounded by B. Hence, their modulus N

need only be

greater than (n − 1)B. These modulus requirements

are summarized in the following lemma:

Lemma 3. Let n > 3 be the number of players. Under

the bound (3), if ∀i,0 ≤ z

≤ B and if also the modulus

satisfy (n − 1)(B

+ B) < N

and (n − 1)B < N

, ∀i =

2,...,n, then at the end of P-MPWP, P

obtains S

∑

i=2

∗ v

Now, the reduction of the communications cost in

P-MPWP, is made by removing the exchange of the

full M matrix between players. At the z

i, j

shares com-

putation, each P

directly sends the j

coefﬁcient to

the j

player instead of storing results in T . In the

end, each player P

receives (n − 1) values ciphered

with his public key, and he can compute the PSS

deciphering and adding each received values, exactly

as in MPW P. Thus, each player sends only O (n) val-

ues, instead of O





. All remaining steps can be

executed as in MPWP.

Both Paillier’s and Benaloh’s cryptosystems pro-

vides semantic security, thus the security of P-MPWP

is not altered. Moreover, since a common bound is

ﬁxed a priori on private inputs, P-MPWP security can

be reduced to the one in MPWP with the common

modulo M between all players (Michalas et al., 2012).

Finally, since all exploitable (i.e., clear or ciphered

with the dedicated key) information exchanged rep-

resents a subset of the MPWP players’ knowledge, if

one is able to break P-MPWP privacy, then one is also

able to break it in MPWP.

5 A LINEAR DOT PRODUCT

PROTOCOL

5.1 Overview with Three Players

We ﬁrst present in Figure 1 our DSDP

protocol (Dis-

tributed and Secure Dot-Product), for 3 players. The

idea is that Alice is interested in computing a dimen-

sion 3 dot-product S = u

· v, between her vector u

and a vector v whose coefﬁcients are owned by dif-

ferent players. The other players send their coefﬁ-

cients, encrypted, to Alice. Then she homomorphi-

cally multiplies each one of these by her u

coefﬁ-

cients and masks the obtained u

by a random value

. Then the other players can decrypt the resulting

+ r

: with two unknowns u

and r

they are not

able to recover v

. Finally the players enter a ring

computation of the overall sum before sending it to

Alice. Then only, Alice removes her random masks

SECRYPT 2016 - International Conference on Security and Cryptography

to recover the ﬁnal dot-product. Since at least two

players have added u

+ u

, there is at least two

unknowns for Alice, but a single equation.

We need that after several decryptions and

re-encryptions, and removal of the random val-

ues r

, S is exactly

∑

. The homomor-

phic Properties (1) and (2) only guaranty that

D(Add(Mul(E(v

);u

);r

)) = v

+ r

mod N

, for

the modulo N

of the cryptosystem used by player P

But then these values must be re-encrypted with an-

other player’s cryptosystem, potentially with another

modulo. Finally Alice also must be able to remove

the random values and recover S over Z. On the one

hand, if players can share the same modulo M = N

for the homomorphic properties then decryptions and

re-encryptions are naturally compatible. This is pos-

sible for instance in Benaloh’s cipher. On the other

hand, in a Paillier-like cipher, at the end of the pro-

tocol, Alice will actually recover S

= ((u

+ r

)

mod N

+ u

+ r

) mod N

. He can remove r

via S

= S

− r

mod N

, but then S

= ((u

+ r

)

mod N

) mod N

. Now, if vectors coefﬁcients

are bounded by say B, and if the third modulo is

larger than the second, N

> N

+ B

, the obtained

value is actually the exact value over the naturals:

= (u

+ r

) mod N

+ u

. Then Alice can re-

move the second random value, this time modulo N

= (u

+ u

) mod N

, where now N

> 2B

sufﬁces to recover S = S

∈ N. We generalize this

in the following section.

5.2 General Protocol with n Players

We give the generalization DSDP

, of the protocol of

Figure 1 for n players in Algorithm 1 hereafter. For

this protocol to be correct, we use the previously de-

ﬁned bound (3) on the players’ private inputs. Then,

for n players, there are two general cases: First, if all

the players share the same modulo M = N

for all i

for the homomorphic properties, then Alice can also

use M to remove the r

. Then, to compute the correct

value S, it is sufﬁcient to satisfy the bound (4). Sec-

ond, for a Paillier-like cipher, differently, the modulo

of the homomorphic properties are distinct. We thus

prove the following Lemma 4.

Lemma 4. Under the bound (3), and for any r

, let

= (u

) mod N

and M

= (M

i−1

)

mod N

, for i = 2 ...n − 1. Let also S

n+1

= M

and

= (S

i+1

− r

) mod N

for i = n...2. If we have:

(

i−1

+ (n − i + 1)B

< N

, for all i = 3..n

(n − 1)B

< N

(5)

then S

∑

i=2

∈ N.

Algorithm 1: DSDP

Protocol: Distributed and Secure Dot-

Product of size n.

Require: n ≥ 3 players, two vectors U and V such

that P

knows complete vector U, and each play-

ers P

knows component v

of V , for i = 1...n;

Require: E

(resp. D

), encryption (resp. decryption)

function of P

, for i = 2...n.

Ensure: P

knows the dot-product S = U

V .

1: for i = 2 .. .n do {P

: c

= E

); P

→ P

}

2: for i = 2 .. .n do

3: P

: r

← Z/N

4: P

: α

= c

∗ E

) so that α

= E

+ r

)

5: P

→ P

6: for i = 2 .. .n − 1 do P

i+1

→ P

7: P

: ∆

= D

(α

) so that ∆

= u

+ r

8: P

: β

= α

∗E

(∆

) so that β

= E

∆

); P

→ P

9: for i = 3 .. .n − 1 do

10: P

: ∆

= D

(β

) so that ∆

∑

k=2

+ r

11: P

: β

i+1

= α

i+1

∗ E

i+1

(∆

) so that β

i+1

+ r

i+1

+ ∆

); P

i+1

→ P

i+1

12: P

: ∆

= D

(β

); P

: γ = E

(∆

); P

→ P

13: return P

: S = D

(γ) −

∑

n−1

i=1

+ u

Proof. By induction, we ﬁrst show that S

= M

i−1

∑

j=i

, for i = n..3: indeed S

= (M

− r

)

mod N

= (M

n−1

+ u

) mod N

. But M

n−1

modulo N

n−1

, so (M

n−1

+ u

) < N

n−1

+ B

, and

then (5) for i = n, ensures that N

n−1

+ B

< N

and S

= M

n−1

+ u

∈ N. Then, for 3 ≤ i <

n, S

= (S

i+1

− r

) mod N

= (M

∑

j=i+1

−

) mod N

= (M

i−1

+ u

+ r

∑

j=i+1

− r

)

mod N

= (M

i−1

∑

j=i

) mod N

, by induction.

But (3) enforces that M

i−1

∑

j=i

< N

i−1

+ (n −

i + 1)B

and (5) also ensures the latter is lower than

. Therefore S

= M

i−1

∑

j=i

and the induction

is proven. Finally, S

= (S

− r

) mod N

= (M

∑

j=3

− r

) mod N

= (

∑

j=2

) mod N

. As

∑

j=2

< (n − 1)B

, by (5) for i = 2, we have

∑

j=2

∈ N.

This shows that the DSDP

protocol of Algo-

rithm 1 can be implemented with a Paillier-like un-

derlying cryptosystem, provided that the successive

players have increasing modulo for their public keys.

Theorem 1. Under the bounds (3), and under Hy-

pothesis (4) with a shared modulus underlying cipher,

or under Hypothesis (5) with a Paillier-like underly-

ing cipher, the DSDP

protocol of Algorithm 1 is cor-

rect. It requires O (n) communications and O (n) en-

cryption and decryption operations.

Private Multi-party Matrix Multiplication and Trust Computations

Alice (P1) Bob (P2) Charlie (P3)

= E

pubB

) c

= E

pubC

)

= c

∗ E

pubB

)

= c

∗ E

pubC

)

, α

∆

= D

privB

(α

) {now ∆

is (v

+ r

)}

= α

∗ E

pubC

(∆

)

∆

= D

privC

(β

)

{now ∆

is (v

+ r

) +(v

+ r

)}

γ = E

pubA

(∆

)

S = D

privA

(γ) −r

− r

+ u

{now S is u

+ u

}

Figure 1: DSDP

: Secure dot product of vectors of size 3 with a Paillier-like asymmetric cipher.

Proof. First, each player sends his ciphered entry

to P

, then homomorphically added to random val-

ues, r

. Then, P

(i ≥ 2) deciphers the message re-

ceived by P

i−1

into ∆

. By induction, we obtain

∆

∑

k=2

+ r

. This value is then re-enciphered

with next player’s key and the next player share is ho-

momorphically added. Finally, P

just has to remove

all the added randomness to obtain S = ∆

−

∑

i=2

∑

i=1

. For the complexity, the protocol

needs n − 1 encryptions and communications for the

; 2(n − 1) homomorphic operations on ciphers and

n − 1 communications for the α

; n − 1 decryptions

for the ∆

; n − 1 encryptions, homomorphic opera-

tions and communications for the β

; and ﬁnally one

encryption and one communication for γ. Then P

needs O (n) operations to recover S.

6 SECURITY OF DSDP

We study the security of DSDP

using both mathe-

matical proofs and automated veriﬁcations. We ﬁrst

demonstrate the security of the protocol for semi-

honest adversaries. Then we incrementally build its

security helped by attacks found by ProVerif, an au-

tomatic veriﬁcation tool for cryptographic protocols.

6.1 Security Proofs

The standard security deﬁnition in MPC models (Lin-

dell, 2009) covers actually many security issues, such

as correctness, inputs independence, privacy, etc. We

ﬁrst prove that under this settings, computation of the

dot product is safe.

Lemma 5. For n ≥ 3, the output obtained after com-

puting a dot product where one player owns complete

vector U, and where each coefﬁcient v

of the second

vector V is owned by the player P

, is safe.

Proof. After executing DSDP

with n ≥ 3, P

re-

ceived the dot product of U and V . Therefore, it owns

only one equation containing (n −1) unknown values

(coefﬁcients from v

to v

). Then, he cannot deduce

other players’ private inputs.

Then, proving the security relies on a comparison

between a real-world protocol execution and an ideal

one. The latter involves an hypothetical trusted third

party (T T P) which, knowing only the players’ private

inputs, returns the correct result to the correct play-

ers. The protocol is considered secure if the players’

views in the ideal case cannot be distinguished from

the real ones. Views of a player P

(denoted View

)

are deﬁned as distributions containing: the players’

inputs (including random values), the messages re-

ceived during a protocol execution and the outputs.

The construction of the corrupted players’ view in the

ideal world is made by an algorithm called Simulator.

Deﬁnition 1. In the presence of a set C of semi-honest

adversaries with inputs set X

, a protocol Π securely

computes f : ([0, 1]

∗

)

→ ([0,1]

∗

)

(and f

denotes

the outputs of f for each adversaries in C) if there

exists a probabilistic polynomial-time algorithm Sim,

such that: {Sim(C,{X

}, f

(X))}

X∈([0,1]

∗

)

is compu-

tationally indistinguishable from {C,{View

}

∈C

For DSDP

, it is secure only if C is reduced to a

singleton, i.e. if only one player is corrupted.

Lemma 6. By assuming the semantic security of the

cryptosystem E, for n ≥ 3, DSPD

is secure against

one semi-honest adversary.

SECRYPT 2016 - International Conference on Security and Cryptography

Proof. We assume that the underlying cryptosys-

tem E is semantically secure (IND-CPA secure).

First, we suppose that only P

is corrupted. His

view, in a real execution of the protocol, is

View

= {U, R,γ,S, A,B,C}, where U = {u

}

1≤i≤n

R = {r

}

1≤i≤n

, A = {α

}

2≤i≤n

, B = {β

}

3≤i≤n−1

and

C = {c

}

2≤i≤n

. Now, Sim

is the simulator for P

in the ideal case, where a simulated value x is de-

noted x

: by deﬁnition, P

’s private entries (vectors

U and R) are directly accessible to Sim

, along with

the output S, sent by the T T P. Sim

starts by gen-

erating n − 2 random values, and then ciphers them

using the corresponding public keys: this simulates

the c

values. Then, using the provided r

and u

with the associated c

and P

’s public key, Sim

com-

putes: α

= c

∗ E

),2 ≤ i ≤ n. Next, the sim-

ulation of B

is done by ciphering random values

with the appropriate public key. The γ

value is

computed using R along with the protocol output S:

= E

(S +

∑

n−2

+ u

). In the end, the simulator

view is View

Sim

= {U, R,γ

,S,A

}. If an adver-

sary is able to distinguish any ciphered values (e.g.

from C and thus A

from A), hence he is able to

break the semantic security of the underlying crypto-

graphic protocol. This is assumed impossible. More-

over, since the remaining values are computed as in

a real execution, P

is not able to distinguish View

from View

Sim

. Second, we suppose that a player

,i ≥ 2 is corrupted and denote by Sim

the simulator

in this case. Since the role played by each participant

is generic, (except for P

, which only differs by his

computation of γ instead of β

n+1

), the simulators are

easily adaptable. During a real protocol execution, the

view of P

is View

= {v

,A,B,C,γ,∆

}. Simulating

the values also known to P

is similar, up to the used

keys. Hence, the simulation of A

, B

, γ

, C

(except

) is made by ciphering random values using the ade-

quate public key. c

is ciphered using v

and the public

key of P

. For ∆

, the simulator Sim

has to forward the

random value previously chosen to be ciphered as α

Indistinguishability is based on the semantic security

of E (for A, B, C and γ) and on the randomness added

by P

(and thus unknown by P

). Then, ∆

is compu-

tationally indistinguishable from the real ∆

. Hence,

View

and View

are indistinguishable and DSDP

secure against one semi-honest adversary.

6.2 Automated Veriﬁcation

Alongside mathematical proofs, we use an auto-

matic protocol veriﬁcation tool to analyze the secu-

rity of the protocol. Among existing tools, we use

ProVerif (Blanchet, 2001; Blanchet, 2004). It allows

users to add their own equational theories to model a

large class of protocols. In our case, we model prop-

erties of the underlying cryptosystem including addi-

tion and multiplication. Sadly, veriﬁcation of proto-

col in presence of homomorphic function over abelian

groups theory has been proven undecidable (Delaune,

2006). Moreover, as showed in (Lafourcade and Puys,

2015), some equational theories such as Exclusive-Or

can already outspace the tool’s capacities. Thus we

have to provide adapted equational theories to be able

to obtain results with the tool. We modeled the appli-

cation of Pailler’s or shared modulus encryption prop-

erties on α

messages that Bob receives as follows:

(i). ∀u,v, r, k, bob(E

(r), u,E

(v)) = E

(uv + r)

This property allows Bob to obtain u

from α

This also allows an intruder to simulate such calculus

and impersonate Bob. We also model:

(ii). β

by ∀u,v,r,x,y,z,k, charlie(E

(uv +

r), E

(xy + z)) = E

(uv + xy + r + z)

(iii). β

by ∀u,v, r, x,y,z, a,b,c,k, dave(E

(uv + xy +

r + z),E

(ab + c)) = E

(uv + xy + ab + r + z + c)

In the following, we use ProVerif to prove the secu-

rity of our protocols under the abstraction of the func-

tionalities given in our equational theory. ProVerif

discovers some attacks in presence of active intruder.

We then propose some countermeasures. The lim-

its of ProVerif are reached and it does not terminate.

The associated source ﬁles are available in a web-site:

http://matmuldistrib.forge.imag.fr

Analysis in Case of a Passive Adversary. Using

these equational theories on the protocol described

in Figure 1, we verify it in presence of a passive in-

truder. Such adversary is able to observe all the trafﬁc

of the protocol and tries to deduce secret information

of the messages. This corresponds to a ProVerif in-

truder that only listens to the network and does not

send any message. By default, this intruder does not

possess the private key of any agent and thus does not

belong to the protocol. To model a semi-honest adver-

sary as deﬁned in Section 2, we just give secret keys

of honest participants to the passive intruder knowl-

edge in ProVerif. Then the tool proves that all secret

terms cannot be learn by the intruder for any combi-

nations of leaked key. This conﬁrms the proofs given

in Section 6.1 against the semi-honest adversaries.

Analysis in Case of Malicious Adversary. The

malicious adversary described in Section 2 is an ac-

tive intruder that controls the network and knows

a private key of a compromised honest participant.

Modeling this adversary in ProVerif, we are able to

spot the two following attacks and give some counter-

measures:

Private Multi-party Matrix Multiplication and Trust Computations

Intruder(Alice) Bob Charlie

pubB

)

= c

∗ E

pubB

)

= E

pubC

)

= x

∗ E

pubC

)

,α

∆

= D

privB

(α

) {now ∆

is (v

+ r

)}

=α

∗E

pubC

(∆

)

∆

= D

privC

(β

)

{now ∆

is (v

+ r

) + (v

+ r

)}

γ=E

pubA

(∆

)

= (D

privA

(γ) − v

− r

−1

Figure 2: Attack on the secrecy of v

(i) Only the key of Alice is compromised and the

countermeasure uses proofs of knowledge.

(ii) Only the key of Charlie is compromised and the

countermeasure uses signatures.

In the rest of the section, we present these two points.

In the Section 7.2, we also give a solution called ran-

dom ring for the case where both keys of Alice and

Charlie are compromised.

(i) The key of Alice is compromised. An attack on

the secrecy of v

, the secret generated by Bob, is then

presented in Figure 2.

The malicious adversary usurps Alice and re-

places all the α

messages, arriving from the other

agents, with one message she generated, except one

message, denoted c

in Figure 2. He lets the proto-

col end normally and obtains a term where only v

unknown. He learns v

. If the key of Alice (P

) is

compromised, ProVerif also ﬁnds an attack on any of

the other players secrecy. Suppose, w.l.o.g, that P

the target, P

replaces each α

except α

by ciphers

) where x

are known to him. x

= 0 could do for

instance (x

= 0v

+ r

also), since after completion of

the protocol, P

learns u

+ r

∑

i=3

, where the

and r

are known to him. Therefore, P

learns v

Note also that similarly, for instance, α

= 1v

+0 and

= v

could also reveal v

to P

. Counter measure:

this attack, and more generally attacks on the form of

the α

can be counteracted by zero-knowledge proofs

of knowledge. P

has to prove to the other players

that α

is a non trivial afﬁne transform of their secret

. For this we use a variant of a proof of knowledge

of a discrete logarithm (Chaum et al., 1986) given in

Figure 3.

In the Protocol 1, this proof of a non trivial afﬁne

transform applies as is to α

with µ

= g

, ρ

= g

that the check of P

is δ

= g

∆

== µ

. Differently,

for the subsequent players, the δ

i−1

= g

∆

i−1

used to

test must be forwarded: indeed the subsequent play-

ers have to check in line 10 that ∆

= u

+ r

+ ∆

i−1

Alice Public: g Bob

c = E

pubB

(v)

α = E

pubB

(uv +r)

µ = g

and ρ = g

α, µ, ρ

Check µ 6= 1, µ 6= g so that u 6= 0,u 6= 1

Check ρ 6= 1, ρ 6= g so that r 6= 0,r 6= 1

∆ = D

privB

(α) if ∆ = uv +r

Check g

∆

== µ

ρ then g

uv+r

= (g

)

Figure 3: Proof of a non trivial afﬁne transform.

Thus with P

providing µ

= g

, ρ

= g

and P

i−1

providing δ

i−1

, the check of player P

ends with δ

∆

== µ

i−1

. As for proofs of knowledge of dis-

crete logarithm, secrecy of our proof of non trivial

afﬁne transform is guaranteed as long as the discrete

logarithm is difﬁcult. The overhead in the protocol,

in terms of communications, is to triple the size of the

messages from P

to P

, with α

growing to (α

,µ

,ρ

and to double the size of the messages from P

to P

i+1

with β

growing to (β

,δ

). In terms of computations,

it is also a neglectible linear global overhead.

(ii) The key of Charlie is compromised. There

ProVerif ﬁnds another attack on the secrecy of v

This time the key of Charlie is compromised and

the malicious adversary blocks all communications to

and from Alice who is honest. The adversary per-

forms the same manipulation on the α

terms which

are directly sent to Bob. Thus, this attack becomes

feasible since the adversary knows the terms u

, u

, r

and v

that he generated and ∆

= (v

+ r

) using the private key of Charlie. Such an

attack relies on the fact that Bob has no way to ver-

ify if the message he receives from Alice has really

been sent by Alice. This can be avoided using crypto-

graphic signatures.

This attack can be generalized to any number of

participants. The attack needs the adversary to know

the key of Alice (since she is the only one to know

the u

and r

values thanks to the signatures). Then, to

obtain the secret value of a participant P

, the key of

participants P

i−1

and P

i+1

are also needed:

(i). P

i−1

knows ∆

i−1

= (u

+ ... + u

i−1

+ r

... + r

i−1

(ii). P

i+1

knows ∆

i+1

= (u

+... +u

i−1

i+1

+ r

+ ... + r

i−1

+ r

i+1

Thus, by simplifying ∆

i−1

and ∆

i+1

, the malicious

adversary obtains u

+ u

i+1

+ r

i+1

where he

can remove u

i+1

, v

i+1

, r

i+1

and u

to obtain v

. For

more than three participants, we see in Section 7.2

that these kinds of threats can be diminished if the

protocol is replayed several times in random orders.

SECRYPT 2016 - International Conference on Security and Cryptography

7 PARALLEL APPROACH

In order to speed up the overall process, we show that

we can cut each dot-product into blocks of 2 or 3 co-

efﬁcients. On the one hand, the overall volume of

communications is unchanged, while the number of

rounds is reduced from n to a maximum of 5. On the

other hand, semantic security is dropped, but we will

see at the end of this section that by simply repeating

the protocol with a wiretap mask it is possible to make

the probability of breaking the protocol negligible.

An application of the DSDP

protocol is the com-

putation of matrix multiplication. In this case, instead

of knowing one vector, each player P

owns two rows,

and B

, one of each n × n matrices A and B. At

the end, each P

learns a row C

of the matrix C = AB.

In order to compute the matrix product, it is therefore

natural to parallelize DSDP

: each dot-product is cut

into blocks of 2 or 3 coefﬁcients. Indeed, scalar prod-

uct between three players (resp. four) involves two

(resp. three) new coefﬁcients in addition to the ones

already known by P

. For P

, the idea is to call DSDP

on the coefﬁcients u

and u

of P

, and v

and P

. Then P

knows s = u

+ u

. P

can then continue the protocol with P

and P

, using

(s,1) as his ﬁrst coefﬁcient and u

to be combined

with v

, etc. P

can also launch the computations

in parallel. Then P

adds his share u

only after all

the computations. For this it is sufﬁcient to modify

line 13 of DSDP

as: P

: S = D

(γ)−

∑

n−1

i=1

. This is

given as the ESDP

protocol variant in Algorithm 2.

Algorithm 2: ESDP

Protocol: External Secure Dot-Product

of size n.

Require: n +1 players, P

knows a coefﬁcient vector

U ∈ F

, each P

knows components v

i−1

of V ∈ F

for i = 2...n + 1.

Ensure: P

knows S = U

V .

return DSDP

n+1

...P

n+1

,[0,U],[0,V ]).

7.1 Partition in Pairs or Triples

Depending on the parity of n, and since gcd(2, 3) = 1,

calls to ESDP

and ESDP

are sufﬁcient to cover

all possible dot-product cases, as shown in protocol

PDSMM

of Algorithm 3. The protocol is cut in two

parts. The loop allows us to go all over coefﬁcients by

block of size 2. In the case where n is even, a block

of 3 coefﬁcients is treated with an instance of ESDP

In terms of efﬁciency and depending on the parity of

n, ESDP

is called

n−1

− 2 times, and ESDP

called 0 or 1 times.

Algorithm 3: PDSMM

Protocol: Parallel Distributed and

Secure Matrix Multiplication.

Require: n players, each player P

knows rows A

and B

of two n × n matrices A, B.

Ensure: Each player P

knows row i of C = AB.

1: for Each row: i=1 . . . n do

2: for Each column: j=1 . . . n do

3: s ← a

i,i

i, j

4: if n is even then

5: k

← (i − 1) mod n + 1; k

← (i − 2)

mod n + 1; k

← (i − 3) mod n + 1;

6: s ← s + ESDP

, [P

i,k

], [b

, j

])

7: t ←

n−4

8: else

9: t ←

n−1

10: for h = 1...t do

11: k

← (i + 2h − 1) mod n + 1; k

← (i +

2h) mod n + 1;

12: s ← s + ESDP

, [P

], [a

i,k

, j

])

13: c

i, j

← s

Theorem 2. The PDSMM

Protocol in Algorithm 3 is

correct. It runs in less than 5 parallel communication

rounds.

Proof. Correctness means that at the end, each P

has

learnt row C

of C = AB. Since the protocol is ap-

plied on each rows and columns, let us show that

for a row i and a column j, Algorithm 3 gives the

coefﬁcient c

i j

such that c

i j

∑

k=1

∗ b

k j

. First,

the k

coefﬁcients are just the values 1. ..(i − 1) and

(i + 1)...n in order. Then, the result of any ESDP

step is a

i,k

, j

+ a

i,k

, j

and the result of the po-

tential ESDP

step is a

i,k

, j

+ a

i,k

, j

+ a

i,k

, j

Therefore accumulating them in addition of a

i,i

∗ b

i, j

produces as expected c

i j

∑

k=1

∗ b

k j

Now for the number of rounds, for all i and j, all

the ESDP calls are independent. Therefore, if each

player can simultaneously send and receive multiple

data we have that: in parallel, ESDP

, like DSDP

Figure 1, requires 4 rounds with a constant number

of operations: one round for the c

, one round for the

, one round for β

and one round for γ. As shown

in Algorithm 1, ESDP

, like DSDP

, requires only a

single additional round for β

7.2 Random Ring Order Mitigation

We have previously seen that if the ﬁrst player of a

dot-product cooperates with the third one she can al-

ways recover the second player private value. If the

Private Multi-party Matrix Multiplication and Trust Computations

ﬁrst player cooperates with two well placed players

she can recover the private value of a player in be-

tween. In the trust evaluation setting every malicious

player plays the role of the ﬁrst player in its row and

therefore as soon as there is a collaboration, there is a

risk of leakage. To mitigate this cooperation risk, our

idea is to repeat the dot product protocol in random or-

ders, except for the ﬁrst player. To access a given pri-

vate value, the malicious adversaries have to be well

placed in every occurrence of the protocol. Therefore

if their placement is chosen uniformly at random the

probability that they recover some private value di-

minishes with the number of occurrences. In practice,

they use a pseudo, but unpredictable, random gener-

ator to decide their placement: as each of them has

to know their placement, they can for instance use a

cryptographic hash function seeded with the alphabet-

ical list of the players distinguished names, with the

date of the day and with random values published by

each of the players. We detail the overall procedure

only for one dot-product, within the PDSMM

proto-

col. Each player except the ﬁrst one masks his coef-

ﬁcient v as in a simple wiretap channel (Ozarow and

Wyner, 1984), as sketched in Algorithm 4.

Algorithm 4: Wiretap repetition of the dot-product.

1: The players agree on d occurrences.

2: Each player computes his placement order in

each occurrence of the protocol from the cryp-

tographic hash function.

3a: With a shared modulus cryptosystem, the players

should share a common modulo M satisfying Hy-

pothesis (4). In the ﬁrst occurrence, each player

then masks his private input coefﬁcient v

with

d − 1 random values λ

j,i

∈ Z/MZ: v

−

∑

i=2

j,i

3b: With a Paillier-like cryptosystem, the players

choose their moduli according to Hypothesis (5),

where B

is replaced by dB

, in groups of size

n = 4 (the requirements of (5) on the moduli are

somewhat sequential, but can be satisﬁed inde-

pendently if each modulo is chosen in a distinct

interval larger than 3dB

). Then, in the ﬁrst oc-

currence, each player P

masks his private input

coefﬁcient v

with d −1 random values 0 ≤ λ

j,i

B: v

∑

i=2

(B − λ

j,i

) < dB.

4: Then for each subsequent occurrence, each player

replaces its coefﬁcient by one of the λ

j,i

5: In the end, the ﬁrst player has gathered d dot-

products and just needs to sum them in order to

recover the correct one.

Theorem 3. Algorithm 4 correctly allows the ﬁrst

player to compute the dot-product.

Proof. First, in a shared modulus setting, af-

ter the ﬁrst occurrence, Alice (P

) gets S

∑

j=2



−

∑

i=2

j,i



. Then in the following oc-

currences, Alice gets S

∑

j=2

j,i

. Finally she

computes

∑

i=1

∑

j=2

. Second, similarly,

in a Paillier-like setting, after the ﬁrst occurrence,

Alice recovers S

∑

j=2



∑

i=2

(B − λ

j,i

)



Then in the following occurrences, Alice gets

∑

j=2

j,i

. Finally she computes

∑

i=1

−

(d − 1)B(

∑

j=2

) =

∑

j=2

+ (d − 1)B) − (d −

1)Bu

∑

j=2

We give now the probability of avoiding attacks in

the case when n = 2t + 1, but the probability in the

even case should be close.

Theorem 4. Consider n = 2t + 1 players, grouped

by 3, of which k ≤ n − 2 are malicious and co-

operating, including the ﬁrst one Alice. Then, it

is on average sufﬁcient to run Algorithm 4 with

d ≤ 2ln



min{k − 1,n − k,

n−1

}



1 +

k−1

n−k−1



occur-

rences, to prevent the malicious players from recov-

ering any private input of the non malicious ones.

Proof. The idea is that for a given private input of

a non malicious player Bob, to be revealed to Alice,

Bob needs to be placed between cooperating mali-

cious adversaries at each occurrence of the protocol.

If there is only one non malicious player, then noth-

ing can be done to protect him. If there is 2 non ma-

licious, they are safe if they are together one time,

this happens with probability

n−2

, and thus on av-

erage after n − 2 occurrences. Otherwise, PDSMM

uses t =

n−1

groups of 3, including Alice. Thus,

each time a group is formed with one malicious and

one non malicious other players, Alice can learn the

private value of the non malicious player. Now, af-

ter any occurrence, the number a of attacked play-

ers is less than the number of malicious players mi-

nus 1 (for Alice) and obviously less than the num-

ber of non malicious players: 0 ≤ a < min{k −

1,n − k}. Thus let b = k − 1 − a and c = n − k − a.

In the next occurrence, the probability of saving at

least one more non malicious is

a(a−1+c)(n−3)!

(n−1)!

n−1

a(a−1+c)

2(n−2)

a(n−k−1)

2(n−2)

, so that the average num-

ber of occurrences to realize this is E

n,k

(a) =

2(n−2)

a(n−k−1)

. Thus, T

n,k

(a), the average number of oc-

currences to save all the non malicious players, sat-

isﬁes T

n,k

(a) ≤ E

n,k

(a) + T

n,k

(a − 1) ≤

∑

i=a

n,k

(i) +

n,k

(2) = (

∑

i=a

)

2(n−2)

n−k−1

+ T

n,k

(2). With 2 attacked

and c saved, T

n,k=n−c−2

(2) =

n−2

c+1

so that T

n,k

(a) ≤

−

)

2(n−2)

n−k−1

n−2

n−k−1

, where bounds on the Har-

monic numbers give H

≤ ln a (see, e.g., (Batir,

SECRYPT 2016 - International Conference on Security and Cryptography

2011)) and since a ≤ k − 1 and a ≤ n − k, this

shows also that 2a ≤ n − 1. Therefore, T

n,k

(a) ≤

2ln



min{k − 1,n − k,

n−1

}



n−2

n−k−1

For instance, if k, the number of malicious insid-

ers, is less than the number of non malicious ones,

the number of repetitions sufﬁcient to prevent any at-

tack is on average bounded by O (log k). To guaranty

a probability of failure less than ε, one needs to con-

sider also the worst case. There, we can have k = n−2

malicious adversaries and the number of repetitions

can grow to nln(1/ε):

Proposition 1. With n = 2t + 1, the number d of ran-

dom ring repetitions of Algorithm 4 to make the prob-

ability of breaking the protocol lower than ε satisﬁes

d < n ln(1/ε) in the worst case.

Proof. There are at least 2 non-malicious players,

otherwise the dot-product reveals the secrets in any

case. Any given non-malicious player is safe from

any attacks if in at least one repetition he was paired

with another non-malicious player. In the worst

case, k = n − 2 players are malicious and the latter

event arises with probability (1 −

n−1

)

for d repeti-

tions. If d ≥ n



−1



, then d > (n − 1)(−lnε) >

lnε

(

1−

n−1

)

, which shows that (1 −

n−1

)

< ε.

Overall, the wiretap variant of Algorithm 4 can

guaranty any security, at the cost of repeating the pro-

tocol. As the number of repetitions is ﬁxed at the be-

ginning by all the players, all these repetitions can oc-

cur in parallel. Therefore, the overall volume of com-

munication is multiplied by the number of repetitions,

while the number of rounds remains constant. This is

summarized in Table 1 and Figure 4, for the average

(Theorem 4) and worst (Proposition 1) cases of Al-

gorithm 4, and where the protocols of the previous

sections are also compared.

Table 1: Communication complexities.

Protocol Volume Rounds Paillier

MPWP O





O (n) 7

P-MPWP (§ 4) n

2+o(1)

O (n) 3

Alg. 4 (Wiretap) n

2+o(1)





5 3

Alg. 1 (DSDP

) n

1+o(1)

O (n) 3

Alg. 3 (PDSMM

) n

1+o(1)

5 3

Alg. 4 (Average) n

1+o(1)

5 3

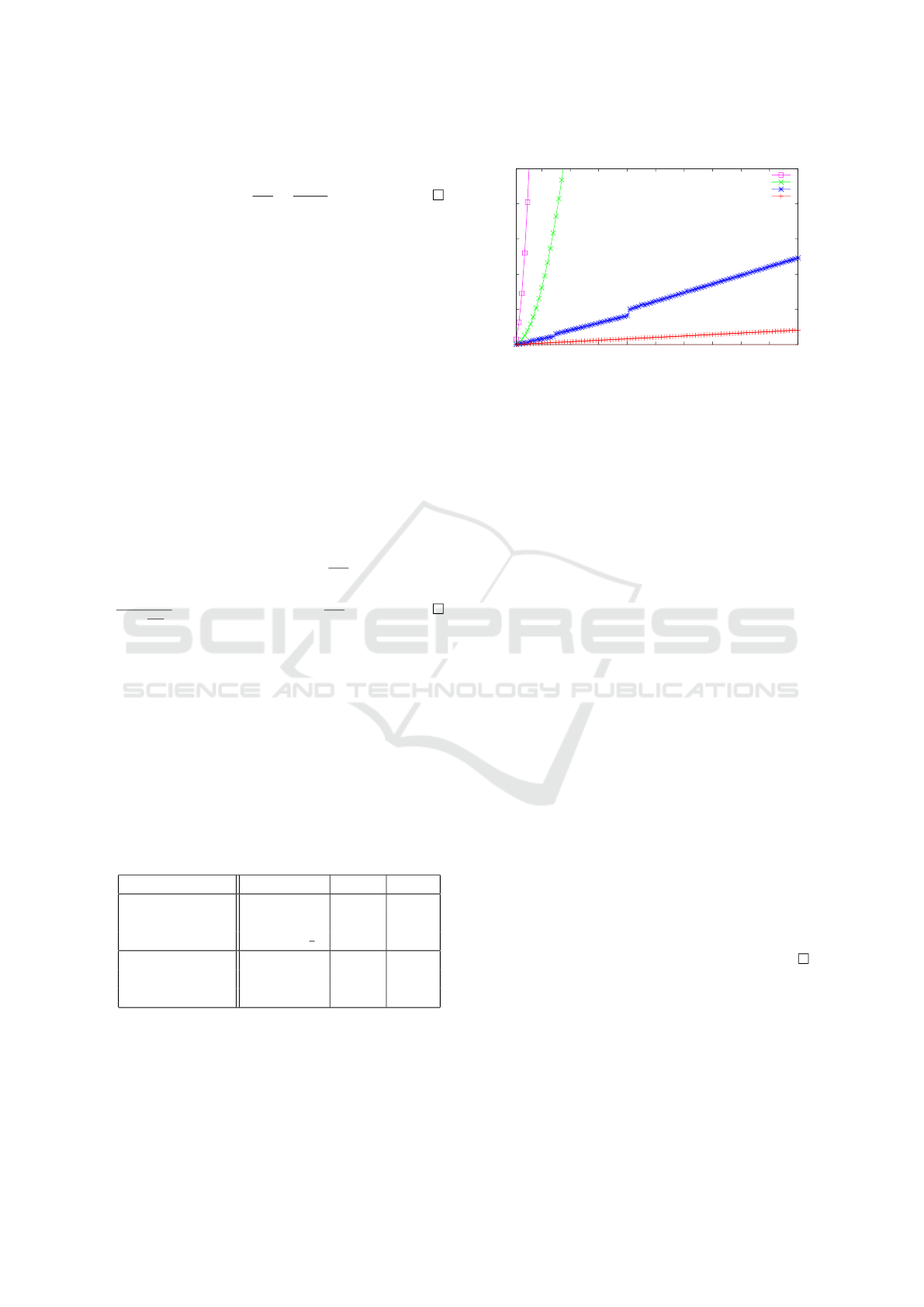
On the one hand, we see in Figure 4 that quadratic

protocols, with homomorphic encryption, are not us-

able for a realistic large group of players (trust aggre-

gation could be used for instance by certiﬁcate author-

ities, and there are several hundreds of those in current

operating systems or web browsers). On the other

200

400

600

800

1000

100 200 300 400 500 600 700 800 900 1000

time (s)

players

dot-product protocols with 2048 bits Paillier on a single core of an i5-4690 3.50GHz

Random Ring Wiretap (worst-case)

P-MPWP

Random Ring Wiretap (average: log(n))

DSDP

Figure 4: Quadratic and linear protocols timings.

hand, quasi linear time protocols present good per-

formance, while preserving some reasonable security

properties: the average wiretap curve is on average

sufﬁcient to prevent any attack and still has a quasi

linear asymptotic behavior. The steps in this curve

are the rounding of log(n) to the next integer and cor-

respond to one more random ring wiretap round.

8 CONCLUSION: MPC OF TRUST

We now come back to the aggregation of trust. As

shown in Section 3, the ﬁrst step is to reduce the com-

putation to that of dot-products. We show how to fully

adapt the protocol of Section 5 to the evaluation of

trust values with parallel and sequential aggregations:

Corollary 1. The protocol DSDP of Algorithm 1 can

be applied on trust values, provided that the random

values r

are invertible for z.

Proof. • u

, v

, r

, c

, α

, β

, ∆

, γ are now couples;

• Encryption and decryption (E(v

), D(β

), E(∆

E(γ), etc.) now apply on couples, using the mor-

phism E(ha,bi) = hE(a),E(b)i;

• α

is E((u

)zr

) = Add(Mul(E(v

);u

);r

and can still be computed by P

, since c

= E(v

)

and u

and r

are known to him;

• Similarly, β

= E(α

z∆

) = Add(E(α

);∆

• Finally, as z is commutative, S is recovered by

adding the inverses for z of the r

From (Dumas and Hossayni, 2012, Deﬁnition 11),

the d-aggregation of trust is a dot-product but slightly

modiﬁed to not include the value u

. Therefore at

line 3, in the protocol of Algorithm 3, it sufﬁces to

set s to the neutral element of z (that is s ← h0, 1i,

instead of s ← a

i, j

There remains to encode trust values that are pro-

portions, in [0, 1], into D = Z/NZ. With n par-

Private Multi-party Matrix Multiplication and Trust Computations

ticipants, we use a ﬁxed precision 2

−p

such that

n(2p+1)

< N ≤ 2

n(2(p+1)+1)

and round the trust co-

efﬁcients to bx2

c mod N from [0,1] → D. Then the

dot-product can be bounded as follows:

Lemma 7. If each coefﬁcient of the u

and v

are

between 0 and 2

− 1, then the coefﬁcients of S =

i=1

) are bounded by 2

n(2p+1)

in absolute

value.

Proof. For all u, v, the coefﬁcients of (uFv) are be-

tween 0 and (2

− 1)(2

− 1) + (2

− 1)(2

− 1) =

2p+1

− 2

p+2

+ 2 < 2

2p+1

− 1 for p a positive integer.

Then, by induction, when aggregating k of those with

z, the absolute values of the coefﬁcients remain less

than 2

k(2p+1)

− 1.

Therefore, with N an 2048 bits modulus and n ≤

4 in the ESDP protocols of Algorithm 3, Lemma 7

allows a precision close to 2

−255

≈ 10

−77

In conclusion, we provide an efﬁcient and secure

protocol DSDP

to securely compute dot products

(against semi-honest adversary) in the MPC model,

with unsual data division between n players. It can be

used to perform a private matrix multiplication and

also be adapted to securely compute trust aggregation

between players.

REFERENCES

Amirbekyan, A. and Estivill-Castro, V. (2007). A new ef-

ﬁcient privacy-preserving scalar product protocol. In

AusDM 2007, volume 70 of CRPIT, pages 209–214.

Batir, N. (2011). Sharp bounds for the psi function and har-

monic numbers. Mathematical inequalities and appli-

cations, 14(4).

Ben-Or, M., Goldwasser, S., and Wigderson, A. (1988).

Completeness theorems for non-cryptographic fault-

tolerant distributed computation. In STOC’88. ACM.

Benaloh, J. (1994). Dense probabilistic encryption. In

SAC’94.

Bendlin, R., Damg

ard, I., Orlandi, C., and Zakarias, S.

(2011). Semi-homomorphic encryption and multi-

party computation. In EUROCRYPT’11, LNCS.

Blanchet, B. (2001). An efﬁcient cryptographic protocol

veriﬁer based on prolog rules. In IEEE CSFW’01.

Blanchet, B. (2004). Cryptographic Protocol Veriﬁer User

Manual.

Chaum, D., Evertse, J., van de Graaf, J., and Peralta, R.

(1986). Demonstrating possession of a discrete loga-

rithm without revealing it. In CRYPTO’86.

Damg

ard, I., Pastro, V., Smart, N., and Zakarias, S. (2012).

Multiparty computation from somewhat homomor-

phic encryption. In CRYPTO’12, LNCS. Springer.

Delaune, S. (2006). An undecidability result for agh. Theor.

Comput. Sci.

Dolev, S., Gilboa, N., and Kopeetsky, M. (2010). Com-

puting multi-party trust privately: in O(n) time units

sending one (possibly large) message at a time. In

SAC’10. ACM.

Du, W. and Atallah, M. J. (2001). Privacy-preserving co-

operative statistical analysis. In ACSAC ’01, pages

102–110.

Du, W. and Zhan, Z. (2002). A practical approach to

solve secure multi-party computation problems. In

NSPW’02. ACM.

Dumas, J.-G. and Hossayni, H. (2012). Matrix powers al-

gorithm for trust evaluation in PKI architectures. In

STM’12, ESORICS 2012, LNCS.

Foley, S. N., Adams, W. M., and O’Sullivan, B. (2010). Ag-

gregating trust using triangular norms in the keynote

trust management system. In STM’2010.

Fousse, L., Lafourcade, P., and Alnuaimi, M. (2011). Be-

naloh’s dense probabilistic encryption revisited. In

AFRICACRYPT’11.

Goethals, B., Laur, S., Lipmaa, H., and Mielik

ainen, T.

(2005). On private scalar product computation for

privacy-preserving data mining. In ICISC’04, LNCS.

Springer.

Guha, R. V., Kumar, R., Raghavan, P., and Tomkins,

A. (2004). Propagation of trust and distrust. In

WWW’2004.

Huang, J. and Nicol, D. M. (2010). A formal-semantics-

based calculus of trust. IEEE Internet Computing.

Jøsang, A. (2007). Probabilistic logic under uncertainty. In

CATS’2007.

Lafourcade, P. and Puys, M. (2015). Performance eval-

uations of cryptographic protocols veriﬁcation tools

dealing with algebraic properties. In FPS’15.

Lindell, Y. (2009). Secure computation for privacy pre-

serving data mining. In Encyclopedia of Data Ware-

housing and Mining, Second Edition 4 Volumes). IGI

Global.

Michalas, A., Dimitriou, T., Giannetsos, T., Komninos, N.,

and Prasad, N. R. (2012). Vulnerabilities of decen-

tralized additive reputation systems regarding the pri-

vacy of individual votes. Wireless Personal Commni-

cations, 66(3):559–575.

Mohassel, P. (2011). Efﬁcient and secure delegation of lin-

ear algebra. IACR Cryptology ePrint Archive.

Ozarow, L. H. and Wyner, A. D. (1984). Wire-tap channel

II. In EUROCRYPT’84.

Paillier, P. (1999). Public-key cryptosystems based on com-

posite degree residuosity classes. In EUROCRYPT’99.

Shamir, A. (1979). How to share a secret. CACM, 22(11).

Wang, I.-C., Shen, C.-H., Hsu, T.-S., Liao, C.-C., Wang, D.-

W., and Zhan, J. (2008). Towards empirical aspects of

secure scalar product. In ISA’08.

Yao, A. C. (1982). Protocols for secure computations.

2013 IEEE 54th Annual Symposium on Foundations

of Computer Science.

SECRYPT 2016 - International Conference on Security and Cryptography