
Analytical Models for Evaluating Effectiveness of
Compressed File Transfers in Mobile Computing
Armen Dzhagaryan and Aleksandar Milenković
Electrical and Computer Engineering Department, The University of Alabama in Huntsville,
301 Sparkman Drive, Huntsville, AL, U.S.A.
Keywords: Mobile Sensing, Networks, Lossless Compression, Energy Efficiency, Performance Evaluation.
Abstract: The importance of optimizing data transfers between mobile computing devices and the cloud is increasing
with an exponential growth of mobile data traffic. Lossless data compression can be essential in increasing
communication throughput, reducing communication latency, achieving energy-efficient communication,
and making effective use of available storage. In this paper we introduce analytical models for estimating
effective throughput and energy efficiency of uncompressed data transfers and compressed data transfers
that utilize common compression utilities. The proposed analytical models are experimentally verified using
state-of-the-art mobile devices. These models are instrumental in developing a framework for seamless
optimization of data file transfers.
1 INTRODUCTION
Mobile computing devices such as smartphones,
tablets, and e-readers, have become the dominant
platforms for consuming digital information. On the
other side, Internet-of-Things (IoT) devices have
become an important source of digital information.
Data traffic initiated from mobile computing devices
and Internet-of-Things devices has been growing
exponentially over the last several years. A Cisco
report states that the global mobile data traffic grew
69% in 2014 relative to 2013, reaching 2.5 exabytes
per month (CISCO, 2015). This is an over 30-fold
increase relative to the total Internet traffic in 2000.
It is forecast that the global mobile data traffic will
grow nearly 10-fold from 2014 to 2019, reaching
24.3 exabytes per month.
Lossless data compression can increase
communication throughput, reduce latency, save
energy, and increase available storage. However,
compression introduces additional overhead that
may exceed any gains due to transferring or storing
fewer bytes. Compression utilities on mobile
computing platforms differ in compression ratio,
compression and decompression speeds, and energy
requirements. When transferring data, we would like
to have an agent to determine whether compressed
transfers are beneficial, and, if so, select the most
beneficial compression utility. A first step toward
designing such an agent is to obtain a good
understanding of various parameters impacting the
efficiency of data transfers.
Lossless data compression is currently being
used to reduce the required bandwidth during file
downloads and to speed up web page loads in
browsers. Google’s Flywheel proxy (Agababov et
al., 2015), Google Chrome (Google, 2014a),
Amazon Silk (Amazon, 2015), as well as the mobile
applications Onavo Extend (Onavo, 2015) and
Snappli (Snappli, 2014) use proxy servers to provide
HTTP compression for all pages during web
browsing. For file downloads, several Google
services, such as Gmail and Drive, provide zip
compression (zlib, 2015) of attachments and files
(Google, 2014b). Similarly, application stores such
as Google Play and Apple’s App Store use zip or
zip-derived containers for application distribution.
Several Linux distributions are also using common
compression utilities such as gzip, bzip2, and xz for
their software repositories.
The importance of lossless compression in
network data transfers has also been recognized in
academia (Barr and Asanović, 2003; 2006;
Dzhagaryan et al., 2013). Recent studies
(Dzhagaryan et al., 2015; Milenkovic et al., 2013b)
focused on a measurement-based experimental
evaluation of compressed and uncompressed file
transfers on the state-of-the-art mobile devices.
40
Dzhagaryan, A. and Milenkovi
´
c, A.
Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing.
DOI: 10.5220/0005953700400051
In Proceedings of the 6th International Joint Conference on Pervasive and Embedded Computing and Communication Systems (PECCS 2016), pages 40-51
ISBN: 978-989-758-195-3
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

These studies showed that selected compressed
transfers over a WLAN and cellular interfaces
outperform corresponding uncompressed file
transfers. However, not a single combination of a
compression utility and a compression level
performs the best for all file transfers and network
conditions. A number of parameters may impact the
effectiveness of file uploads and downloads initiated
on a mobile device. These parameters include the
type of network interface (e.g., cellular, WLAN),
network connection throughput and latency, type
and size of transferred files, mobile device
performance, and energy characteristics.
In this paper, we propose analytical models for
estimating the effectiveness of uncompressed data
transfers and compressed data transfers that use
common compression utilities and their compression
levels. As a measure of effectiveness, we use the
effective upload and download throughputs
expressed in megabytes per second. In addition, we
consider energy efficiency expressed in megabytes
per Joule. The analytical models describe effective
upload and download throughputs and energy
efficiencies for uncompressed and compressed data
transfers as a function of parameters such as:
Uncompressed (raw) file size;
Local compression and decompression
throughput or energy efficiency;
Compression ratio;
Network parameters including network
connection throughput or energy efficiency, time
or energy to setup a network connection.
We experimentally verify the proposed models on
Google’s Nexus 4 and OnePlus One smartphones.
The proposed models are instrumental in developing
a framework for optimized data transfer between
mobile computing devices and the cloud. The
framework relies on agents running on mobile
devices and the cloud to select effective modalities
for file uploads and downloads.
The rest of this paper is organized as follows.
Section 2 presents background for our study. It gives
a system view of file transfers (2.1) and makes a
case for optimizing file transfers (2.2). Section 3
describes the design and verification of analytical
models for uncompressed file transfers. Section 4
describes the design and verification of analytical
models for compressed file transfers. Finally,
Section 5 summarizes our findings and draws
conclusions.
2 BACKGROUND
2.1 File Transfers in Mobile Cloud
Figure 1 illustrates file uploads and downloads that
are initiated from a mobile device. A data file can be
uploaded uncompressed or compressed. In a case of
uncompressed uploads, an uncompressed file (UF) is
uploaded over a network interface. In a case of
compressed uploads, the uncompressed file is first
compressed locally on the device, and then a
compressed file (CF) is uploaded over the network.
Similarly, a file can be downloaded from the cloud
uncompressed or compressed. In a case of
compressed downloads, a compressed version of the
requested file is downloaded from the cloud, and
then the compressed file is decompressed locally on
the mobile device. Compressed uploads and
downloads utilize one of the available compression
utilities. Each compression utility typically supports
a range of compression levels that allow us to trade
off speed for compression ratio. Lower levels favor
speed, whereas higher levels result in better
compression.
Figure 1: Uncompressed and compressed data flows
between mobile devices and the cloud.
In this paper for compressed transfers, we
consider six common compression utilities described
in Table. We have selected relatively fast gzip and
lzop utilities, as well as bzip2 and xz, which provide
a high compression ratio. We also consider pigz and
pbzip2, parallel version of gzip and bzip2,
respectively, because modern mobile devices
routinely include multicore processors. For each
utility, we consider at least three compression levels:
low (L), medium (M), high (H), as described in
Table 1.
To evaluate the effectiveness of a networked file
transfer we need to determine the total time to
complete the transfer. This time, in general, includes
the following components: (i) sender overhead time,
(ii) network connection setup time, (iii) file
Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing
41

transmission time, and (iv) receiver overhead time.
To measure the effectiveness of data transfers we
use the effective throughput rather than the total
transfer time. The effective upload or download
throughput, measured in megabytes per second, is
defined as the ratio between the uncompressed file
size in megabytes and the time needed to complete
the file transfer. This metric thus captures the
system’s ability to perform a file transfer in the
shortest period of time regardless of a transfer mode.
Table 1: Compression Utilities.
Utility
Levels (Default)
[L, M, H]
Version Notes
gzip 1-9 (6) [1,6,9] 1.6
DEFLATE (Ziv-
Lempel, Huffman)
lzop 1-9 (6) [1,6,9] 1.03
LZO (Lempel-Ziv-
Oberhumer)
bzip2 1-9 (6) [1,6,9] 1.0.6
RLE+BWT+MTF+RL
E+Huffman
xz 1-9 (6) [1,6,9] 5.1.0a LZMA2
pigz 1-9 (6) [1,6,9] 2.3 Parallel gzip
pbzip2 1-9 (9) [1,6,9] 1.1.6 Parallel bzip2
Another metric of interest for networked file
transfers initiated on mobile devices is energy
efficiency. The energy consumed for compression
and decompression can be a decisive factor in
battery-powered mobile devices. Achieving a higher
compression ratio requires more computation and,
therefore, more energy, but better compression
reduces the number of bytes, thus saving energy
when transmitting the data. The energy efficiency,
measured in megabytes per Joule, is defined as the
ratio between the uncompressed file size in
megabytes and the total energy needed to complete
the file transfer. This metric thus captures the
system’s ability to perform a file transfer while
consuming the least energy.
The effective upload and download throughputs
and energy efficiencies depend on many factors,
including the file size and type, selected
compression utility, the compression level, network
characteristics such as latency and throughput, as
well as the smartphone’s performance and energy-
efficiency. Whereas previous studies showed that
compressed uploads and downloads can save time
and energy in many typical file transfers initiated
from smartphones (Dzhagaryan et al., 2015;
Dzhagaryan and Milenkovic, 2015; Milenkovic et
al., 2013b) there is not a single upload or download
file transfer method that works the best for all data
types and network conditions. To underscore this
problem, we conduct a measurement-based study
that evaluates the effectiveness of various data
transfer options under different network conditions.
For the evaluation, we use Google’s Nexus 4
(Google, 2014c, p. 4) and OnePlus One (OnePlus,
2015) smartphones and the measurement setup
described in (Dzhagaryan et al., 2016, 2015).
2.2 Why Optimize File Transfers?
In this section, we show the results of a
measurement-based study that evaluates the
effectiveness of uncompressed and compressed file
transfers initiated on a mobile device. We show that
a compression utility, compression level pair that
achieves the maximum throughput or energy
efficiency changes as a function of network
conditions and file size and type.
Upload Example. We consider uploading a text file
that contains a summary of user’s physiological state
captured every second by a wearable Zephyr
Technologies BioHarness 3 chest belt. The file
contains information about user’s heart rate,
breathing rate, activity level, and body posture. The
file is periodically uploaded to the cloud for future
analysis and long-term storage, e.g. in health
monitoring applications. The file size is 4.69 MB.
The experiment involves uncompressed and
compressed file uploads from an OnePlus One
smartphone to a remote server over the Internet. For
each type of a transfer, the time to upload the file
and energy consumed are measured to determine the
upload throughput and energy efficiency. To
demonstrate the impact of network connection
parameters, the measurements are performed when
the WLAN network throughput is set to 0.5 MB/s
(low) and 5 MB/s (high).
Table shows the effective upload throughputs
and the energy efficiencies for all types of file
uploads. The two bottom rows show speedups in the
effective throughput and energy efficiency when
comparing the best performing compressed upload
to the uncompressed upload [best/raw] and to the
compressed upload using gzip -6 [best/gzip-6],
which is considered a default compression mode.
The uncompressed upload on a 0.5 MB/s
network achieves the effective throughput of
0.51 MB/s and the effective energy efficiency of
0.88 MB/J. The compressed upload with gzip -6
achieves the effective throughput and energy
efficiency of 4.05 MB/s and 3.82 MB/J,
respectively. The best effective throughput of
4.83 MB/s is achieved with xz -0, while the best
energy efficiency of 4.55 MB/J is achieved with
gzip -1. Selecting the best compression mode
(utility, level) for throughput achieves 9.43- and
1.19-fold improvements over the uncompressed and
PEC 2016 - International Conference on Pervasive and Embedded Computing
42
the default compressed upload, respectively.
Selecting the best compression mode for energy
efficiency achieves 5.15 and 1.19-fold
improvements over the uncompressed and the
default compressed upload.
Table 2: Throughput and energy-efficiency for different
uploading modes of Summary.csv over WLAN.
Utility & Level CR
Effective
Throughput
[MB/s]
Energy
Efficiency
[MB/J]
Net Thr. [MB/s] - 0.5 5.0 0.5 5.0
gzip 1 7.05 2.97 9.25 4.55 11.24
gzip 6 10.60 4.05 6.07 3.82 5.42
gzip 9 11.69 2.15 2.24 1.39 1.40
lzop 1 5.14 2.20 7.98 3.58 11.68
lzop 6 5.14 2.25 8.46 3.95 10.60
bzip2 1 16.91 2.55 2.59 1.53 1.47
bzip2 6 17.48 1.79 1.83 1.07 1.08
bzip2 9 17.43 1.68 1.71 0.96 0.98
xz 0 13.66 4.83 7.66 4.45 6.29
xz 6 16.86 0.49 0.49 0.28 0.28
xz 9 16.86 0.48 0.49 0.28 0.27
pigz 1 7.06 2.92 8.05 4.34 8.42
pigz 6 10.61 4.12 10.73 4.27 6.73
pigz 9 11.69 4.19 6.59 1.66 1.92
raw - 1.00 0.51 3.16 0.88 2.99
[best/raw] - - 9.43 3.40 5.15 3.90
[best/gzip-6] - - 1.19 1.77 1.19 2.15
The uncompressed upload on a 5 MB/s network
achieves the effective throughput of 3.16 MB/s and
the effective energy efficiency of 2.99 MB/J. The
compressed upload with gzip -6 achieves the
effective throughput and energy efficiency of
6.07 MB/s and 5.42 MB/J, respectively. Selecting
the best compression mode for throughput achieves
3.4 and 1.77-fold improvements over the
uncompressed and the default compressed upload,
respectively. Selecting the best compression mode
for energy efficiency achieves 3.9 and 2.15-fold
improvements over the uncompressed and the
default compressed upload, respectively.
Download Example. In this example, we consider
downloading an Android executable file for the
Telegram application (telegram.tar). To prepare the
input file, the original apk file is extracted into an
uncompressed tar file. The file size is 22.34 MB.
The experiment involves uncompressed and
compressed file downloads initiated from the
OnePlus One smartphone. The server keeps the
uncompressed and compressed files available, so the
sender overhead is minimal. The total download
time includes the time needed to download and
decompress the requested file. The measurements
are performed when the WLAN network throughput
is set to 0.5 MB/s and 5 MB/s.
Table shows the effective download throughputs
and energy efficiencies. The two bottom rows show
speedups in the effective throughput and energy
efficiency when comparing the best performing
compressed download with the uncompressed and
with the compressed download using gzip -6.
Table 3: Throughput and energy-efficiency for different
downloading modes of Telegram.tar over WLAN.
Utility & Level CR
Throughput
[MB/s]
Energy
Efficiency
[MB/J]
WLAN Thr.[MB/s] - 0.5 5.0 0.5 5.0
gzip 1 1.87 0.90 7.91 1.65 7.61
gzip 6 1.95 0.98 8.28 1.74 7.58
gzip 9 1.95 0.96 8.11 1.80 7.76
lzop 1 1.56 0.73 6.89 1.38 8.31
lzop 6 1.56 0.77 6.93 1.46 8.03
bzip2 1 1.93 0.94 5.64 1.45 2.90
bzip2 6 1.93 0.97 4.98 1.37 2.52
bzip2 9 1.91 0.92 5.31 1.32 2.48
xz 0 2.13 1.07 8.16 1.76 4.77
xz 6 2.32 1.15 9.35 1.90 5.11
xz 9 2.32 1.10 9.56 1.82 5.06
pigz 1 1.93 0.92 8.12 1.69 9.04
pigz 6 1.93 0.92 8.29 1.72 9.34
pigz 9 1.91 0.98 7.30 1.87 8.36
raw - 1.00 0.48 4.55 0.92 5.35
[best/raw] - 2.41 2.10 2.07 1.75
[best/gzip-6] - 1.17 1.15 1.09 1.23
The uncompressed download on a 0.5 MB/s
network achieves the effective throughput of
0.48 MB/s and the energy efficiency of 0.92 MB/J.
The compressed download with gzip -6 achieves the
effective throughput of 0.98 MB/s and the energy
efficiency of 1.74 MB/J. The best effective
download throughput of 1.15 MB/s and the best
energy efficiency of 1.90 MB/J are achieved with xz
-6. Thus, xz -6 achieves 2.41 and 1.17 times better
throughput than the uncompressed download and the
compressed download with gzip -6, respectively.
Similarly, it achieves 2.07 and 1.09 times better
energy efficiency than the uncompressed and the
default compressed download, respectively.
The uncompressed download on a 5 MB/s
network achieves the effective throughput of
4.55 MB/s and the effective energy efficiency of
5.35 MB/J. The default compressed download
achieves the effective throughput and the energy
efficiency of 8.28 MB/s and 7.58 MB/J,
respectively. Selecting the best decompression mode
for throughput, xz -9, achieves 2.1 and 1.15-fold
improvement over the uncompressed and the default
compressed download, respectively. Selecting the
best decompression mode for energy efficiency, pigz
-6, achieves 1.75- and 1.23-fold improvements over
Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing
43

the uncompressed and the default compressed
download, respectively.
These examples demonstrate that not a single
combination of a compression utility and level offers
the best throughputs and energy efficiencies in all
conditions. The file size, file type, device
performance, energy characteristics, and network
conditions, all impact the choice of the best
performing file upload or download combination.
However, these examples also show that the best
performing compression mode provides a substantial
increase in the effective throughput and energy
efficiency when compared to the uncompressed or
the default compressed data transfers.
Ideally, we would like to design a framework for
near optimal file transfers between mobile devices
and the cloud. The framework would autonomously
in real-time and with minimal overhead make a
selection of a near optimal file transfer mode while
taking into account all parameters discussed above.
In this paper, we describe analytical models for
uncompressed and compressed file transfers which
will serve as first steps in implementing the
framework for near optimal data transfers.
3 UNCOMPRESSED TRANSFERS
3.1 Modeling Uncompressed Transfers
The total time to perform a file transfer includes
sender overhead time, network connection setup
time, file transmission time, and receiver overhead
time. In a case of uncompressed file uploads, the
sender and receiver overheads can be ignored. Thus,
the total time of an uncompressed file upload,
T.UUP, includes the time to setup a network
connection, T.SC, and the file transmission time,
T.UP, as shown in Equation (1). If we know the
network upload throughput, Th.UP, the file
transmission time for upload can be calculated as the
ratio between the file size and the network upload
throughput, T.UP=US/Th.UP. Similarly, the total
time of an uncompressed file download, T.UDW,
includes T.SC and the file transmission time, T.DW,
as shown in Equation (2). The file transmission time
for download can be calculated as
Th.DW=US/Th.DW, where Th.DW is the network
download throughput.
The effective upload throughput is calculated as
the uncompressed file size in megabytes, US,
divided by the total time to upload the file,
Th.UUP=US/T.UUP. The effective download
throughput, Th.UDW, is calculated as the
uncompressed file size, US, divided by the total time
to download the file, Th.UDW=US/T.UDW.
Equations (3) and (4) show the expressions for the
effective upload and download throughputs,
respectively. The effective throughputs depend on
the file size, the time to set up the network
connection, and the network upload and download
throughputs. The effective throughputs, Th.UUP
[Th.UDW], reach the network throughputs, Th.UP
[Th.DW], when transferring very large files. In a
case of smaller files, the time to setup the network
connection limits the effective throughput.
...
(1)
...
(2)
.
.
1.∙./
(3)
.
.
1.∙./
(4)
...
(5)
...
(6)
.
.
1.∙./
(7)
.
.
1.∙./
(8)
The energy consumed by an uncompressed file
upload, ET.UUP, includes the energy spent while
setting up the network connection, ET.SC, and the
energy needed to upload the file, ET.UP, as shown
in Equation (5). If we know the energy-efficiency of
the network connection for uploads, EE.UP, we can
calculate ET.UP as ET.UP=US/EE.UP. Similarly,
the energy consumed by an uncompressed file
download, ET.UDW, includes the energy needed to
establish the connection and the energy needed to
download the file, ET.DW, as shown in Equation (6).
The effective upload energy efficiency, EE.UUP, is
calculated as the uncompressed file size in
megabytes, US, divided by the total energy needed
to upload the file, EE.UUP=US/ET.UUP. The
effective download energy efficiency, EE.UDW, is
calculated as the uncompressed file size, US, divided
by the total energy needed to download the file,
EE.UDW=US/ET.UDW. Equations (7) and (8) show
the expressions for the upload and download energy
efficiencies, respectively. They imply that the
effective energy efficiencies, EE.UUP [EE.UDW],
reach the network energy efficiencies, EE.UP
[EE.DW], when transferring very large files.
PEC 2016 - International Conference on Pervasive and Embedded Computing
44
3.2 Model Verification
To verify the models described by the equations
from above, we perform a set of measurement-based
experiments as follows. An OnePlus One
smartphone is used to initiate a series of file uploads
to a server and a series of file downloads from a
server. For each file transfer, the execution time and
the energy consumed are measured using a
measurement setup that involves a battery simulator
(Dzhagaryan et al., 2016, 2015). The smartphone is
connected to the Internet over its WLAN interface,
and file transfers take place over a secure shell (ssh),
an encrypted network protocol. The file sizes are set
to vary from 1 kB to 100 MB. The upload and
download experiments are repeated for four distinct
network throughputs set to Th.UP = Th.DW
= 0.5 MB/s, 2.0 MB/s, 3.5 MB/s, and 5.0 MB/s.
a.
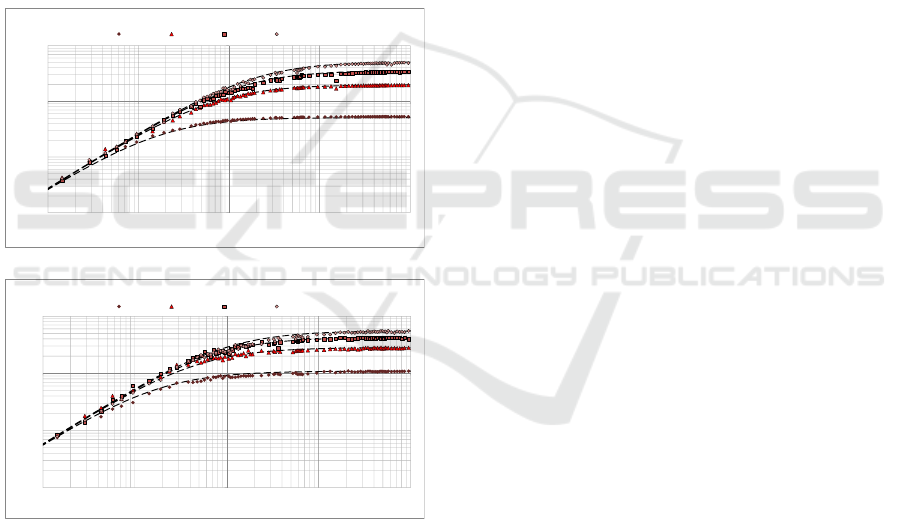
b.
Figure 2: Measured effective throughput and energy
efficiency for file uploads.
Figure 2(a) shows the measured effective
throughput for uncompressed uploads as a function
of the file size, US, and the network connection
throughput for uploads, Th.UP. The plots show that
the effective throughput saturates for the larger files,
reaching the network connection throughput, i.e.,
Th.UUP=Th.UP. By using a curve fitting, we derive
an equation that models the effective throughput.
The dashed lines in Figure 2(a) illustrate the derived
equation for different network upload throughputs.
The derived equation matches the Equation (3) from
the proposed analytical model. The constant that
corresponds to the time to setup the connection for
our setup, T.SC, is 0.39 seconds.
Figure 2(b) shows the measured effective energy
efficiency for the same set of experiments. By using
the curve fitting, we derive an equation that matches
the one described in Equation (4). The constant that
corresponds to the energy consumed while setting up
the communication channel for out setup, ET.SC, is
0.14 Joules.
We Perform a similar set of measurement-based
experiments for uncompressed file downloads for
different network throughputs. The experiment
results confirm the correctness of the proposed
analytical models for the effective throughput and
energy efficiency for uncompressed file downloads.
Derived constants for T.SC and ET.SC match the
ones derived from the upload experiments.
3.3 Profiling Network Connection
The experimental verification of the models for the
effective throughput and energy efficiency requires a
series of uploads and downloads of data files of
different sizes. However, such an approach is not
practical in real conditions because it takes
considerable time and requires instrumentation of
smartphone for performing energy measurements.
Here we describe a practical approach for deriving
unknown network parameters using the verified
analytical model and a limited number of
experiments. Specifically, we describe practical
experiments that derive the following parameters:
The network upload and download throughputs,
Th.UP [Th.DW], respectively;
The network upload and download energy
efficiencies, EE.UP [EE.DW], respectively;
The time and energy spent to setup the network
connection, T.SC [ET.SC].
The proposed method for deriving the network
parameters involves performing a two file upload or
download test. Two files of different sizes are
selected to be uploaded or downloaded over a
network connection with unknown parameters. The
time is measured during the transfers and used in
estimating energy consumption based on device
characteristics (using its idle current and the delta
current during file transfers). The calculated
throughputs or energy efficiencies are then used
within the models to derive the network parameters.
To demonstrate the derivation of network
parameters, we consider file uploads over an ssh
0.01
0.10
1.00
10.00
0.01 0.10 1.00 10.00 100.00
Th.UUP[MB/s]
US[MB]
Effectivethroughputforuploads
0.5MB/s 2.0MB/s 3.5MB/s 5.0MB/s
0.01
0.10
1.00
10.00
0.01 0.10 1.00 10.00 100.00
EE.UUP[MB/J]
US[MB]
Effectiveenergyefficiencyforuploads
0.5MB/s 2.0MB/s 3.5MB/s 5.0MB/s
Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing
45
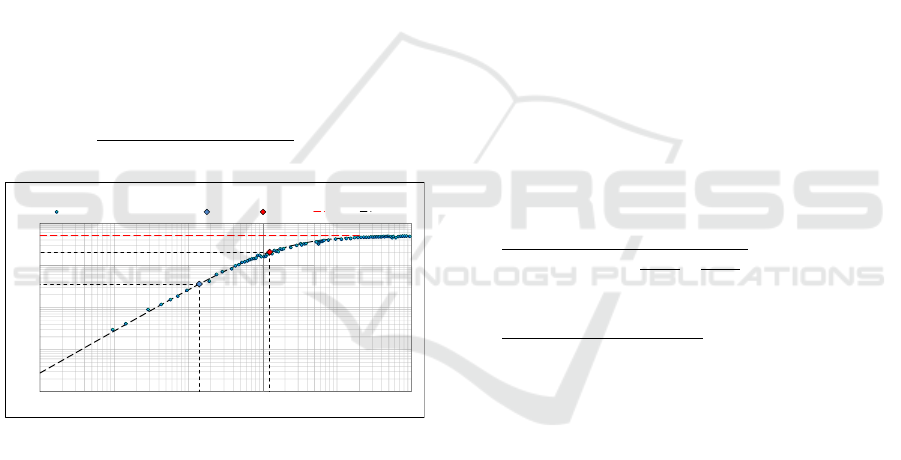
network connection that utilizes the smartphone’s
WLAN interface. The goal is to determine the T.SC
and Th.UP. We select two test files with sizes
US(s)=0.14 MB and US(l)=1.24 MB. The measured
effective throughputs are Th.UUP(s)=0.36 MB/s for
the 0.14 MB file and Th.UUP(l)=1.24 MB/s for the
1.24 MB file. Next, using Equation (9) for
calculating the effective network upload throughput,
we derive values of 5.167 MB/s and 0.362 seconds
for Th.UP and T.SC, respectively.
Figure 3 illustrates the proposed method for
characterizing network connection. The measured
upload throughputs for two selected files are marked
with a blue and a red diamond. By deriving Th.UP
and T.SC as described above, the model from
Equation (3) is plotted using a black dashed-dot
curve. The actual measurements of the effective
upload throughputs performed during the
verification phase are shown as blue circles. A visual
inspection shows that the model with parameters
extracted by just two measurements matches the
actual measurements performed during the
verification phase.
.
.
1.∙.
/
(9)
Figure 3: Extracting network parameters for uploads.
4 COMPRESSED TRANSFERS
A compressed upload of a data file to the cloud and
a compressed download from the cloud can be
performed in two ways, sequentially or with the use
of piping. In the former, for upload, the data file is
first compressed locally on the mobile device and
then compressed file is transferred to the cloud, with
no overlap between these two tasks. For download,
the compressed data file is downloaded on the
mobile device and then decompressed with no
overlap between these two tasks. In the later, for
upload and download, the file compression or
decompression times are partially or completely
hidden by the time to setup the network connection
and the file transmission time.
4.1 Performance Limits
The maximum compressed upload time shown in
Equation (10), T.CUP.max, includes the time to
perform the local compression of the file on the
mobile device, the time to setup network connection,
T.SC, and the time to transfer the compressed file,
T.CUP'. The time to transfer the compressed file can
be calculated as the compressed file size, which is
US/CR, where CR is the compression ratio, divided
by the network connection upload throughput
Th.UP. Instead of using the time to perform local
compression on a mobile device, T.C, we can use the
local compression throughput, Th.C, defined as the
uncompressed file size, US, divided by the time to
perform a local compression, T.C. This “higher is
better” metric captures ability of a mobile device to
perform local compression fast. The minimum
upload time shown in Equation (11), T.CUP.min,
includes the time to setup network connection, T.SC,
and the time to transfer the compressed file, T.CUP'.
.. ...′
(10)
.. ..′
(11)
..
∙.
1∙.∙
1
.
.
(12)
..
∙.
1∙.∙./
(13)
The minimum upload throughput, Th.CUP.min, is
calculated as the uncompressed file size in
megabytes, US, divided by the maximum time to
perform compressed upload, T.CUP.max. The
maximum upload throughput, Th.CUP.max, is
calculated as the uncompressed file size in
megabytes, US, divided by the minimum time to
perform compressed upload T.CUP.min. The final
expressions in Equations (12) and (13) show the
boundaries for the compressed upload throughputs
as a function of the network parameters, Th.UP and
T.SC, the file size, US, the compression ratio, CR,
and the local compression throughput, Th.C. From
these expressions, we can analytically estimate the
impact of changes in these parameters to the
effective throughputs. For example, the highest
compressed upload throughput that can be achieved
approaches the product of the compression ratio and
the network connection upload throughput, which is
possible in devices where local compression
0.00
0.01
0.10
1.00
10.00
0.00 0.01 0.10 1.00 10.00 100.00
Th.UUP[MB/s]
US[MB]
Extractingnetworkparametersforupload(througput)
Th.UUP(ActualMeasurements) 0.14MB 1.24MB Th.UP Th.UUP
PEC 2016 - International Conference on Pervasive and Embedded Computing
46
throughputs exceeds the network upload throughput
and when the size of a transferred file is sufficiently
large so that transfer time dwarfs the network
connection setup time.
The maximum total download time shown in
Equation (14), T.CDW.max, includes the time to
setup network connection, T.SC, the time to transfer
the compressed file, T.CDW', and the time to
perform the decompression of the received file on
the mobile device. The time to transfer the
compressed file can be calculated as the compressed
file size, US/CR, divided by the network connection
download throughput Th.DW. The time to perform
decompression on the mobile device, T.D, can be
used to determine the local decompression
throughput, Th.D, which is defined as the
uncompressed file size, US, divided by the time to
perform decompression. This metric thus captures
the mobile device’s ability to effectively perform
decompression. The minimum download time
shown in Equation (15), T.CDW.min, includes the
time to setup network connection, T.SC, and the time
to transfer the compressed file, T.CDW'.
.....′
(14)
....′
(15)
..
∙.
1∙.∙
1
.
.
(16)
..
∙.
1∙.∙./
(17)
The minimum effective compressed download
throughput, Th.CDW.min, is calculated as the
uncompressed file size in megabytes, US, divided by
the maximum time to perform compressed upload,
T.CDW.max. The maximum download throughput,
Th.CDW.max, is calculated as the uncompressed file
size in megabytes, US, divided by the minimum time
to perform the compressed download, T.CDW.min.
The final expressions in Equations (16) and (17)
show the boundaries for the compressed download
throughputs as a function of the network parameters,
file size, compression ratio, and the local
decompression throughput.
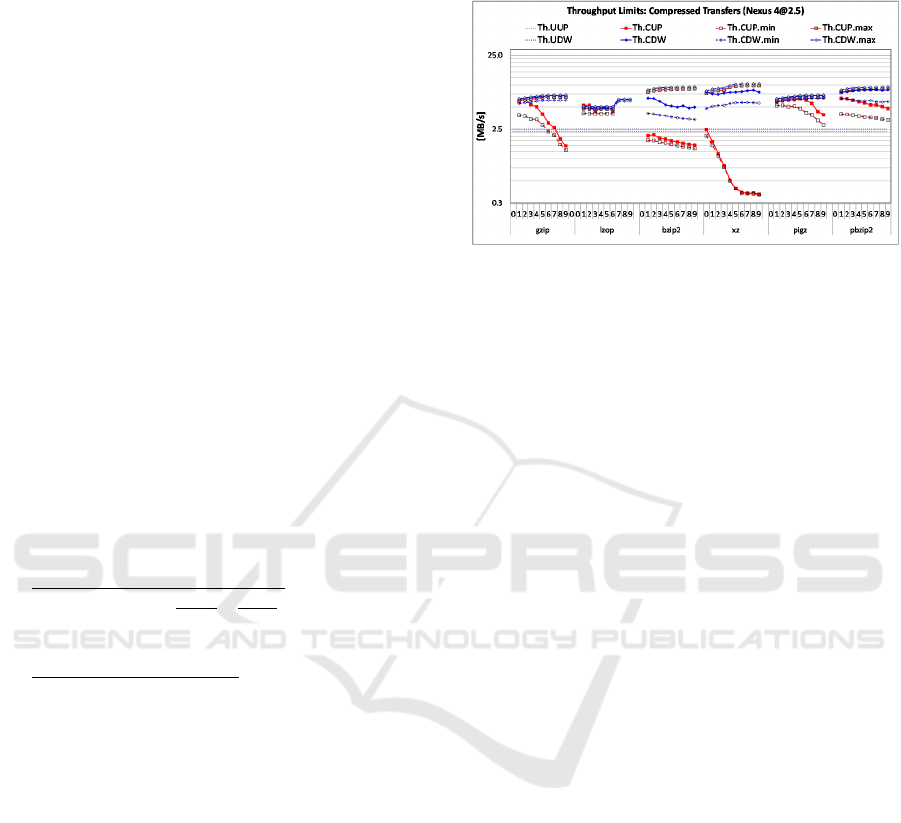
Figure 4 illustrates the estimated minimum and
maximum throughputs, Th.CUP.min [Th.CDW.min]
and Th.CUP.max [Th.CDW.max], respectively, as
well as the measured compressed upload and
download throughput, Th.CUP [Th.CDW], for
different modes of compressed file transfer. The
measurements are performed on a Nexus 4
smartphone with a 2.5 MB/s WLAN network
interface, Th.UP [Th.DW] =2.5 MB/s.
Figure 4: Effective compressed upload and download
throughputs.
For upload, the estimated lower and upper limits
for the compression throughput of gzip -1 are 3.9
MB/s and 6.2 MB/s, and the measured compression
throughput is 5.9 MB/s; in contrast, the estimated
bounds for bzip2 -1 are 1.8 MB/s and 8.1 MB/s and
the measured compression throughput is 2.04 MB/s.
The measured compressed upload throughput is
between the predicted minimum and maximum
throughputs. In cases when the local compression
throughput, Th.C, falls below the network
connection upload throughput, Th.UP, the effective
compressed upload throughput is closer to the
minimum throughput (e.g., for xz). In cases when
Th.C >> Th.UP, the effective compressed upload
throughput is closer to the expected maximum
throughput (e.g, for lzop).
For download, the estimated lower and upper
boundaries for the decompression throughput of
gzip -9 are 6.19 MB/s and 7.29 MB/s, and the
measured compression throughput is 7.16 MB/s. The
utilities with high local decompression throughputs
achieve the effective download throughputs close to
the upper boundaries when downloading large files
(e.g., gzip and lzop for all compression levels).
4.2 Energy Limits
The maximum energy for compressed upload shown
in Equation (18), ET.CUP.max, includes the energy
to perform the local compression of the file on the
mobile device, the energy to setup network
connection, ET.SC, and the energy to transfer the
compressed file, ET.CUP'. The energy to transfer
the compressed file can be calculated as the
compressed file size, US/CR, divided by the energy
efficiency of the network connection for uploads,
EE.UP. The energy to perform local compression on
Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing
47
a mobile device, ET.C, can be used to determine the
local compression energy efficiency, EE.C, defined
as the uncompressed file size, US, divided by the
energy to perform a local compression, ET.C. This
metric captures the mobile device’s ability to
perform compression with the least amount of
energy. The minimum energy for uploads shown in
Equation (19), ET.CUP.min, includes the energy
overhead to perform the local compression of the
file on the mobile device, ET.C(0), the energy to
setup network connection, ET.SC, and the energy to
transfer the compressed file of size, ET.CUP', which
is calculated as described above. The energy
overhead, ET.C(0), excludes the energy needed to
run the platform when idle.
.....′
(18)
...
0
..
(19)
..
∙.
1∙.∙
1
.
.
(20)
..
∙.
1∙.∙
1
.0
.
(21)
The minimum upload energy efficiency,
EE.CUP.min, is calculated as the uncompressed file
size in megabytes, US, divided by the maximum
energy to perform compressed upload, ET.CUP.max.
The maximum upload energy efficiency,
EE.CUP.max, is calculated as the uncompressed file
size in megabytes, US, divided by the minimum
energy to perform compressed upload, ET.CUP.min.
The final expressions in Equations (20) and (21)
show the boundaries for the compressed upload
energy efficiencies as a function of the energy-based
network parameters, EE.UP, ET.SC, file size, US,
compression ratio, CR, and the local compression
energy efficiency, EE.C.
.....′
(22)
...
0
.
.
(23)
..
∙.
1∙.∙
1
.
.
(24)
..
∙.
1∙.∙
1
.0
.
(25)
The maximum energy for compressed downloads
shown in Equation (22), ET.CDW.max, includes the
energy to setup network connection, ET.SC, the
energy to transfer the compressed file, ET.CDW',
and the energy to perform the decompression of the
received file on the mobile device. The energy to
transfer the compressed file can be calculated as the
compressed file size, US/CR, divided by the network
connection download energy efficiency EE.DW. The
energy to perform decompression on the mobile
device, ET.D, can be used to determine the local
decompression energy efficiency, EE.D, which is
defined as the uncompressed file size, US, divided
by the energy to perform decompression. This
metric thus captures the mobile device’s ability to
effectively perform decompression. The minimum
energy for download shown in Equation (23),
ET.CDW.min, includes the energy to setup network
connection, ET.SC, and the energy to transfer the
compressed file, ET.CDW', and the overhead energy
to perform decompression, ET.D(0).
The minimum effective compressed download
energy efficiency, EE.CDW.min, is calculated as the
uncompressed file size in megabytes, US, divided by
the maximum energy to perform the compressed
download, ET.CDW.max. The maximum download
energy efficiency, EE.CDW.max, is calculated as the
uncompressed file size in megabytes, US, divided by
the minimum energy to perform the compressed
download, ET.CDW.min. The final expressions in
Equations (24) and (25) show the boundaries for the
compressed download energy efficiencies as a
function of the network parameters, file size,
compression ratio, and the local decompression
energy efficiency.
Figure 5: Effective compressed upload and download
energy efficiency.
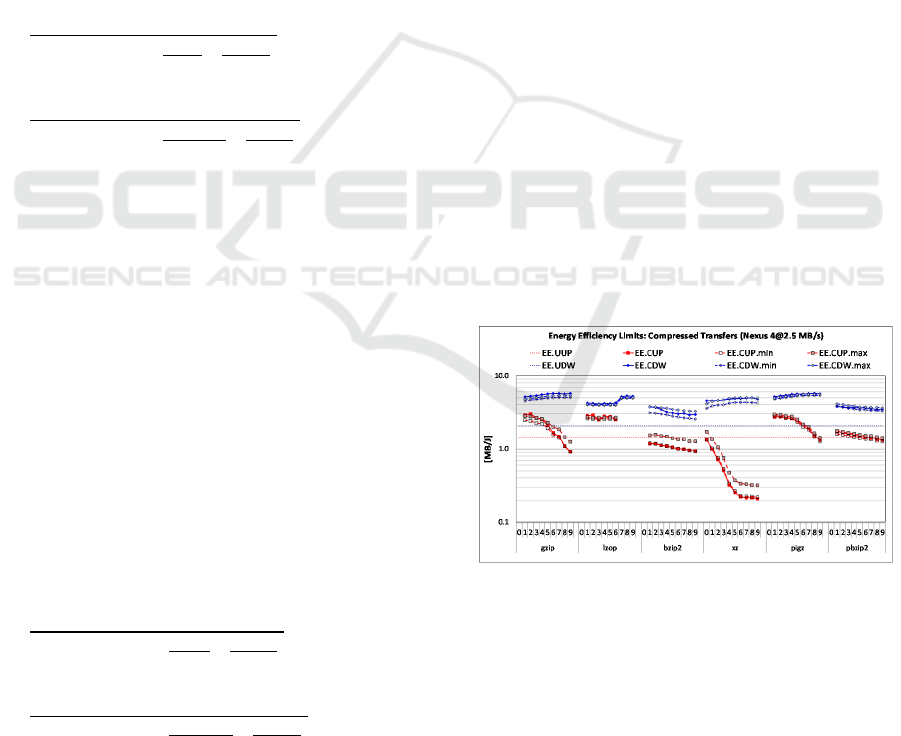
Figure 5 illustrates the estimated energy
efficiency boundaries, EE.CUP.min [EE.CDW.min]
and EE.CUP.max [EE.CDW.max], and the measured
compressed upload and download energy efficiency,
EE.CUP [EE.CDW], for different modes of
compressed file transfer. The measurements are
performed on Nexus 4 smartphone with a 2.5 MB/s
WLAN network interface.
PEC 2016 - International Conference on Pervasive and Embedded Computing
48

For example, the estimated lower and upper
limits for the compression energy efficiency of
gzip -1 are 2.46 MB/J and 2.8 MB/J, and the
measured compression energy efficiency is
2.9 MB/J. The estimated lower and upper boundaries
for the decompression energy efficiency of gzip -9
are 5.06 MB/J and 5.36 MB/J, and the measured
compression energy efficiency is 5.72 MB/J. In both
cases, the utilities with high local (de)compression
energy efficiencies achieve the effective energy
efficiencies close to the upper boundaries when
transferring large files (e.g., gzip and lzop for all
compression levels).
4.3 Piping Model
Whereas we experimentally verified that we can
estimate the minimum and maximum compressed
transfer throughputs and energy efficiencies, the
distance between these boundaries for a particular
compression mode is often too wide, rendering them
insufficient to estimate the effective throughputs or
energy efficiencies. Ideally, we would like to be able
to devise models for accurate estimation of effective
upload and download throughputs and energy
efficiencies.
The use of piping when transferring data file is
beneficial as it increases the effective throughput
and energy efficiency. It allows for overlapping
local (de)compression tasks with the file transfer
tasks on mobile devices. In a case of compressed
upload, a degree of this overlap depends on the ratio
between the network upload throughput or energy
efficiency, Th.UP [EE.UP], and the local
compression throughput or energy efficiency, Th.C
[EE.C]. When the local compression throughput or
energy efficiency exceeds by far the corresponding
network upload throughput, the bottleneck is the
network. When the local compression throughput or
energy efficiency falls below the corresponding
network throughput, the compressed upload is not
beneficial. In a case of compressed downloads, a
degree of overlapping depends on the ratio between
the network download throughput or energy
efficiency, Th.DW [EE.DW], and the local
decompression parameter, Th.D [EE.D].
..
.
.
,..
1,..
(26)
..
∙.
1∙.∙
..
.
.
(27)
..
.
.
,..
1,..
(28)
..
∙.
1∙.∙
..
.
.
(29)
To derive the piping model for upload throughput,
the compression term from the lower throughput
limit is restricted using a corrective factor, described
in Equation (26). This factor lowers the impact of
the local compression term when the local
compression throughput exceeds the network
connection upload throughput. The final model for
the compressed upload throughput with the use of
piping is expressed in Equation (27). To derive the
piping model for download throughput, the
decompression term from the lower throughput limit
is restricted using a corrective factor, described in
Equation (28). The final model for compressed
download throughput is shown in Equation (29).
To derive the piping model for upload energy
efficiency, the compression term from the lower
energy efficiency limit is restricted using a
corrective factor, described in Equation (30). To
derive the piping model for the download energy
efficiency, the decompression term from the lower
energy efficiency limit is restricted using a
corrective factor, as described in Equation (32).
Effectively, the corrective factors restrict the energy
component of the local (de)compression that
includes the energy needed to run the platform,
which is ET.CET.C(0) for compression and
[ET.DET.D(0)] for decompression. The final
models for the compressed upload and download
energy efficiencies with piping are expressed in
Equations (31) and (33), respectively.
..
.
.
,..
1,..
(30)
..
∙.
1∙.∙
..
.
1..
.
0
.
(31)
..
.
.
,..
1,..
(32)
..
∙.
1∙.∙
..
.
1..
.
0
.
(33)
Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing
49
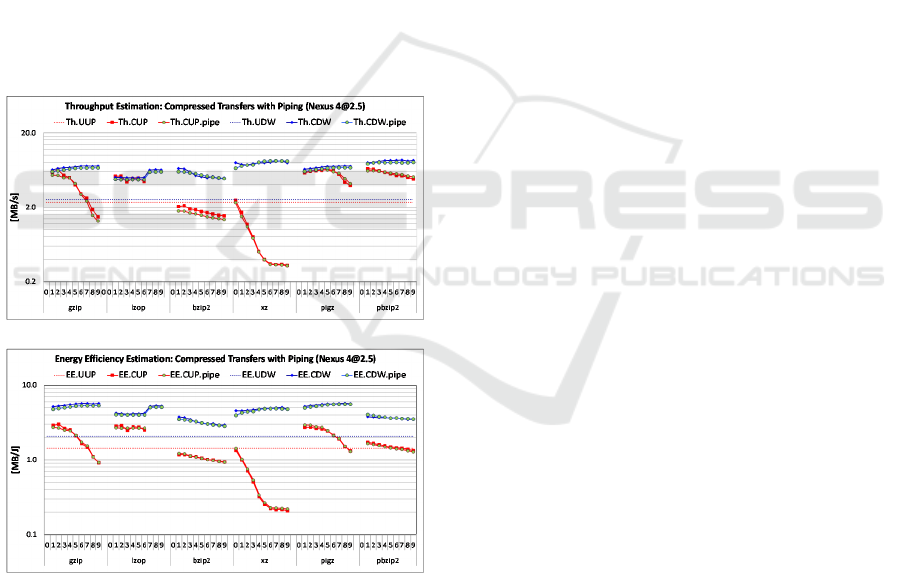
Figure 6(a) shows the estimated compressed upload
(green dots) and download (green circles)
throughput and the measured compressed upload
(red squares) and download (blue triangles)
throughput for all considered compression modes.
Figure 6(b) shows the estimated compressed upload
and download energy efficiency and the measured
compressed upload and download energy
efficiencies for all considered compression modes.
The plots suggest a very high accuracy of the
proposed models for all compression utilities and
compression levels. This expression implies that if
we know the parameters of the network connection
(Th.UP [Th.DW] and T.SC or EE.UP [EE.DW] and
ET.SC), and if for a given uncompressed file of size
US we can predict the compression ratio, CR, and
local compression or decompression throughput or
energy efficiency for a given (utility, level) pair
(Th.C [Th.D] or EE.C [EE.D]) on a particular
mobile device, we can fairly accurately estimate the
expected compressed upload or download
throughput and energy efficiency.
a.
b.
Figure 6: Compressed Upload and Download with piping:
Throughput (a) and Energy Efficiency (b) Estimation.
The proposed models rely on three sets of
parameters: those that are readily available (e.g., file
size), those that can be determined using simple
experiments (T.SC [ET.SC], Th.UP [EE.UP],
Th.DW [EE.DW]), and those that are unknown such
as the compression ratio, CR, and compression or
decompression throughput, Th.C [Th.D], or energy
efficiency, EE.C [EE.D]. To be able to successfully
apply and use the proposed models, the compression
ratio, and the time or energy spent to perform
(de)compression of files has to be estimated. One
method which can provide estimation for
compression ratio and (de)compression throughput
and energy efficiency is the use of data tables filled
with historical data of prior data transfers and their
effectiveness for specific utility-level pairs.
5 CONCLUSIONS
This paper introduces analytical models for
characterizing effective throughput and energy
efficiency of uncompressed and compressed data
transfers between mobile devices and the cloud. We
have demonstrated the validity of the models
through the series of tests conducted on two state-of-
the-art smartphones.
Using the proposed analytical models, we can
initiate the development of frameworks for
optimizing data transfers between mobile devices
and the cloud. The framework can be designed to be
conscientious of the mobile device’s energy status
and network conditions, the user’s history of data
transfers (type and size of files transfers, frequency
of transfers), and the file characteristics, available
compression utilities and their performance.
ACKNOWLEDGEMENTS
This work has been supported in part by National
Science Foundation grants CNS-1205439 and CNS-
1217470.
REFERENCES
Agababov, V., Buettner, M., Chudnovsky, V., Cogan, M.,
Greenstein, B., McDaniel, S., Piatek, M., Scott, C.,
Welsh, M., Yin, B., 2015. Flywheel: Google’s Data
Compression Proxy for the Mobile Web, in:
Proceedings of the 12th USENIX Conference on
Networked Systems Design and Implementation,
NSDI’15. USENIX Association, Berkeley, CA, USA,
pp. 367–380.
Amazon, 2015. What Is Amazon Silk? - Amazon Silk
[WWW Document]. URL http://docs.aws.amazon.
com/silk/latest/developerguide/ (accessed 12.6.15).
Barr, K., Asanović, K., 2003. Energy aware lossless data
compression, in: Proceedings of the 1st International
Conference on Mobile Systems, Applications and
PEC 2016 - International Conference on Pervasive and Embedded Computing
50

Services (MobiSys’03). ACM Press, pp. 231–244.
doi:10.1145/1066116.1066123.
Barr, K.C., Asanović, K., 2006. Energy-aware lossless
data compression. ACM Trans. Comput. Syst. 24, 250–
291. doi:10.1145/1151690.1151692.
CISCO, 2015. Cisco Visual Networking Index: Global
Mobile Data Traffic Forecast Update 2014–2019
White Paper.
Dzhagaryan, A., Milenkovic, A., 2015. On Effectiveness
of Lossless Compression in Transferring mHealth
Data Files, in: 2015 IEEE 17th International
Conference on E-Health Networking, Applications and
Services (Healthcom). Presented at the 2015 IEEE
17th International Conference on e-Health
Networking, Applications and Services (Healthcom),
Boston, MA.
Dzhagaryan, A., Milenković, A., Burtscher, M., 2015.
Quantifying Benefits of Lossless Compression
Utilities on Modern Smartphones, in: 2015 24th
International Conference on Computer
Communication and Networks (ICCCN). Presented at
the 2015 24th International Conference on Computer
Communication and Networks (ICCCN), Las Vegas,
NV.
Dzhagaryan, A., Milenkovic, A., Burtscher, M., 2013.
Energy efficiency of lossless data compression on a
mobile device: An experimental evaluation, in:
Performance Analysis of Systems and Software
(ISPASS), 2013 IEEE International Symposium on.
Austin, TX, pp. 126–127. doi:10.1109/ISPASS.2013.
6557156.
Dzhagaryan, A., Milenkovic, A., Milosevic, M., Jovanov,
E., 2016. An Environment for Automated Measuring
of Energy Consumed by Android Mobile Devices, in:
6st International Conference on Pervasive and
Embedded Computing and Communication Systems
(PECCS). Lisbon, Portugal.
Google, 2014a. Data Server - Google Chrome [WWW
Document]. URL https://developer.chrome.com/
multidevice/data-compression (accessed 10.30.15).
Google, 2014b. About Attachment Manager [WWW
Document]. URL http://www.google.com/support/
enterprise/static/postini/docs/admin/en/admin_msd/att
ach_overview.html (accessed 10.31.15).
Google, 2014c. Nexus - Google [WWW Document]. URL
http://www.google.com/intl/all/nexus (accessed
6.15.14).
Milenkovic, A., Dzhagaryan, A., Burtscher, M., 2013b.
Performance and Energy Consumption of Lossless
Compression/Decompression Utilities on Mobile
Computing Platforms, in: 2013 IEEE 21st
International Symposium on Modeling, Analysis
Simulation of Computer and Telecommunication
Systems (MASCOTS). Presented at the 2013 IEEE
21st International Symposium on Modeling, Analysis
Simulation of Computer and Telecommunication
Systems (MASCOTS), San Francisco, CA, pp. 254–
263. doi:10.1109/MASCOTS.2013.33.
Onavo, 2015. Onavo [WWW Document]. Onavo. URL
http://www.onavo.com (accessed 12.1.15).
OnePlus, 2015. OnePlus One [WWW Document]. URL
https://oneplus.net/one (accessed 7.12.15).
Snappli, 2014. Snappli [WWW Document]. URL
http://snappli.com/ (accessed 12.1.15).
zlib, 2015. zlib Home Site [WWW Document]. URL
http://www.zlib.net/ (accessed 12.16.15).
Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing
51
