An Enhanced Equivalence Checking Method to Handle Bugs in

Programs with Recurrences

Sudakshina Dutta and Dipankar Sarkar

Indian Institute of Technology Kharagpur, Kolkata, India

Keywords:

Equivalence Checking, Recurrence, Dependence, Narrowing.

Abstract:

Software designers often apply automatic or manual transformations on the array-handling source programs

to improve performance of the target programs. Verdoolaege et al. (Verdoolaege et al., 2012) have proposed

a method to automatically prove equivalence of the output arrays of the source and the generated transformed

programs. Unlike the other approaches, the method of (Verdoolaege et al., 2012) provides the most sophis-

ticated techniques to validate programs with non-uniform recurrences besides programs with uniform recur-

rences. However, if the recurrence expressions of the source and the transformed programs refer to more than

one base cases of which some are non-equivalent and also if the domain of the output arrays partition based on

dependences on different base cases, then some imprecision in the equivalence checking results is observed.

The equivalence checker reports that the entire index spaces of the output arrays of the source program to be

non-equivalent with that of the transformed program instead of the portion of the output arrays which depend

on the non-equivalent base cases of the programs. In the current work, we have enhanced the method of equiv-

alence checking of (Verdoolaege et al., 2012) so that it can precisely indicate the equivalent and non-equivalent

portions of the output arrays.

1 INTRODUCTION

Due to resource constraints of embedded processors,

developers apply aggressive loop and data transfor-

mations on the source program and generate the tar-

get program. With the increase of usages of embed-

ded processors in high performance computing sys-

tem, there is a growing need to verify the correct-

ness of such transformations which are primarily ap-

plied by compilers. For validation of such transforma-

tions, dependence graph (DG) oriented mechanisms

are more suitable than the control graph oriented ones

because the domain of applications of such transfor-

mations involve arrays and the dependence compu-

tations of some array elements on other elements.

Unlike the previously reported methods (Shashidhar

et al., 2005), (Karfa et al., 2011), the DG oriented

mechanism reported in (Verdoolaege et al., 2012) has

been found to be sophisticated enough to handle many

loop transformations with recurrences and it is ap-

plied for the case of programs with static control ﬂow

and piecewise afﬁne expressions for all loop bounds,

conditions and array index expressions.

However, if the recurrence expressions of the

source and the transformed programs refer to more

than one base cases some of which are non-equivalent

and also if the domain of the output arrays parti-

tion based on dependences on different base cases,

then equivalence checking mechanism fails to report

non-equivalent portion of the output arrays precisely.

The equivalence checker instead reports that the en-

tire index spaces of the output arrays of the source

program to be non-equivalent with that of the trans-

formed program. Although the problem of formally

verifying programs is undecidable, we have enhanced

the method of equivalence checking of (Verdoolaege

et al., 2012) so that it can precisely indicate the equiv-

alent and non-equivalent portions of the output ar-

rays for the programs with linear recurrences. From

the program, the recurrence expression is extracted

and it is solved for both the equivalent and non-

equivalent base cases to form generalized conjectures

of “proved” (equivalent) and “not proved” (not equiv-

alent) cases. Later the conjectures are proved follow-

ing the equivalence checking mechanism reported in

(Verdoolaege et al., 2012).

254

Dutta, S. and Sarkar, D.

An Enhanced Equivalence Checking Method to Handle Bugs in Programs with Recurrences.

In Proceedings of the 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering (ENASE 2016), pages 254-259

ISBN: 978-989-758-189-2

2 MOTIVATION

Consider the example in Fig. 1. In this example,

two non-equivalent programs with recurrences are

shown where the output arrays in the programs are

D. The only difference in the two programs are in the

assignment statements s

and s

. The elements of the

output array D are non-equivalent if the iterator value

is even, else they are equivalent. However, the tool

(isa-0.12) available with (Verdoolaege et al., 2012)

reports the following:

Equivalence proved: {D[3]}

Equivalence NOT proved: {D[i] : 4 ≤ i ≤ N}

Although the tool reports above equivalence results,

the algorithm of (Verdoolaege et al., 2012) theroti-

cally returns the following results:

Equivalence NOT proved: {D[i] : 3 ≤ i ≤ N}

The above line indicates that equivalence cannot

be proved for the entire range of iterator values

3 ≤ i ≤ N. To remove this imprecision in the output

of the equivalence checker, we have enhanced the

method of (Verdoolaege et al., 2012) in the present

work. The output of the enhanced equivalence

checker is the following:

Equivalence proved: {D[i] : 3 ≤ i ≤ N and ∃α s.t.

i = 2α +1}

Equivalence NOT proved: {D[i] : 3 ≤ i ≤ N and

∃α s.t. i = 2α}

: A[1] = 2

: A[2] = 3

do i = 3, N

: A[i] = 2 ∗ A[i −2]

: A[1] = 2

: A[2] = 9

do i = 3, N

: A[i] = 2 ∗ A[i −2]

(a) (b)

: D[i] = A[i]

end do

: D[i] = A[i]

end do

Figure 1: Two non-equivalent code snippets.

3 MODEL OF EQUIVALENCE

CHECKING

A dependence graph is a connected labeled directed

graph G = hV, E, I, V

i with vertices V , each of which

involves a single arithmetic operation f of a statement

s of the program, and edges E, called dependences

among the vertices (or more precisely, their opera-

tions). There is a set of vertices V

∈ V with in-degree

0 corresponding to an output array and a set I ⊂ V

of vertices corresponding to input arrays, each with

out-degree 0. A vertex v is associated with the iter-

ation domain D

of the surrounding loop (if any) of

the corresponding statement of the program. An edge

e = hv

, v

i starts from a vertex v

and ends in a ver-

tex v

of the DG and is associated with a mapping M

from some subset of domain D

to the subset of the

domain D

capturing the dependence of the operation

f of v

on the value of the operation f of v

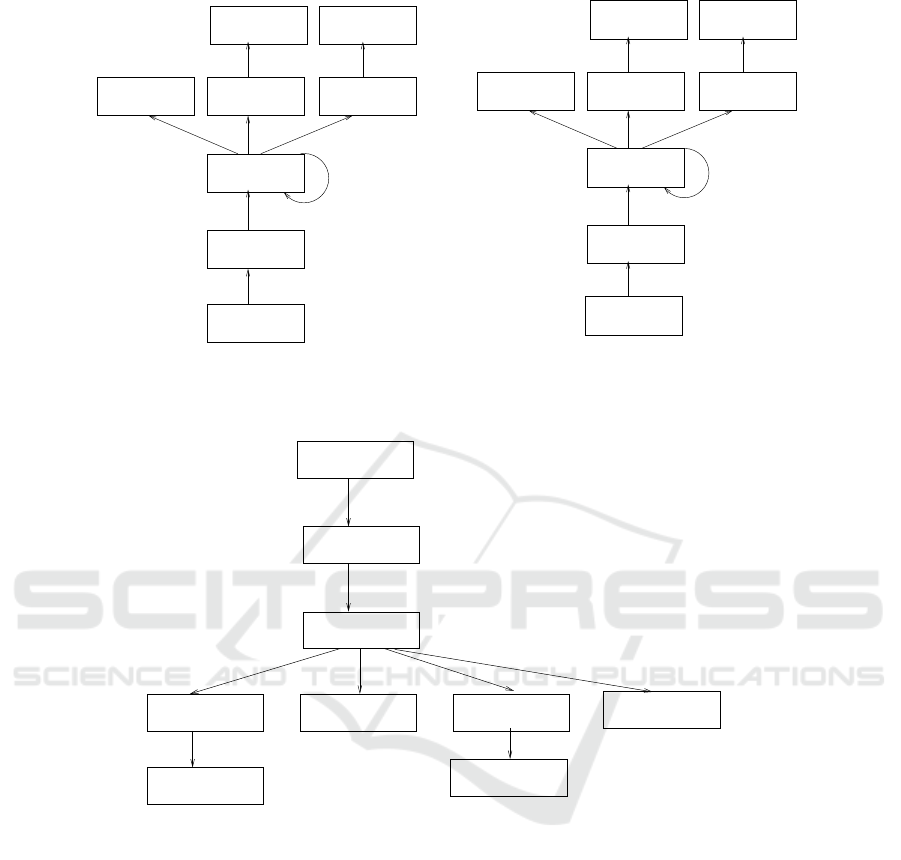
In Fig. 2, the DGs of the the code snippets of Fig. 1

are shown. In Fig. 2(a), v

, v

, ···, v

depict the

vertices of the DG and hv

, v

i, hv

, v

i, etc. represent

some of the edges of the DG. The output vertex v

indicates the output array D of the program. The ver-

tices v

, v

and v

represent the input vertices and they

represent the reference to the constant values of the

array Z in statements s

, s

and s

, respectively. The

id operations in vertices v

, v

represent copy op-

erations in statements s

, s

and s

, respectively. The

domains of the vertices are indicated beside the ver-

tices. As the assignment s

is executed inside the loop

with iteration domain 3 ≤ i ≤ N, the domain of the

vertex v

is indicated as [3, N]. The edges represent

the read after write dependence among the domain el-

ements of the vertices of the DG and it is represented

by the mapping of the edges. The edge hv

, v

i repre-

sents that the i

iteration of the assignment statement

reads the value assigned to the i

iteration of the

statement s

if 3 ≤ i ≤ N. The self-loop hv

, v

i repre-

sents the recurrence present in the statement s

; con-

sequently, the mapping {v

(i) → v

(i −2)|5 ≤ i ≤ N}

depicts the dependence of the i

iteration of the sec-

ond argument of the multiplication operation on the

value generated by the (i − 2)

iteration of the left

hand side of the same operation. The edges hv

, v

and hv

, v

i depict the dependence on the 3

and 4

iterations of the multiplication operation of s

on the

assignment operations of the statements s

and s

The edge hv

, v

i depicts the dependence of the ﬁrst

argument of the multiplication operation on the con-

stant C

for the domain [3, N].

4 OVERVIEW OF THE EXISTING

VALIDATION METHOD

The method of checking equivalence of two programs

(Verdoolaege et al., 2012) takes two DGs as inputs. It

starts by pairing up the output array vertices of the two

DGs and associating with the pair a goal which as-

serts that the elements of the output arrays have to be

pairwise computed identically in both the programs.

These correspondences are maintained in an equiva-

lence tree (ET) which is dynamically constructed as

the equivalence proof proceeds. The goal propagates

as a predicate R

want

in a lockstep fashion along the

pair of edges of DGs until the input vertices of the

DGs are encountered or the pair of vertices recur in

An Enhanced Equivalence Checking Method to Handle Bugs in Programs with Recurrences

255

(i) → v

(2)|3 ≤ i ≤ N}

(i) → v

(2)|3 ≤ i ≤ N}

Out : D

, C

, id

, C

: v

() → v

(2)}

() ()

()

(3) → v

()}

, id

, ∗

[3, N]

(4) → v

()}

(i) → v

(i − 2)|5 ≤ i ≤ N}

(i) → v

(i)|3 ≤ i ≤ N}

[3, N]

Out : D

, C

, id

, C

: v

() → v

(2)} {v

() → v

(9)}

() ()

()

(3) → v

()}

, id

, ∗

[3, N]

(4) → v

()}

(i) → v

(i − 2)|5 ≤ i ≤ N}

[3, N]

() → v

(3)}

(a)

(b)

[3, N]

(i) → v

(i)|3 ≤ i ≤ N}

[3, N]

(i) → v

(i)|3 ≤ i ≤ N}

(i) → v

(i)|3 ≤ i ≤ N}

Figure 2: (a)DG of the program in Fig. 1(a), (b)DG of the program in Fig. 1(b).

↔ v

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

want

= {v

(2) ↔ v

(2)|3 ≤ i ≤ N}

↔ v

lost

= {v

(4) ↔ v

(4)}

↔ v

want

= {v

(i − 2) ↔ v

(i − 2)|5 ≤ i ≤ N}

lost

want

= {v

(2) ↔ v

(2)}

lost

↔ v

i n

↔ v

want

= {v

() ↔ v

()}R

want

= {v

() ↔ v

()} = R

lost

want

= {v

(3) ↔ v

(9)} = R

lost

↔ v

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

↔ v

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

i = 4

i = 3

Figure 3: ET of the DGs shown in Fig. 2.

the ET. A subgoal is discharged as proved when re-

duced to an equivalence between the same elements

of the input arrays. As forward propagation of goals

stops, what cannot be proved as a predicate R

lost

propagated backwards and ﬁnally the subpart of what

cannot be proved is shown with respect to the domains

of the output arrays.

The ET construction process takes the DGs cor-

responding to Fig. 2 as inputs and starts with a root

node n

= hv

, v

i in Fig. 3. The node is associated

with the predicate R

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

which represents the goal that the entire index spaces

of the output arrays are pairwise identical. This goal

propagates from vertices along the edges of the DGs.

In this example, v

has the only outgoing edge hv

, v

and the entire domain v

(i) maps to v

(i), 3 ≤ i ≤ N.

Also, v

has the only outgoing edge hv

, v

i the en-

tire domain v

(i) maps to v

(i), 3 ≤ i ≤ N. Hence,

the goal propagates to the newly constructed node

= hv

, v

i with the goal R

want

= {v

(i) ↔ v

(i)|3 ≤

i ≤ N}.

The goal, R

want

, forward propagates following the

mapping of the DG-edges as stated above. For prov-

ing equivalence of the output arrays D[i], 3 ≤ i ≤ N,

the equivalence of A[i], 3 ≤ i ≤ N has to be established

due to the presence of the assignment statements s

and s

. The values of A[i], 3 ≤ i ≤ N, are determined

by the multiplication operations of the statements s

and s

. Hence, the goal of proving equivalence of

D[i], 3 ≤ i ≤ N boils down to the goal of proving the

ENASE 2016 - 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering

256

(a)

(b)

↔ v

want

= {v

() ↔ v

()}

want

= {v

(2) ↔ v

(2)}

lost

↔ v

want

= {v

(2) ↔ v

(2)}R

want

= {v

(2) ↔ v

(2)}

lost

↔ v

want

= {v

(i − 2) ↔ v

(i − 2)|5 ≤ i ≤ N}

= {v

(i) ↔ v

(i)|3 ≤ i ≤ (N − 2)}

lost

= {v

(4) ↔ v

(4)}

↔ v

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

lost

= {v

(4) ↔ v

(4)}

↔ v

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

↔ v

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

want

= {v

(i) ↔ v

(i)|i = 3 ∧ 5 ≤ i ≤ N}

lost

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

↔ v

lost

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

↔ v

lost

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

want

= {v

(i) ↔ v

(i)|i = 3 ∧ 5 ≤ i ≤ N}

= R

lost

= {v

(6) ↔ v

(6)}

Figure 4: (a) ET of the DGs shown in Fig. 2 after the ﬁrst narrowing, (b) ET of the DGs shown in Fig. 2 after the second

narrowing (narrowed nodes in both the ﬁgures are shown in blue color).

result of the these multiplication operations for the

range 3 ≤ i ≤ N and it is depicted by the ET-node

= hv

, v

i with R

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}.

The equivalence of A[i], 3 ≤ i ≤ N in statements s

and s

can only be established if the equivalence of

A[i − 2], 3 ≤ i ≤ N can be proved. For i = 3, the

computation of A[i] in the source and the target pro-

grams depend on the base cases denoted by the as-

signment operations of s

in the source program and

in the target program; this is depicted by the equiv-

alence of the constant expressions C

in the ET-node

with R

want

= {v

(2) ↔ v

(2)}. Similarly, for i = 4,

the computation of A[i] depends on the base case de-

noted by the assignment operation depicted by s

the source program and s

in the target program. This

is depicted by the inequivalence of the assignment of

constant expressions C

and C

in the statements s

and s

, respectively in the ET-node n

with R

want

(3) ↔ v

(9)} and R

lost

= R

want

. For 5 ≤ i ≤ N, the

equivalence of A[i] is dependent on the computation

A[i − 2] evaluated in the same statements by multipli-

cation operations due to the presence of recurrences in

statements s

and s

; this is depicted by the node n

However, the equivalence of the entire range A[i − 2],

5 ≤ i ≤ N cannot be established as the inequivalent

assignments A[2] = 3 in s

and A[2] = 9 in s

are re-

ferred for computation of array elements A[4] in the

source and target programs, respectively.

As the array element A[4] is not equivalent in the

source and the transformed program, from the entire

range of A[i], 3 ≤ i ≤ N, the element i = 4 is sepa-

rated (referred to as ﬁrst narrowing operation (Cousot

and Cousot, 1992) in Fig. 4(a)) and the inequivalence

of the elements A[4] is depicted as R

lost

= {v

(4) ↔

(4)}. The process of establishing equivalence starts

for the revised range i = 3 ∧ 5 ≤ i ≤ N. However,

the equivalence of the entire range of the revised goal

cannot also be established as for the range 5 ≤ i ≤ N

the computation of A[6] depends on the computation

of inequivalent array elements A[4] in the source and

target programs. Hence, the entire range of A[i], 3 ≤

i ≤ N is reported to be inequivalently computed and

it results in the inequivalence of D[i], 3 ≤ i ≤ N (re-

ferred to as second narrowing operation in Fig. 4(b)).

Note that the ﬁrst narrowing node n

with revised goal

want

= {v

(i) ↔ v

(i)|i = 3 ∧ 5 ≤ i ≤ N} is installed

in Fig. 4(a) from which the forward propagation starts

once again. After the second narrowing operation, the

entire range of R

want

is set to R

lost

. In the next step,

lost

∪ R

lost

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N} propagates

back to n

and R

lost

is set to {v

(i) ↔ v

(i)|3 ≤ i ≤ N}.

5 SUGGESTED ENHANCEMENT

For proving equivalence of the output arrays D[i], 3 ≤

i ≤ N, the equivalence of A[i], 3 ≤ i ≤ N, has to be es-

An Enhanced Equivalence Checking Method to Handle Bugs in Programs with Recurrences

257

tablished. For i = 3, the array elements A[i] depend on

the base case denoted by the equivalent assgiments of

constant expressions C

on array elements A[1] in the

satements s

and s

. Hence, the array elements A[3]

are equivalently computed. For the i = 4, the array el-

ements A[i] depend on the base case denoted by the in-

equivalent assgiments of constant expressions C

and

on array elements A[2] in the statements s

and

, respectively. Hence, the array elements A[4] are

inequivalently computed. For the rest of the domain

5 ≤ i ≤ N, the computation of A[i] depends on the

computation of A[i − 2] due to recurrence. Instead of

declaring the entire range of A[i], 3 ≤ i ≤ N, to be not

proved to be equivalent in the source and transformed

programs as (Verdoolaege et al., 2012), the recurrence

relation depicted by the index expressions A[i] and

A[i − 2] (i.e., i

= i

m−1

+ 2) are solved for the base

cases i = 3 and i = 4 in our proposed method. The so-

lution of the recurrence relation for i = 3 mapped to

the range 3 ≤ i ≤ N (3 ≤ i ≤ N ∧∃m ≥ 0 s.t. i = 3+2m

i.e., the odd iterator values) is declared as the index

range for which the array elements A[i] are equiva-

lently computed and the solution for i = 4 mapped to

the range (3 ≤ i ≤ N ∧ ∃m ≥ 0 s.t. i = 4+2m i.e., pre-

cisely the even iterator values) is declared as the index

range for which the array elements A[i] are inequiva-

lently computed.

The ET-node n

represents the goal of proving

equivalence of A[i], 3 ≤ i ≤ N, for proving equiva-

lence of D[i], 3 ≤ i ≤ N in Fig. 3. The ET-node n

represents the fact that for proving equivalence of A[i],

5 ≤ i ≤ N, the equivalence of A[i − 2] has to be estab-

lished. The recurrence relations are formed using the

method given below. In Fig. 3, we refer to the sufﬁx

expression i associated with the ancestor node n

and the sufﬁx expression i − 2 associated with its

recurring descendant node n

as i

m−1

thereby produc-

ing the recurrence i

= i

m−1

+ 2; the inequivalence

of the array element A[4] contributes to the base case

= 4 of the above recurrence. Thus, the recurrence

equation {i

= 4, i

= i

m−1

+ 2} depicts the non-

equivalent elements that would occur if we permit

the ET-node n

to reduce further. The solution of the

above-mentioned non-homogeneous recurrence equa-

tion is i

= 4 + 2m; hence, the “not proved” elements

of the ET-node n

is {v

(i) ↔ v

(i)|3 ≤ i ≤ N ∧ ∃m ≥

0 s.t. i = 4+2m}. To represent such elements of n

, a

child n

3,2

is created with R

want

3,2

= {v

(i) ↔ v

(i)|3 ≤

i ≤ N ∧ ∃m ≥ 0 s.t. i = 4 + 2m} thereby setting the

goal of proving equality of all the elements of R

want

3,2

The ET-node n

3,2

is then explored further to disprove

the proof goal R

want

3,2

following the existing method.

The proposed method tries to generalize the

proved cases next from Fig. 3 in a similar way as has

been described above. The recurrence equation {i

3, i

= i

m−1

+ 2} is found using the same steps as de-

scribed in the previous paragraph for the generaliza-

tion of the proof goal for the equivalent base case for

array elements A[3]. It depicts the “proved” elements

that would occur if the ET-node n

is permitted to re-

duce further. The solution of the above-mentioned re-

currence equation is i

= 3 + 2m. Hence, the gener-

alized “proved” elements at the ET-node n

is con-

jectured as {v

(i) ↔ v

(i)|3 ≤ i ≤ N ∧ ∃m s.t. i =

3 + 2m}. A child node n

3,1

of n

is created with

the goal of proving the conjecture, i.e., R

want

3,1

is set

as {v

(i) ↔ v

(i)|3 ≤ i ≤ N ∧ ∃m s.t. i = 3 + 2m} as

shown in Fig. 5. It is explored further to establish

the proof goal R

want

3,1

using the existing method and

lost

3,1

0. In the next step, R

lost

3,2

= {v

(i) ↔ v

(i)|3 ≤

i ≤ N ∧ ∃m ≥ 0 s.t. i = 4 + 2m} propagates back

to root node n

resulting in {v

(i) ↔ v

(i)|3 ≤ i ≤

N ∧ ∃m ≥ 0 s.t. i = 4 + 2m}. This enhancement can

also be used to precisely identify the equivalent and

non-equivalent portions of the output arrays with one

or more than one dimensions for the programs with

linear recurrences and one or multiple base cases.

6 RELATED WORK

We have enhanced a novel, fully automated approach

to the equivalence checking problem of static afﬁne

programs which uses abstract interpetation operator

instead of using transitive closure operators. The two

most closely related approaches are those of (Shashid-

har et al., 2005), and (Karfa et al., 2011). In (Shashid-

har et al., 2005), the authors proposed an ADDG

based equivalence checking method to validate the

loop transformations. The authors of (Karfa et al.,

2011) redeﬁne the equivalence of ADDGs to ver-

ify loop transformations along with a wide range of

arithmetic transformations. The equivalence checking

method relies on a normalization technique proposed

in (Karfa et al., 2011) and some simpliﬁcation rules

to handle arithmetic transformations over arrays. As

explained before, all of these approaches are based on

transitive closures and therefore require uniform re-

currences, unlike the abstract interpretaion based ap-

proach proposed in (Verdoolaege et al., 2012). We

have enhanced the method for the programs with re-

currences and some non-equivalent base cases.

7 CONCLUSION

We have enhanced the most sophisticated method of

ENASE 2016 - 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering

258

↔ v

proved

= {v

(3) ↔ v

(3)}

3,1

3,2

↔ v

want

3,2

= {v

(i) ↔ v

(i)|3 ≤ i ≤ n ∧ ∃m s.t. i = 4 +2m}

want

= {v

() ↔ v

()}R

want

= {v

() ↔ v

()}

↔ v

i hv

↔ v

ihv

↔ v

= R

lost

want

= {v

(3) ↔ v

(9)}

lost

↔ v

want

= {v

(2) ↔ v

(2)}

lost

↔ v

lost

want

= {v

(2) ↔ v

(2)}

want

3,1

= {v

(i) ↔ v

(i)|3 ≤ i ≤ n ∧ ∃ m s.t. i = 3 + 2m}

= R

lost

3,2

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ n}

lost

= {v

(i) ↔ v

(i)|4 ≤ i ≤ N ∧ ∃m s.t. i = 4 + 2m}

↔ v

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

lost

= {v

(i) ↔ v

(i)|4 ≤ i ≤ N ∧ ∃m s.t. i = 4 + 2m}

↔ v

lost

= {v

(i) ↔ v

(i)|4 ≤ i ≤ N ∧ ∃m s.t. i = 4 + 2m}

want

= {v

(i) ↔ v

(i)|3 ≤ i ≤ N}

want

= {v

(2) ↔ v

(2)}

lost

want

= {v

(i − 2) ↔ v

(i − 2)|6 ≤ i ≤ n ∧∃m s.t. i = 6 + 2m}

want

= {v

(i − 2) ↔ v

(i − 2)|5 ≤ i ≤ n ∧ ∃m i = 5 + 2m}

Figure 5: After enahancement, the ﬁnal ET of the DGs shown in Fig. 2 after the forward and backward propagations are over.

checking equivalence of array-handling programs

with recurrences. We are currently incorporating

the method in the source code available with (Ver-

doolaege et al., 2012). The proposed method works

on homogeneous or non-homogeneous linear recur-

rence equtions. Also, we can precisely partition the

domain of the output array to be “proved” and “not

proved” using the method and are able to prove the

generalized conjectures correctly. Unlike the method

of (Verdoolaege et al., 2012), we can prove the “not

proved to be equivalent” elements of the output ar-

rays to be inequivalently computed. The proposed

method has wide applications in signal processing do-

mains where application programs are implemented

with programs having recurrences.

REFERENCES

Cousot, P. and Cousot, R. (1992). Comparing the ga-

lois connection and widening/narrowing approaches

to abstract interpretation. In Proceedings of the 4th

International Symposium on Programming Language

Implementation and Logic Programming, PLILP ’92,

pages 269–295, London, UK, UK. Springer-Verlag.

Karfa, C., Banerjee, K., Sarkar, D., and Mandal, C. (2011).

Equivalence checking of array-intensive programs. In

VLSI (ISVLSI), 2011 IEEE Computer Society Annual

Symposium on, pages 156–161.

Shashidhar, K. C., Bruynooghe, M., Catthoor, F., and

Janssens, G. (2005). Functional equivalence checking

for veriﬁcation of algebraic transformations on array-

intensive source code. In Design, Automation and Test

in Europe, 2005. Proceedings, pages 1310–1315 Vol.

Verdoolaege, S., Janssens, G., and Bruynooghe, M. (2012).

Equivalence checking of static afﬁne programs using

widening to handle recurrences. ACM Trans. Pro-

gram. Lang. Syst., 34(3):11:1–11:35.

An Enhanced Equivalence Checking Method to Handle Bugs in Programs with Recurrences

259