
Extracting Dynamics from Multi-dimensional Time-evolving Data
using a Bag of Higher-order Linear Dynamical Systems
Kosmas Dimitropoulos, Panagiotis Barmpoutis, Alexandors Kitsikidis and Nikos Grammalidis
Information Technologies Institute, Centre for Research and Technology Hellas, Thessaloniki, Greece
Keywords: Linear Dynamical Systems, Human Action Recognition, Dynamic Texture Analysis, Higher Order
Decomposition.
Abstract: In this paper we address the problem of extracting dynamics from multi-dimensional time-evolving data. To
this end, we propose a linear dynamical model (LDS), which is based on the higher order decomposition of
the observation data. In this way, we are able to extract a new descriptor for analyzing data of multiple
elements coming from of the same or different data sources. Each sequence of data is modeled as a
collection of higher order LDS descriptors (h-LDSs), which are estimated in equally sized temporal
segments of data. Finally, each sequence is represented as a term frequency histogram following a bag-of-
systems approach, in which h-LDSs are used as feature descriptors. For evaluating the performance of the
proposed methodology to extract dynamics from time evolving multidimensional data and using them for
classification purposes in various applications, in this paper we consider two different cases: dynamic
texture analysis and human motion recognition. Experimental results with two datasets for dynamic texture
analysis and two datasets for human action recognition demonstrate the great potential of the proposed
method.
1 INTRODUCTION
Machine learning problems often involve sequences
of real-valued multivariate observations. To model
the statistical properties of such data, it is assumed
that each observation is correlated to the value of an
underlying latent variable that is evolving over the
course of the sequence. If the state is real-valued and
the noise terms are assumed to be Gaussian, the
model is called a linear dynamical system (LDS)
(Boots, 2009). Thus, a linear dynamical system is
associated with a first order ARMA process with
white zero means IID Gaussian input (Doretto et al.,
2003). Linear dynamical systems are an important
tool for modeling time series in engineering,
controls and economics, as well as the physical and
social sciences and they have been successfully used
in the past for various vision tasks such as: dynamic
texture analysis, synthesis, segmentation,
registration and categorization (Soatto et al., 2001).
They have also been employed for the categorization
of video sequences in multimedia databases and
more recently in human action recognition tasks.
More specifically, in the field of video
categorization a lot of methods have adopted LDSs
focusing mainly on the definition of a suitable
distance or kernel between the model parameters of
two dynamical systems (Doretto et al., 2003); (Chan
and Vasconcelos, 2005); (Chan and Vasconcelos,
2007); (Vishwanathan et al., 2007). In addition,
Turaga et al., (2011) showed that the parameters of
linear dynamic models are finite dimensional linear
subspaces that can be described using the unified
framework of Grassmann and Stiefel manifolds and
proposed algorithms for supervised and
unsupervised clustering for activity recognition, face
recognition and video clustering. More recently, a
new method was introduced by Ravichandran et al.,
(2013) aiming to model video sequences with a
collection of LDSs, which are then used as features
in a bag of systems approach, while Luo et al.,
proposed the modelling of motion dynamics with
robust LDSs using the model parameters as motion
descriptors.
Nevertheless, a limitation of linear dynamical
systems is that they exploit information from only
one element, i.e., channel, thus, in the case of
multidimensional data the concatenation of different
components into one single element is required. To
this end, in this paper we propose a more efficient
Dimitropoulos, K., Barmpoutis, P., Kitsikidis, A. and Grammalidis, N.
Extracting Dynamics from Multi-dimensional Time-evolving Data using a Bag of Higher-order Linear Dynamical Systems.
DOI: 10.5220/0005844006830688
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 683-688
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
683
way to model dynamics by taking advantage of the
multidimensionality of data. More specifically, we
present a higher-order LDS model in order to extract
a new descriptor for analyzing data coming from
multiple elements, e.g., channels in the case of video
sequences or joint coordinates in the case of skeleton
animation data. The proposed model is based on the
higher order decomposition of the multidimensional
data and enables the analysis of dynamic time-series
using information from the same or different data
sources, e.g., colour visible range cameras, infrared
sensors of various spectral ranges, or even
synthesized images.
The proposed h-LDS descriptors are estimated in
equally sized temporal segments, while a bag of
systems approach is adopted, in which the h-LDSs
are used as feature descriptors. For the formation of
the codebook, a k-medoids (Kaufman and
Rousseeuw, 1987) classification method is applied,
where the K codewords correspond to K
representative higher order LDSs. Each data
sequence is then represented as a Term Frequency
(TF) histogram of the predefined codeword of h-
LDSs and is provided to a SVM classifier.
For evaluating the performance of the proposed
methodology to extract dynamics from time series
and using them for classification, in this paper we
deal with the problems of dynamic texture analysis
and human action recognition.
2 HIGHER-ORDER LINEAR
DYNAMICAL ANALYSIS
2.1 Estimation of the h-LDS Descriptor
As was mentioned above a linear dynamical system
is associated with a first order ARMA process with
white zero mean IID Gaussian input. More
specifically, the stochastic modeling of both
dynamics and appearance is encoded by two
stochastic processes, in which dynamics are
represented as a time-evolving hidden state process
x(t)∈
and observed data y(t)∈
as a linear
function of the state vector:
1
(1)
(2)
where ∈
is the transition matrix of the
hidden state (n is the dimension of hidden state with
n≤d), while ∈
is the mapping matrix of the
hidden state to the output of the system. The
quantities w(t) and Bv(t) are the measurement and
process noise respectively, with w(t)~N(0,R) and
Bv(t)~N(0,Q). The main advantage of the LDS
descriptor ,, is that it contains both the
appearance information of the data segment, which
is modeled by , and its dynamics that are
represented by .
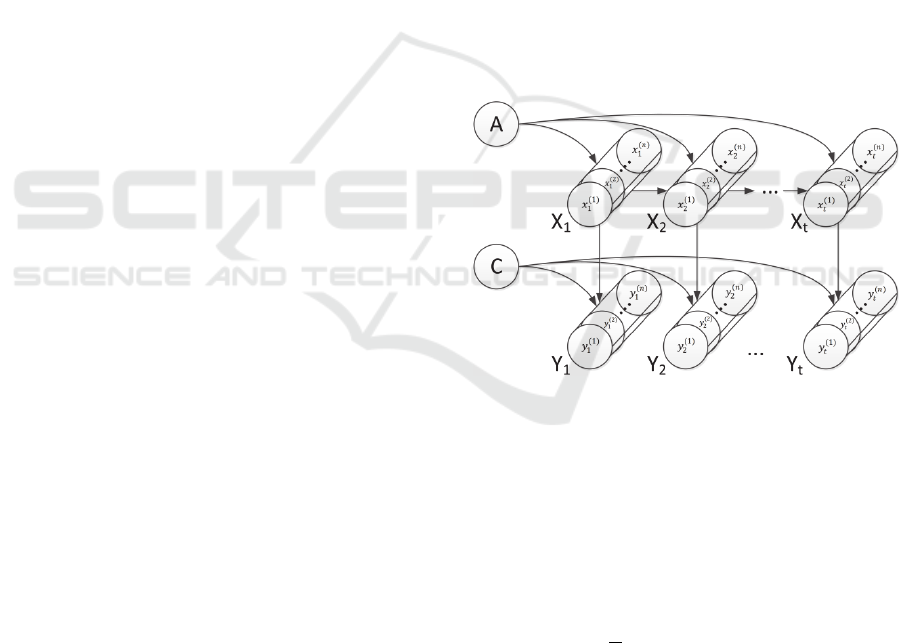
In the case of multidimensional data,
observations can be represented by a tensor Y∈
….
of order n, where d
1
, d
2
,....,d
n
are integer
numbers indicating the number of elements in each
dimension. For instance, if we consider a colour
video sequence of F frames, the order of tensor Y (in
the rest of the paper the term 'tensor' is used to
indicate a matrix of order higher than two) is four,
where d
1
and d
2
indicate the width and height of the
image respectively, d
3
is the number of image
elements (d
3
=3) and d
4
is the number of frames. In
order to estimate the matrices A and C containing the
dynamics and appearance information respectively
(see Figure 1), we need to decompose the n-order
tensor Y, so that the columns of the mapping matrix
C are orthonormal (Doretto et al., 2003).
Figure 1: A graphical representation of the h-LDS model.
To satisfy the aforementioned requirement, we
use the HOSVD (Kuo, 2013), which is a
generalization of the singular value decomposition
for higher order tensors. More specifically, we first
subtract from Y the temporal data average
in order
to construct a zero mean matrix in the time axis,
where the temporal average is computed as:
1
,
,…..,
,
(3)
and then we decompose tensor Y as follows:
…
(4)
where U
(1)
,U
(2)
,....U
(n)
are orthogonal matrices
containing the orthonormal vectors spanning the
column space of the i-mode matrix unfolding Y
(i)
and
RGB-SpectralImaging 2016 - Special Session on RBG and Spectral Imaging for Civil/Survey Engineering, Cultural, Environmental,
Industrial Applications
684

denotes the i-mode product between a tensor and
a matrix (Kuo, 2013), with i=1,2...n. Since, the
choice of matrices A, C and Q in equations (1) and
(2) is not unique, in the sense that there are infinitely
many such matrices that give rise to exactly the
same sample paths starting from suitable initial
conditions (Doretto et al., 2003), we can consider
C=
)(n
U
, where
)(n
U
is an orthogonal matrix and
X=
…
(5)
Hence, equation (4) can be reformulated as follows:
(6)
The n-mode product of tensor X∈
….
with
matrix C∈
can be defined as:
⇔
(7)
The transition matrix A, containing the dynamics of
the multidimensional data, can then be easily
computed by using least squares:
(8)
where the matrices
1
,
2
,…,
1
and
2
,
3
,…,
are formed from the
unfolding X
(n)
of tensor X along the n
th
dimension.
2.2 Codebook Creation and
Classification
For the formation of the codebook, k-medoids
clustering is applied, however, before that we need
to define a similarity metric between two descriptors
,
and
,
that will be
applicable to the non-Euclidean space of h-LDSs.
Since h-LDS descriptor consists of a pair of two-
dimensional matrices, we can easily use as a
similarity metric the Martin distance between
and
:
,
ln
(9)
where θ
i
are the subspace angles (Cock and Moor,
2002) between the two models. The cosine of θ
i
can
be calculated as the square root of the i-th
eigenvalue of the matrix P
P
P
P
:
cos
θ
i
eigenvalue
P
P
P
P
(10)
where the estimation of matrix
2221
1211
PP
PP
P
is performed by solving the Lyapunov equation
A
PAP C
C, where
2
1
0
0
A
A
A
and
21
CCC
The codebook can then be created by using h-LDS
as feature descriptors. Specifically, the training
dataset of the h-LDS descriptors is fed into k-
medoids algorithm for the creation of a codebook of
K codewords corresponding to K representative h-
LDSs, as shown in Figure 2. Finally, each data
segment is then represented as a Term Frequency
(TF) histogram of the predefined codeword of h-
LDSs.
Figure 2: h-LDS codebook creation and classification.
3 EXPERIMENTAL RESULTS
For evaluating the performance of the proposed
methodology to extract dynamics from time
evolving multidimensional data and using them for
classification, in this paper we consider two different
applications: i) dynamic texture analysis and ii)
human motion recognition. In the former case, the
proposed high order LDS descriptor is used to model
the temporal evolution of pixels intensities, while in
the latter the evolution of skeleton joints positions
during the performance of a motion is considered as
a multidimensional time series.
3.1 Dynamic Texture Analysis
In this section we present experimental results using
two video datasets for dynamic texture analysis.
More specifically the first dataset (Dimitropoulos et
al., 2015) contains videos with flame and flame-
Extracting Dynamics from Multi-dimensional Time-evolving Data using a Bag of Higher-order Linear Dynamical Systems
685
colored objects, while the second one contains
videos with smoke and non-smoke frames
(Barmpoutis et al., 2014). In both cases, each frame
of the video sequence is divided into image patches
of size 16x16, which is a typical approach in video-
based fire detection systems and then a pre-
processing step is applied aiming to identify
candidate image patches i.e., patches containing a
sufficient number of flame or smoke colored moving
pixels. To this end, we initially apply an Adaptive
Median algorithm (McFarlane and Schofield, 1995),
(Dimitropoulos et al., 2012), which is fast and very
efficient algorithm for detecting moving pixels, and
then we use a fire probability model (Dimitropoulos
et al., 2015) or a HSV smoke color model
(Avgerinakis et al., 2012) to identify candidate flame
or smoke image patches respectively.
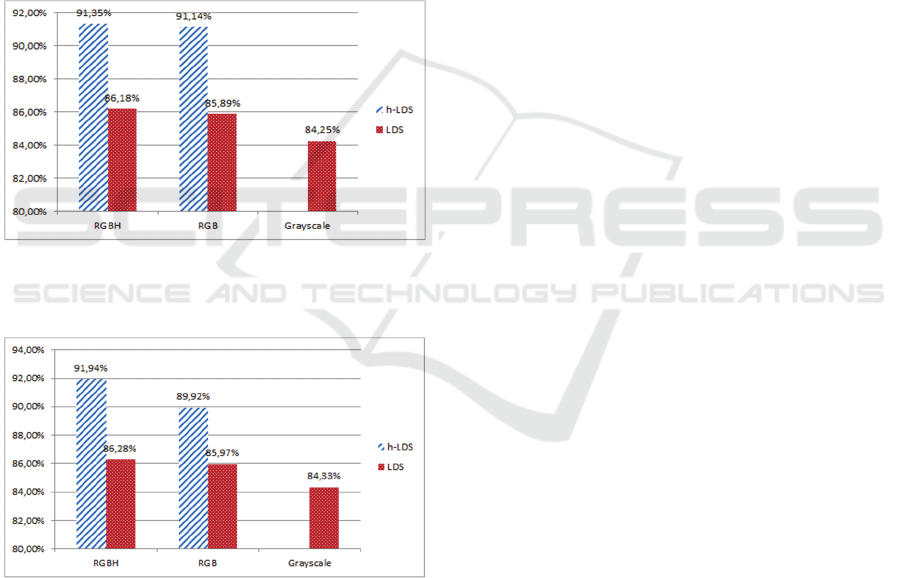
Figure 3: Comparison of LDS and h-LDS with grayscale,
RGB and RGBH data using the dataset containing flame
and flame colored objects.
Figure 4: Comparison of LDS and h-LDS with grayscale,
RGB and RGBH data using the dataset containing smoke
and smoke colored objects.
For each candidate image patch we estimate a h-
LDS descriptor using a temporal length of 16
frames. In addition, for the classification of each
frame, we create histogram representations
corresponding to the sub-sequences of T previous
frames (in our experiments T=100). In the
experimental results, we estimated the number of
correctly detected frames out of the total number of
frames in each dataset. As can be seen in Figures 3
and 4, the proposed descriptor outperforms standard
LDSs in both cases i.e., flame and smoke
identification respectively. In order to validate the
performance of both descriptors with a different
number of elements, apart from the use of grayscale
and RGB data (i.e., three elements), we also created
a fourth channel by visualizing the feature space of
HOG descriptor as in (Vondrick et al., 2013) (i.e.,
RGBH data). Especially in the case of smoke, the
fourth channel seems to improve significantly the
results, while LDS descriptor does not seem to
change significantly its detection rate.
3.2 Human Action Recognition
In this section we deal with the problem of human
action recognition in game-like applications. More
specifically, for capturing the human motion, depth
sensors are used, while the evolution of skeleton
joints positions during the performance of a motion
is considered as a multidimensional time series. To
extract the dynamics of the body motion, we
segment the multidimensional signal into equally
sized elementary segments using a sliding time
window of 16 frames. In this way we accomplish a
better representation of human motion, instead of
using the whole non-linear sequence of data, as each
elementary segment can be efficiently modelled by a
linear dynamical system.
Experimental results with two datasets for human
action recognition show that the proposed method
outperforms the different variants of LDSs on the
recognition task of body motion. More specifically,
for the validation of the proposed method we created
a new Kinect gesture dataset consisting of 360
motions, while we also used a well-known dataset
such as MSRC-12 (Fothergill et al., 2012). More
specifically the new dataset contains 6 actions (bend
forward, left kick, right kick, raise hands, hand
wave, push with hands) performed by 6 subjects,
each repeated 10 times (360 motions in total) and the
Microsoft Research Cambridge-12 Kinect gesture
data set (MSRC-12) comprises of 594 sequences
collected from 30 people performing 12 gestures.
The MSRC-12 dataset is partitioned along different
methods of instruction given to the subjects such as
text and video. We used the part of the dataset where
video only instructions were given. Both datasets
contain tracks of 20 skeleton joint position
coordinates estimated using the Kinect Pose
Estimation pipeline.
RGB-SpectralImaging 2016 - Special Session on RBG and Spectral Imaging for Civil/Survey Engineering, Cultural, Environmental,
Industrial Applications
686
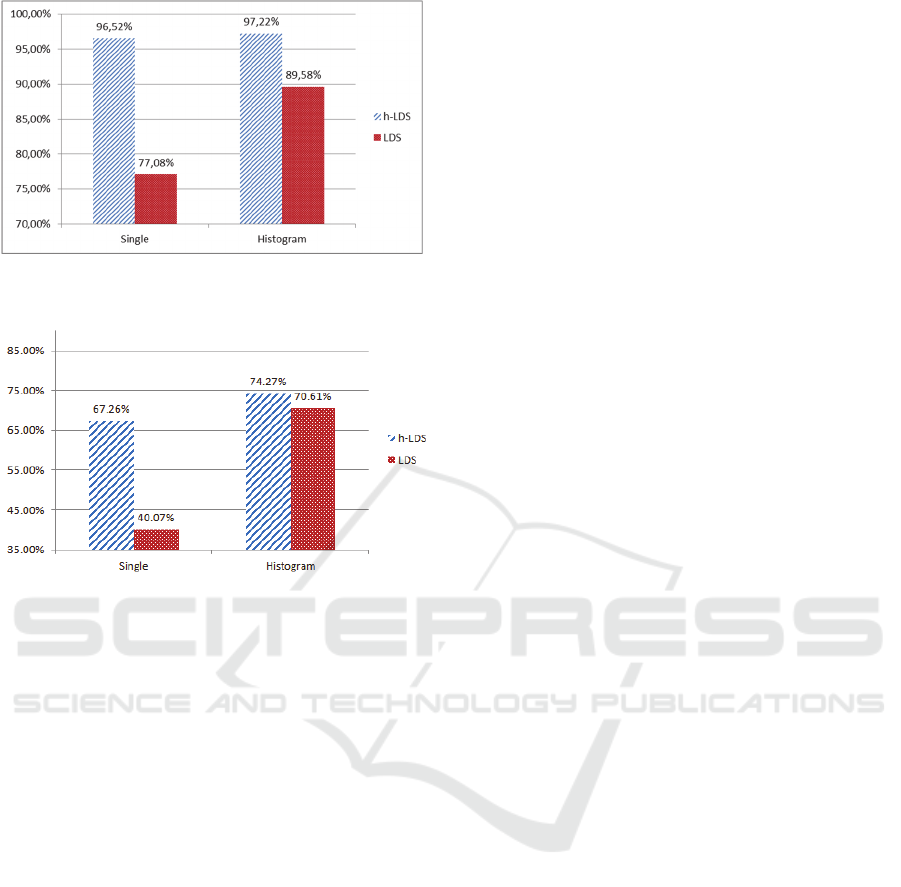
Figure 5: Comparison of LDS and H-LDS descriptor
performance on our dataset.
Figure 6: Comparison of LDS and H-LDS descriptor
performance on MSRC-12 dataset.
As seen in Figures 5 and 6 the histogram of
LDSs offer an improvement in classification results
compared to using a single descriptor for the whole
motion. Additionally, the h-LDS descriptor clearly
outperforms the simple LDS descriptor in each case.
This extends to the case of histogram of LDSs,
where the same behavior can be observed.
4 CONCLUSIONS
In this paper, we introduced a higher order linear
dynamical systems (h-LDS) descriptor for extracting
dynamics from multidimensional time evolving data.
By applying higher order decomposition in the
observation data, we showed that we can achieve
higher detection rates than standard linear dynamical
systems both in the case of dynamic texture analysis
and human action recognition. In the future, we are
planning to use data from different sources, e.g.,
multispectral imaging in the case of flame detection
or skeletal data and depth data in the case of human
action recognition.
ACKNOWLEDGEMENTS
The research leading to these results has received
funding from the European Community's Seventh
Framework Programme (FP7-ICT-2011-9) under
grant agreement no FP7-ICT-600676 ''i-Treasures:
Intangible Treasures - Capturing the Intangible
Cultural Heritage and Learning the Rare Know-How
of Living Human Treasures''.
REFERENCES
Avgerinakis, K., Briassouli, A., Kompatsiaris, I., 2012.
"Smoke Detection Using Temporal HOGHOF
Descriptors and Energy Colour Statistics from Video,"
in Int'l Workshop on Multi-Sensor Systems and
Networks for Fire Detection and Management.
Barmpoutis, P., Dimitropoulos, K., Grammalidis, N.,
2014. "Smoke Detection Using Spatio-Temporal
Analysis, Motion Modeling and Dynamic Texture
Recognition", 22nd European Signal Processing
Conference (EUSIPCO 2014), Lisbon, Portugal, 1-5
September.
Boots, B., 2009. Learning stable linear dynamical systems.
M.S. Thesis in Machine Learning, Carnegie Mellon
University.
Chan, A., Vasconcelos, N., 2005. "Probabilistic Kernels
for the Classification of Auto-Regressive Visual
Processes," in IEEE Conf. Computer Vision and
Pattern Recognition.
Chan, A., Vasconcelos, N., 2007. "Classifying Video with
Kernel Dynamic Textures," in IEEE Conf. Computer
Vision and Pattern Recognition.
Cock, K. D., Moor, B. D., 2002. "Subspace angles and
distances between ARMA models," System and
Control Letters, vol. 4, pp. 265-270.
Dimitropoulos, K., Tsalakanidou, F., Grammalidis, N.,
2012. "Flame detection for video-based early fire
warning systems and 3D visualization of fire
propagation," in 13th IASTED Int'l Conf. on Computer
Graphics and Imaging.
Dimitropoulos, K., Barboutis, P., Grammalidis, N., 2015.
"Spatio-Temporal Flame Modeling and Dynamic
Texture Analysis for Automatic Video-Based Fire
Detection", IEEE Transactions on Circuits and
Systems for Video Technology, vol. 25, no. 2, pp.
339-351.
Doretto, G., Chiuso, A., Wu, Y. N., Soatto, S., 2003.
"Dynamic Textures," Int'l J. of Computer Vision, vol.
51, no. 2, pp. 91-109.
Fothergill, S., Mentis, H. M., Kohli, P., Nowozin, S.,
2012. Instructing people for training gestural
interactive systems. In J. A. Konstan, E. H. Chi, and
K. Hook, editors, CHI, pages 1737–1746. ACM.
Kaufman, L., Rousseeuw, P.J., 1987. Clustering by means
of Medoids. In Statistical Data Analysis Based on the
L1–Norm and Related Methods, edited by Y. Dodge,
Extracting Dynamics from Multi-dimensional Time-evolving Data using a Bag of Higher-order Linear Dynamical Systems
687

North-Holland, 405–416.
Kuo, C. T., 2013. "Higher order SVD: theory and
algorithms".
McFarlane, N., Schofield, C., 1995. "Segmentation and
tracking of piglets in images," British Machine Vision
and Applications, vol. 8, pp. 187-193.
Ravichandran, A., Chaudhry, R., Vidal, R., 2013.
"Categorizing dynamic textures using a bag of
dynamical systems," IEEE Trans. on Pattern Analysis
and Machine Intelligence, vol. 35, no. 2, pp. 342-353,
February.
Soatto, S., Doretto, G., Wu, Y., 2001. Dynamic Textures.
Intl. Conf. on Computer Vision.
Turaga, P., Veeraraghavan, A., Srivastava A. Chellappa
R., 2011. "Statistical Computations on Grassmann and
Stiefel Manifolds for Image and Video based
Recognition," IEEE Trans. on Pattern Analysis and
Machine Intelligence, November.
Vishwanathan, S., Smola, A., Vidal, R., 2007. "Binet-
Cauchy Kernels on Dynamical Systems and Its
Application to the Analysis of Dynamic Scenes," Int'l
J. Computer Vision, vol. 73, no. 1, pp. 95-119.
Vondrick, C., Khosla, A., Malisiewicz T., Torralba, A.,
2013. "HOGgles: Visualizing Object Detection
Features," in Int'l Conf. on Computer Vision, Sydney,
Australia, December.
RGB-SpectralImaging 2016 - Special Session on RBG and Spectral Imaging for Civil/Survey Engineering, Cultural, Environmental,
Industrial Applications
688
