
The Benefit of Control Knowledge and Heuristics
During Search in Planning
Jind
ˇ
rich Vodr
´
a
ˇ
zka and Roman Bart
´
ak
Charles University in Prague, Faculty of Mathematics and Physics, Malostransk
´
e n
´
am. 25, Prague, Czech Republic
Keywords:
Search, Branch and Bound, Iterative Deepening, Planning, Control Knowledge, Heuristics, Planning Domain.
Abstract:
The overall performance of classical planner depends heavily on the domain model which can be enhanced
by adding control knowledge and heuristics. Both of them are known techniques which can boost the search
process in exchange for some computational overhead needed for their repeated evaluation. Our experiments
show that the gain from usage of heuristics and control knowledge is evolving throughout the search process
and also depends on the type of search algorithm. We demonstrate the idea using the branch-and-bound and
iterative deepening search techniques, both implemented in the Picat planning module.
1 INTRODUCTION
Automated planning is a model-based approach to
problem solving with decades of research history. The
model is usually used to describe some dynamic sys-
tem called a domain. For example we can model a
simple world with trucks that transport packages be-
tween locations. The description lists possible object
types (e.g. trucks, packages, locations), their relations
and properties by means of predicate logic. For in-
stance we can define predicate connected(Loc,Loc)
which describes the fact that two locations are con-
nected by road and predicate in(Pkg,Truck) to de-
scribe that a package is loaded in a truck. The state of
the world in a particular situation is then described as
a set of grounded predicates.
In order to model dynamics of the system we need
to describe possible state transitions. We can do this
by describing so called operators. An operator can be
best understood as a template that can describe many
similar state transitions that differs only in their pa-
rameters. In planning a state transition is called an
action and it consists of four parts. Here is an exam-
ple action drive(t,l1,l2) describing the move of
the truck t from location l1 to location l2:
• the ordered list of parameters: [t,l1,l2]
• the list of preconditions:
[at(t,l1),connected(l1,l2)]
• the list of positive effects: [at(t,l2)]
• the list of negative effects: [at(t,l1)]
An action is applicable in a given state if all the pre-
conditions holds (e.g. the truck t is at the location
l1 and the locations l1 and l2 are connected). A new
state can be obtained from the original state by adding
all the positive effects and removing all the negative
effects of applicable action.
The predicates and the operators together consti-
tutes a planning domain. In order to specify a plan-
ning problem instance we need to define some initial
state and a goal condition. The planning domain with
an instance of the planning problem define a search
space. The solution for the planning problem instance
is a sequence of actions that leads from the initial state
to some state where the goal condition is satisfied.
The approach just described is called classical plan-
ning (Ghallab et al., 2004).
The model used in the classical planning provides
ground for this paper. Since the International Plan-
ning Competitions (IPC’s) the Planning Domain Def-
inition Language (PDDL) (McDermott et al., 1998)
is the most commonly used language for describing
planning domains and problems. The domain models
developed in PDDL for IPC use the “physics only”
modeling principle where the model describes only
how actions change the state of the world but they
do not indicate how the problem should be solved.
The automated planners working with PDDL are then
called domain-independent planners as they do not
expect any domain specific information in the model.
Even for relatively small problem instances the
search space is usually vast due to combinatorial com-
plexity. There are both domain independent and do-
552
Vodrážka, J. and Barták, R.
The Benefit of Control Knowledge and Heuristics During Search in Planning.
DOI: 10.5220/0005828005520559
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 2, pages 552-559
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

main specific techniques designed to prune the search
space and to direct the search algorithm towards the
goal.
Heuristic search proved to be a very strong do-
main independent technique. For example we can re-
fer to the Fast Forward planning system (Hoffmann
and Nebel, 2001) which uses a heuristic estimate
of distance to the goal or the HSP planner (Bonet
and Geffner, 2001) which can automatically extract
heuristic function from the domain model.
It is known that domain specific information im-
proves efficiency of planners significantly (Haslum
and Scholz, 2003). There are planners that use state
centric domain control knowledge specified in tem-
poral logic (Bacchus and Kabanza, 1999), (Kvarn-
str
¨
om and Magnusson, 2003). Action-centric control
knowledge can be encoded in hierarchical task net-
works (Nau et al., 2003) and it is also possible to au-
tomatically recompile similar kind of control knowl-
edge into PDDL (Baier et al., 2007).
In this paper we focus on two basic search tech-
niques – branch and bound, iterative deepening – in
combination with two domain modeling approaches
that add domain specific information (heuristic func-
tion and control knowledge rules). In particular we
investigate the role of heuristics and control knowl-
edge in the process of search for optimal plans. When
compared to previously mentioned work we use sim-
ple action centric control knowledge in the form of
additional preconditions, which is easy to describe,
and admissible heuristic functions, which compute
the lower bound for plan length
1
. We use the heuris-
tic function in a different way than the A
∗
-based algo-
rithms do. Instead of labeling unvisited states in order
to sort them we use the value of the heuristic function
to prune some branches that can never lead to the goal
because the search would run out of resources first.
We would like to demonstrate that contribution of
control knowledge and heuristic function is not con-
stant during search for the optimal plan in the con-
text of a given search technique. We have performed
a series of experiments in order to investigate if we
can exploit this fact. The most straightforward way to
do this could be saving the time spent to compute the
heuristic function by simply not computing the heuris-
tics when it yields only negligible improvement over
model without heuristics. This might also allow us
to use stronger heuristic functions. Such a function
might slow down the search when computed all the
time but it might help to improve performance if com-
puted in the right moment.
1
Working code example for nomystery domain that uses
control knowledge and heuristic function is available at
http://picat-lang.org/projects.html
The structure of this paper is as follows. Firstly
we will give some background on the automated plan-
ning and the Picat programming language that was
used to conduct the experiments. Then we will intro-
duce three planning domains used in the experiments
together with descriptions of the control knowledge
and heuristic function used. In the fourth section we
will describe and evaluate the experiments performed.
Finally we will discuss the results obtained and draw
some conclusions for possible future work.
2 BACKGROUND
2.1 Automated Planning
Classical AI planning deals with finding a sequence
of actions that change the world from some initial
state to a goal state (Ghallab et al., 2004). We can
see AI planning as the task of finding a path in a di-
rected graph, where nodes describe states of the world
and arcs correspond to state transitions via actions.
Let γ(s,a) describe the state after applying action a to
state s, if a is applicable to s (otherwise the function
is undefined). Then the planning task is to find a se-
quence of actions a
1
,a
2
,..., a
n
called a plan such that,
given the initial state s
0
, for each i ∈ {1, ...,n}, a
i
is
applicable to the state s
i−1
, s
i
= γ(s
i−1
,a
i
), and s
n
is
a final state. For solving cost optimization problems,
a non-negative cost is assigned to each action and the
task is to find a plan with the smallest cost. The major
difference from classical path-finding is that the state
spaces for planning problems are extremely huge and
hence a compact representation of states and actions
(and state transitions) is necessary.
2.2 Picat Planning Module
Picat (Zhou, 2015) is a multi-paradigm logic-based
programming language aimed for general purpose ap-
plications. Aside from its other capabilities the lan-
guage features a built-in planner module with sim-
ple interface which was one of the main reasons why
we chose it to perform our experiments.
User only needs to define the initial state which
is normally a ground Picat term and several predi-
cates. In particular the predicate final(S) that is
used to check whether S is the goal state and predicate
action(S,NextS,Action,ACost), that encodes the
state transition diagram of the planning problem. The
state S can be transformed into NextS by performing
Action. The cost of the action is ACost. If the plan
length is the only interest, then ACost can be set to 1.
Otherwise it should be a non-negative number.
The Benefit of Control Knowledge and Heuristics During Search in Planning
553

The general structure for an action rule in Picat is
as follows:
action(S,NextS,Action,ACost),
precondition,
[control_knowledge]
?=>
description_of_next_state,
action_cost_calculation,
[heuristic_and_deadend_verification].
The planner module uses basically two search
approaches to find the optimal plan. Both of them are
based on depth-first search with tabling (Bart
´
ak and
Vodr
´
a
ˇ
zka, 2015) and in some sense they correspond
to classical forward planning. It means that they start
in the initial state, select an action rule that is applica-
ble to the current state, apply the rule to generate the
next state, and continue until they find a state satisfy-
ing the goal condition defined by the predicate final
or fails. In that case the algorithm backtracks and se-
lects another applicable action rule until there are no
alternatives.
The first approach is very close to branch-and-
bound technique (Doig et al., 1960). Note that tabling
is used there – best plans found are remembered for
all visited states and can be reused when visiting the
state next time instead of searching again.
The second approach exploits the idea of itera-
tively extending the plan length (iterative deepening)
as proposed first for SAT-based planners (Kautz and
Selman, 1992). Unlike the IDA* search algorithm
(Korf, 1985), which starts a new round from scratch,
Picat reuses the states that were tabled in previous
rounds.
3 DOMAIN MODELS
For our experiments we have selected three bench-
mark domains. Namely Depots from IPC 2002, No-
mystery from IPC 2011 and Childsnack from IPC
2014. In order to include control knowledge and
heuristics easily we have reformulated the original
PDDL code into Picat programs. Automatic refor-
mulation algorithm for basic domain models without
control knowledge and heuristic is currently under de-
velopment. Therefore we have limited our selection
to domains with small number of actions because we
needed to reformulate them manually.
The reformulation of each domain resulted in a
basic model which was then used as a template for
another three versions. In the first version we added
heuristic function, the second version was enhanced
with simple control knowledge and the last version in-
cludes both heuristic and control knowledge together.
Brief descriptions of the domains follow. The
heuristics and the control knowledge used are de-
scribed in (Bart
´
ak and Vodr
´
a
ˇ
zka, 2016).
3.1 Depots
Depots is a combination of two well known planning
domains: Logistics and Blocksworld. They are com-
bined to form a domain in which trucks can transport
crates around and then the crates must be stacked onto
pallets at their destinations. The stacking is achieved
using hoists, so the stacking problem is like a blocks-
world problem with multiple block manipulators. The
representation used for the experiments mimics the
original PDDL domain model.
3.2 Nomystery
In the Nomystery domain, there is a single truck with
unlimited load capacity, but with a given (limited)
quantity of fuel. The truck moves in a weighted
graph where a set of packages must be transported
between nodes. Actions move the truck along edges
and load/unload packages. Each move consumes the
edge weight in fuel so the initial fuel quantity limits
how far the truck can move (no refueling is assumed).
The goal is to transport all the packages to their desti-
nations using the shortest plan possible.
3.3 Childsnack
The task in this domain is to plan how to make and
serve sandwiches for a group of children in which
some are allergic to gluten. There are two actions for
making sandwiches from their ingredients. The first
one makes a sandwich and the second one makes a
sandwich taking into account that all ingredients are
gluten-free. There are also actions to put a sandwich
on a tray and to serve sandwiches. Problems in this
domain define the ingredients to make sandwiches
at the initial state. Goals consist of having all kids
served with a sandwich to which they are not allergic.
4 EXPERIMENTAL EVALUATION
We have performed a set of experiments using the two
search techniques implemented in the Picat planner
module. Namely we have used the branch and
bound (BB) search and the iterative deepening (ID)
search accessible in predicates best_plan_bb and
best_plan. Each of the two search techniques was
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
554

used to solve three sets of benchmark problems
2
us-
ing the four variants of reformulated domain model
introduced in Section 3.
For each problem instance, the runtime was lim-
ited to 30 minutes and memory to 1GB. We have used
parallel computation for our experiments (Tange,
2011). The experiments run on a computer with In-
telR CoreTM i7-960 at 3.20GHz with 24 GB of RAM
(1066 MHz).
Every run of the planner was monitored in order
to collect data that would describe the progress of
the search algorithm. The collected data was used to
compare performance of given search strategy when
used with different domain models. For example
the data collected when solving a specific problem
instance using BB search in combination with the
model enhanced with heuristic function can be com-
pared to the data collected on the same problem in-
stance using BB search again but with another model
without the heuristic function.
For both search strategies we have measured time
between specific events that occurred during search.
In case of BB search we have recorded the time
elapsed between beginning of the search and each
valid suboptimal plan found. For ID search we have
recorded the time elapsed between incremental steps
of the algorithm i.e. every time when the bound for
the plan length was increased. Note that in this way
the data was collected even if the optimal solution was
not found within the time and memory limits stated
above.
Technical details
The data were collected using standard features
of the Picat programing language. The measure-
ment of time intervals during the BB search was
made possible by modifying the predicate final
in the following way:
final(S) => check(S),record_time().
Where the custom domain dependent predicate
check is used to recognize a final state and
the function record_time() records the current
plan length and time in a text file for further pro-
cessing.
For the ID search we have used a different
method:
final(_) ?=>
if current_plan_length() == 0 then
record_time()
end,fail.
final(S) => check(S).
2
Original PDDL domain models together with problem
instances can be found in publicly available repository at
https://bitbucket.org/planning-tools/domains.
Note that the ?=> symbol defines a backtrack-
able rule. As the first rule always fails Picat
will use it only to record time when the ID al-
gorithm finishes the search for a given bound
and starts again with length zero. The functions
record_time and current_plan_length can
be implemented using standard predicates avail-
able in Picat’s planner and sys modules.
The Table 1 summarizes the number of problem
instances used for the experiment. In the first two
columns we can read the name of the domain and the
total number of benchmark instances used.
The third column is included in order to pro-
vide comparison with state-of-the-art planners. For
each domain we present the number of problem in-
stances solved optimally by best performing plan-
ner participating at the respective IPC where the do-
main was last used. For the depots domain the data
was not available since there was no optimal track in
the competition. Note that there were only 20 prob-
lem instances included for the nomystery domain at
IPC 2011 whereas our set of benchmarks contains 30
problem instances. In the Table 1 we compared to op-
timizing version of the Fast Downward Stone Soup 1
planner (Helmert et al., 2011) in the case of the no-
mystery domain. In the case of the childsnack do-
main we compared to the best performing planner for
the domain in the competition which is the dynamic-
gamer (Kissmann et al., 2014).
In the following four columns, labeled basic, ctrl,
heur and ctrl+heur, we can see how each variant of
the domain model performed when used with either
BB search or ID search strategy. The largest num-
ber of optimally solved benchmarks is emphasized for
each domain.
Table 1: Solved benchmarks.
basic ctrl heur ctrl+heur
Domain #problems SOA bb id bb id bb id bb id
depots 22 N/A 1 2 11 11 1 4 13 13
nomystery 30 20 6 6 27 27 7 28 28 30
childsnack 20 10 0 0 20 20 0 0 20 20
4.1 Branch and Bound
In the initial stage of BB search (i.e. until the discov-
ery of the first valid plan) the bound for the plan length
is set to infinity
3
. Since the heuristic function works
by pruning branches by comparing its value with this
bound there will be hardly any contribution. In con-
trast the control knowledge should prove useful espe-
cially at the very beginning since it helps to direct the
3
In practice we set the initial bound to 9999.
The Benefit of Control Knowledge and Heuristics During Search in Planning
555

search algorithm towards “good” solutions. Based on
this observation we state the following two hypothe-
sis:
Hypothesis 1. The contribution of heuristic function
used in BB search is neglible until the first valid solu-
tion is discovered. The heuristic function contributes
to improve a suboptimal solution and to prove its op-
timality.
Hypothesis 2. The contribution of control knowledge
used in BB search is high in the initial stage. After
the optimal solution was found the control knowledge
does not contribute much to prove its optimality.
In order to evaluate the experiment for the BB
search algorithm we define the following three phases
of the search process. We will refer to the quality of
the current plan found so far:
1. In the phase 1 the quality of the plan is unknown
because there is no plan found yet.
2. In the phase 2 the quality of the plan increases.
3. In the phase 3 the quality of the plan remains un-
changed. In this phase the algorithm only needs
to prove that the plan is the optimal one.
We can observe the three phases in all sample
problems displayed in Figure 1 except for the child-
snack domain. The problem instances were selected
to illustrate the search process for each domain. Note
that the Y axis displays plan quality instead of plan
cost which was actually measured in the experiment.
In order to enable comparison across different prob-
lem instances we have computed plan quality Q from
plan cost C and optimal plan cost
4
C
∗
as Q = C
∗
/C.
We can see the trend stated in the hypothesis 1
demonstrated itself in depots and nomystery domains.
The childsnack domain does not show much informa-
tion since the planner run was too quick. This can be
attributed to the fact that in the childsnack domain the
model is equipped with strong control knowledge.
Table 2 summarizes the results for the BB search
experiments. For each domain the table displays five
rows. In the first row we can find the number of prob-
lem instances solved. The second row lists arithmetic
means of qualities of initial solutions. The third row
shows the total time needed by the algorithm to solve
the problem instances. The three rows labelled t1 -
t3 lists fractions of time spent in the three phases de-
scribed earlier. For each model the values were com-
puted by summing the respective times (e.g. time to
discover the initial solution) for all the problem in-
stances that were solved using the model. Then the
resulting sum was normalized with respect to the total
4
This is a common practice at IPC’s.
time elapsed. The columns are labelled by the models
used.
We were not able to compare all pairs of mod-
els due to big differences in the count of the prob-
lems solved. However we made the following obser-
vations:
1. The overall fraction of time, spent in the phase
1, is lower or equal for the models without the
heuristic function (basic, ctrl) than for the corre-
sponding models with the heuristic function (heur,
ctrl+heur). In fact the value is even increased in
the nomystery domain.
2. The overall fraction of time, spent in the phase 2
and 3, is usually lower for the models with heuris-
tic function (heur) compared to the basic models
(basic). The decrease can be best observed in the
nomystery domain. The data for the depots do-
main are insufficient for analysis and in the child-
snack domain there are no data at all.
3. The overall fraction of time, spent in the phase 2
and 3, is lower for the models with control knowl-
edge and heuristic function (ctrl+heur) compared
to the models with control knowledge only (ctrl).
The only exception is for the phase 2 in the child-
snack domain. There is only decent decrease in
the depots domain but the fraction is significantly
lowered in the case of nomystery domain.
4. We can see that the first solution found is already
quite good for the models that use control knowl-
edge (ctrl, ctrl+heur). In fact when using the mod-
els without control knowledge (basic,heur) the
search algorithm rarely managed to find a valid
solution within the time and memory limits. This
trend can be observed in all domains.
5. The count of solved problem instances is signif-
icantly lower for models without control knowl-
edge than for corresponding models with control
knowledge included.
All the observations are in accordance with the hy-
pothesis 1 and 2. The exceptions observed can be
attributed to the short runtime of easy problem in-
stances.
4.2 Iterative Deepening
In contrast with the BB search the bound for the plan
length in the ID search is tight from the very begin-
ning of the search. Therefore we expect the heuristic
function to prune many branches and contribute a lot
in the early stage (i.e. when the difference between
the bound and the length of the optimal plan is big).
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
556

Table 2: Branch and bound summary.
domain basic ctrl heur ctrl+heur
depots
#problems 1 11 1 13
init. quality mean 0.009 0.932 0.005 0.932
total time (s) 1.7 1730.0 1.9 1534.6
t1 0.86 0.00 0.86 0.00
t2 99.14 4.16 99.09 3.43
t3 0.00 95.84 0.05 96.57
nomystery
#problems 6 27 7 28
init. quality mean 0.668 0.873 0.671 0.873
total time (s) 150.4 813.9 1085.4 2673.1
t1 72.07 48.64 85.52 94.92
t2 16.59 32.17 14.47 4.95
t3 11.34 19.19 0.01 0.13
childsnack
#problems 0 20 0 20
init. quality mean - 0.974 - 0.974
total time (s) - 0.6 - 0.01
t1 - 1.12 - 71.43
t2 - 5.77 - 7.14
t3 - 93.11 - 21.43
Figure 1: Evolution of plan quality in time during branch
and bound search for selected problem instances from each
domain.
On the other hand we do not expect the control knowl-
edge to help much in the early stage since the algo-
rithm needs to check all the branches anyway. The
guidance provided by the control knowledge rules is
not needed until the gap between the bound and the
length of the optimal plan decreases. We have stated
the following pair of hypothesis concerning the con-
tribution of heuristic functions and control knowledge
in the context of ID search:
Hypothesis 3. The heuristic function contributes sig-
nificantly to reduce the time for iteration of the ID
search algorithm in the early stage. This effect di-
minishes as the bound increases towards the length of
the optimal plan.
Hypothesis 4. The control knowledge is not essen-
tial for the ID search when there is a big gap between
the optimal plan length and the plan bound used by
the algorithm. When the bound is close to the opti-
mal plan length the control knowledge helps to reduce
time by guiding the search algorithm towards the op-
timal solution.
Unlike the BB search, which needs to prove the
optimality of the solution after it is discovered, the ID
search algorithm maintains the ”proof” of optimality
from the very beginning. In the data samples visual-
ized in Figure 2, we can see how much time (the axis
X) the algorithm needed to prove the fact that the opti-
mal plan is longer than some bound (the axis Y). Note
that not all models reach the bound set by the length
of the optimal solution (e.g. basic model with control
knowledge in the depots domain). This is due to the
time and memory limits.
Since there is no obvious way how to distinguish
different phases of the search process for the ID al-
gorithm we were not able to summarize the results in
similar way as in the case of the BB search. There-
fore we list only the number of the problems solved
optimally, together with the total time needed to solve
them, in Table 3.
Table 3: Iterative deepening summary.
domain basic ctrl heur ctrl+heur
depots
#problems 2 11 4 13
total time (s) 4.54 2062.80 1075.79 1767.42
nomystery
#problems 6 27 28 30
total time (s) 97.37 1980.58 4005.51 100.63
childsnack
#problems 0 20 0 20
total time (s) - 0.99 - 0.03
The selected samples (Figure 2) represent the gen-
eral trends observed in each domain:
1. The model with heuristic function (basic+heur)
usually performs better than the model with con-
trol knowledge (basic+ctrl) when the plan bound
is low. This behavior tends to change with in-
creasing bound. The childsnack domain domain
is the only exception to this trend. This might be
The Benefit of Control Knowledge and Heuristics During Search in Planning
557
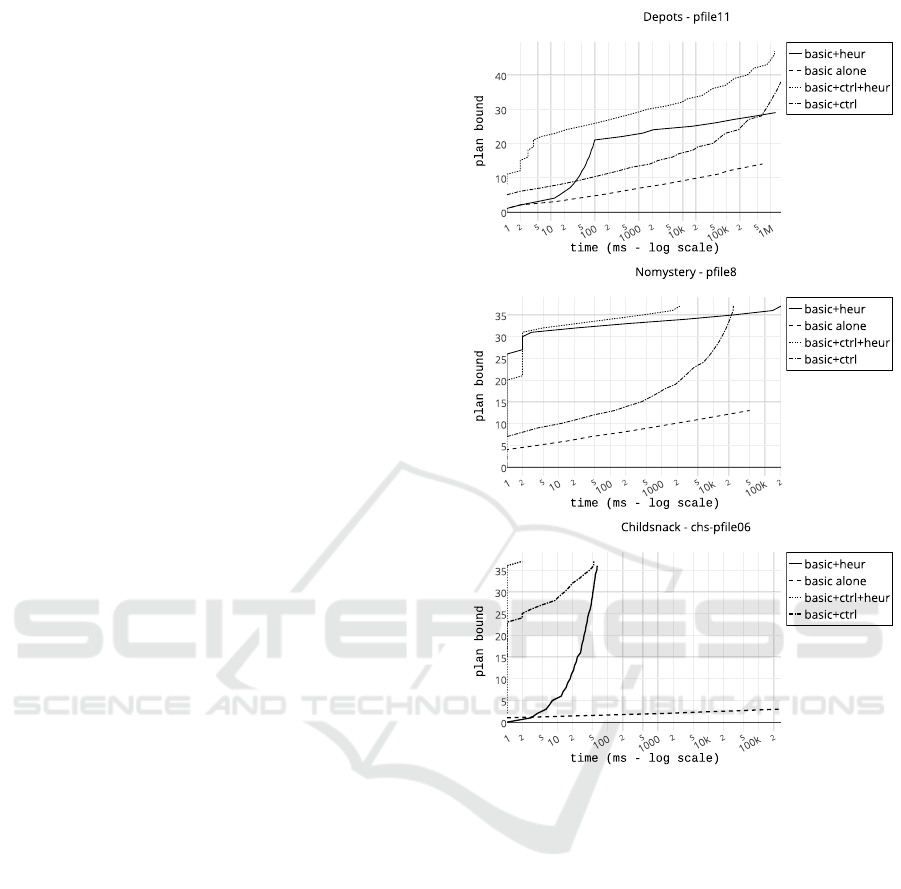
caused by the fact that the heuristic function used
in the childsnack domain is much more expensive
to compute than the control knowledge.
2. The model enhanced with heuristic and control
rules performed better than the model with heuris-
tic only. In most of the samples we were able
to identify similar situation as in the depots sam-
ple where the more complex model with control
knowledge starts to gain advantage over the sim-
pler model when the plan bound 21 is reached.
3. The model enhanced with control knowledge and
heuristic (basic+ctrl+heur) function performed
better than the model with control knowledge only
(basic+ctrl). The majority of the samples dis-
plays trend similar to the situation in the nomys-
tery sample where the more complex model starts
to lose its advantage around the bound 30.
All the observations are in accordance with the hy-
pothesis 3 and 4. In case of the childsnack domain
where we have observed some unexpected behavior
we have to consider the fact that all the benchmarks
were solved in fraction of one second (see Table 3).
5 CONCLUSIONS
We have used two different search strategies, namely
the branch and bound and the iterative deepening
implemented in the planning module of the Picat
programming language, to solve several benchmark
problems in three different planning domains. In or-
der to examine the contribution of two modeling tech-
niques, namely control knowledge and heuristic func-
tions, we have created four variants of the domain
models reformulated from PDDL into Picat.
Although the experiments were realized using the
Picat programming language, the results should be
valid in general for the two search strategies consid-
ered. Any planner based on similar principles can
benefit from our analysis.
We have formulated two hypothesis for both
search strategies that describe how the heuristics and
control knowledge are used during the search. The
control knowledge “guide” the algorithm towards the
optimal plan and does not help much to prove its op-
timality. On the other hand the heuristics can be used
to prove that there is no “short” plan and do not help
much to find the plan.
According to the hypothesis 1 and 2 it should be
possible to save time in BB search by finding first so-
lution with control knowledge alone and then use the
heuristic function to improve it. Another approach
for the ID search is indicated by the hypothesis 3 and
Figure 2: The time spent to prove that there is no plan
shorter than a given bound. Plots for selected problem in-
stances from each domain.
4. In principle we should be able to swap heuristic
function for control knowledge rules in some point
of the search process and save some time here too.
Such mechanism could also enable usage of stronger
heuristic functions or control rules that would be oth-
erwise too expensive for computation.
The data obtained from the experiments are in ac-
cordance with our initial intuition stated in the hy-
pothesis. In particular we have identified several
problem instances that indicate that it should be possi-
ble to save CPU time by completely disabling heuris-
tic function or partially deactivating control knowl-
edge when not needed. The timing of such operation
depends on the problem instance size and quality of
both heuristic function and control knowledge. The
differences in quality are reflected in figures 1 and 2.
The method for timing and quality estimation are pos-
sible subjects of further research.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
558

The models used in the experiments use hand-
coded heuristics and control knowledge. The method
how to extract the control knowledge automatically
from the domain description is subject of further re-
search.
ACKNOWLEDGEMENTS
Research is supported by the Czech Science Foun-
dation under the project P103-15-19877S and by the
Grant Agency of Charles University under the project
No. 241515.
REFERENCES
Bacchus, F. and Kabanza, F. (1999). Using temporal log-
ics to express search control knowledge for planning.
Artificial Intelligence, 116:2000.
Baier, J., Fritz, C., and McIlraith, S. A. (2007). Exploiting
procedural domain control knowledge in state-of-the-
art planners. In Proceedings of the 17th International
Conference on Automated Planning and Scheduling
(ICAPS), pages 26–33.
Bart
´
ak, R. and Vodr
´
a
ˇ
zka, J. (2015). Searching for sequential
plans using tabled logic programming. In 22nd RCRA
International Workshop on Experimental Evaluation
of Algorithms for solving problems with combinatorial
explosion.
Bart
´
ak, R. and Vodr
´
a
ˇ
zka, J. (2016). The effect of domain
modeling on the performance of planning algorithms.
In International Symposium on Artificial Intelligence
and Mathematics (ISAIM).
Bonet, B. and Geffner, H. (2001). Planning as heuristic
search. Artificial Intelligence, 129:5–33.
Doig, A. G., Land, B. H., and Doig, A. G. (1960). An auto-
matic method for solving discrete programming prob-
lems. Econometrica, pages 497–520.
Ghallab, M., Nau, D., and Traverso, P. (2004). Automated
Planning: Theory & Practice. Morgan Kaufmann
Publishers Inc., San Francisco, CA, USA.
Haslum, P. and Scholz, U. (2003). Domain knowledge in
planning: Representation and use. In Proc. ICAPS
2003 Workshop on PDDL.
Helmert, M., Rger, G., Seipp, J., Karpas, E., Hoffmann,
J., Keyder, E., Nissim, R., Richter, S., and Westphal,
M. (2011). Fast downward stone soup. Available at:
http://www.fast-downward.org/IpcPlanners.
Hoffmann, J. and Nebel, B. (2001). The ff planning system:
Fast plan generation through heuristic search. Journal
of Artificial Intelligence Research, 14(1):253–302.
Kautz, H. and Selman, B. (1992). Planning as satisfiability.
In ECAI-92, pages 359–363. Wiley.
Kissmann, P., Edelkamp, S., and Hoffmann, J. (2014).
Gamer and dynamic-gamer symbolic search
at ipc 2014. Available at: https://fai.cs.uni-
saarland.de/kissmann/planning/downloads/.
Korf, R. E. (1985). Depth-first iterative-deepening: An op-
timal admissible tree search. Artificial Intelligence,
27:97–109.
Kvarnstr
¨
om, J. and Magnusson, M. (2003). Talplanner in
the third international planning competition: Exten-
sions and control rules. Journal of Artificial Intelli-
gence Research, 20:343–377.
McDermott, D., Ghallab, M., Howe, A., Knoblock, C.,
Ram, A., Veloso, M., Weld, D., and Wilkins, D.
(1998). PDDL - the planning domain definition lan-
guage. Technical report, CVC TR-98-003/DCS TR-
1165, Yale Center for Computational Vision and Con-
trol.
Nau, D., Ilghami, O., Kuter, U., Murdock, J. W., Wu,
D., and Yaman, F. (2003). Shop2: An htn planning
system. Journal of Artificial Intelligence Research,
20:379–404.
Tange, O. (2011). Gnu parallel - the command-line power
tool. ;login: The USENIX Magazine, 36(1):42–47.
Zhou, N. F. (2015). Picat web site. http://picat-lang.org/.
Accessed October 18.
The Benefit of Control Knowledge and Heuristics During Search in Planning
559
