
Actuation-based Shape Representation Applied to
Engineering Document Analysis
Thomas C. Henderson, Narong Boonsiribunsum and Anshul Joshi
School of Computing, University of Utah, Salt Lake City, UT, U.S.A.
Keywords:
Shape Analysis, Cognitive Representations, Agents, Document Analysis.
Abstract:
We propose that human generated drawings (including text and graphics) can be represented in terms of
actuation processes required to produce them in addition to the visual or geometric properties. The basic
theoretical tool is the wreath product introduced by Leyton (Leyton, 2001) (a special form of the semi-direct
product from group theory which expresses the action of a control group on a fiber group) which can be
used to describe the basic strokes used to form characters and other elements of the drawing. This captures
both the geometry (points in the plane) of a shape as well as a generative model (actuation sequences on
a kinematic structure). We show that this representation offers several advantages with respect to robust and
effective semantic analysis of CAD drawings in terms of classification rates. Document analysis methods have
been studied for several decades and much progress has been made; see (Henderson, 2014) for an overview.
However, there are many classes of document images which still pose serious problems for effective semantic
analysis. Of particular interest here are CAD drawings, and more specifically sets of scanned drawings for
which either the electronic CAD no longer exists, or which were produced by hand. We demonstrate results
on a set of CAD-generated drawings for automotive parts.
1 INTRODUCTION
Our main result here is the development of a novel
shape analysis method and the demonstration of its
effectiveness in the text analysis of engineering CAD
documents. Figure 1 shows the overall scheme for
both 2D and 3D datasets.
The 2D data of interest here consists of scanned
engineering drawings like those shown in Figure 2.
The image analysis consists of the extraction of basic
shape symmetries (represented as wreath products),
followedby symmetry parsing (givenas Wreath Prod-
uct Constraint Sets), finally passing through a classi-
Figure 1: Overall Symmetry Analysis Flow.
fication component where hypotheses are formed as
described in the figure. We provide a formal gram-
mar for this parsing in which the lowest level termi-
nal symbols are simple symmetries and nonterminal
symbols correspond to more complex shapes. The
hypotheses produced by the system are ranked ac-
cording to a Bayesian analysis based on the wreath
product directed acyclic graph as well as the parse
tree. Much work has been done in engineering docu-
ment analysis (see (Henderson, 2014) for a detailed
survey), but to our knowledge, there are few im-
plemented systems in which shape is represented in
terms of actuation primitives. One example of such
work is that of Plamondon (Plamondon, 1995a; Pla-
mondon, 1995b; Plamondon, 1998; Plamondon et al.,
2014)), but that approach has a very different ba-
sis rooted in the kinematics of human rapid move-
ment. Other recent studies of more global properties
of document analysis, e.g., using deep convolutional
networks (Harley et al., 2015; Kang et al., 2014),
are more conventional in that they are still based on
the geometric properties of the points comprising the
shape, rather than exploiting how the shape is synthe-
sized. For another survey of document analysis and
recognition, see (Marinai, 2008).
500
Henderson, T., Boonsiribunsum, N. and Joshi, A.
Actuation-based Shape Representation Applied to Engineering Document Analysis.
DOI: 10.5220/0005818805000505
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 2, pages 500-505
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Leyton (Leyton, 2001) introduced a generative
theory of shape, and his key insight was that the set
of points in a shape may be generated in many dif-
ferent ways, and that these ways can be characterized
technically by a wreath product group. We propose
that such a sensorimotor representation is more suit-
able for an embodied agent than a purely geometric
or static feature method. The wreath product com-
bines two levels of description: (1) a symbolic one
based on group action sequences (i.e., strings), and
(2) shape synthesis based on group actions on other
groups (i.e., motion descriptions). For example, a line
segment may be generated by moving a point along a
line for a certain distance – represented by the wreath
product: e ≀ Z
2
≀ ℜ; however, in order to realize this
for a specific line segment, an actuation mechanism
in the coordinate frame of the shape must be defined
and and actuation commands provided whose appli-
cation results in the kinematic synthesis of the points
in the line segment. For example, eye motion con-
trol to move the fovea along a shape is such a system.
The human arm and its motor control is another. The
abstract form of the wreath product allows either of
these control systems (eye or arm) to generate a line
segment. Thus, shape is a sensorimotor representa-
tion, and one which supports knowledge transfer be-
tween motor systems with known mappings between
them bound together through the abstraction of the
wreath product. Thus, if you see a square with your
eyes, you build a representation which allows the cre-
ation of that shape with your finger, say tracing it in
the sand.
Henderson et al. (Joshi et al., 2014) proposed to
directly incorporate and exploit actuation data in the
analysis of shape. A philosophical and psychological
rˆole for actuation in perception has been given by No¨e
(No¨e, 2004)
The sensorimotor dependencies that gov-
ern the seeing of a cube certainly differ from
those that govern the touching of one, that
is, the ways cube appearances change as a
function of movement is decidedly different
for these two modalities. At an appropriate
level of abstraction, however, these sensori-
motor dependencies are isomorphic to each
other, and it is this fact – rather than any fact
about the quality of sensations, or their corre-
lation – that explains how sight and touch can
share a common spatial content. When you
learn to represent spatial properties in touch,
you come to learn the transmodal sensorimo-
tor profiles of those spatial properties. Percep-
tual experience acquires spatial content thanks
to the establishment of links between move-
Figure 2: Two CAD Drawings; left: text image that is
included with CAD to explain how to paint the structure;
right: a hand-drawn design of a nuclear storage facility.
ment and sensory stimulation. At an appro-
priate level of abstraction, these are the same
across the modalities.
For the basic description of the original work on
the wreath product sensorimotor approach, see (Hen-
derson et al., 2015). Here we go beyond their results
by developing a coherent approach to the semantic
analysis of large sets of CAD drawing images. Fig-
ure 2 shows examples of the types of images we ana-
lyze; on the left is a text file that accompanies an engi-
neering drawing to explain how to paint the structure;
on the right is a hand-drawn design of a nuclear waste
storage facility.
The left image is a text drawing that provides in-
formation about the drawing and the image on the
right is a hand drawn plan for one of the double-
shell nuclear waste storage tanks at Hanford, WA.
The semantic information in such drawings is needed
to develop electronic CAD for automotive parts and
for non-destructive examinations, respectively. The
overall goal is to find the basic character strokes
(defined as Wreath Product Primitives), followed by
character classification (using Wreath Product Con-
straint Sets) and finally word recognition (by dictio-
nary lookup) from those. Figure 3 shows the En-
hanced Non-Deterministic Analysis System (NDAS)
which achieves this analysis; ENDAS uses agents to
achieve a parse of the image. The levels of NDAS
correspond to pre-processing, terminal symbol hy-
potheses, and nonterminal symbol hypotheses. Every
start symbol represents a complete parse of the image
(e.g., a Text Image).
2 THE ENDAS SYSTEM
Leyton proposed a generative model of shape (Ley-
ton, 2001) based on the wreath product group. (Also
see (Viana, 2008; Weyl, 1952) for a discussion of the
Actuation-based Shape Representation Applied to Engineering Document Analysis
501

Figure 3: The ENDAS System.
key issue of invariance as a way to detect regularities
in geometric objects.) The wreath product of F with
C denoted F ≀ C, is defined as the semi-direct prod-
uct of two groups, F and C, where C is the control
(permutation) group which acts on F the fiber group.
More formally:
F ≀C ≡ (
n
∏
i=1
F) ⋊ C
where ⋊ is the semi-direct product (the semi-direct
product is explained in the next section) of n copies
of F with C. C is generally a permutation group with
the permutations applied to the copies of F. The key
notion is that C is the control group that acts to trans-
form the fiber group elements onto each other.
We apply this idea directly to low-level image
analysis of drawings. Some examples of the types of
symmetry include:
• the translation symmetry group denoted by ℜ
(1D): the invariance of pixel sets under transla-
tion defines a straight line segment.
• the rotation symmetry group denoted by O(2)
(2D): the invariance of pixel sets under rotation
defines a circle.
• the reflection symmetry group denoted by Z
2
(2D): the invariance of a set of pixels under re-
flection about a line in the plane describes bilat-
eral symmetry in 2D.
From these symmetry features, we apply this idea
to generate the Wreath Product Constraint Set
(WPCS) to improve the segmentation of low-level ge-
ometric primitives in engineering drawings. For ex-
ample, the lowercase letter set ( ’b’, ’d’, ’p’, ’q’ )
all look similar in shape. But using symmetry analy-
sis, each character shows that the important symmetry
structure in their shape is only one circle (O(2)) and
one straight line (ℜ).
So, we can write a WPCS for each letter ( ’b’, ’d’,
’p’, ’q’ ) to organize the detection of their features
(O(2) and ℜ) in the desired position and differentiate
between these four characters. We then create
agents to search for such WPCS’s.
2.1 Structural Model
In this section we introduce a structural model of tech-
nical drawings that allows an agent-based organiza-
tion of the ENDAS system. We define the layout of
the technical drawings in terms of structural grammar.
G = (V, Σ, R, S) where V is a set of non-terminals, Σ
is a set of terminals, R is a set of rewrite rules, and S
is the start symbol.
2.1.1 Terminal Structure Set
• a|b|...|z|A|B|...|Z|0|1|...|9|%|$|...|#|.|, | −
|
′
|(|)|...|?
• Space ≡ ” ” (image segment which is a white
space)
• HSpace ≡ Space with a nearby left and right seg-
ment
• VSpace ≡ Space with a nearby up and down seg-
ment
• Line ≡ image segment which is a straight solid
line.
• Arc ≡ image segment which is an arc.
• Circle ≡ image segment which is a circle.
2.1.2 Nonterminal Structure Set
• Letter := a|b|...|z|A|B|...|Z
• Digit := 0|1|...|9
• SpecialChar := %|$|...|#
• Punctuation := .|, | − |
′
|(|)|...|?
• Char := Letter | Digit | SpecialChar |
Punctuation
• Word := Char | Char Word
• LineOfText := Word HSpace Word | Word
HSpace LineOfText
• PageOfText := LineOfText VSpace LineOf Text
| LineOfText VSpace PageOfText
• Text := Word | LineO fText | PageOfText
• ArrowHead : Line+ Line
|Line+ Line+ Line
• PointerRay := Line+ ArrowHead
• PointerLine := ArrowHead + Line+ ArrowHead
• PointerArcRay := Arc+ ArrowHead
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
502

• PointerArcLine := ArrowHead + Arc +
ArrowHead
• Box := Line+ Line+ Line+ Line
• PointerPair := (PointerRay +
PointerRay)|(PointerLine+ PointerLine)
• PointerArcPair := (PointerArcRay +
PointerArcRay)|(PointerArcLine +
PointerArcLine)
• Dimension := (PointerPair|PointerArcPair) +
Text
• Graphic := Line|Box|Circle|ArrowHead
|PointerRay|PointerLine|PointerArcRay
|PointerArcLine|Dimension
• TextinBox := Text + Box
• Table := TextinBox TextinBox | TextinBox Table
• GraphicDrawing := Graphic | Graphic Table |
Graphic Text
• TextDrawing := PageOfText | PageOf Text Text
| Table | Table Text
• Drawing := TextDrawing|GraphicDrawing
2.2 Wreath Product
Define a wreath product primitive (WPP) as either a
e ≀ Z
2
≀ ℜ group or a e ≀ Z
2
≀ O(2) group. As a first
step, a set of WPP’s is fit to the pixels in each con-
nected component. Given a connected component
and a WPP set for that component, a minimal WPP
cover set is a combination of WPP’s that cover the
connected component skeleton, and if any WPP is re-
moved, the componentis no longer covered. A wreath
product constraint set (WPCS) is a set of WPPs as
well as any higher level symmetries (e.g., reflection
symmetries which are described in this same coordi-
nate frame as the WPPs).
From each WPP set, the complete set of minimal
WPP cover sets is found, and they provide the initial
characterization of what defines a particular shape.
For example, Figure 4 shows some examples of WPP
minimal cover sets.
Leyton described wreath products abstractly as
symbol sequences and every e≀Z
2
≀ ℜ wreath product
is equivalent to every other. We, however, are faced
with unique, existing instances, and thus, associate a
coordinate frame (generally, the rectangle containing
the symbol) with each as well as descriptions of the
Z
2
mod group which is used to produce finite length
sets (i.e., end points for line segments and angular
limits for circles).
The WPP minimal cover sets shown in Figure 4
are then used to produce a WPCS which will char-
acterize the shape. The additional information in the
0 10 20
0
5
10
15
20
-10 0 10 20
0
5
10
15
20
-10 0 10 20 30
0
10
20
-10 0 10 20 30
0
10
20
-10 0 10 20
0
5
10
15
20
-10 0 10 20 30
0
5
10
15
20
25
Figure 4: Example WPP Minimal Cover Sets.
WPCS over the minimal cover set includes any sym-
metries between WPP’s in the set. For example, the
two WPP’s in the lowercase letters ’a’ and ’e’ have
both vertical and horizontal reflection symmetries; the
letter ’A’ has a vertical reflection symmetry between
the two side arms; the letter ’M’ has vertical reflection
symmetries on the two side arms and the two inner
arms; the digits ’0’ and ’2’ do not have higher level
symmetries.
We have developed a WPCS representation which
is simply a list of the R WPP’s, followed by the O2
WPP’s, and then followed by the higher level wreath
product symmetries found in the shape. For example,
the WPCS’s for the shapes in Figure 4 are character-
ized as:
• ’a’: ’O;O;Z2O;’
• ’A’: ’R;R;R;Z2R’
• ’O’: ’O;Z2O’
• ’e’: ’O;O;Z2O;’
• ’M’: ’R;R;R;R;Z2R;Z2R;Z2R;’
• ’2’: ’R;O;’
The next step in the process is to associate a spe-
cific generative mechanism with the shape. Here we
use the virtual sensors (pan-tilt camera) and actuators
which were proposed in (Henderson et al., 2015); the
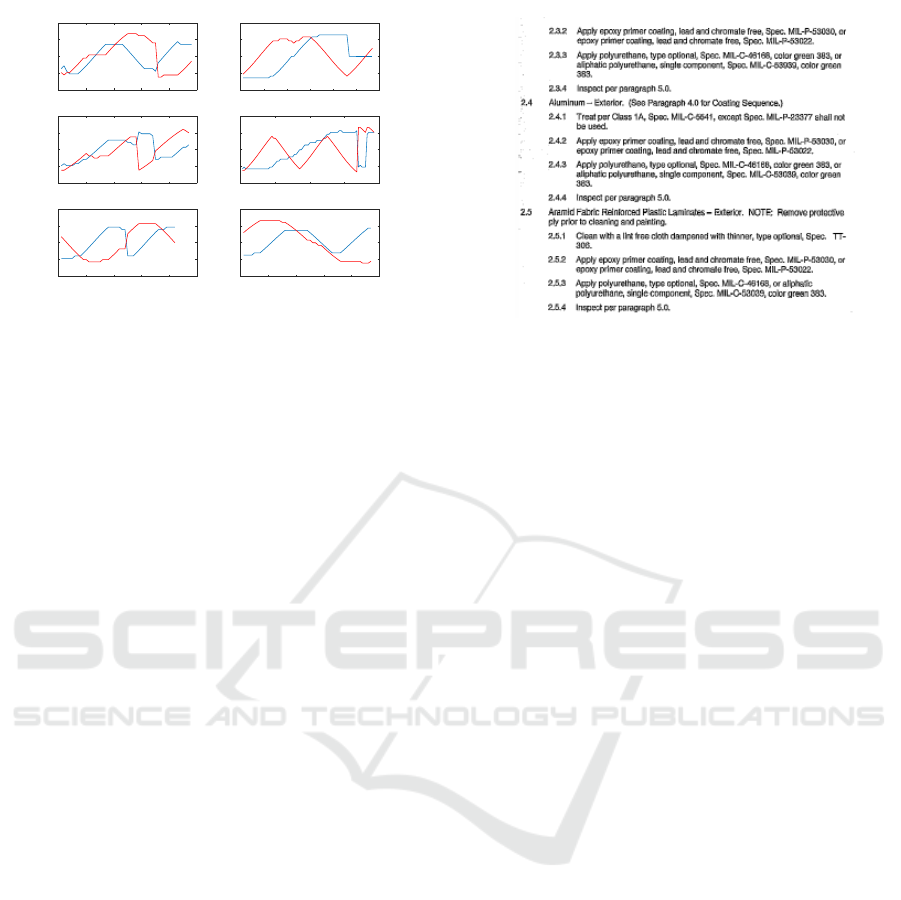
pan-tilt control angles for a camera trace for each of
the characters are shown in Figure 5.
Character classification for an unknown shape is
started by producing the WPCS’s for the shape (note
there may be several). Next, these are compared at
the abstract level to the character template WPCS’s,
and where a match is found, then the pan-tilt actua-
tion generative data are compared. Any match at this
level that is above threshold produces a character hy-
pothesis. The final step uses the character hypotheses
to produce legal word hypotheses(using a dictionary).
Actuation-based Shape Representation Applied to Engineering Document Analysis
503
0 10 20 30 40 50
-1
-0.5
0
0.5
1
0 10 20 30 40 50 60
-1
-0.5
0
0.5
1
0 10 20 30 40 50
-1
-0.5
0
0.5
1
0 20 40 60 80
-1
-0.5
0
0.5
1
0 10 20 30 40 50
-1
-0.5
0
0.5
1
0 10 20 30 40 50
-1
-0.5
0
0.5
1
Figure 5: Pan Tilt Control Angles for the Characters in Fig-
ure 4.
3 EXPERIMENTS
The tests were run of the image shown in Figure 6
which resulted in 1,111 connected components to
classify. The 62 templates for lower and uppercase
letters and the ten digits resulted in 184 minimal cover
WPCS’s for the 62 characters. A total of 3,333 mini-
mal cover WPCS’s were generated for the 1,111 con-
nected components. The abstract wreath product filter
eliminated 67% of the unknown hypotheses; note that
this check only requires comparison of their wreath
product string representations.
The remaining hypotheses were matched to tem-
plates by a 2D pointwise comparison of their pan-tilt
function values. An unknown is considered a match
if the correct character is in the top 5 best pan-tilt dis-
tance matches. The classification rate is very good
with this approach (∼ 99%) when using the top five
hypotheses.
4 CONCLUSIONS AND FUTURE
WORK
We have demonstrated that actuation-based shape
representations using the wreath product groups pro-
vide an effective tool for shape analysis, and in partic-
ular, for engineering drawing analysis. Our position is
that this method works well for text analysis and can
be extended to graphics and handwriting analysis.
In future work, we will:
• study the analysis of the graphics part of the CAD
drawing,
• study the performancein the face of occlusion and
heavy noise,
• apply the method to handwriting recognition and
synthesis, and
Figure 6: Test Image.
• extend the method to 3D and apply it to the as-
built versus as-designed problem.
REFERENCES
Harley, A., Ufkes, A., and Derpanis, K. G. (2015). Evalu-
ation of Deep Convolutional Nets for Document Im-
age Classification and Retrieval. In International Con-
ference on Document Analysis and Recognition (IC-
DAR), Nancy, France.
Henderson, T. (2014). Analysis of Engineering Drawings
and Raster Map Images. Springer Verlag, New York,
NY.
Henderson, T. C., Boonsirisumpun, N., and Joshi, A.
(2015). Actuation in Perception: Character Classifica-
tion in Engineering Drawings. In Proceedings IEEE
Conference on Multisensor Fusion and Integration for
Intelligent Systems, San Diego. IEEE.
Joshi, A., Henderson, T., and Wang, W. (2014). Robot Cog-
nition using Bayesian Symmetry Networks. In Pro-
ceedings of the Internaitonal Conference on Agents
and Artificial Intelligence, Angers, France. IEEE.
Kang, L., Ye, P., Li, Y., and D.Doermann (2014). A Deep
Learning Approach to Document Image Quality As-
sessment. In Proceedings of the IEEE International
Conference on Image Processing, pages 2570–2574,
Paris, France. IEEE.
Leyton, M. (2001). A Generative Theory of Shape.
Springer, Berlin.
Marinai, S. (2008). Introduction to Document Analysis
and Recognition. In Studies in Computational Intel-
ligence, pages 1–20, Berlin, Germany. Springer.
No¨e, A. (2004). Action in Perception. MIT Press, Cam-
brideg, MA.
Plamondon, R. (1995a). A Kinematic Theory of Rapid
Human Movements. I: Movement Representation and
Generation. Bio. Cybernetics, 72(4):295–307.
Plamondon, R. (1995b). A Kinematic Theory of Rapid
Human Movements. II: Movement Time and Control.
Bio. Cybernetics, 72(4):309–320.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
504

Plamondon, R. (1998). A Kinematic Theory of Rapid Hu-
man Movements. III: Kinematic Outcomes. Bio. Cy-
bernetics, 78(2):133–145.
Plamondon, R., O’Reilly, C., Galbslly, J., Almaksour,
A., and Anquetil, E. (2014). Recent Developments
in the Study of Rapid Human Movements with the
Kinematic Theory: Applications to Handwriting and
Signature Synthesis. Pattern Recognition Letters,
35(1):225–235.
Viana, M. (2008). Symmetry Studies. Cambridge University
Press, Cambridge, UK.
Weyl, H. (1952). Symmetry. Princeton University Press,
Princeton, NJ.
Actuation-based Shape Representation Applied to Engineering Document Analysis
505
