Visualising Formula Structures to Support Exploratory Modelling
Chris Roast, Roxanne Leitão and Michael Gunning
Culture, Communication and Computing Research Institute, Sheffield Hallam University,
Sheffield, SW1 1WB, U.K.
Keywords: Spreadsheets, Visualisation, Science Technology Engineering and Maths (STEM).
Abstract: Visualisation is often presented as a means of simplifying information and helping people understand
complex data. In this paper we describe a project designing interactive visualisations to support learner
competencies in the broad area of numeracy. The work builds upon: (i) the observation that while
spreadsheets are traditional ICT tools, their familiarity means that they are used for exploratory
mathematical modelling; (ii) a research theme examining the human factors that influence the ease with
which formal notations can be understood and applied appropriately. Our paper describes the iterative
design and evaluation of a tool to visualise spreadsheets, with the aim of supporting mid-teen learners based
on the premise that spreadsheets serve as a gateway tool for supporting learner experimentation and
confidence within numerate subjects. This iterative process is informed by background research into
notational design, graphic design as well as learner and tutor feedback.
1 INTRODUCTION
Visualisation is often presented as a means of
simplifying information and helping people
understand complex data. In this paper we describe a
project designing interactive visualisations to
support core learner competencies in the broad area
of numeracy. Our premise is that, spreadsheets are a
traditional, common and accessible ICT tool that
supports learner confidence and experimentation of
mathematical modelling. We describe the iterative
design and evaluation of a tool to visualise
spreadsheets, with an aim of supporting mid-teen
learners in work-based education and/or prior to
entering higher education. This process combines
research, graphic design and learner and tutor
feedback to develop a spreadsheet 'plug-in'.
2 BACKGROUND
2.1 Why Spreadsheets?
The relevance of numeracy as a foundation for
educational, academic and professional skills is
widely recognised. This is evidenced by the value
placed on the development of numeracy skills within
science, technology, engineering and maths (STEM)
education. In the UK there are various programmes
to develop maths skills and skills for employment in
engineering and IT. One common accessible tool for
powerful numeric computations is the spreadsheet.
Widely used in work and education (Chambers and
Scaffidi 2010), at school level and in higher
education, the spreadsheet is a core generic tool for
understanding in many numerate subjects. From an
employment and employability perspective, the
spreadsheet is a widely used tool in most businesses.
Despite the spreadsheet being a familiar tool for
general purpose computation, with significant
longevity, Panko (2008) and Hendry and Green
(1993) argue that up to 44% of them contain errors.
In addition, they are not being used to their full
potential - for example 95% of IT related skills gaps
in England being spreadsheet skills (Technology
Insights 2012, e-skills UK).
Research into addressing issues of spreadsheet
quality has motivated many enhancements. This
includes additional features to ensure they are more
transparent as well as to encourage more discipline
in their use. (Burnett et al. Burnett 2002, Hendry and
Green 1994, Hermans and Dig 2014, Panko and
Sprague 1998, Sajaniemi 2000).
We propose that this desire to enhance
spreadsheets arises from their initial ease of use and
Roast, C., Leitão, R. and Gunning, M.
Visualising Formula Structures to Support Exploratory Modelling.
In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016) - Volume 1, pages 383-390
ISBN: 978-989-758-179-3
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
383

responsiveness being in natural opposition to their
subsequent poor information infra-structure that
does not support self-documentation and
modifications. Their responsiveness means their
users quickly become embedded in 'solutions' that
are subsequently hard to manage. Specifically with
regard to the complexity of inter-cell referencing,
the understanding of formulae has been found to be
particularly demanding, with evidence that business
and governmental spreadsheets tend to avoid the use
of many functions and function nesting (Sajaniemi
and Pekkanen 1988). Research into complex
interactive systems and user empowerment
(Blackwell, et al. 2001) has provided a range of
descriptive dimensions that capture some of these
core characteristics. The notion of 'premature
commitment' describes systems that introduce
constraints before users know how to work with
them, or if they want to work with them. Hence, for
traditional spreadsheets simple numeric models are
easy but well-structured models benefit from
planning up-front. Complementing this is the notion
of 'viscosity' (a resistance to change). Once used
substantively, a sheet's information structure is one
that allows input values to be changed, but more
extensive changes are complex. The premature
commitment and viscosity combined, result in users
becoming locked-in to early solutions and the
subsequent attempt to refine/improve them. These
points are evident anecdotally from businesses and
professionals who have working spreadsheets. In
many cases they are rarely refined or modified
because of the risk of 'breaking' a working, but
opaque, 'solution'.
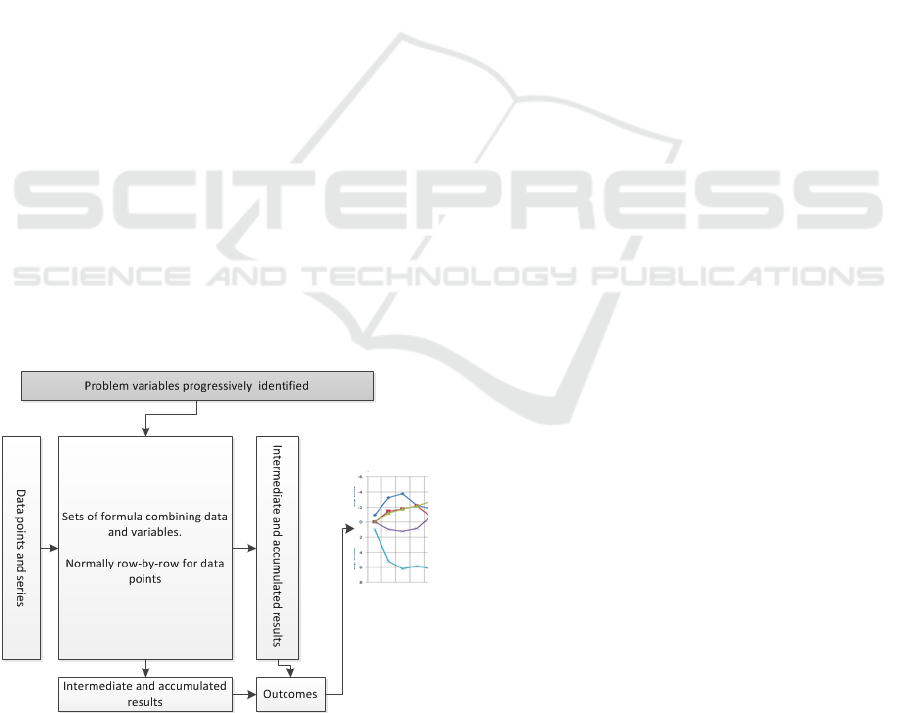
Figure 1: Schematic of spreadsheet base modelling.
2.2 Educational Uses
Similar factors are addressed in the early educational
use of spreadsheets keeping to rigid solution styles.
As part of our preliminary research, teaching and
assessment materials related to spreadsheet skills
were reviewed. This, in combination with
conversations with tutors, showed that spreadsheet
skills were focused largely upon following a given
model, structure and layout. This focus upon
prescribed solutions leaves little opportunity for
exploratory modelling or problem solving that could
depart from given examples.
2.3 Exploration and Development
When used in model development, the 'locking-in'
effect of spreadsheets is a powerful influence. In
simple terms we can outline a spreadsheet model as
being equivalent to the structure in figure 1.There
are variables (at the top) used in formula (central
rectangle) applied to input data (on the left). Model
outputs are accumulated in rows and/or columns
feed into summary statistics, results, reports or
graphs (on the right hand side). We believe these
structural features are common to spread modelling,
even though this specific layout many not be
followed.
The iterative process of development of a model
is one of introducing variables identified as
necessary to examine and capture emergent features.
In terms of our figure, reification tends to add more
subtle variables (at the top) and associated
computations (in the central rectangle). However,
structurally, the model output is already present (on
the right hand side). Hence, as opposed to re-
designing a sheet's structure with each new variable
introduced, the formulas used rise in complexity to
accommodate new variables.
Note that this account of use is the antithesis of
skills based training where the variables, layout and
requirements are all prescribed beforehand.
2.4 Example
We illustrate our account of iterative modelling with
a work based training example set in the domain of
construction. It concerns the cost of tiling an
irregular floor shape - in this case an "L" shaped
room. The floor area can be treated as three adjoined
rectangles (2m x 3m, 3m x 3m and 3m x 1m). So,
assuming the price per 1m x 1m tile is given as, say,
4.99 euros the total cost of the tiles would be:
=4.99*(2*3+3*3+3*1)
CSEDU 2016 - 8th International Conference on Computer Supported Education
384

Educationally, progressive modelling could include
recognising that the price of a tile is a variable that
can be kept in cell for that purpose (say, A2). In
which case the formula would become:
=A2*(2*3+3*3+3*1)
Similarly, these tiles are a specific size. Other tiles
may be of a different size. In that case another
variable, the area of a tile may be kept in, say, A3
and formula updated to:
=A2*(2*3+3*3+3*1)/A3
A delivery charge can be modelled too as a fixed
amount added to the total:
=A4+A2*(2*3+3*3+3*1)/A3
While this is clearly a simple numeric problem it
illustrates the rise in complexity. If the model goes
on to account for, say, free delivery with orders over
a certain amount, then the formula becomes more
complex.
= (A2*(2*3+3*3+3*1)/A3) +
IF((A2*(2*3+3*3+3*1)/A3) > A5, 0, A4)
Other factors as they are recognised will add further
complexity to what was at first a very simple model.
This incremental model development will not
necessarily be well designed or structured because of
the factors emerging during its development. What
is more, hand-in-hand with this growing formula
complexity is the difficulty of seeing formula errors
and errors in the resulting outputs.
3 VISUALISATION
Graphical representations, such as flowcharts, and
pictorial representations of data structures have long
been used to support the understanding of programs
and their underlying processes (Myers 1986).
However, it is of interest to note that in visual
computational language the empirical evidence of
their compelling and appealing character is limited,
as is their educational utility (Sorva, et al. 2013).
Previous work has proposed ways of presenting
and visualizing spreadsheets, see: Saariluoma and
Sajaniemi (1991), Igarashi, et al. (1998), Ballinger,
et al. (2003) and Burnett, et al. (2001). However
these works only consider the wider structure of
spreadsheets, and the dependencies between cells.
None appear to have addressed the fact that the
formulas language is computationally powerful but
contracted onto a single line. It is this complexity of
language presentation that can complicate its
effective use. Our enhanced spreadsheet tool
employs a visual language that graphically
represents spreadsheet formulae.
A visualisation offers a ‘scaffold’ of geometric
forms, colours and connectors that take advantage of
human perceptual ability to recognise patterns and
associations - and support “visual thinking”. We aim
to make the relationship and sequence of formulae
elements more evident and immediate using such
techniques. Examples of how this might reveal itself
include: learners recognising when a formula result
is not fit for its intended purpose; identifying where
an error is in a formula, or; identifying what
modifications are necessary to ensure a formula does
work. For example, if a cell is computing an
unexpected result, the learner will need to closely
inspect the formula and essentially ‘debug’ it. With
good visual 'scaffolding', any problem in the formula
should be more easily identified.
3.1 The Designing a Visual Language
The visualisations were developed on paper to allow
the authors, tutors and learners to explore and
provide rapid feedback on which visual
characteristics are appropriate and of value. Initially
good visual design practice was followed, informed
by learning scenarios and educational uses of
spreadhseets (e.g. see: Gretton and Challis, 2008).
The principles for the initial design phase where:
– Evidencing structure. Within a given formula,
the syntactic structure is core to comprehending
meaning.
– Visual mapping. The ease of mapping between
the formula and visualisation. Clearly, if this
mapping is complex for a learner, the
visualisation may be of little value.
– Evidencing categories. Within a given formula,
being able to recognise the different categories
of tokens and structures.
– Evidencing abstractions. There are various
abstractions apparent in the way formulae are
used. For example, the same sub-expression
appearing in a number of places in a single
formula. A simple example would be the
formula for a quadratic, such as,
=A1*X1*X1+B1*X1+C1. The repeated use of
X1 is important for understanding what is
expressed. A more complex abstraction is the
repeated use of the expression (2*3+3*3+3*1),
in the simple example above.
– Evidencing computation. In contrast to
abstractions, there is the value of evidencing the
specific values used in determining the resulting
value of a formula. Hence, when a formula such
Visualising Formula Structures to Support Exploratory Modelling
385

as, =2+3*4 produces the result 14, it is important
to understand that arises form 2+12 and the 12
arises from 3*4.
– Visual simplicity and scalability. Although not
easily defined, this principle discourages
apparently empty space, redundant arcs or
overlapping lines or structures. In view of our
motivation, this point is most relevant for
complex formulae.
Two visualisation approaches were identified:
‘Explicit Visualisation’ (EV), and; ‘Dataflow
Visualisation’ (DV). Both were based on a data flow
metaphor with components interconnected by flows
that represented results passing between operations
within a formula. Both also presumed a top-down
reading with the starting expression at the top and
the outcome at the bottom. Categories of node
included: numeric values, cell references, strings,
operators and built-in spreadsheet functions, with all
such types being given a distinct visual identity.
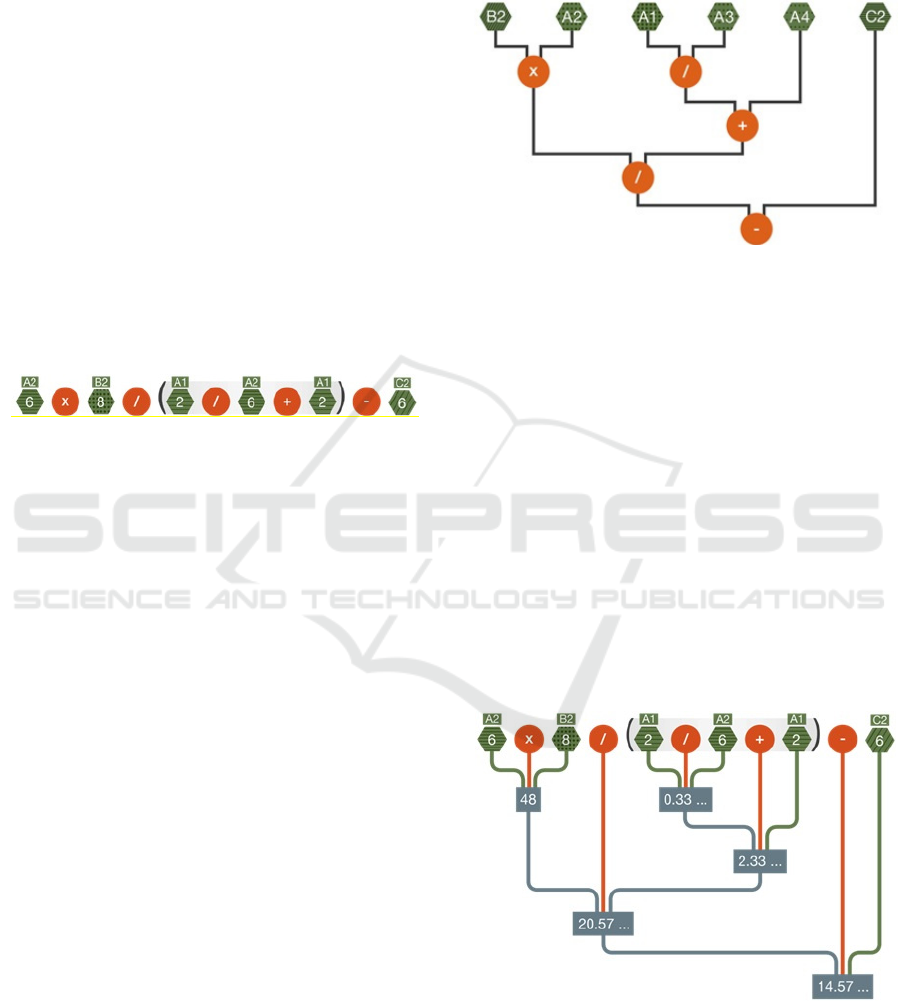
Figure 2: An initial tokenised visualisation of a formula
=A2xB2/(A1/A2+A1)-C2 as graphical tokens.
3.2 Dataflow Visualisations
The Dataflow Visualisation (DV) focuses an abstract
view based upon the rationale that the formula
structure is key to assessing its correctness.
Specifically DV was based upon the following rules:
– Cell references are not replaced by their numeric
values, as the presence of a value (and not the
literal amount) which is important to the model.
– The outputs from functions and operations
consistently flow down any functions that use
them as inputs.
– Brackets are not used, as operator scoping can be
inferred by the order of operations represented
by the visualisation. The reduced number of
visual elements supports visual simplicity and
scalability.
DV emphasises formula structure, and minimises
numeric details. The rationale behind this is that a
'wrong' formula is because of it not linking its
components correctly. Hence, displaying the
structure in this way will help identify important
errors or slips. It captures what is being proposed as
a solution and not the details of any specific instance
of the solution. For an example of DV see figure 3.
In terms of our initial principles, evidencing
visual mapping is weak since the formula as typed in
the spreadsheet cannot be immediately obvious in
the visualisation. In addition, the evidencing of
computation is relatively weak since the flow is
shown but not the effect of individual operations or
functions.
Figure 3: A DV visualisation of the expression in figure 2.
3.3 Explicit Visualisation
Unlike DV, the Explicit Visualisation (EV) approach
graphically represented each computation step in
processing a formula:
– The visualised formula is a direct match to the
original spreadsheet formula. Thus supporting
the concept of visual mapping.
– Cell references include the numeric values in
those cells. While this detracts from the visual
mapping it does support evidencing of basic
computations.
– Values, functions and operators flow down into
additional nodes ("monitors") which themselves
show the result of the associated operator or
function applied to its arguments. This further
supports evidencing computation.
Figure 4: EV visualisation of the expression in figure 2.
3.4 Conditionals
One of the issues with complexity, illustrated
withour simple example, is the use of conditional
CSEDU 2016 - 8th International Conference on Computer Supported Education
386

functions (such as "IF"). Interestingly, conditionals
highlight basic tensions between the proposed
visualisation rules.
The most common conditional is the "IF"
function: "IF" takes three arguments, and behaves as
follows: if the first argument (the CONDITION) is
evaluated to TRUE, then the second argument (the
THEN-PART) is evaluated and the result is returned
as the value of the "IF" expression. Otherwise, the
third argument (the ELSE-PART) is evaluated and
that value is returned. Hence, they embody two
computational behaviours, when one is only ever
used. This poses an inherent problem when we
consider visualising computation behaviours.
This exposes the difficulties of visualising
conditionals in EV and DV. In the case of EV, a
non-computed ELSE-PART would need to be
shown and it would be necessary to indicate that its
value is not computed. However, the same formula
in the contrary case would show the THEN-PART
not computed (see figure 5). This dynamism is at
odds with the idea of a single representation for a
formula not itself changing.
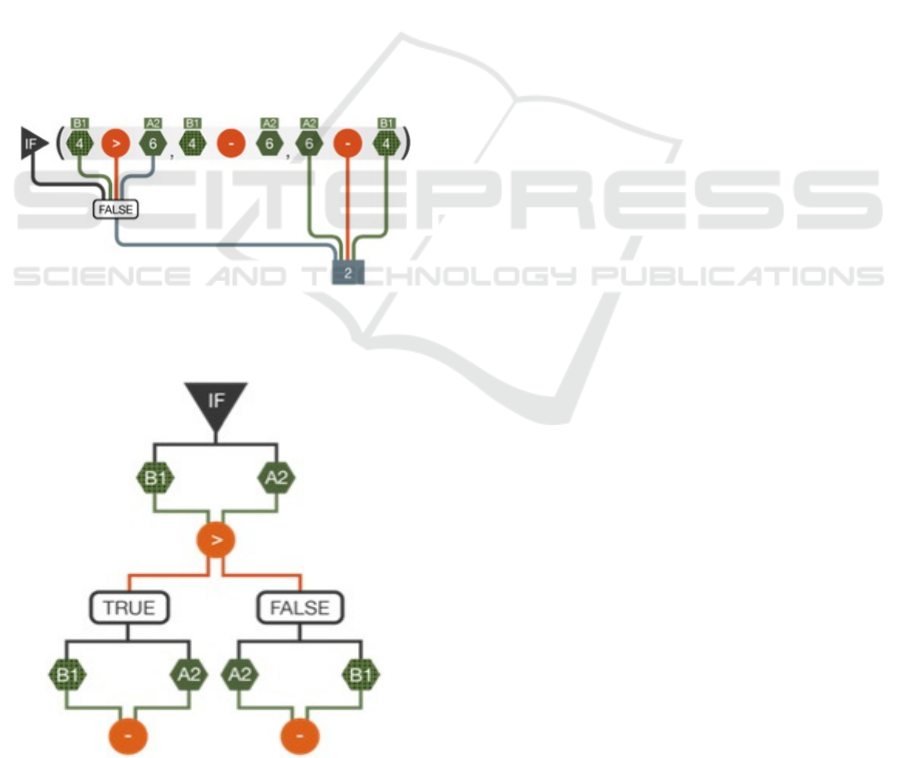
Figure 5: A simplistic EV visualisation of a conditional
expression, in which the THEN-PART is present but not
used.
Figure 6: A DV visualisation of a conditional expression,
illustrating the separation of flow into two alternate
computations.
4 EVALUATION
We conducted a variety of user studies. In keeping
with iterative design principles each study
considered both assessing the appropriateness of the
visualisations and also gathering formative
feedback. The primary target users were college
based learners developing skills for higher education
entry and improved employability.
In general, these evaluations faced
methodological challenges which limited the
scientific assessment of the visualisations. Firstly,
our target users despite using and learning about
spreadsheets had widely differing levels of
familiarity. This was partly due to: the stage and
structure of differing colleges; the differing
examination boards being used, and; the level of
staff engagement with the topic. In fact, the account
of modelling that we discussed earlier in this paper
was rarely apparent since teaching materials did not
encourage exploratory modelling per-se. A second
issue that limited controlled comparable assessment
of visualisations was that differing subjects had
differing approaches to using spreadsheets. For the
majority the default response was that spreadsheets
were "ICT" and as such were not readily used in
maths or science. In these cases consultation with
individual tutors was necessary to identify how to
harness spreadsheets as numeracy tools relevant to
specific topics.
4.1 Initial Evaluations
Initial evaluations were directed at assessing the
comprehension of the visualised formula with the
aim of comparing textual formula, DV and EV
(Leitão and Roast 2014).
Initially the two styles of visualisation DV and
EV were assessed with between groups with task
completion being observed and along with some
post task interviews. For individual classes, the
approach to user engagement varied in response to
the readiness of technology, users' academic levels,
and support of their tutor. This included:
– Paper based materials with multiple choice
formulae comprehensions tasks. This included:
(i) a formula and a number of possible results;
(ii) a mini-problem statement and a number of
formulae (one of which is correct for the
problem).
– Prototype implementations of DV and EV were
developed as extensions to an existing
spreadsheet package. With the prototype the
tasks were to construct or modify a formula in
Visualising Formula Structures to Support Exploratory Modelling
387

the spreadsheet to solve a set of mini-problems.
An example mini-problem is:
"Does =A1*(A1*A1) calculate cell A1 to the
power of 4? If not, correct the formula."
Performance was measured assessed by the number
of answers. Subjects varied in age profile, familiarity
with spreadsheets and readiness to engage with the
tasks. Quantitative results from these studies
(summarised in table 1) suffered from challenges
described above. However, the fact that learners
engaged with the tasks set and worked effectively
with the visualisations did show some positive
benefits and in no cases was there evidence of them
impairing the tasks set.
During the same period educational experts were
consulted regarding the tool and the visualisations
and encouraged to critic the approach takes.
Feedback from this process and interviews with
subjects were valuable in helping distinguish
between DV and EV.
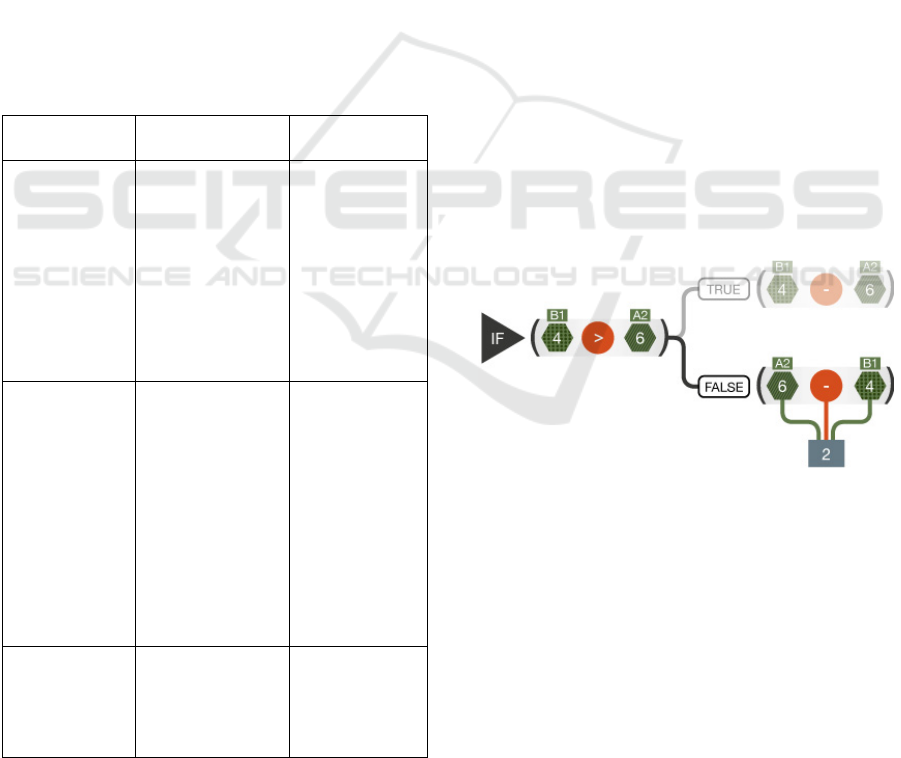
Table 1: Summary of initial evaluation studies and
outcomes.
Study Population and
context
Outcome
Paper based
study with 8
spreadsheet
comprehension
questions.
44 work-based
learners studying
Electrical
engineering,
Engineering and
Maths at NVQ
level 3.
Visualisation
showed a
positive effect.
Average score
was 55% with a
visualisation,
and 51%
without.
(Not
significant)
Interactive
prototype
based study
and qualitative
inter-views
14 full-time
learners were
given a
spreadsheet
"refresher" and
then completed
37 spreadsheet
formula questions
Visualisation
conditions
showed a
positive effect
over the no-
visualisation
condition.
Average score
73% with a
visualisation,
and 67%
without
Interviews and
demonstration
with experts.
Three STEM
educators, three
STEM education
researchers and
five support staff
Initial evaluation stage outcomes were that the
explicit EV style was of more value. The support for
evidence of computation and mapping back to the
spreadsheet formula counted highly for educational
experts, tutors and learners.
Feedback on visualisation of conditionals was
not so straight forward partly due to learners and
tutors being less familiar with using conditionals.
Hence the outcome was to review the visualisation
taking into account the general points arising from
the evaluation of DV and EV.
4.2 Design, Development and
Evaluation
Following the initial development and evaluation we
developed a more robust prototype tool suitable for
broader scale trialling and assessment. This also
involved integrating with the most widely used
spreadsheet, specifically MS Excel (Campbell-
Kelly, 2007).
The visualisation developments focused upon
developing an EV-based visualisation of
conditionals that aimed to ensure a good mapping
with the formula while indicating the dynamic
character of conditional behaviour. The resulting
visualisation is illustrated in figure 7. In this design
the THEN-PART and the ELSE-PART are shown,
but in addition, the un-used part is faded to indicate
it is not in use and the conditional expression is
shown to be "selecting" the relevant part.
Figure 7: The revised EV style visualisation of
conditionals.
The value of having the prototype tool working
with the most common spreadsheet benefited the
next evaluation activity. In this case cohorts of
learners studying functional skills in various areas
were approached and introduced to the tool. Where
possible, this introduction mapped to their existing
use of spreadsheets, such as their current topics of
study or tutorial work.
The initial evaluation was taken to have
demonstrated that our general approach visualisation
was valid. However, evidencing performance
improvements attributable to the visualisation was
CSEDU 2016 - 8th International Conference on Computer Supported Education
388

judged to be too methodologically complex, for the
reasons described earlier. As a consequence the
second phase of evaluation focused upon whether
the prototype technology was recognised by users to
be of potential value. It was assumed that this
judgement could be made by users, even if the tool
was not used comprehensively in the sessions when
it was introduced to them. For this reason the
Technology Adoption Model (Davis, et al. 1989)
was used to develop a series of questions for both
learners and tutors.
Over 15 learners were introduced to the tool
during a taught element of work related courses.
They subsequently attempted specified spreadsheet
tasks at a level matching their normal class. The
tasks lasted for between 30 and 60 minutes, during
which they worked with the tool running with MS
Excel. Responses were gathered on a Likert scale
questions (1 to 7). The most positive responses were
with respect to the visualisation (6.17) and
responsiveness of the system (6.00). The least
positive response (3.92) was just below the median
of 4.00, and concerned whether learners perceived
the tool as helping them work more efficiently.
As with the initial evaluation, the results are on
the whole positive for a small number of subjects.
Qualitative feedback supports this view:: "It would
help me a lot with other formulas", "You can see the
values and how they are worked out, that's great."
and "It would help anyone willing to learn about
spreadsheets".
In addition supportive qualitative evidence came
from tutors engaged during the sessions: "I am sure
that it could add value to the teaching of
mathematics."; "I think it would be very helpful";
"Absolutely brilliant when it comes to more
complicated formulas for our learners. With
regards to the IF statement, I particularly like the
way it checks the condition and identifies whether it
is TRUE or FALSE. Additionally really good for
formulas of non-adjacent cells."
Both tutor and learner feedback also supported
identifying additional visualisation details. One
example of this was the need in complex cases to
indicate the flow of data more explicitly, as well as
the final result node. Features such as these were
introduced to the next iteration of the tools which
currently under going evaluation.
5 DISCUSSION
Despite the lack of familiarity with the
visualisations, their presence and use did not impair
learner performance. In follow-on interviews all
agreed that the visualisation approach had merit.
Overall feedback was positive, with those
interviewed seeing the potential to help "de-mystify"
spreadsheets for learner population we are targeting.
For example, trainee tutor commented:
"I struggle a lot with spreadsheets and find it
hard to understand them. Seeing the spreadsheet
visualisation prototype made it clearer to
understand the formulas and feel that if I had chance
to use a programme of that kind I would have a
greater understanding and be able to pick up the
skills I require much quicker. I feel that this product
could help people like myself that struggle with
spreadsheets."
An expert in maths education research
commented:
“It will be very useful to many students to have a
product that enables a better conceptual
understanding of the equation format. There is a
clear need for such a tool to be suitable for the many
students who do not have high levels of
mathematical skills and yet use mathematical
symbolism every day in their studies. This will
include students from Chemistry, Business,
Economics, Psychology, Geography and many
more."
6 FUTURE WORK AND
CONCLUSIONS
We have reported the iterative development of the
visualisation tool in terms of: preliminary design,
initial development and evaluation and then the
evaluation of prototype operating with MS Excel.
This is part of an on going process of evaluation and
refinement, with learner and tutor feedback
informing future enhancements.
The widespread use of spreadsheets in work and
education (Chambers and Scaffidi, 2010) may pose
significant barriers to learners. This limits their
potential benefit as a tool for exploring STEM
related topics is limited. Our approach to visualising
formulae, offers a means of helping learners work
more effectively with spreadsheets. Evidence of the
benefit of this approach is positive but it requires
further investigation. Similarity the principles that
underpin the effectiveness of the visualisation
language require further development, specifically to
address some of the more complex structures found
in spreadsheet formula.
The long-term b enefit of making spreadsheets
Visualising Formula Structures to Support Exploratory Modelling
389

more usable is one that could impact upon academic
progress for individuals as well as general numeracy
skills. The value of the resulting improved ability
aligns to national and international educational
objectives regarding skills and employability.
ACKNOWLEDGEMENTS
We are indebted to local colleges' staff and students
that were willing to support and participate in the
studies reported. The technical development of the
tool benefited significantly from the technical
contribution of Tony Day. This work is supported in
part by: UK Higher Education Academy and The
Small Business Research Initiative (part of Innovate
UK).
REFERENCES
Ballinger, D., Biddle, R. and Noble, J., 2003. Spreadsheet
structure inspection using low level access and
visualisation. In Proc. Fourth Australasian User
Interface Conference (AUIC2003). Biddle, R. and
Thomas, B., Eds. ACS. 91-94.
Blackwell, A.F., Britton, C., Cox, A. Green, T.R.G., Gurr,
C.A., Kadoda, G.F., Kutar, M., Loomes, M., Nehaniv,
C.L., Petre, M., Roast, C., Roes, C., Wong, A. and
Young, R.M., 2001. Cognitive Dimensions of
Notations: Design tools for cognitive technology. In
M. Beynon, C.L. Nehaniv, and K. Dautenhahn (Eds.)
Cognitive Technology 2001 (LNAI 2117). Springer-
Verlag, pp. 325-341.
Burnett, M., Atwood, J., Djang, R., Gottfried, H.,
Reichwein, J. and Yang, S., 2001. Forms/3: A first-
order visual language to explore the boundaries of the
spreadsheet paradigm. Journal of functional
programming 11(2): 155-206.
Burnett, M., Sheretov, A., Ren, A. and Rothermel, G.,
2002. Testing homogeneous spreadsheet grids with the
"what you see is what you test" methodology," IEEE
Trans. Softw. Eng., 28(6) pp. 576-594.
http://dx.doi.org/10.1109/TSE.2002.1010060.
Campbell-Kelly, M.,2007. Number crunching without
programming: The evolution of spreadsheet usability.
IEEE Annals Of The History Of Computing, 29(3),
pp.6-19, ISSN: 1058-6180.
Chambers, C. and C. Scaffidi (2010). Struggling to excel:
A field study of challenges faced by spreadsheet users.
Visual Languages and Human-Centric Computing
(VL/HCC), 2010 IEEE Symposium on, IEEE.
Davis, F.D., Bagozzi, R.P. and Warshaw P.R., 1989. User
acceptance of computer technology: A comparison of
two theoretical models. Management Science, 35 (8)
pp. 982–1003.
Gretton, H. and Challis, N., 2008. "Fundamental
Engineering Mathematics; A Student Friendly
Workbook" Woodhead Publishing, 2008, ISBN-13:
978-1898563655.
Hendry, D.G. and Green, T.R.G., 1994. "Creating,
comprehending and explaining spreadsheets: a
cognitive interpretation of what discretionary users
think of the spreadsheet model." in International
Journal of Human-Computer Studies, 40(6), 1033-
1065, DOI=10.1006/ijhc.1994.1047.
Igarashi, T., Mackinlay, J.D., Chang, B-W and Zellweger,
P.T., 1998. Fluid Visualization of Spreadsheet
Structures, Proceedings of the IEEE Symposium on
Visual Languages, p.118.
Leitão,R. and Roast, C., 2014. Developing visualisations
for spreadsheet formulae: towards increasing the
accessibility of science, technology, engineering and
maths subjects. In: 9th Workshop on Mathematical
User Interfaces, Coimbra, Portugal, 10 July 2014.
Myers, B. A. (1986). Visual programming, programming
by example, and program visualization: a taxonomy.
ACM SIGCHI Bulletin 17(4): 59-66.Panko, R. R.,
2008. What We Know About Spreadsheet Errors.
Journal of End User Computing's Special issue on
Scaling Up End User Development
10, 15-21.
Panko, R. R. and Sprague Jr., R. H., 1998. "Hitting the
wall: errors in developing and code inspecting a
simple spreadsheet model" Decision Support Systems
22(4): 337-353.
Peyton Jones, S., Blackwell, A. and Burnett, M., 2003. A
user-centred approach to functions in Excel. In
Proceedings of the eighth ACM SIGPLAN
international conference on Functional programming
(ICFP '03). ACM, New York, NY, USA, 165-176.
DOI=10.1145/944705.944721.
Rello, L., Kanvinde, G. and Baeza-Yates, R., 2012.
Layout guidelines for web text and a web service to
improve accessibility for dyslexics. Proceedings of the
International Cross-Disciplinary Conference on Web
Accessibility, ACM.
Saariluoma, P., Sajaniemi, J.,1991. Extracting Implicit
Tree Structures in Spreadsheet Calculation.
Ergonomics 34(8), 1027-1046.
Sajaniemi, J., 2000. Modeling Spreadsheet Audit: A
Rigorous Approach to Automatic Visualization,
Journal of Visual Languages and Computing. 11, 49-
82. doi:10.1006/jvlc.1999.0142.
Sorva, J., Karavirta, V. and Malmi, L., 2013. A Review of
Generic Program Visualization Systems for
Introductory Programming Education. Trans. Comput.
Educ. 13, 4. DOI=http://dx.doi.org/10.1145/2490822.
Stein, J. and V. Walsh, 1997. "To see but not to read; the
magnocellular theory of dyslexia." Trends in
neurosciences 20(4): 147-152.
Technology Insights 2012, e-skills UK (Available at
http://www.e-skills.com).
CSEDU 2016 - 8th International Conference on Computer Supported Education
390