An Interval Type-2 Fuzzy Logic System for Assessment of Students’

Answer Scripts under High Levels of Uncertainty

Ibrahim A. Hameed

1,*

, Mohanad Elhoushy

, Belal A. Zalam

and Ottar L. Osen

Department of Automation Engineering (AIR), Faculty of Engineering and Natural Sciences,

Norwegian University of Science and Technology (NTNU), Larsgårdsvegen 2, 6009 Ålesund, Norway

Department of Industrial Electronics and Control Engineering, Faculty of Electronic Engineering,

Menofia University, 32952 Menouf, Egypt

Key

words: Students’ Evaluation, Uncertainty, Interval Type-2 (IT2) Fuzzy Sets, Type Reduction, Footprint of

Uncertainty (FOU).

Abstract: The proper system for evaluating the learning achievement of students is the key to realizing the purpose of

education and learning. Traditional grading methods are largely based on human judgments, which tend to

be subjective. In addition, it is based on sharp criteria instead of fuzzy criteria and suffers from erroneous

scores assigned by indifferent or inexperienced examiners, which represent a rich source of uncertainties,

which might impair the credibility of the system. In an attempt to reduce uncertainties and provide more

objective, reliable, and precise grading, a sophisticated assessment approach based on type-2 fuzzy set

theory is developed. In this paper, interval type-2 (IT2) fuzzy sets, which are a special case of the general

T2 fuzzy sets, are used. The transparency and capabilities of type-2 fuzzy sets in handling uncertainties is

expected to provide an evaluation system able to justify and raise the quality and consistency of assessment

judgments.

1 INTRODUCTION

As highlighted by Boud (1988), assessment methods

and requirements probably have a greater influence

on how and what students learn than any other

factor. This influence may become of greater

importance than the impact of teaching materials

itself. A high quality, reliable and transparent

assessment system supports and improves student

lifelong learning and ensures that all students receive

fair treatment in order not to limit students' present

and future opportunities. The evaluation of a

students’ learning achievement is done over years

and provides the basis for certification of individual

achievement, therefore, it should regularly reviewed

and improved to ensure that the systems are

educationally beneficial to all students (Saleh and

Kim, 2009; Hameed, 2011). Students’ evaluation

and scoring are largely based on human judgments,

which tend to be subjective, and hence represents a

rich source of uncertainties. Assessment process, as

well, is suffering from uncertainty due to assigning

erroneous grades and indifferent and inexperienced

practices. Uncertainty is an attribute of information

(Zadeh, 2005). More often than not, the decision-

relevant information is subjected to uncertainty

arising from different sources. Consequently,

decisions involve an undeniable amount of risk

(Daradkeh et al., 2013).

In an attempt to reduce the uncertainty in the

students’ assessment process, several attempts have

been made in the last decade to use fuzzy set theory

in educational evaluation. Biswas (1995) presented

two methods for students’ answerscripts evaluation

using fuzzy sets; a fuzzy evaluation method and a

generalized fuzzy evaluation method and a matching

function. Echauz and Vachtsevanos (1995) proposed

a fuzzy logic system for translating traditional scores

into letter-grades. Law (1996) built a fuzzy structure

model for education grading system with its

algorithm to aggregate different test scores in order

to produce a single score for individual student.

Wilson, Karr and Freeman (1998) presented an

automatic grading system based on fuzzy rules and

genetic algorithms. Chen and Lee (1999) presented

two methods for applying fuzzy sets to overcome the

problem of rewarding two different fuzzy marks the

same total score that could arise from Biswas’

Hameed, I., Elhoushy, M., Zalam, B. and Osen, O.

An Interval Type-2 Fuzzy Logic System for Assessment of Students’ Answer Scripts under High Levels of Uncertainty.

In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016) - Volume 2, pages 40-48

ISBN: 978-989-758-179-3

method. Ma and Zhou (2000) proposed a fuzzy set

approach to assess the outcomes of student-centered

learning using the evaluation of their peers and

lecturer.

Weon and Kim (2001) presented an evaluation

strategy based on fuzzy MFs. They pointed out that

the system for students’ achievement evaluation

should consider the three important factors of the

questions that the students answer: the difficulty, the

importance, and the complexity. Weon and Kim

used singleton functions to describe the factors of

each question reflecting the effect of the three

factors individually, but not collectively. Wang and

Chen (2008) presented a method for evaluating

students’ answerscripts using fuzzy numbers

associated with degrees of confidence of the

evaluator. Bai and Chen (2008b) pointed out that the

difficulty factor is a very subjective parameter and

may cause an argument about fairness in evaluation.

Bai and Chen (2008a) proposed a method to

automatically construct the grade MFs of fuzzy rules

for evaluating student’s learning achievement. Bai

and Chen (2008b) proposed a method for applying

fuzzy MFs and fuzzy rules for the same purpose. To

solve the subjectivity of the difficulty factor of

Weon and Kim’s method (2001), they obtained the

difficulty as a function of accuracy of the student’s

answer script and time consumed to answer.

However, their method still has the subjectivity

problem, since the results in scores and ranks are

heavily depend on the values of several weights that

are determined by the subjective knowledge of

domain experts.

Saleh and Kim (2009) proposed three nodes

fuzzy logic approach based on Mamdani’s fuzzy

inference engine and the center of gravity (COG)

defuzzification technique as an alternative to Bai and

Chen’s method (2008b). The transparency and

objective nature of the fuzzy system makes their

method easy to understand and enables teachers to

explain the results of evaluation to persuade skeptic

students. Hameed (2011) proposed using Gaussian

MFs as an alternative of the triangle MFs used in

Saleh and Kim (2009). A sensitivity study showed

that using Gaussian MFs with standard deviation

higher than 0.4 provide more reliable and robust

evaluation system which is able to provide new

ranking orders without changing students’ scores.

In this paper, a type-2 fuzzy logic (T2FL) system

is proposed. The general framework of T2 fuzzy

reasoning allows handling much of the uncertainty

inherited in students’ evaluations systems. T2FL has

better capabilities in reducing the amount of

uncertainty in a system due to its ability in handling

linguistic uncertainties by modeling vagueness and

unreliability of information (Liang and Mendel,

2000). In this paper, a new implementation of the

three-nodes fuzzy evaluation system presented in

Saleh and Kim (2009) and Hameed (2011) using

T2FSs will be presented. An example will be given

to highlight the differences between traditional,

T1FSs- and T2FSs-based approaches.

The paper is organized as follows: a review of

some existing evluation approaches is presented in

Section 2. The proposed inteleval type-2 fuzzy logic

based evalaution system is presented in Section 3. In

Section 4, results of the appraoches presented in

Sections 2 and 3 applied to a real world example are

presnted. Comaprsons between different approahces,

concluding remarks and future work are presnted in

Section 5.

2 REVIEW OF EVALUATION

METHODS

2.1 Classical Approach

Assume that there are n students to answer m

questions. Accuracy rates of students’ answerscripts

(student’s scores in each question divided by the

maximum score assigned to this question) are the

basis for evaluation. We get an accuracy rate matrix

of dimension m x n,

A = [a

], m x n,

where

]1,0[∈

denotes the accuracy rate of

student j on question i. Time rates of students (the

time consumed by a student to solve a question

divided by the maximum time allowed to solve this

question) is another basis to be considered in

evaluation. We get a time rate matrix of dimension

m x n,

T = [t

], m x n,

where

]1,0[∈

denotes the time rate of student j

on question i. We are given a grade vector

G = [g

], m x 1,

where

]100,1[∈

denotes the assigned maximum

score of question i satisfying

∑

100

Based on the accuracy rate matrix A and the grade

vector G, we obtain the total score vector of

dimension n x 1,

An Interval Type-2 Fuzzy Logic System for Assessment of Students’ Answer Scripts under High Levels of Uncertainty

S = A

G = [s

], n x 1, (1)

where s

]100,0[∈

is the total score of student j

which is obtained by

∑

⋅

iij

(2)

The classical rank of students is then obtained by

sorting values of S in a descending order. In this

approach, the time used in solving each question is

not considered

2.2 Three-nodes Fuzzy Evaluation

Approach

The system consists of three nodes, the difficulty

node, the cost node, and the adjustment node, as it is

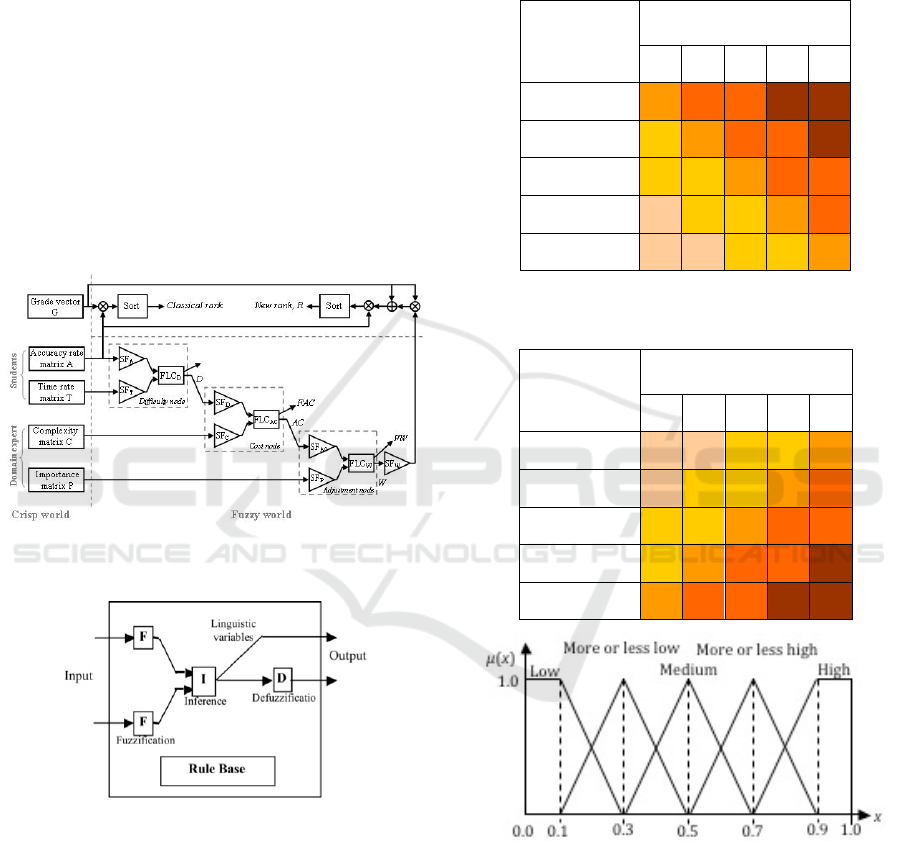
shown in Figure 1 (Saleh and Kim, 2009).

Figure 1: Block diagram of the three nodes fuzzy

evaluation system.

Figure 2: Node representation as a fuzzy logic controller.

Input to the system, in the left part of the figure,

is given either by exam results or domain expert.

Each node of the system behaves like a fuzzy logic

controller (FLC) with two scalable inputs and one

output, as it is shown in Figure 2. It maps a two-to-

one fuzzy relation by inference through a given rule

bases, shown in Tables 1 & 2 where 1, 2, 3, 4 and 5

stands for the five linguistic labels or levels low,

more or less low, medium, more or less high and

high. Fuzzy sets (FSs) are sets whose elements have

degrees of membership, and were first introduced by

Zadeh in 1965 as an extension of the classical notion

of set (Zadeh, 1965). The inputs are fuzzified based

on the predefined defined levels (fuzzy sets) shown

in Figure 3.

Table 1: A fuzzy rule base to infer the difficulty.

Accuracy

Time rate

1 2 3 4 5

1 3 4 4 5 5

2 2 3 4 4 5

3 2 2 3 4 4

4 1 2 2 3 4

5 1 1 2 2 3

Table 2: A fuzzy rule base to infer the cost and

adjustment.

Difficulty/

Cost

Complexity/

Importance

1 2 3 4 5

1 1 1 2 2 3

2 1 2 2 3 4

3 2 2 3 4 4

4 2 3 4 4 5

5 3 4 4 5 5

Figure 3: Triangular membership functions of the five

levels (i.e., five MFs).

In the first node, both inputs are given by exam

result, whereas in the later nodes, one input is the

output of its previous node while a domain expert

gives the other input. The output of each node can be

in the form of a crisp value (defuzzified) or in the

form of linguistic variables (MFs). Each node has

two scale factors (SFs) that can be chosen in a

manner to reflect the degree of importance of each

CSEDU 2016 - 8th International Conference on Computer Supported Education

input. Here, SFs are chosen to be equal to 1 to reflect

the equal influence of each input on the output. In

this method, each fuzzy node proceeds in following

four steps.

Step. 1: Fuzzification step in which inputs, if

given in crisp values, the degree to which these

inputs belong to each of the appropriate fuzzy sets is

determined. Triangular MF is the commonly used

due to its simplicity and easy computation. We note

that the same five fuzzy sets, shown in Figure 3, are

applied to represent the accuracy, the time rate, the

difficulty, the complexity, and the adjustment of

questions in the fuzzy domain.

Step. 2: Rule evaluation where the fuzzified

inputs are applied to the antecedents of the fuzzy

rules to obtain a single number that represents the

result of the antecedent evaluation (i.e., rule or firing

strength). The result of the antecedent evaluation is

then applied to the membership function of the

consequent (i.e., rule implication). Two implication

methods are commonly used; clipping where the

consequent membership function is sliced at the

level of the level of the rule firing strength. The

clipped function set loses some information,

however, it is preferred because it involves less

complex computations and generates an aggregated

output surface that is easier to defuzzify (Iancu,

2012). Another method, named scaling, offers a

better approach for preserving the original shape of

the fuzzy set: the original membership function of

the rule consequent is adjusted by multiplying all its

membership degrees by the truth value of the rule

antecedent

Step. 3: Aggregation of rule outputs where the

membership functions of all rule consequents

previously clipped or scaled are combined into a

single fuzzy set. Implication is modeled by means of

minimum operator, and the resulting output MFs are

combined using maximum operator (i.e.

aggregation).

Step. 4: defuzzification in which the aggregated

fuzzy sets are converted into a single crisp output.

The most popular method is the centroid technique

where a point representing the center of gravity

(COG) of the aggregated fuzzy set is found. In this

paper, the center of gravity (COG) method is

applied. The crisp value of question i is then

obtained by

(3)

where integrals are taken over the entire range of the

output and µ(x), and µ(x) is the membership degree

of x. By taking the center of gravity, conflicting

rules essentially are cancelled and a fair weighting is

obtained.

Each of the three nodes follows the above

scheme. The difficulty node has two inputs, the

accuracy rate and the time rate, and one output of the

difficulty. The cost node has two inputs, the

difficulty and complexity, and one output of the

cost. The adjustment node has two inputs, the cost

and the importance, and one output of the

adjustment.

The adjustment vector, W, is then used to obtain

the adjusted grade vector of dimension m x 1,

m x 1, where is the adjusted grade of

question i, and is obtained using the formula:

),1(

iii

wgg +⋅=

(4)

It is then scaled to its total grade by using the

formula:

∑∑

⋅=

jii

gggg

~~~

(5)

Then we obtain the adjusted total scores of

students by,

GAS

(6)

The new rank of students is then obtained by

sorting values of

in a descending order.

2.3 Gaussian based Three Nodes Fuzzy

Evaluation Approach

The three nodes fuzzy evaluation system described

in Section 2.2 is based on the simple triangular-

shaped MF formed using straight lines. Triangular

MFs are defined by three scalar parameters a, b and

c. The parameters a and c locate the feet of the

triangle MF while b locates its peak. There is no way

to get its optimum values, however, they should be

chosen in a manner to provide a satisfying overlap

between different MFs. The simplicity of this

function makes it ideal for control applications

where computational power and resources are

crucial (Zhao and Bose, 2002). However, it was

noted that when theses parameters are changed

slightly, different ranking orders are obtained which

could impair the system’s reliability.

In order to avoid losing reliability and having a

robust evaluation system, it should be able to give

the same ranking orders without changing students’

scores and for various values of these parameters. In

this connection, Gaussian MFs are proposed

(Hameed, 2011). Gaussian MFs are suitable for

problems that require continuously differentiable

curves and smooth transitions between levels,

whereas triangular MFs do not have. Gaussian MFs

∫∫

dxxdxxxy )()(.

μμ

[

gG =

An Interval Type-2 Fuzzy Logic System for Assessment of Students’ Answer Scripts under High Levels of Uncertainty

are defined by two parameters; c which locates the

distance from the origin to the center of each MF

and σ which determines its width. Gaussian MFs is

one parameter less than that of the triangular MFs

which will lead to an evaluation system with 15 less

Degrees Of Freedom (DOF) and hence a more

robust performance (Zhao and Bose, 2002).

Gaussian MFs is defined as

(7)

where c

is the center (i.e., mean) and σ

is the width

(i.e., standard deviation) of the i

fuzzy set, which

has by nature, infinite support. Therefore, for

Gaussian MFs with wide widths it is possible to

obtain a membership degree to each fuzzy set

greater than 0 and hence every rule in the rule base

fires. Consequently, the relationship between input

and output can be described accurate enough. Here,

the centers of the five Gaussian MFs are chosen to

be the same as that of the triangular MFs shown in

Figure 3 (i.e. [0.1 0.3 0.5 0.7 0.9]). Gaussian MFs of

the five levels for σ=0.1 are shown in Figure 4.

Figure 4: Gaussian membership functions of the five

levels for σ = 0.1.

From Figure 4 it is obvious that Gaussian MFs

provide more continuous transition from one interval

to another and hence provides smoother control

surface from the fuzzy rules. The Gaussian based

fuzzy evaluation system was able to provide correct

ranking order of students with equal total scores

without changing the total mean scores of all

students and the score of each student for σ ≥ 4.0

(Hameed, 2011; Hameed and Sørensen, 2010).

3 INTERVAL T2FL SYSTEM

BASED EVALUATION SYSTEM

Interval type-2 fuzzy logic systems (IT2 FLSs) have

demonstrated better abilities to handle uncertainties

than their type-1 (T1) counterparts in many

applications (Wu, 2013). The concept of T2FSs was

first introduced by Zadeh in 1975 (Zadeh, 1975) as

an extension of the concept of an ordinary type-1

fuzzy set. Such sets are fuzzy sets whose

membership grades themselves are T1FSs instead of

crisp numbers in T1 FS. Interval type-2 (IT2) FSs

are T2 FSs whose memberships are intervals instead

of T1FSs in a general T2FS (Zadeh, 2005).

T2FSs are useful in such cases when it becomes

difficult to determine exact membership function for

a fuzzy set and hence are useful for incorporating

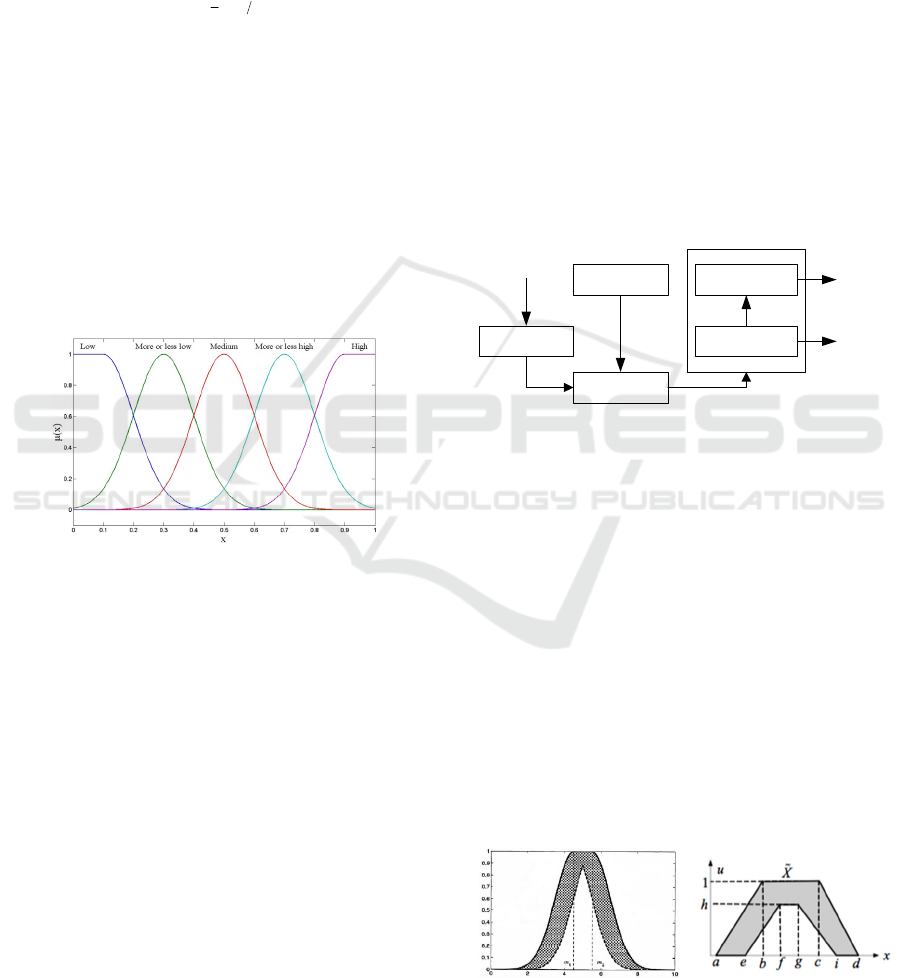
linguistic uncertainties. Figure 5 shows the

schematic diagram of an IT2 FLS. It is similar to its

T1 counterpart, shown in Figure 2, the major

difference being that at least one of the FSs in the

rule base is an IT2 FS. Hence, the outputs of the

inference engine are IT2FSs. A type-reducer is

needed to convert them into T1FSs before

defuzzification can be carried out (Wu, 2013).

Fuzzifier

Rules

Inference

Defuzzifier

Type Reducer

Output Processing

Fuzzy output setFuzzy input set

Crisp input Crisp output

Type reduced

set

Figure 5: Schematic diagram of IT2 FLS.

Mendel and Liang (1999) demonstrated the first

type-2 fuzzy framework where the information

about the linguistic/numerical uncertainty can be

incorporated. They introduced the concept of

concept of footprint-of-uncertainty (FOU) where the

an interval type-2 membership function (MF) is

characterized by an upper and lower type-1 MFs

bounding the region called FOU, as it is shown in

Figure 6. The internal structure of T2FLS is shown

in Figure 6. A fuzzy logic system can be considered

as T2 when at least one of the antecedents or

consequents of its rule-base’s FSs is T2. As the

outputs of the inference engine are IT2 FSs, a type-

reducer is required to convert its T2FSs into T1FSs

to be defuzzified. A detailed description can be

found in (Mendel, 2001).

(a) (b)

Figure 6: FOU for (a) T2 Gaussian MF, and (b) Triangle

MF.

()

−−

CSEDU 2016 - 8th International Conference on Computer Supported Education

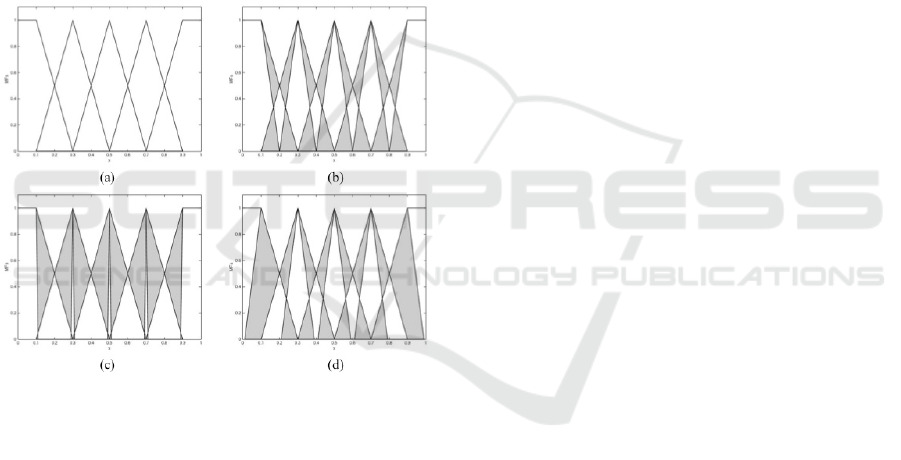
In this paper, the three-nodes fuzzy evaluation

framework shown in Figures 1 and 2 is implemented

using triangle T2FSs shown in Figure 6(b). Five T2

triangle MFs are used to represent the five levels

used to describe each variable, as it is shown in

Figure 7(a). The FOU (i.e., thickness of the MFs) is

provided as an external input by the domain expert

as an estimate of the amount of uncertainty in his/her

knowledge. In this paper, FOU is chosen to be a

number in the range of 0 to 0.3 where 0 refers to

zero uncertainty, 0.1 refers to low uncertainty, 0.2

refers to medium uncertainty and 0.3 refers to high

uncertainty. It is worth noting that the T2 fuzzy

system will converge to its T1 counterpart when

uncertainty measure is set to zero (Hameed, 2009),

as it is shown in Figure 7(a). In this paper, it is

assumed that the domain expert has a medium

degree of uncertainty in his knowledge (i.e.,

FOU≈0.2).

Figure 7: FOU: (a) zero uncertainty (FOU=0), (b) low

uncertainty (0<FOU≤0.1), (c) medium uncertainty

(0.1<FOU≤0.2), and (d) high uncertainty (0.2<FOU≤0.3).

4 RESULTS

In this section, a comparison between the different

evaluation approaches presented in Sections 2 and 3

will be introduced using an example.

4.1 Example

Assume that we have n students laid to an exam of m

questions where n=10 and m=5. The accuracy rate

matrix, A, the time rate matrix, T, and the grade

vector, G, are given as follows (Bai and Chen,

2008b; Saleh and Kim, 2009; Hameed, 2011):

61.097.051.039.093.065.081.008.049.093.0

25.09.092.032.002.05.016.018.072.073.0

74.091.042.087.086.017.071.097.069.077.0

53.081.022.004

.016.088.004.014.027.001.0

24.004.023.084.008.011.066.0135.059.0

⎥

⎦

⎤

⎢

⎣

⎡

2.08.02.08.016.0111.00

5.07.08.04.03.01101.02.0

4.01.03.02.019.01.001.00

3.008.02.03.013.09.001

9.04.06.

07.02.07.011.04.07.0

⎥

⎦

⎤

⎢

⎣

⎡

[]

3025201510=

Here, A=[a

] and T=[t

] are of n×m dimensions,

where a

∈[0, 1] denotes the accuracy rate of student

j on question i, t

∈[0, 1] denotes the time rate of

student j on question i. G

denotes the transpose of

G, where G is of m×1 dimension, G= [g

], g

∈[1,

100] denotes the assigned maximum score to

question i. Importance and complexity of each

question, I and C, are determined by the domain

expert as follows:

I =

00 0 0 1

0 0.33 0.67 0 0

0 0 0 0.15 0.85

10 0 0 0

0 0.07 0.93 0 0

⎡

⎣

⎢

⎤

⎦

⎥

C =

0 0.85 0.15 0 0

0 0 0.33 0.67 0

0 0 0 0.69 0.31

0.56 0.44 0 0 0

000.70.30

⎡

⎣

⎢

⎤

⎦

⎥

Matrices I=[i

] and C=[c

] are of dimension

m×l where i

∈[0, 1] denotes the membership value

of question i belonging to the importance level k,

and c

∈[0, 1] denotes the membership value of

question i belonging to the complexity level k.

4.2 Classical Approach

In this approach, total score can be obtained using

formula (1) as follows:

= 67.60 54.05 38.40 49.70 49.70 48.80 46.10 52.30 85.95 49.70

⎡

⎣

⎤

⎦

Thus the “classical” ranks of students can then

be obtained by simply sorting S in a descending

order to get:

> S

= S

> S

where S

> S

means score of student a is higher

than score of student b while S

= S

means that their

An Interval Type-2 Fuzzy Logic System for Assessment of Students’ Answer Scripts under High Levels of Uncertainty

scores are equal.

4.3 Triangle MFs based Fuzzy

Approach

The process starts by averaging the accuracy rate

and answer-time rate matrices A and T, respectively,

for each student to get:

= 0.45 0.31 0.711 0.47 0.637

⎡

⎣

⎤

⎦

= 0.57 0.48 0.31 0.50 0.57

⎡

⎣

⎤

⎦

Based on the fuzzy MFs shown in Figure 3 we

obtain the fuzzy accuracy rate matrix and the fuzzy

time rate matrix as follows:

FA =

0 0.25 0.75 0 0

0 0.95 0.05 0 0

0 0 0 0.945 0.055

0 0.15 0.85 0 0

0 0 0.315 0.685 0

⎡

⎣

⎢

⎤

⎦

⎥

035.065.000

00100

0005.095.00

009.01.00

035.065.000

⎥

⎦

⎤

⎢

⎣

⎡

=FT

In the first node, both inputs are given by

examination results, whereas in later nodes, one

input will be the output of its previous node and

while a domain expert will provide the other. The

output of each node can be in the form of a crisp

value (defuzzified) or in the form of fuzzy numbers

(i.e., degrees of membership (MFs) of each variable

in the five linguistic levels). Each node has two scale

factors (SFs shown in Figure 1). Here, we let both

scaling factors have the same value of unity

assuming equal influence of each input on the

output.

Each fuzzy node performs Mamdani fuzzy

inference to compute its output given the inputs and

the fuzzy rules (described in Tables 1 and 2). Each

fuzzy node proceeds in a number of steps described

in Section 2.2. By applying FA and FT to the first

node, the difficulty vector, D, and its fuzzy

counterpart, FD. In the same way, the cost vector

will be obtained by applying the difficulty and

complexity to the second node. Finally, the

adjustment vector, W, will be obtained by applying

the cost and importance to the third node as follows:

[]

5.0177.0749.0552.07.0=

The new scores of students S

to S

are then

obtained using Equations 3-5 to be 67.151, 53.168,

42.096, 52.190, 48.307, 51.814, 48.474, 49.272,

85.253, 51.493, respectively. The new rank of

students is then obtained by sorting values of

in a

descending order

> S

4.4 Gaussian MFs based Fuzzy

Approach

By replacing triangle MFs, used in Section 4.3,

which are formed simply using straight lines with

Gaussian MFs with the same center points (i.e.,

mean) as the triangle MFs, as it is shown in Figures

3 and 4 with stand deviation (i.e., width) σ≥4.0, new

scores for the 10 students are obtained where the

mean score is still equal to that of their original

scores obtained using the classical approach. The

new scores of students are then obtained using

Equations 3-5 as:

= 64.60 54.05 38.40 49.70 49.70 48.80 46.10 52.30 84.95 49.70

⎡

⎣

⎤

⎦

The new rank of students is then obtained by

sorting values of S in a descending

> S

Table 3: Ranking order for different FOU values.

FOU

Rank

1> 2> 3> 4> 5> 6> 7> 8> 9> 10

0 9 1 2 4 6 10 8 5 7 3

0.1 9 1 2 4 6 10 5 8 7 3

0.2 9 1 2 4 6 10 8 7 5 3

0.3 9 1 2 8 5 10 4 6 7 3

4.5 IT2 MFs based Fuzzy Approach

In this Section, IT2 MFs with different value of

FOU (i.e., zero, low, medium and high uncertainty)

as it is shown in Figure 7. The new ranking orders

for different FOU values are shown in Table 3. A

comparing between the ranking orders of the four

types is shown in Table 4.

Table 4: Ranking order for different approaches: class for

classical, T1T for type-1 triangle MFs, T1G for type-1

Gaussian MFs, and T2 for type-2 MFs.

Method

Rank

> 2> 3> 4> 5> 6> 7> 8> 9> 10

Class 9 1 2 8 4= 5= 10= 6 7 3

T1T 9 1 2 4 6 10 8 7 5 3

T1G 9 1 2 8 4 10 5 6 7 3

CSEDU 2016 - 8th International Conference on Computer Supported Education

T2 9 1 2 8 5 10 4 6 7 3

5 CONCLUSIONS

As it is shown in Table 1, classical assessment

approach resulted in students of equal scores that

make it difficult to determine a distinguished order

of each student. T1 Triangular FSs overcome the

problem of students of equal scores but at the same

time it changed scores of other students who does

not fall in that category which might spark questions

and make students skeptic about the evaluation

process. On the other hand, T1 Gaussian FSs based

system influenced only that category of students

with equal scores while other students of different

scores are left intact. Similarly, T2 FSs changed only

the scores and hence the rank order of students with

equal scores while the others are left intact. A major

difference between T2 and T1G FSs is that T2

system gave preferences to complexity of questions

over importance and that is clear from GIVING A

higher rank for student S5 who given a higher rank

(rank#5) on account of student S4 who is given a

lower rank (rank#7). On the other side, T1G gave

preferences to importance of questions over its

complexity and that explains why S4 is given higher

rank (rank#5) on account of S5 who has given a

lower rank (rank#7).

The transparency and the human logic nature of

fuzzy logic system make it easy to interpret and

explain why certain scores have changed. The

system inherently has a kind a feedback system to

correct erroneous scores assigned by indifferent or

inexperienced examiners. Easy of implementation of

the proposed system recommended it to spread out

and to be broadly used in other decisions support

systems. In this paper, a collective FOU for all the

fuzzy variables is used to represent a collective

uncertainty in the knowledge of the domain expert.

As a future work, the effect of using various FOU

values for each fuzzy variable such as importance,

complexity, etc. will be investigated. The evaluation

systems proposed in this paper hav been

implemented using the Fuzzy Logic Toolbox™ for

building a fuzzy inference system from

MathWorks™ (Fuzzy Logic Toolbox, 2016).

REFERENCES

Bai, S.-M., Chen, S.-M., 2008a. Automatically

constructing grade membership functions of fuzzy

rules for students’ evaluation. Expert Systems with

Applications, 35(3), 1408-1414.

Bai, S.-M., Chen, S.-M., 2008b. Evaluating students’

learning achievement using fuzzy membership

functions and fuzzy rules. Expert Systems with

Applications, 34, 399-410.

Biswas, R., 1995. An application of fuzzy sets in students’

evaluation. Fuzzy Sets and Systems, 74(2), 187-194.

Boud, D., 1988. Developing student autonomy in learning

ed.), London: Kogan Page.

Chen, S.M., Lee, C.H., 1999. New methods for students’

evaluating using fuzzy sets. Fuzzy Sets and Systems,

104(2), 209–218.

Daradkeh, M., McKinnon, A., Churcher, C., 2013.

Supporting informed decision-making under

uncertainty and risk through interactive visualization.

The Australian Computer Science Communications,

35(5), 23-32.

Echauz, J.R., Vachtsevanos, G.J. 1995. Fuzzy grading

system. IEEE Transactions on Education, 38(2), 158-

165.

Fuzzy Logic Toolbox™ 2.2.7, 2016, retrieved from

http://www.mathworks.com/products/fuzzylogic/ in

February 6

2016.

Hameed, I.A., 2009. Simplified architecture of a type-2

fuzzy controller using four embedded type-1 fuzzy

controllers and its application to a greenhouse climate

control system. Proc. IMechE Part I: Journal of

Systems and Control Engineering, 223(5), 619-631.

Hameed, I.A., 2011. Using Gaussian membership

functions for improving the reliability and robustness

of students' evaluation systems. Expert systems with

Applications, 38(6), 7135-7142.

Hameed, I.A., Sørensen, C.G., 2010. Fuzzy Systems in

Education: A More Reliable System for Student

Evaluation, Fuzzy Systems, Azar A. T. (Ed.), ISBN:

978-953-7619-92-3, INTECH, Croatia.

Iancu, I., 2012. A Mamdani type fuzzy logic controller,

Fuzzy Logic - Controls, Concepts, Theories and

Applications, Prof. Elmer Dadios (Ed.), ISBN: 978-

953-51-0396-7, InTech,

John, R.I., 1998. Type-2 fuzzy sets: an appraisal of theory

and applications. International Journal of Uncertainty,

Fuzziness Knowledge-Based Systems, 6(6), 563–576.

Larsen, P.M., 1980. Industrial applications of fuzzy logic

control. International Journal of Man-Machine

Studies, 12(1), 3–10.

Law, C.K., 1996. Using fuzzy numbers in education

grading system. Fuzzy Sets and Systems, 83(3), 311-

323.

Liang, Q., Mendel, J.M., 2000. Interval Type-2 Fuzzy

Logic Systems: Theory and Design. IEEE

Transactions on Fuzzy Systems, 8(5), 535-550.

Ma, J., Zhou, D., 2000. Fuzzy set approach to the

assessment of student-centered learning. IEEE

Transactions on Education, 43(2), 237-241.

Mamdani, E.M., 1974. Applications of fuzzy algorithms

for simple dynamic plants. Proceedings of the

Institution of Electrical Engineers (IEE), 21(2), 1585–

1588.

Mamdani, E.M., Assilian, S., 1975. An experiment in

linguistic synthesis with a fuzzy logic controller.

International Journal of Man-Machine Studies, 7, 1–

13.

An Interval Type-2 Fuzzy Logic System for Assessment of Students’ Answer Scripts under High Levels of Uncertainty

Mendel, J.M., 2001. Uncertain Rule-Based Fuzzy Logic

Systems, Prentice-Hall, Upper Saddle River, NJ 07458.

Mendel, J.M., Liang, Q., 1999. Pictorial Comparison of

Type-1 and Type-2 Fuzzy Logic Systems. In:

Proceedings of IASTED International Conference on

Intelligent Systems & Control.

Saleh, I., Kim, S.-I., 2009. A fuzzy system for evaluating

students’ learning achievement. Expert systems with

Applications, 36(3), 6236-6243.

Wang, H.Y., Chen, S.M. 2008. Evaluating students'

answerscripts using fuzzy numbers associated with

degrees of confidence. IEEE Transactions on Fuzzy

Systems, 16(2), 403-415.

Weon, S., Kim, J., 2001. Learning achievement evaluation

strategy using fuzzy membership function.

Proceedings of the 31

ASEE/IEEE Frontiers in

Education Conference, Reno: NV.

Wilson, E., Karr, C.L., Freeman, L.M., 1998. Flexible,

adaptive, automatic fuzzy-based grade assigning

system. Proceedings of the North American Fuzzy

Information Processing Society Conference, 334-338.

Wu, D., 2013. Approaches for reducing the computational

cost of interval type-2 fuzzy logic systems: overview

and comparisons. IEEE Transactions on Fuzzy

Systems, 21(1), 80-99.

Zadeh L.A., 1975. The concept of a Linguistic Variable

and Its Application to Approximate Reasoning-I.

Information Sciences, 8, 199-249.

Zadeh, L.A., 1965. Fuzzy sets. Information and Control,

8, 338-353.

Zadeh, L.A., 2005. Towards a generalized theory of

uncertainity (GTU) – an outline. Information Sciences,

172, 1–40.

Zhao, J., Bose, B.K., 2002. Evaluation of membership

functions for fuzzy logic controlled induction motor

drive. In: Proceedings of the 28

Annual Conference

of the Industrial Electronics Society, IEEE (IECON

02), 1, 229-234.

CSEDU 2016 - 8th International Conference on Computer Supported Education