Choquet Integral based Feature Selection for Early Breast Cancer

Diagnosis from MRIs

Soumaya Trabelsi Ben Ameur

1,2

, Florence Cloppet

, Dorra Sellami Masmoudi

and Laurent Wendling

Intelligent System of Perception Group, LIPADE Lab, Paris Descartes University, 45 Saint Pères Street, Paris, France

Computor Imaging and Electronic Systems Group (CIEL), National Engineering School of Sfax (ENIS), Sfax, Tunisia

Keywords: Breast Cancer, Computer Aided Diagnosis, Mammography, Ultrasound, MRI, Dual-energy Contrast-

Enhanced Digital Mammography, Choquet Integral.

Abstract: This paper focuses on breast cancer of the mammary gland. Both basic segmentation steps and usual features

are recalled. Then textural and morphological information are combined to improve the overall performance

of breast MRI in a computer-aided system. A model of selection based on Choquet integral is provided. Such

model is suitable when handling with a weak amount of data even ambiguous in some extent. Achieved results

compared to well-known classification methods show the interest of our approach.

1 INTRODUCTION

Breast cancer is a malignant tumor of the mammary

gland due to the presence of abnormal cells in the

breast tissue. In order to reduce the risk of mortality

and have an adequate treatment, the doctor can make

several different screenings: mammography,

ultrasound, breast MRI, Dual-Energy Contrast-

Enhanced Digital Mammography DECEDM and

other additional detection exams. Therefore they are

faced with a problem of melting and data decision.

Radiologists tend to describe a mass according to its

shape, outline, optical density, etc. The diagnosis of

breast mass is a difficult task, even for an expert

radiologist, because its morphological aspects can be

very subtle and hard to diagnose visually. Therefore,

Computer-Aided Diagnosis (CAD) has been

proposed to support radiologists in the discrimination

of malignant and benign lesion. These approaches are

usually based on three steps: segmentation of the

mass, extraction of characteristics and classification

into malignant and benign. Features extracted from

breast images are classified into texture features,

shape descriptors and kinetic features. There are

attributes that are not necessarily relevant for taking

the decision, and they can induce an error in the

classification thus a multi-criteria selection is

necessary. Choquet integral aims at providing a

robust decision model even with a small training

database (which is the case of our study). This method

allows to select and classify the most significant and

pertinent attributes.

2 DETECTION AND ANALYSIS

SYSTEM

Breast pathologies are classified into two types:

microcalcifications and breast masses. In our study

we are interested to the detection of breast masses.

Breast masses are found in several shots. they are

generally characterized by their shape and contour.

Round or oval masses with well-defined limits are

rather benign lesions. While lobulated and undefined

limits masses are malignant. Breast density

characterizes the heterogeneity of the breast tissue, it

has a link with breast cancer because it has an impact

on the reliability of the interpretation of medical

images. Medical imaging has a crucial role in

reducing breast cancer mortality, by making possible

early detection through screening. Several breast

imaging exists such as mammography, ultrasound,

breast MRI and DECEDM, etc.

Ameur, S., Cloppet, F., Masmoudi, D. and Wendling, L.

Choquet Integral based Feature Selection for Early Breast Cancer Diagnosis from MRIs.

DOI: 10.5220/0005754703510358

In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 351-358

ISBN: 978-989-758-173-1

351

2.1 Mammography

As the primary imaging modality for early detection

and diagnosis of breast cancer, mammography has

achieved significant success. A mammography is a

breast radiography which allows to obtain images of

breast tissue using X-rays to detect anomalies. Radio-

opaque areas are clear and correspond to the fibro-

glandular tissue and calcium. A mammogram is

performed either for breast cancer screening or to

diagnose the presence of symptoms. Mammography

is accessible and non-traumatic, it allows a well

visualizing of microcalcifications. However, the

superposition of different breast tissues limits breast

exploration, a high breast density can be the cause of

an analytical problem and small tumors could be

undetected.

2.2 Ultrasound

The ultrasound breast examination is conventionally

used in addition to mammography, for a differential

diagnosis for cystic lesion/solid lesion and to explore

palpable breast lesions without mammography

translation. It can be a first-line examination of young

women (significant breast density), pregnant women

and patients with breast inflammation. Ultrasound is

a quick and easy exam even in case of dense breast

but exploration of greasy breast is hard. The principal

limits of this modality are its non-reproducibility and

its sensitivity to motion.

2.3 Breast MRI

Breast Magnetic Resonance Imaging is a second line

examination, which comes after mammography and

often after ultrasound, first for high-risk women

because they had many antecedents of cancers in the

family, or that they inherited an abnormal gene

family. It has also been used to elucidate problems of

diagnosis that have not been resolved after the

mammogram and ultrasound. The injection of

contrast agent might be necessary to visualize areas

difficult to explore. The interpretation of breast MRI

is based on the perception of the contrast

enhancement that varies according to the type of

lesion. A quantitative analysis is used to divide the

curve, according to the initial peak, into two parts: the

initial enhancement and the delayed phase. The initial

enhancement can be slow (for benign lesion),

medium (intermediate) or fast (suggestive of

malignancy). In delayed phase, three types of contrast

enhancement are possible: persistent (Benin), tray

(intermediate) and washout (malignant). Breast MRI

is non-invasive and non-irradiating technique, it

allows to study the tumor vasculature independently

of breast density. But it is expensive, it has a limited

availability, a low specificity and doesn’t visualize

microcalcifications very well.

2.4 Dual-energy Contrast-Enhanced

Digital Mammography DECEDM

Dual energy contrast enhanced digital mammography

DECEDM is a promising new modality that combines

mammography and contrast agent injection (iodine).

It aims to acquire, in addition to the usual

morphological information, data about breast

vascularization. DECEDM has a quick and easy

image access and analysis and gives a better

appreciation of tumor spread in the case of an

architectural disorganization the mammography. On

the other side, it doesn’t detect weak vascularized

tumors, an enhancement matrix increases the number

of false positives and the fuzzy kinetics increases

false negatives.

The complementarity between these different

modalities gave us the idea to extract features from

more than one modality to have a better recognition

and description of the tumor. Because of the non-

reproducibility of ultrasound and the fact that

information given by mammography could be found

on DECEDM (in addition to tumor vascularization),

we choose to apply our detection and diagnosis

system to two modalities: breast MRI and DECEDM.

In this paper we will focus on results obtained from

MRIs.

3 SEGMENTATION AND

FEATURE EXTRACTION

Segmentation is a very important stage in breast

cancer diagnostic process. It consists of extracting the

pathological area in the image. A good segmentation

generates an accurate description of the

characteristics of breast pathology. Currently, there

are several image processing methods for the

segmentation of breast lesions, someone’s allow both

detection and segmentation. Liney et al. (Liney,

2006) used region growing algorithm for the

segmentation of breast MRI. Wang et al. (Wang,

2014) applied region growing algorithm to segment

masses in breast MRI detected from a color map.

Although region growing was recommended and

frequently used for image segmentation, it has a

serious limitation. In fact, the growth phase requires

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

352

a criterion of homogeneity. If the seeds are located in

a non-homogeneous area, which is the case with

malignant lesions, the similarity measure will

generate variations which cause the interruption of

the growth process. At first, Chen et al. (Chen, 2004)

also recommended the use of region growing for

segmentation of mammary masses, but then they

offered another method of segmentation based on

fuzzy C-means clustering (FCM) algorithm and

confirmed that the FCM algorithm outperforms the

region growing algorithm (Chen, 2006). However,

conventional FCM clustering does not integrate

information about spatial context which makes it

sensitive to noise and imaging artifacts. Conventional

smoothing filters can be used to compensate this

drawback but they can cause a loss of important

image details, especially image boundaries. Some

approaches (Zhang, 2003), (Li, 2003) proposed to

increase the robustness of FCM to noise but they

show considerable computational complexity. Li et

al. (Li, 2008) propose an active contour based region

model, called the level set method, to segment images

with inhomogeneous intensities or objects with

hidden or undefined contour. Since its first

application for segmentation based contour in early

90s, level set method becomes increasingly popular

for image segmentation. Specially, the level set based

region allows to partition the image into coherent

color, texture and dynamic texture areas. A

comparative study between the snake method and the

level set method led by Winzenrieth et al.

(Winzenrieth, 2003) on hip MRI, proves that the level

sets is most appropriate since it is the more

reproducible, more accurate and require less manual

intervention. To deal with image intensity

inhomogeneity, Li et al. (Li, 2011) proposed a novel

level set region-based method for image

segmentation by deriving a local intensity clustering

property from a model of images with intensity

inhomogeneities and defining a local clustering

criterion function for the intensities in a neighborhood

of each point. Li et al. used their model for

segmentation and bias correction of magnetic

resonance images (MRIs) with promising results.

According to this study, previous results and our

case of study, we choose the level set method to

segment breast mass.

3.1 Level Set Method

The level set method is a generic numerical method

for evolving fronts in an implicit form. The image

segmentation problem can be formulated and solved

with the level set method principally based on well-

established mathematical theories, including calculus

of variations and partial differential equations (PDE).

Consider a curve/interface Γ in movement in a

region Ω. Γ is the zero level of a function φ of higher

dimension usually called a level set function. The

interface in movement at point x at the instant t is

defined as:

(

)



(,)

(

x,t

)



(1)

With φ is positive inside Ω, negative outside, and

null on Γ. Items of this interface will move towards

normal (gradient φ) with a speed  according to the

following equation:





+.∇φ=0

(2)

In fact, only the normal component of v

account



=.

∇

, With |∇φ| is the euclidean

norm, thus equation (1) becomes:





+



∇φ

(3)

The results of segmentation were validated by two

radiologists. Two examples of both malignant and

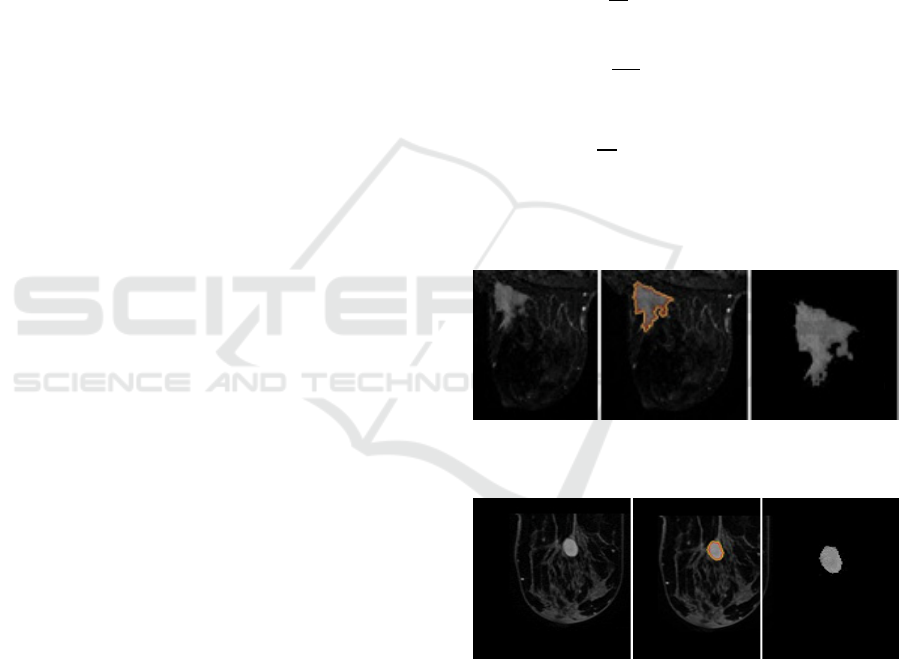
benign lesions are shown in the following figures.

Figure 1: Original MRI, segmented malignant lesion and

lesion extracted respectively from left to right.

Figure 2: Original MRI, segmented benign lesion and lesion

extracted respectively from left to right.

3.2 Feature Extraction

Three kinds of characteristics could be extracted from

the segmented tumors (from MRI and DECEDM):

textures features, shape characteristics and kinetic

features. In this paper, 20 GLCM features and 4 shape

features are extracted and defined as follows.

Choquet Integral based Feature Selection for Early Breast Cancer Diagnosis from MRIs

353

3.2.1 Texture Features

Texture is the result of local variations in brightness

within one small area of an image. A set of Gray

Level Co-occurrence Matrix (GLCM) features, such

as Haralick’s features (Haralick, 1973) (energy,

entropy, correlation, inverse difference moment,

inertia, cluster shade, cluster prominence, etc.) and

other texture characteristics (dissimilarity, maximum

probability, autocorrelation, inverse difference

normalized INN, inverse difference moment

normalized IDN) (Clausi, 2002), (Soh, 1999) are

extracted from the co-occurrence matrix. GLCM

represents how different combinations of pixel

brightness values occur in an image, it depicts the

joint frequencies of all pairwise combinations of gray

levels i and j separated by a distance along a direction

θ (Karthikeyan, 2014). The GLCM is normalized by

the sum of all its elements to calculate the co-

occurrence relative frequency between gray level i

and j. Each entry in GLCM matrix is considered to be

the probability that a pixel with value i will be found

adjacent to a pixel of value j as defined below

(Albregtsen, 2008):





(

1,1

)



(

1,2

)

…

(

1,

)



(

2,1

)



(

2,2

)

…

(

2,

)

…



(

,1

)



(

,2

)

…(,)



3.2.2 Shape Features

A round mass with smooth and well-defined contour

tends to be benign, whereas an irregular or speculated

mass with undefined border tends to be malignant.

Various shape descriptors exist in the literature, and

they are categorized into two groups: contour-based

shape descriptors (Fourier descriptor, wavelet

descriptors, shape signatures, etc.) and region-based

shape descriptors (geometric moments, Zernike

moments, etc.). Four categories of shape descriptors

including compactness, signature, Zernike moments

and GFD were used to diagnose the lesions.

Compactness

Compactness is defined as the ratio of the square of

surface area to the total volume of the lesion. It is used

to quantify the connectedness of the portions in a

lesion. A highly none convex lesion (malignant

lesion) will have a high compactness index, however

benign lesions have a low compactness values (Nie,

2008). Mathematical expression of compactness is as

follows:

compactness=

4π.area

perimeter



(4)

Shape Signature

The shape signature is expressed by the distance of

boundary points from the centroid (xc,yc) of the

shape.

(

)



(

)

−x



)



(

)

−



)



(5)

Where x(n) and y(n) are the coordinates of the

pixels that make the shape boundary, andx







∑

x(k)



, y







∑

y(k)



The signature is normalized by the maximum

distance between the centroid and the k boundary

points to be invariant to rotation and scale,





(



)

()





()

Zernike moments

Zernike moments have been utilized as object

descriptors in several pattern recognition problems

(Hwang, 2006), in edge detection (Li, 2010) and

image retrieval applications (Li, 2009) with

significant results. The Zernike moments are a set of

descriptors obtained using complex kernel functions

based on Zernike polynomials orthogonal to each

other which helps to represent the properties of an

image with no redundancy or overlap of information

between the moments (Tahmasbi, 2011). Zernike

moments of order n with repetition m are defined as:









(ρ,

)











∗

(

ρ,

)

ρdρd

(6)

Where f(x,y) represents the mass shape and V

∗

the complex conjugate of function V. defined as:

,

(

ρ,θ

)



(

)



≤1,j=

√

−1,

where R



(

)

∑

c(n,m,s)ρ



(||)/



and

c(n,m,s)=

(



)

!



(















(













, nand m are

respectively the order and the repetition.

To compute Zernike moments from a digital

image, the integral should be replaced by summations

and the coordinates of the image must be normalized

into [0, 1] by a mapping transform. The discrete form

of the Zernike moments of an image size N × N is

expressed as follows:



n+1





(

)









ρ



e









(7)

Where0≤



≤1, and 



is a normalization

factor.The transformed distance 



and the phase

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

354





at the pixel of (x, y) are given by:ρ





()



()





, θ



=tan









.

Generic Fourier Descriptors

The GFD is extracted from spectral domain by

applying 2-D Fourier transform on polar raster

sampled shape image. It has no redundant features

and allows multi-resolution feature analysis in both

radial and angular directions (Zhang, 2002).

The GFD are based on the Polar Fourier defined

as:

(

ρ,

)

∑∑

(

)





(,)



(,)









(8)

Where r(x,y) and v(x,y) are respectively the radius

and angle of the polar coordinates of the point (x,y), I

is the intensity function and the parameters ρ and θ

are bounded: 0≤ρ<R and 0≤θ<T, with R and T

respectively the radial and the angular resolutions.

Finally, the GFD is written:

GFD

(

m,n

)

=

(,)





(,)

(,)

…

(,)

(,)



(9)

Where m and n are the radial and angular

frequencies and 



is the 1

order moment.

3.2.3 Kinetic Features

Kinetic features are extracted from the Time Intensity

Curve (TIC) of the segmented lesion. As we have

mentioned previously, time intensity curve allows to

divide lesions into malignant and benign according to

their time to peak, an initial rise of signal intensity

within 90 seconds >90% is defined as rapid

enhancement, which is highly suggestive of

malignancy. Four kinetic features could be extracted

from the Characteristic Kinetic Curve CKC

(Maximum enhancement, Time to peak, Uptake rate

and Washout rate) (Chen, 2006).

4 FEATURE SELECTION AND

CLASSIFICATION

4.1 Context of the Study

Pattern recognition methods are generally built

independently. Their combination may lead to

positive correlations, because they aim at achieving

the same goal and are based on the same learning

data. Many classifier combination systems have been

proposed and compared in the literature, and a full

presentation of most of these can be found in a

reference book by Duda et al. (Duda, 2012).

Over the years many aggregation operators have

been introduced. For most of these operators, the

relative importance of a criterion, associated here to a

feature, is represented in the final decision by a

weight assigned to it. By assigning a weight not only

to each participant of the aggregation, but also to each

subset of participants, the operators based on the

Choquet integral are able to capture this synergy in

the associated Fuzzy measure (or capacity). Choquet

integral allows to consider effectively the interactions

between decision rules while providing a model of

robust decision in the presence of little training data

that can be even very inconsistent (Grabisch, 1996).

4.2 Choquet Integral

Let us consider m classes C

… C

and n decision

rules (DRs) X = {D

… Dn}. As in Wendling and al.,

(Wendling, 2008) a decision rule (i.e criterion) is

assumed to be a feature with associated metric. To

classify a new pattern x, we need firstly for each

decision rule j and each class i, to compute a

confidence degree Φ





. Then we combine all these

partial confidence degrees into a global confidence

degree given by Φ

(







)

=Η(Φ





,…,Φ





). Finally, x

is assigned to the class for which the confidence

degree is the highest.

Calculating Choquet integral requires the

definition of a capacity or a fuzzy measure. Let us

denote P as the power set of X, i.e the set of all subsets

of X. Capacity or a fuzzy measure on X, is a function

μ: P(X) → [0, 1] which verifies : μ(∅) = 0, μ(X) = 1

and μ(A)≤ μ(B) if A ⊆ B (monotony).

The Choquet Integral of ϕ





= [ϕ



... ϕ



]

noted

(ϕ





), is defined as :



ϕ





=ϕ

()

μA

(



)

−μA

(



)









(10)

Where 

(



)

(



)

,…()



represents [j…n]

associated criteria in increasing order and A(n+1)=∅.

For a thorough description of the Choquet

integral, the reader may refer to (Grabisch, 1996).

4.3 Learning Step

The calculation of the Choquet integral requires the

assessment of any set of P(X). The main problem is

giving a value to the sets that have more than three

elements while keeping the monotonic property of the

integral. Generally the problem is translated to

another minimization problem, which is usually

Choquet Integral based Feature Selection for Early Breast Cancer Diagnosis from MRIs

355

solved using the Lemke method. M. Grabisch

(Grabisch, 1996) has shown that such an approach

may be inconsistent when using a small number of

samples and has proposed an optimal approach based

on a gradient algorithm. In the approach it is assumed

that in the absence of any information, the most

reasonable way of aggregation is the arithmetic mean.

This algorithm tries to minimize the mean square

error between the values of the Choquet integral and

the expected values.

4.4 Extraction Step

Once the fuzzy measure is learned, it is possible to

interpret the contribution of each decision criterion in

the final decision. We adapt here the strategy

proposed in (Mazaud, 2007) to our breast cancer

diagnosis problem. Several indices can be extracted

from the fuzzy measure, helping to analyze the

behavior of decision criteria. The importance of each

criterion is based on the definition proposed by

Shapley in the game theory (Shapley, 1953). Let us

consider a fuzzy measure μ and a decision criterion



(

,



)























(

∪



)

⊆\



−

(



)

(11)

A decision criterion with an importance index

value less that 1/n can be interpreted as having a low

impact in the final decision. Otherwise an importance

index greater than 1/n describes an attribute more

important than the average. The interaction index,

also called the Murofushi and Soneda index

(Murofushi, 1991), (Murofushi, 1993) represents the

positive or negative degree of interaction between

two decision criteria. If the fuzzy measure is non-

additive, then some criteria interact. The marginal

interaction between D

and D

, conditioned to the

presence of elements of combination T ⊆ X\D

given by:

(∆









)

(



)

=∪







+

(



)

−

(

−





)

−−





(12)

After averaging it over all the subsets of T ⊆

X\D

the assessment of the interaction index of D

and D

, is defined by:

,









= 

(

−−2

)

!!

(

−1

)

(∆









)()

⊆\







(13)

We propose to sort the decision criteria with

increasing order, by considering the values they

reach, using a linear combination of importance and

interaction indexes 





Let us first consider the global impact of

interactions of order 2, or the normalization factor K,

as follows:

=2×  |,







|

,,

(14)

If K is close to 0 (K≈0), then no (or few)

interactions exist between the decision criteria, as

they are independent. The Choquet integral relies on

a weighted sum and the impact of each decision

criterion can be directly assessed by taking its

Shapley values: 









(

,



)

Otherwise, the assessment is performed using the

importance and interaction indices. It is calculated by

integrating the interaction impact of D

relatively to

the minimum of global interaction reached by one

decision criterion, noted M, as follows:







=×(



)×

∑

(

,





)−

/

(15)

=

∑

(







)

,



,

(16)

The decision criterion having the least influence

on the final decision, and interacting the least with the

other criteria is assumed to blur the final decision.

5 EXPERIMENTAL RESULTS

AND DISCUSSION

5.1 Database

A breast MRI database, whose examinations date

from 2014 and 2015, is used in this study. The images

are provided by the hospital Georges Pompidou

radiology department. An expert radiologist

identified the corresponding physical lesions based

on visual criterion and biopsy-proven reports. The

MRI database consists of 58 mass lesion in 40

patients of which 14 lesions are benign and 44 lesions

are malignant. Know that, by virtue of having MRI

performed as part of the clinical exam, these lesions

could be assumed to be difficult to interpret. The

segmentation of breast images was validated by two

experts.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

356

5.2 Results

It is important to note that only subset of features

among the set of features presented before are

relevant despite they were usually used in the

literature. Most of them are based on same

mathematical process and are redundant and blurred

the results. The aim of the approach is to

automatically extract a subset of pertinent features

adapted to the studied application. Each feature is

assumed to be a decision rule. That is descriptor and

associated metric to be consistent with the proposed

methodology. Leave-one-out is performed as few

data are processed and to provided non-biased results.

For a lack of clarity we will study the subset of nine

remaining features providing a score of 100% after

selecting step (that is Energy, Entropy, Homogeneity,

Correlation, Contrast, Cluster Prominence, Cluster

Shade, Compactness, and Zernike moments). The

analyze of Choquet lattice allows to attribute to each

feature a score based on its importance index

(Shapley index) and its global interaction impact. At

each epoch the weakest feature is removed and the

new rate of correct classification is calculated.

The following table shows the variation of correct

classification rates (CCR) by running several

methods.

Table 1: Correct classification rates (CCR) obtained on

subsets of features using well-known classifiers.

Methods

/Removed

feature

Kmeans Knn ANN SVM Choquet

Energy

Entropy

ClusterP

ClusterS

Homog

Contrast

Zernike

100

F= number of used features. Kmeans = K-means clustering.

Knn = k-nearest neighbor. ANN = artificial neural network.

SVM= support vector machine. Choquet = Choquet

integral. ClusterP = cluster prominence. ClusterS = cluster

shade. Homog = homogeinity.

Kmeans and SVM classifiers have a better correct

classification rate CCR (81% and 84% respectively)

with 8 features by removing energy, Knn gives a

better recognition rate (92%) with only 3 features

kept (Zernike, compactness and correlation). Knn,

SVM and Choquet integral provide a better CCR

(81%, 84 and 96% respectively) with two removed

features, energy and entropy, but Choquet integral out

performs all the classification methods with 96% of

CCR. These results attest the good behavior of our

method based on Choquet integral. Furthermore the

importance of the feature can be assessed at each level

(Table 2) as well as their interaction (Table 3).

Table 2: An example of the assessment of the importance

of decision rules (Shapley) associated to a set of 7 features

(table 1).

Shapley F1 F2 F3 F4 F5 F6 F7

values

0.76

1.01 1.09

0.78 0.74

1.46 1.15

Table 3: An example of the assessment of the positive and

negative interactions between decision rules (second order)

associated to a set of 7 features (table 1). Obviously table is

symmetric.

Int. 2 F1 F2 F3 F4 F5 F6 F7

--- -0.18 -0.11 0.08 0.31 0.26 0.64

-0.18 --- -0.16 0.41 0.01 1.09 -0.34

-0.11 -0.16 --- 0.00 0.42 -0.33 0.18

0.08 0.41 0.00 --- 0.54 -0.12 0.74

0.31 0.01 0.42 0.54 --- 0,02 0.70

0.26 1.09 -0.33 -0.12 0.02 --- -0.93

0.64 -0.34 0.18 0.74 0.70 -0.93 ---

6 CONCLUSIONS

In this study, we combined selected textural and

morphological features to improve the overall

performance of breast MRI in a computer-aided

system. We opted for Choquet integral, which

provides a robust model of decision in the presence of

little training data, to select the most pertinent

features. The results are very encouraging (CCR =

96%), despite using a small data set. Further works

are devoted to the extension of this model to process

with other subsets of features extracted from breast

MRI (kinetic features, risk factor, etc.) and from

DECEDM and to merge a set of features in order to

reach a better tumor recognition and classification

which lead to a better decision. Such a generic system

can be useful for other type of dataset for cancer

recognition.

Choquet Integral based Feature Selection for Early Breast Cancer Diagnosis from MRIs

357

REFERENCES

Albregtsen, F., 2008. Statistical Texture Measures

Computed from Gray Level Co-occurrence Matrices.

Image Processing Laboratory Department of

Informatics University of Oslo.

Chen, W., Giger, ML., Bick, U., 2006. A Fuzzy C-Means

(FCM)-Based Approach for Computerized

Segmentation of Breast Lesions in Dynamic Contrast-

Enhanced MR Images. Academic Radiology. Volume

13, issue 1, pages 63–72.

Chen, W., Giger, ML., Bick, U., 2006. Automatic

identification and classification of characteristic kinetic

curves of breast lesions on DCE-MRI. Med Phys. 33(8),

pages 2878-87.

Chen, W., Giger, ML., Lan, L., et al., 2004. Computerized

interpretation of breast MRI: investigation of

enhancement-variance dynamics. Med Phys. Volume

31, pages 1076–1082.

Clausi, DA., 2002. An analysis of co-occurrence texture

statistics as a function of grey level quantization. Can.

J. Remote Sensing. Volume 28, issue 1, pages 45–62.

Duda, RO., Hart, PE., Stork, DG., 2012. Pattern

classification. John Wiley & Sons.

Grabisch, M., 1996. The application of fuzzy integrals in

multicriteria decision making. Eur. J. Oper. Res.

Volume 89, issue 3, pages 445–456.

Haralick, RM., Shanmuga, K., Dinstein, I., 1973. Textural

features for image classification. IEEE Trans Syst Man

Cybern; Smc3 (6):610–21.

Hwang, S.K., Kim, W.Y., 2006. A novel approach to the

fast computation of Zernike moments. Pattern

Recognition. Volume 39 pages 2065–2076.

Karthikeyan, S., Rengarajan, N., 2014. Performance

analysis of gray level co-occurrence matrix texture

features for glaucoma diagnosis. American Journal of

Applied Sciences. Volume 11, pages 248-257.

Li, C., Kao, CY., Gore, JC., Ding, Z., 2008. Minimization

of region-scalable fitting energy for image

segmentation. IEEE Transactions on Image

Processing. Volume 17, issue 10, pages 1940-1949.

Li, C., Huang, R., Ding, Z., Gatenby, JC., Metaxas, DN.,

Gore, JC., 2011. A level set method for image

segmentation in the presence of intensity

inhomogeneities with application to MRI. IEEE

Transactions on image processing. Volume 20, issue 7.

Li, Sh., Lee, MCh, Pun, Ch.M., 2009. Complex Zernike

moments features for shape based image retrieval.

IEEE Transactions on Systems, Man and Cybernetics,

Part A: Systems and Humans 1. Volume 39, pages 227–

237.

Li, X., Li, L., Lu, H., Chen, D., Liang, Z., 2003.

Inhomogeneity Correction for Magnetic Resonance

Images with Fuzzy C-Mean Algorithm. Proc. SPIE Int.

Soc. Opt. Eng., Volume 5032, pages 995–1005.

Li, X., Song, A., 2010. A new edge detection method using

Gaussian–Zernike moment operator. Proceedings of

the IEEE, 2nd International Asia Conference on

Informatics in Control, Automation and Robotics,

pages 276–279.

Liney, GP., Sreenvias, M., Garcia-Alvarez, R., et al., 2006.

Breast lesion analysis of shape technique: semi-

automated vs. manual morphological description. J

Magnetic Resonance Imaging. Volume 23, pages 493–

498.

Mazaud C., Rendek J., Bombardier V., Wendling L., "A

feature selection method based on Choquet Integral and

Typicality Analysis", IEEE International Conference

on Fuzzy Systems, London (UK), 6p, 2007.

Murofushi, T., Sugeno, M., 1991. A theory of fuzzy

measures: Representations, the Choquet integral, and

null sets. J. Math. Anal. Appl. Volume 159, issue 2,

pages 532–549.

Murofushi, T., Soneda, S., 1993. Techniques for reading

fuzzy measures (iii): Interaction index. Proc. 9th Fuzzy

Syst. Symp., Sapporo, Japan. Pages 693–696.

Nie, K., 2008. Quantitative Analysis of Lesion Morphology

and Texture Features for Diagnostic Prediction in

Breast MRI. Academic Radiology, volume 15, issue 12,

pages 1513–1525.

Shapley, L., 1953. A value for n-person games. In

Contributions to the Theory of Games, Annals of

Mathematics Studies, H. Khun and A. Tucker, Eds.

Princeton, NJ: Princeton Univ. Press, pages 307–317.

Soh, LK., Tsatsoulis, C., 1999. Texture analysis of SAR sea

ice imagery using gray level co-occurrence matrices.

IEEE Transactions on Geoscience and Remote Sensing.

Volume 37, issue 2, pages 780–795.

Tahmasbi, A., 2011. Classification of benign and malignant

masses based on Zernike moments. Computers in

Biology and Medicine. Volume 41, pages 726–735.

Wang, TC., Huang, YH., Huang, CS., Chen, JH., Huang,

GY., Chang, YC., Chang, RF., 2014. Computer-aided

diagnosis of breast DCE-MRI using pharmacokinetic

model and 3-D morphology analysis. Magnetic

Resonance Imaging. Volume 32, pages 197-205.

Wendling L., Rendek J., Matsakis P., 2008. Selection of

suitable set of decision rules using Choquet integral,

Statistic Pattern Recognition, S+SSPR'08, pp10.

Winzenrieth, R., Claude, I., Hobatho, MC., Pouletaut, P.,

Sebag, G., 2003. Comparaison de deux méthodes de

segmentation par contours actifs : les snakes et les level

sets pour la segmentation d’IRM de hanche.

Zhang, D., Lu, G., 2002. Generic Fourier descriptor for

shape-based image retrieval. Multimedia and Expo,

ICME '02. Proceedings. IEEE International

Conference. Volume1, pages 425-428.

Zhang, DQ., Chen, S., Pan, ZS., Tan, KR., 2003. Kernel

based fuzzy clustering incorporating spatial constraints

for image segmentation. IEEE International conference

on Machine Learning and Cybernetics. Volume 4,

pages 2189-2192.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

358