Wind Farm Layout Design using Cuckoo Search Algorithm

Shafiqur Rehman

, Syed S. Ali

and Syed H. Adil

Research Institute, King Fahd University of Petroleum & Minerals, Dhahran 31261, Saudi Arabia

Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh 31750, Malaysia

Faculty of Engineering, Sciences, and Technology, Iqra University, Karachi, Pakistan

Keywords: Wind Farm Layout Design, Wind Energy, Optimization, Cuckoo Search Algorithm, Genetic Algorithm.

Abstract: Wind energy has emerged as a strong alternative to fossil fuels for power generation. To generate this

energy, wind turbines are placed in a wind farm. The extraction of maximum energy from these wind farms

demands an efficient layout of the wind farms. This layout determines the location of each turbine in the

wind farm. Due to its sheer complexity, the wind farm layout design problem is considered a complex

optimization problem. In recent years, several attempts have been made to develop techniques and

algorithms for optimization of wind farms. This paper proposes yet another optimization algorithm based on

the cuckoo search (CS), which is a recent optimization method. The proposed cuckoo search algorithm is

compared with genetic algorithm which is by far the highest utilized algorithm for wind farm layout design.

Empirical results indicate that the proposed cuckoo search algorithm outperformed the genetic algorithm for

the given test scenarios in terms of yearly power output and efficiency.

1 INTRODUCTION

Wind power is emerging as an effective source of

cleaner and affordable energy compared to

traditional fossil fuels. These features of wind

energy advocate its use at a massive level, thus

prompting the researchers and energy producers to

give serious attention to wind power generation

during the past many years. This has resulted in

notable developments in various areas of

investigation related to wind energy. These areas

include sensors and instrumentation, assessment of

wind energy potential, design and characterization of

wind turbines, and the development of wind farms

(Ettoumi, 2008) and (Muskaterov and Borissova,

2010). This paper deals with efficient design of wind

farms. More specifically, the aim is optimal

placement of wind turbines in a wind farm, while

considering various design objectives and

constraints.

Although there are various commercially

available software packages for wind farm layout

design, many researchers have developed interest in

utilizing computational intelligence techniques for

the purpose. It is due to the fact that, despite their

sophistication, these software packages merely serve

as assistant to human designers, and the

responsibility of an efficient design mainly lies on

the experience and intelligence of the designer. This

may lead to less efficient designs. On the other hand,

computational intelligence techniques have been

very effectual for a huge variety of complex

optimization problems, since these techniques are

least dependent on human intervention and are

capable of generating efficient solutions due to their

built-in intelligence.

For many years, computational intelligence

algorithms have been used for optimal design of

wind farms, with genetic algorithm (Goldberg,

1989) being the first and the highest utilized

algorithm (Khan and Rehman, 2013) thus far. Many

initial researchers in the domain, such as Mosetti et

al., 1994 and Grady et al., 2005 adapted genetic

algorithm for wind farm design. The algorithm has

also received significant attention by many other

researchers (Khan and Rehman, 2013) for the same

problem. Apart from genetic algorithms, particle

swarm optimization algorithms have also been

utilized for wind farm design (Chwodhury and

Zhang, 2010) (Chowdhury, 2012), (Rahmani et al.

2010) and (Wan et al., 2010). However, application

of other various other intelligent algorithms, such as

ant colony optimization, honey bee colony

optimization, tabu search, and cuckoo search is

Rehman, S., Ali, S. and Adil, S.

Wind Farm Layout Design using Cuckoo Search Algorithm.

In Proceedings of the 5th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2016), pages 257-262

ISBN: 978-989-758-184-7

257

either very limited or non-existent. This paper is,

therefore, motivated by the above observation and

proposes a cuckoo search based algorithm for

efficient wind farm layout design, which will be the

first such attempt to the best of our knowledge.

The rest of the paper is organized as follows. In

Section 2, the wake and cost models used in this

study are described. This is followed by discussion

on the cuckoo search algorithm in Section 3. Section

4 provides the results and discussion, followed a by

a conclusion in Section 5.

2 WAKE AND COST MODELING

The assumptions made in this paper are the same as

proposed in the initial studies (Mosetti et al., 1994)

and (Grady et al., 2005) in the domain. These

assumptions are still in use in recent studies.

Accordingly, a simplified version of Jensen model

(proposed in (Mosetti et al., 1994)) is used in this

paper to find the optimal layout design of a wind

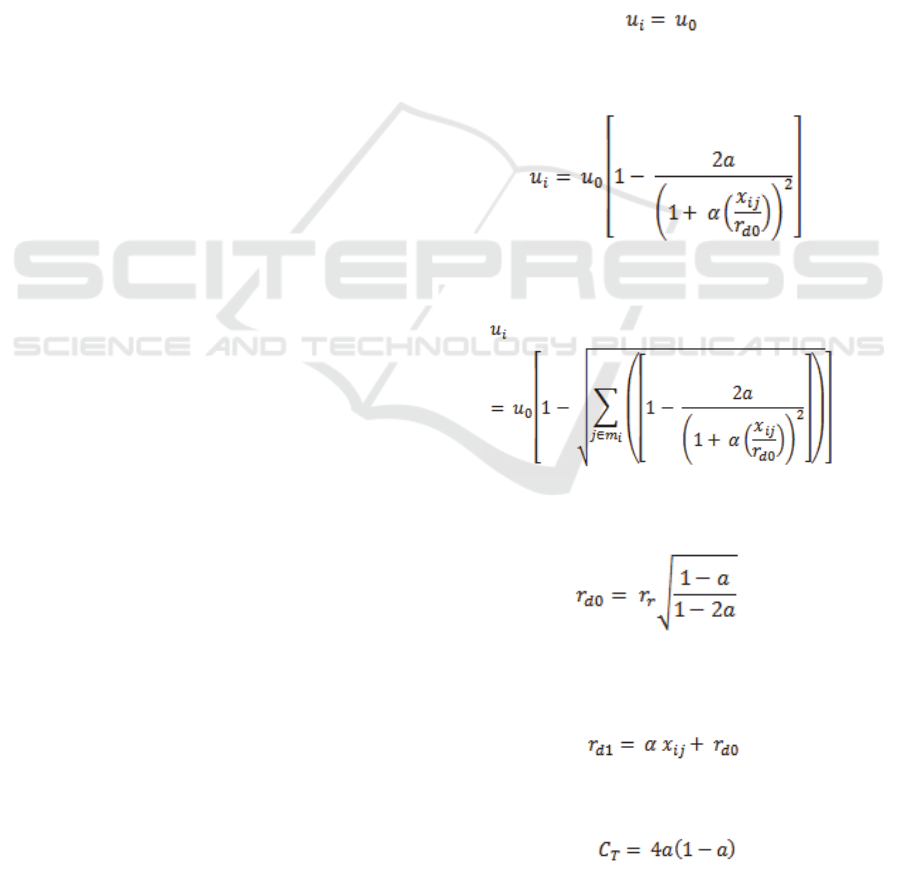
farm. Following notations have been used.

A : Axial induction factor

α : Entrainment factor

: Surface roughness

Z : Hub height

: Thrust coefficient

: Distance downstream from turbine j to

turbine i (i.e., distance between the

current turbine and the turbine creating

wake effect on it)

: Wind speed downstream under multiple

wakes

N : Total number of turbines

: Set of all turbines creating wake effect

on turbine i

: Wake radius immediately downstream of

the wind turbine

Wake radius at x distance downstream of

the wind turbine

Number of rows and columns that exist

in the solution space

The schematic of the wake model is shown in Fig. 1.

Furthermore, Figure 2 illustrates a typical wind farm

grid. For fair comparison of the proposed cuckoo

search algorithm with other techniques, the gird size

and other properties are adopted from the

fundamental studies (Mosetti et al., 1994) and

(Grady et al., 2005). Following these properties, the

grid is divided into 100 possible turbine locations. A

turbine can be placed at the center of a cell. The size

of each cell is taken as five times the rotor diameter

(D). More precisely, since a rotor diameter of 40 m

is assumed, a cell size is 200 m. A hub directly

facing the wind direction is not under effect of any

wake. Therefore, the wind speed remains unaffected

as visible in Figure 2. The equations to calculate the

wake generated power, and optimization objectives

(Eqs. (1) to (12)) have been adopted from Mosetti et

al., 1994 (since the same model was followed by

various other studies) and presented below for the

sake of clarity and completion. Interested reader

may find more details in (Mosetti et al., 1994) on the

wake and power efficiency model. According to this

model, we have

(1)

If the hub is subjected to only one wake, then the

wind speed is affected according to:

(2)

However, if any hub is subjected to multiple wakes,

then the wind speed is determined by

(3)

The radius r

of the wake downstream immediately

after a turbine is calculated using:

(4)

Furthermore, the radius r

of the wake at a distance

downstream of any wind turbine is calculated

using following equation,

(5)

The relationship between thrust coefficient and axial

induction factor is given by

(6)

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

258

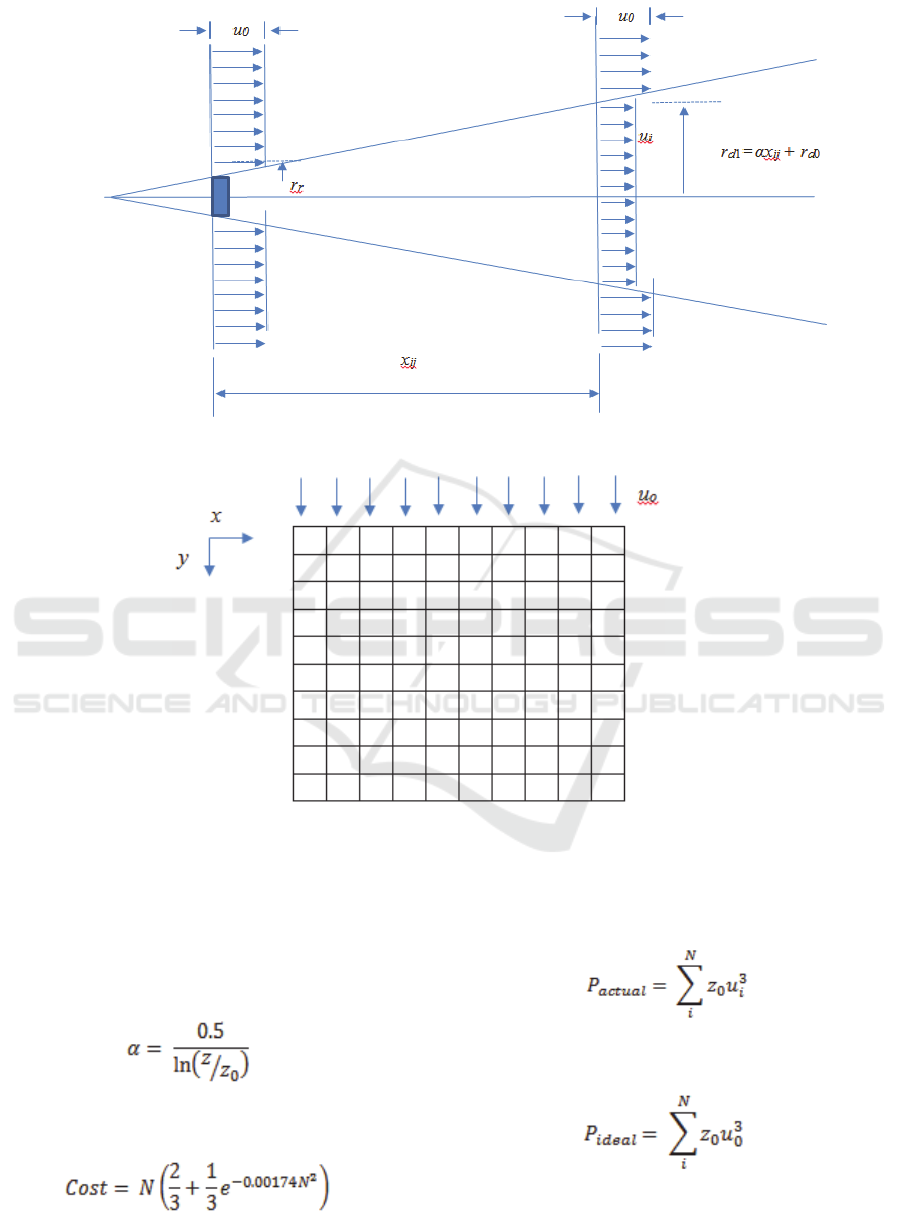
Figure 1: Schematic of the Wake Model.

Figure 2: A 10 x 10 Wind Farm Grid.

The thrust coefficient is normally known for the

system. Therefore, we can calculate axial induction

factor a instead of CT. (The solution of Eq. 6 gives

two values of a. We select one which gives a real

value for r

in Eq. 4). Finally, the entrainment factor

α is found out using the following equation.

(7)

Total cost of placing N turbines in the grid is

calculated using following equation.

(8)

Total power generated by N turbines under

multiples wakes is calculated using following

equation.

(9)

Total power generated by N turbines without any

wake is calculated using following equation.

(10)

The efficiency of the wind power generation is

calculated using following equation.

Wind Farm Layout Design using Cuckoo Search Algorithm

259

(11)

With the above equations, the wind farm layout

design problem is fundamentally the wind turbine

placement problem where the objective is to

minimize the total cost versus total power generated

for N number of turbines. Therefore, the objective of

this optimization problem can be stated as:

(12)

3 CUCKOO SEARCH

ALGORITHM

Cuckoo search is a search algorithm originally

proposed by Yang and Deb in 2009 (Yang and Deb,

2009) as an optimization tool for numerical

functions and continuous problems. The algorithm is

based on the brooding parasitism of cuckoo species

in natural habitat. Some cuckoo species by laying

their eggs in the nests of other host birds (of other

species). Some host birds can engage in direct

conflict with the intruding cuckoos.

The CS algorithm evolves from the following

three behavioral patterns of real cuckoos (Yang and

Deb, 2009):

(1) Each cuckoo lays one egg at a time. The egg

is dumped in a nest randomly chosen by the cuckoo.

(2) The best nests with high quality of eggs

(solutions) will carry over to the next generations.

(3) The number of available host nests is fixed,

and a host can discover an alien egg with probability

∈ (0,1). Thus, the host bird can either throw the

egg out of its nest or abandon the nest in order to

build a completely new nest in a new location.

Each nest represents a potential solution in

search space. The CS algorithm also determines

how to update the position of cuckoo laid egg. Each

cuckoo updates its position of laying egg based on

current step size via Lévy flights. Lévy flight is a

natural phenomenon noticed in some birds and fruit

flies. It is a combination of short and very long

steps, with sudden turns (typically around 90

These sudden turns are of essential importance for

the CS algorithm, and determine the next position of

the bird/fly using the following equation:

(13)

where

> 0 represents a step size. This step size

should be closely related to the scale of the test

function that the algorithm is applied on. In most

cases,

can be set to the value of 1 (Yang and Deb,

2009). It has been shown that the use of Levy flight

is much more efficient in exploring the search space

as its step length is significantly longer when a large

number of steps are performed compared to a simple

random walk. The random step length is drawn from

a Levy distribution which has an infinite variance

with an infinite mean:

,

(14)

The consecutive positions generated through

steps/iterations of a cuckoo, create a random walk

process which obeys a power-law step length

distribution with a heavy tail.

4 RESULTS AND DISCUSSION

The performance of the proposed cuckoo search

algorithm was evaluated empirically through

simulations. A software simulator was exclusively

developed in C++ programming language for this

purpose. Thirty independent runs were done for each

test scenario and results were subjected to statistical

testing as per the standard practice. Two test

scenarios were used depicting different wind

conditions and directions. These scenarios have been

used in several earlier studies (Mosetti et al., 1994),

(Grady et al., 2005), (Emami and Noghreh, 2010),

(Gonzalez et al., 2010), (Huang, 2007), (Huang,

2009), (Mittal, 2010), (Wang et al., 2009a), and

(Wang et al, 2009b). These scenarios are briefly

discussed below for the sake of completeness. The

proposed CS algorithm was benchmarked with

genetic algorithms. The reason for selecting genetic

algorithm for comparison is that the genetic

algorithm has been used in most studies related to

wind farm layout design (Khan and Rehman, 2013).

4.1 Case A

This scenario assumes the wind is coming from all

the directions with equal probability, while

considering mean wind speed of 12 m/s. For

simplified calculations, wind directions were divided

the in 36 equal intervals with 10 degree difference

(i.e., 0

, 10

, 20

, …, 350

). It is also implicitly

assumed that each turbine in the grid rotates along

with the prevailing wind direction, while it is

installed at the center of the cell in the grid. Thus,

each turbine is facing the prevailing wind direction.

The turbines affected by wake from preceding

turbines will receive downstream wind speeds as per

Eqs. (2) and (3) for single and multiple wakes,

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

260

respectively. It is important to mention that since the

wind directions may be approaching from all

directions, it is required to determine the wake

effects geometrically on the turbines downstream.

Table 1 shows the results for the proposed CS

algorithm and GA, while considering 19 and 39

turbines. The results indicate that CS was able to

achieve better results than GA for both turbine

configurations. For example, the total yearly power

output and the efficiency achieved by CS were

higher than that of GA, for both 19 and 39 turbines.

For GA, the yearly output and efficiency with 19

turbines was 9245 KW and 93.859 %, respectively,

while for CS, the corresponding values were

9385.35 KW and 95.287 %. A similar pattern can be

observed for 39 turbines.

4.2 Case B

In this scenario, wind is coming from all possible

directions with equal probability but with varying

mean wind speeds of 8, 12, and 17 m/s. This case is

similar to Case A except for the wind speeds.

Therefore, as in case A, wind direction was divided

in 36 equal intervals with angle difference of 10

degrees (i.e., 0

, 10

, 20

,…, 350

). Furthermore,

turbine installation and calculations of wake effect

remain similar to case A. The complexity of case B

is intensified by the fact that the probability of

having wind direction may be different for different

mean wind speeds. In particular, previous studies

(Mosetti et al.,1994) and (Grady et al., 2005) have

used the probability distribution shown in Fig. 3,

where it is observed that wind distributions from,

270

to 350

are higher than the remaining angles,

with the peak at around 310

. The same distribution

was used to evaluate the performance of the CS

algorithm and comparison with GA.

Figure 3: Varying wind speeds for different directions

(developed from (Mosetti et al.,1994)).

Table 2 shows a comparison between the proposed

CS algorithm and GA. Two configurations

consisting of 15 and 39 turbines were used in the

analysis. Similar to the results of ase A, CS also

outperformed GA for both 15 and 39 turbines. This

is evident from the yearly output and efficiency

which are higher for CS compared with GA, as

depicted in the table.

5 CONCLUSIONS

This paper presented a novel approach for

optimization of a wind farm layout. A recent

optimization technique, namely, the cuckoo search

algorithm, was engineered to optimize the layout

design. The proposed approach was compared with

the infamous genetic algorithm which has been

Table 1: Comparison of solution features for Case A.

Attribute GA CS GA CS

Fitness Value 0.00174 0.00171 0.00157 0.00151

Total kw/ year 9245 9385.35 17220 17860.73

Efficiency (%) 93.859 95.287 85.174 88.343

No. of turbines 19 19 39 39

Table 2: Comparison of solution features for Case B.

Attribute GA CS GA CS

Fitness Value

0.000994 0.000906 0.000803 0.000779

Total kw/ year

13460 14769.38 32038 34563.01

Efficiency (%)

94.620 97.613 86.619 87.857

No. of turbines

15 15 39 39

Wind Farm Layout Design using Cuckoo Search Algorithm

261

extensively used to solve different variations of the

wind turbine layout design problem in many

previous studies. The resulted revealed that the

proposed cuckoo search algorithm produced higher

yearly energy output and better efficiency for all the

considered test scenarios and different number of

wind turbines. This signifies that the cuckoo search

algorithm was more efficient than genetic algorithm

in traversing the search space, which resulted in

better solutions by cuckoo search.

ACKNOWLEDGEMENTS

This work was supported by Deanship of Research

at King Fahd University of Petroleum & Minerals

under project number IN131012.

REFERENCES

Chowdhury, S. and Zhang, J., 2010 Exploring key factors

influencing optimal farm design using mixed-discrete

particle swarm optimization. In Proceedings of 13th

AIAA/ISSMO multidisciplinary analysis and

optimization conference, 1–16.

Chowdhury S., Zhang, J., Messac, A., and Castillo, L.,

2012. Unrestricted wind farm layout optimization

UWFLO: investigating key factors influencing the

maximum power generation. Renew. Energ. 38, 16–

30.

Emami, A., and Noghreh, P., 2010. New approach on

optimization in placement of wind turbines within

wind farm by genetic algorithms. Renew. Energ. 25.

1559-1564.

Ettoumi, F. Y., Adane, A., Benzaoui, M. L., and

Bouzergui, N., 2008. Comparative simulation of wind

park design and siting in Algeria. Renew. Energ. 33,

2333–2338.

Goldberg, D. E., 1989. Genetic Algorithms in Search,

Optimization, and Machine Learning. Addison-Wesley

Publishing Company.

Gonzalez, J., Santos, J., and Payan, M., 2010. Wind farm

optimal design including risk. In Proceedings of IEEE

international symposium modelling electric power

systems, 1–6.

Grady, S., Hussaini, M. , and Abdullah, M., 2005.

Placement of wind turbines using genetic algorithms.

Renew. Energ. 30, 2, 259–270.

Huang, H., 2007. Distributed genetic algorithm for

optimization of wind farm annual profits. In

Proceedings of the IEEE international conference

intelligence system applied to power systems, 1–6.

Huang, H.,2009. Efficient hybrid distributed genetic

algorithms for wind turbine positioning in large wind

farms. In Proceedings of the IEEE international

symposium industrial electronics, 2196–2201.

Khan, S. A., and Rehman, S., 2013. Iterative non-

deterministic algorithms in on-shore wind farm

design: A brief survey. Renew. Sust. Energ. Rev. 19, 3,

370–384.

Mittal, A., 2010. Optimization of the layout of large wind

farms using a genetic algorithm. MS thesis, Case

Western Reserve University.

Mosetti, G., Poloni, C., Diviacco, B.,1994. Optimization

of wind turbine positioning in large wind farms by

means of a genetic algorithm, J. Wind. Eng. Ind. Aero.,

51, 105–116.

Mustakerov, I. and Borissova, D., 2010. Wind turbines

type and number choice using combinatorial

optimization. Renew. Energ. 35, 1887–1894.

Rahmani, R., Khairuddin, A., Cherati, S.M., and Pesaran,

H.A., 2010. A novel method for optimal placing wind

turbines in a wind farm using particle swarm

optimization (PSO). In Proceedings of IEEE

international conference on power engineering, 134–

139.

Wan, C., Wang, J., Yang, G., and Zhang, X., 2010.

Optimal micro-siting of wind farms by particle swarm

optimization. In Proceedings of International

conference on swarm intelligence, LNCS, 198–205.

Wang, F., Liu, D., and Zeng, L., 2009. Modeling and

simulation of optimal wind turbine configurations in

wind farms. In

Proceedings of the IEEE world non-

grid connected wind power energy conference, p. 1–5.

Wang, F., Liu, D., and Zeng, L., 2009. Study on

computational grids in placement of wind turbines

using genetic algorithm. In Proceedings of the IEEE

world non-grid connected wind power energy

conference, 1–4.

Yang, X., and Deb, S., 2009. Cuckoo search via levy

fights. In Proceedings of IEEE Conference on Nature

& Biologically Inspired Computing, 210-214.

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

262