Afﬁne Invariant Self-similarity for Exemplar-based Inpainting

Vadim Fedorov

, Pablo Arias

, Gabriele Facciolo

and Coloma Ballester

Department of Information and Communication Technologies, University Pompeu Fabra, Barcelona, Spain

CMLA, ENS Cachan, Cachan, France

IMAGINE/LIGM,

Ecole Nationale des Ponts et Chauss

ees, Marne-la-Vall

ee, France

Keywords:

Image Inpainting, Self-similarity, Afﬁne Invariance.

Abstract:

This paper presents a new method for exemplar-based image inpainting using transformed patches. We build

upon a recent afﬁne invariant self-similarity measure which automatically transforms patches to compare them

in an appropriate manner. As a consequence, it intrinsically extends the set of available source patches to copy

information from. When comparing two patches, instead of searching for the appropriate patch transforma-

tion in a highly dimensional parameter space, our approach allows us to determine a single transformation

from the texture content in both patches. We incorporate the afﬁne invariant similarity measure in a varia-

tional formulation for inpainting and present an algorithm together with experimental results illustrating this

approach.

1 INTRODUCTION

Image inpainting, also known as image completion or

disocclusion, refers to the recovery of occluded, miss-

ing or corrupted parts of an image in a given region

so that the reconstructed image looks natural. It has

become a key tool for digital photography and movie

post-production where it is used, for example, to elim-

inate unwanted objects that may be unavoidable dur-

ing ﬁlming.

Automatic image inpainting is a challenging task

that has received signiﬁcant attention in recent years

from the image processing, computer vision, and

graphics communities. Remarkable progress has been

achieved with the advent of exemplar-based methods,

which exploit the self-similarity of natural images by

assuming that the missing information can be found

elsewhere outside the inpainting domain. Roughly

speaking, these methods work by copying patches

taken from the known part of the image and pasting

them smartly in the inpainting domain. These meth-

ods can obtain impressive results but many of them

rely on the assumption that the required information

can be copied as it is, without any transformations.

Therefore, applicability of such methods is limited to

the scenes in which objects are in a fronto-parallel po-

sition with respect to the camera.

In the image formation process, textured objects

may appear distorted by a projective transformation

Figure 1: Self-similarity under perspective distortion. The

human brain can easily ﬁll-in missing information behind

the red rectangles in the examples above. We propose a

method able to automatically do the same for distortions

that can be locally approximated by an afﬁnity.

(see Figure 1). This is a pervasive phenomenon in

our daily life. In fact, any person can mentally ﬁll-in

occluded parts of an image, even if the missing in-

formation is available to them under a different per-

spective. Our brain is able to appropriately transform

the available information to match the perspective of

the occluded region. For instance in Figure 1 one can

easily infer what is hidden behind the red rectangle in

the grafﬁti scene on the right, or use the non-trivially

distorted context in the left image to ﬁll-in the hole.

In this work we address this issue by transforming

known patches before pasting them in the inpainting

domain. The transformation is determined for each

patch in a fully automatic way. Moreover, instead

of searching for an appropriate transformation in a

highly dimensional space, our approach allows us to

determine a single transformation from a surrounding

texture content. As opposed to some previous works

Fedorov, V., Arias, P., Facciolo, G. and Ballester, C.

Afﬁne Invariant Self-similarity for Exemplar-based Inpainting.

DOI: 10.5220/0005728100480058

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 50-60

ISBN: 978-989-758-175-5

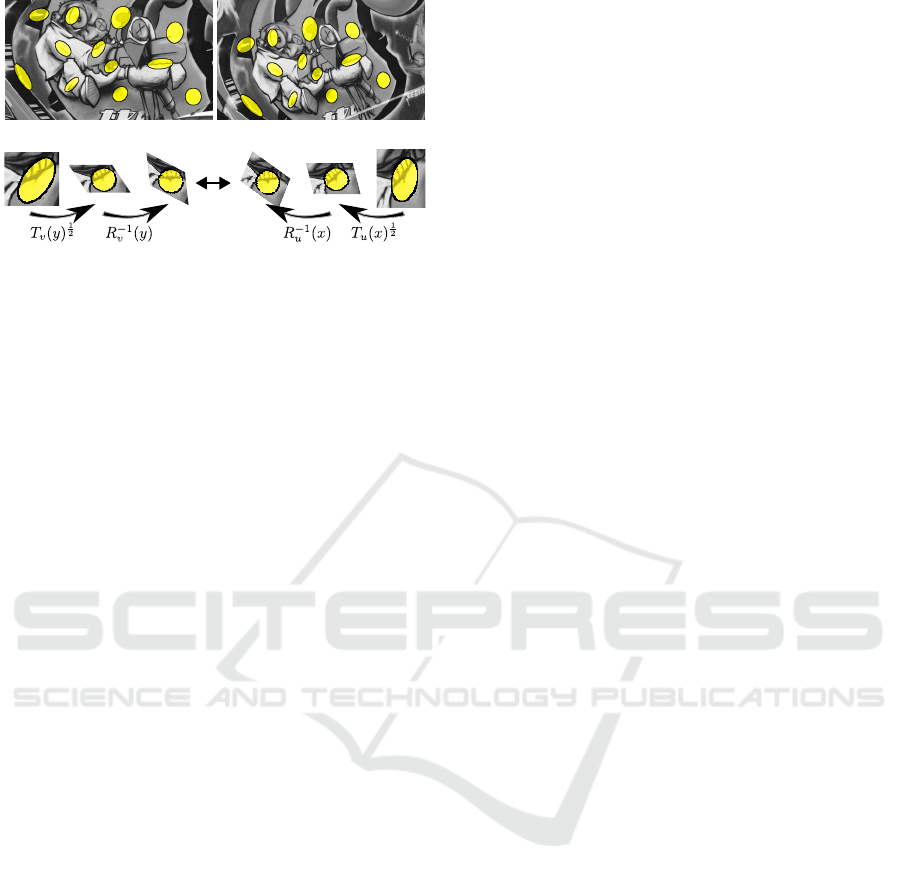
Figure 2: Afﬁne covariant neighborhoods computed at cor-

responding points in two images taken from different view-

points. The neighborhoods are computed with the algorithm

described in Section 3. Note that, despite the change in ap-

pearance, the neighborhoods manage to capture the same

underlying texture. An afﬁne invariant patch comparison is

achieved by normalizing the patches to circles and aligning

them with suitable rotations, as depicted in the diagram at

the bottom.

which only consider rotations and scalings, we can

handle full afﬁnities, which in principle extends the

applicability of the method to any transformation that

can be locally approximated by an afﬁnity, such as

perspective distortion.

We follow the approach recently proposed in (Fe-

dorov et al., 2015), where afﬁne covariant tensor

ﬁelds computed a priori in each image are used to

deﬁne an afﬁne invariant similarity measure between

patches. We incorporate this measure into a varia-

tional inpainting formulation. The afﬁne covariant

tensors determine elliptical patches at each location of

the image domain. Due to the afﬁne covariance prop-

erty of the tensors, these patches transform appropri-

ately when computed on an afﬁnely transformed ver-

sion of the image. Figure 2 illustrates the patches de-

ﬁned by the afﬁne covariant tensors of (Fedorov et al.,

2015), computed for a set of corresponding points

in two images related by a homography. Note that

even though the transformation is not an afﬁnity, the

patches still match, since a homography can be locally

approximated by an afﬁnity.

The paper is organized as follows. Section 2 re-

views the related work. In Section 3, we summarize

the results of (Fedorov et al., 2015) which motivates

the deﬁnition of the similarity measure we use. Sec-

tion 4 is devoted to the inpainting method and algo-

rithm we propose. In Section 5 we present some ex-

periments asserting the validity of our theoretical ap-

proach together with a comparison with well-known

exemplar based methods. Finally, Section 6 con-

cludes the paper.

2 RELATED WORK

Most inpainting methods found in the literature can

be classiﬁed into two groups: geometry- and texture-

oriented depending on how they characterize the re-

dundancy of the image.

The geometry-oriented methods formulate the in-

painting problem as a boundary value problem and the

images are modeled as functions with some degree of

smoothness expressed, for instance, in terms of the

curvature of the level lines (Masnou and Morel, 1998;

Ballester et al., 2001; Masnou, 2002; Chan and Shen,

2001b; Cao et al., 2011), with propagation PDE’s

(Bertalm

ıo et al., 2000), or as the total variation of the

image (Chan and Shen, 2001a). These methods per-

form well in propagating smooth level lines or gradi-

ents, but fail in the presence of texture or big inpaint-

ing domains.

Exemplar-based (also called texture-oriented)

methods were initiated by the work of Efros and Le-

ung (Efros and Leung, 1999) on texture synthesis. In

that work the idea of self-similarity is exploited for di-

rect and non-parametric sampling of the desired tex-

ture. The self-similarity prior is one of the most inﬂu-

ential ideas underlying the recent progress in image

processing and has been effectively used for differ-

ent image processing and computer vision tasks, such

as denoising and other inverse problems (Foi and Bo-

racchi, 2012; Buades et al., 2005; Gilboa and Osher,

2008; Peyr

e, 2009; Pizarro et al., 2010). It has also

found its application to inpainting: the value of each

target pixel x in the inpainting domain can be sampled

from the known part of the image or even from a vast

database of images (Hays and Efros, 2007).

The exemplar-based approach to inpainting has

been intensively studied (Demanet et al., 2003; Cri-

minisi et al., 2004; Wexler et al., 2007; Kawai et al.,

2009; Aujol et al., 2010; Arias et al., 2011). How-

ever, many such methods are based on the assumption

that the information necessary to complete the image

is available elsewhere and can be copied without any

modiﬁcation but a translation.

Some works consider a broader family of transfor-

mations. Drori et al. (Drori et al., 2003) used heuris-

tic criteria to vary the scale of patches. Mansﬁeld et

al. (Mansﬁeld et al., 2011) and Barnes et al. (Barnes

et al., 2010) extended the space of available patches

by testing possible rotations and scales of a source

patch. The search in the space of available patches is

usually performed by a collaborative random search.

However, this implies that for each query patch, the

position of the matching patch as well as the param-

eters of the transformation (scale, rotation angle, tilt,

etc) must be determined. The high dimensionality of

Afﬁne Invariant Self-similarity for Exemplar-based Inpainting

the parameter space makes the search problem very

computationally expensive and the excessive variabil-

ity of candidates may lead to unstable results. In

order to restrict the search space, authors of (Cao

et al., 2011) propose to combine an exemplar-based

approach that includes all rotated patches, with a geo-

metric guide computed by minimizing Euler’s elastica

of contrasted level lines in the inpainted region.

Several authors (Pavi

c et al., 2006; Huang et al.,

2013) have addressed this issue using some user inter-

action to guide the search process. For example, the

user provides information about the symmetries in the

image, or speciﬁes 3D planes which are then used for

rectiﬁcation and the rectiﬁed planes in turn are used

for searching for correspondences. Recently, Huang

et al. (Huang et al., 2014) proposed a method for auto-

matic guidance that searches for appropriately trans-

formed source patches. It starts by detecting planes

and estimating their projection parameters, which are

then used to transform the patches. This allows one

to handle perspective transformations, in situations

when representative planes can be detected.

Most of those works use a similarity measure,

either explicitly or implicitly, to compute a matching

cost between patches. We propose to use an afﬁne

invariant similarity measure which automatically dis-

torts the patches being compared (Fedorov et al.,

2015). Our method considers a rich patch space that

includes all afﬁne-transformed patches, however, for

each pair of patches the transformations are uniquely

determined using the image content. This effectively

limits the search space, making the method more sta-

ble. Since the patch distortions depend on the tex-

ture content of the image, our technique is related in

that sense to a shape-from-texture approach (G

arding,

1992; G

arding and Lindeberg, 1996; Ballester and

Gonzalez, 1998).

Let us remark that this similarity measure applies

to any transformation that can locally be approxi-

mated by an afﬁnity. Moreover, since it has the same

complexity as the usual weighted Euclidean distance

between patches, it is thus well-suited for practical

applications.

In this paper we extend the variational framework

described in (Wexler et al., 2007; Kawai et al., 2009;

Arias et al., 2011) proposing a new energy and an

optimization algorithm for afﬁne invariant exemplar-

based inpainting.

Let us ﬁnally note that (Wang, 2008) proposed

a self-similarity measure for image inpainting, com-

paring dense SIFT descriptors on square patches of a

ﬁxed size. However, the method is not fully afﬁne in-

variant, for example, neither the dense SIFT descrip-

tors nor the square patches are scale invariant. Several

authors have addressed the afﬁne distortion and afﬁne

invariance problem in other contexts such as image

comparison (Mikolajczyk and Schmid, 2004), object

recognition (Matas et al., 2004), and stereo (Garding

and Lindeberg, 1994).

3 AN AFFINE INVARIANT

SIMILARITY MEASURE

Non-local self-similarity is an accepted prior for nat-

ural images. To formalize it, a patch similarity or

comparison measure is needed. Let us consider the

general problem of comparing patches on two images

u : Ω

→ R and v : Ω

→ R, Ω

,Ω

⊆ R

. A widely

used comparison measure between two patches cen-

tered respectively at x and y is the weighted squared

Euclidean distance

D(t,x,y) =

(h)(u(x + h) − v(y + h))

dh, (1)

where g

is a given window that we assume to be

Gaussian of variance t. The Gaussian g

represents

a weighted characteristic function of both patches be-

ing compared and determines the size of the patches

or, in other words, the scale.

In many occasions, similar patches exist in the im-

age but have undergone a transformation, for example

due to a different position with respect to the camera.

The Euclidean distance is not appropriate for detect-

ing these similarities. Consider for example a simple

case in which v is a rotated version of image u. If the

rotation is known, we should use the Euclidean dis-

tance between patches in u and rotated patches in v,

namely

(t,x,y) =

(h)(u(x + h) − v(y + Rh))

dh.

(2)

In a more realistic scenario, one does not know the

appropriate transformation that matches both patches

being compared and even whether it exists. Some

previous works addressed this issue by searching

among all possible transformations (Barnes et al.,

2010; Mansﬁeld et al., 2011) which involves probing

of all the parameters (scale, rotation angle, etc). The

high dimensionality of the parameter space makes the

problem very difﬁcult. In this paper we use an afﬁne

invariant similarity measure, introduced in (Fedorov

et al., 2015), that automatically deduces this transfor-

mation from the local texture context.

The similarity measure deﬁned in (Fedorov et al.,

2015) is based on afﬁne covariant tensor ﬁelds a pri-

ori computed in each image. It was derived as an ap-

proximation to a more general framework introduced

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

in (Ballester et al., 2014), where similarity measures

between images on Riemannian manifolds are stud-

ied.

In the remainder of this section we present an

alternative, self-contained overview of this similar-

ity measure. We ﬁrst brieﬂy discuss the concept of

afﬁne covariant tensors. Then we show how they are

used to deﬁne the afﬁne invariant similarity measure

and establish the relation between our derivation and

the theory of (Ballester et al., 2014; Fedorov et al.,

2015). Finally, we describe an algorithm to compute

the afﬁne convariant tensors.

Afﬁne Covariant Structure Tensors. We consider

an image-dependent tensor ﬁeld T

as a function

that associates a tensor (a symmetric, positive semi-

deﬁnite 2 × 2 matrix) to each point x in the image do-

main. The tensor ﬁeld is said to be afﬁne covariant if

for any afﬁnity A

(x) = A

(Ax)A, (3)

where u

(x) := u(Ax) denotes the afﬁnely trans-

formed version of u. A geometric interpretation of

this property is the following. Given a tensor T

(x)

we can associate to it an elliptical region of “radius”

r centered at x

(x,r) = {y : hT

(x)(y − x), (y − x)i ≤ r

}. (4)

When the tensor is afﬁne covariant, we have that

(x,r) = B

(Ax,r). This implies that the tensors

can be used to deﬁne regions that transform appropri-

ately via an afﬁnity (Figure 2).

The afﬁne covariant tensors at two corresponding

locations allow to extract the afﬁne distortion between

corresponding neighborhoods (or patches), up to a ro-

tation, as shown in (Fedorov et al., 2015). Indeed, for

any afﬁne transformation A, there exists an orthogonal

matrix R such that

A = T

(Ax)

−

(x)

. (5)

This last equation provides an intuitive geometric

relationship between the tensors, the associated ellip-

tical regions and the afﬁnity. Consider a point x and

the corresponding afﬁne covariant elliptic neighbor-

hood B

(x). Mapping B

(x) by the afﬁnity yields

(Ax). The application of A can be decomposed in

three steps. First, applying T

(x)

1/2

, we transform

(x) into a circle or radius r. We refer to the re-

sulting patch as a normalized patch. Then, a rotation

is applied to the normalized patch. Finally, T

(Ax)

−

maps the rotated normalized patch to the elliptical

neighborhood B

(Ax).

To fully determine the afﬁnity A, one needs to ﬁnd

the rotation R. Any rotation would yield an afﬁn-

ity that maps the elliptical neighborhood associated

to T

at x to the one associated to T

at Ax. For

a wrong value of the rotation, the image content in-

side both neighborhoods will not match. Therefore,

the right value for the rotation can be computed by

aligning the image content of both patches. For this

aim, we decompose the rotation as R = R

(y)R

−1

(x),

where R

(y) and R

(x) are estimated from the image

content in the patches. In practice, we calculate them

by aligning the dominant orientation of the normal-

ized patches to the horizontal axis. To compute the

dominant orientation we use histograms of gradient

orientations as in the SIFT descriptors (Lowe, 2004).

An Afﬁne Invariant Patch Similarity. We are in-

terested in comparing the neighborhoods around two

points x, y deﬁned in images u and v. The neighbor-

hoods are deﬁned by the local metric given by the ten-

sors T

(x) and T

(y). In order to compare both neigh-

borhoods, a mapping between them is needed. Eq. (5)

suggest the following deﬁnition:

(x,y) = T

(y)

−

(y)R

−1

(x)T

(x)

. (6)

We can interpret P

(x,y) as an afﬁnity, mapping the

elliptical patch associated to T

(x) into the one asso-

ciated to T

(y). If v is an afﬁnely transformed version

of u, then P(x, y) recovers the true afﬁnity. An afﬁne

invariant patch similarity measure could be built by

computing the distance between the elliptical patch at

y and the result of applying P

(x,y) to the patch at

x. In practice, it is more suitable to transform both

neighborhoods to the circle of radius r (as depicted in

the second line of Figure 2) and compare the aligned

normalized patches:

(t,x,y) =

∆

(h)·



u(x + T

−

(x)h) − v(y + T

−

(y)h)



dh, (7)

where ∆

is a disc centered at the origin with radius

proportional to the scale t and big enough such that

the weighting function g

has effective support in ∆

is an afﬁne invariant patch distance which intrinsi-

cally extends the set of available patches. We will ap-

ply it in Section 4 to exemplar-based inpainting. Let

us also remark that formula (7) has the same complex-

ity of the patch comparison formula (1).

The similarity measure corresponding to (7) was

derived in (Fedorov et al., 2015) as a computationally

tractable approximation of the linear case of the mul-

tiscale similarity measures introduced in (Ballester

et al., 2014). There, the authors show that all scale

spaces of similarity measures D(t, x, y) satisfying a

set of appropriate axioms are solutions of a fam-

ily of degenerate elliptic partial differential equations

Afﬁne Invariant Self-similarity for Exemplar-based Inpainting

(PDE). Images are considered in those papers as Rie-

mannian manifolds endowed with a metric deﬁned by

a tensor ﬁeld. If this tensor ﬁeld is afﬁne covariant,

the resulting similarity measure is afﬁne invariant. In

this Riemannian framework P

deﬁnes an isometry

between the tangent spaces in two manifolds. The au-

thors refer to it as the a priori connection, since it is

related to the notion of connection appearing in paral-

lel transport (see (Ballester et al., 2014) for details).

WKB approximation method, named after

Wentzel, Kramers and Brillouin, was used in (Fe-

dorov et al., 2015) to ﬁnd this approximate solution

to a linear partial differential equation with spa-

tially varying coefﬁcients as a convolution with a

short-time space-varying kernel.

Computation of Afﬁne Covariant Tensors. The

following iterative algorithm introduced in (Fedorov

et al., 2015) allows us to compute a dense ﬁeld of

afﬁne covariant tensors and the associated neighbor-

hoods on an image u

(k)

(x) =

(k−1)

(x,r)

Du(y) ⊗ Du(y)dy

Area(B

(k−1)

(x,r))

, (8)

where B

(k)

is the elliptical region associated to T

given by (4) for k ≥ 2, and B

(0)

(x,r) = {y : |Du(x)(y −

x)| ≤ r} for k = 1.

In this paper we follow the notation of (Fedorov

et al., 2015) and denote by T

(x) the afﬁne covariant

structure tensor T

(k)

(x) for a ﬁxed value of k (k = 30)

and a given value of r (r > 0 is a free parameter which

is in range [250, 350] in our experiments). We denote

by B

(x) the afﬁne covariant neighborhood B

(k)

(x,r).

To simplify notation in the following sections,

we are going to assume that R

= Id and R

= Id.

In order to stress that D

in (7) refers to a patch

distance, we will use interchangeably D

(t,x,y) or

(x), p

(y)), where p

(x) denotes the elliptic

patch centered at x. The patch p

(x) := p

(x,·) is de-

ﬁned by p

(x,h) := u(x +T

(x)

−

h), where h belongs

to a disc centered at 0 ∈ R

. Note that the scale t in

(7) reﬂects the support of the Gaussian g

and, hence,

the size of the patch used for the comparison.

4 INPAINTING FORMULATION

Exemplar-based inpainting methods aim at ﬁlling-in

the image so that each patch in the inpainting domain

is similar to some known patch. This requires com-

paring known patches with partially or completely un-

known patches. For this we extend the variational

framework described in (Wexler et al., 2007; Kawai

et al., 2009; Arias et al., 2011) by using the afﬁne

invariant similarity measure D

given in (7). We for-

mulate the problem of inpainting from afﬁnely trans-

formed patches via the minimization of the following

energy functional

E(u,ϕ) =

(x), p

ˆu

(ϕ(x))) dx, (9)

where O ⊂ Ω ⊂ R

is the inpainting domain, ˆu : Ω \

O → R is the known part of the image,

O includes all

the centers of patches intersecting O (i.e., the centers

of unknown patches) and

is its complement, i.e.

the centers of fully known patches. The minimization

of (9) aims at ﬁnding a visually plausible completion

u of ˆu in the unknown region O. While the additional

variable ϕ :

O →

determines, for each unknown

target patch, the location of a source patch from which

the information will be copied.

This energy compares patches deﬁned on elliptic

domains centered at x and ϕ(x). In the known part

of the image, these domains are deﬁned by the afﬁne

structure tensors T

ˆu

. Since the image is unknown in-

side the inpainting domain we have to estimate the

tensors together with the image. The relationship be-

tween u and T

introduces a complexity in the mini-

mization of (9). Therefore, we propose to relax it and

consider the minimization of the energy

E(u,ϕ,G) =

∆

(h)



u(x + G(x)

−

h) − ˆu(ϕ(x) + T

ˆu

(ϕ(x))

−



dhdx

(10)

where G(x) is an invertible 2 × 2 matrix, ∀x ∈

O. For

now, we will not restrict the tensor ﬁeld G to be given

by the afﬁne structure tensors T

. Instead, we consider

them as an additional variable, in principle indepen-

dent of u. In this way, we do not have to deal with the

complex dependency between T

and u. In practice,

due to the properties of the afﬁne structure tensors, it

turns out that the G can be estimated from T

(x), as

will be explained in the next section.

4.1 Approximate Minimization

Algorithm

We compute a local minimum of the energy with an

alternating optimization scheme on the variables u, G

and ϕ.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

Image Update Step. In the image update step, ϕ

and G are ﬁxed, and the energy is minimized with

respect to u. With the change of variables z = x +

G(x)

−

h, the Euler-Lagrange equation leads to the

following expression:

u(z) =

C(z)

(G(x)

(z − x))

ˆu



ϕ(x) + T

ˆu

(ϕ(x))

−

G(x)

(z − x)



|G(x)

|dx,

(11)

where C(z) is normalization factor such that the sum

is an average. The ﬁeld G determines elliptic patches

centered at each x ∈

O. For each one of these patches

a matching patch centered at ϕ(x) is known, as well

as its shape which is given by tensor T

ˆu

(ϕ(x)). The

corresponding patch is then warped via the afﬁnity

P(x,ϕ(x)) = T

ˆu

(ϕ(x))

−

G(x)

, and aggregated in the

inpainting domain. Note that if G(x) = T

(x), then

P(x,ϕ(x)) coincides with Eq. (6) (recall that for sim-

plicity in the presentation we are assuming that the

rotations in Eq. (6) are the identity).

Afﬁne Correspondence Update Step. Given a

ﬁxed u, the minimization with respect to (ϕ,G) can

be performed by independently minimizing the patch

error function D

for each x ∈

O. This problem is

very complex to solve since it is a nearest neighbor

search where we also optimize for the afﬁne transfor-

mation of the patch at x, given by G.

We will exploit the properties of the afﬁne struc-

ture tensors to estimate an approximate solution. For

that, let us consider a completion candidate u and as-

sume that a local vicinity of x on u is an afﬁnely

transformed version of a local vicinity of ϕ(x) on

ˆu. That is, u(x + h) = ˆu(ϕ(x) + Ah), which is the

case when x and ϕ(x) do actually correspond. Set-

ting G(x) such that T

ˆu

(ϕ(x))

−

(x) = A will lead

to a correct mapping and zero patch distance. On

the other hand, using (6) we can ﬁnd this afﬁnity as

A = T

ˆu

(ϕ(x))

−

(x)

where R is some orthogonal

Algorithm 1: Approximate minimization of

E(u,ϕ, G).

Require: Initial condition u

at O, tolerance τ > 0.

1: repeat

2: Compute afﬁne structure tensors T

k−1

(x) and

rotations R

k−1

(x) for all x ∈

3: Estimate optimal correspondences ϕ

using the

modiﬁed PatchMatch (see Sect 4.2).

4: Update image: u

= argmin

E(u,ϕ

), sub-

ject to u

= ˆu in O

5: until ku

− u

k−1

k < τ.

2×2 matrix and T

is calculated on u. Then G(x) such

that G

(x) = R(x)T

(x), together with ϕ(x), will be

global minimizers of the patch error function D

x. Therefore, we need to search only for ϕ(x) and

R(x). An approximate ϕ(x) can be found efﬁciently

using our modiﬁed version of the PatchMatch algo-

rithm (Barnes et al., 2009), detailed in Section 4.2,

and the additional rotation R(x) can be determined as

described in Section 3. Of course, if the neighbor-

hood of x does not match any afﬁnely transformed

patch, then the estimated G might not minimize the

patch error function D

Another interpretation of the approximate mini-

mization can be given by adding to the minimization

E(u,ϕ,G) the constraint that G

(x) = R(x)T

(x)

for all x ∈

O and for some rotation matrix R(x),

namely,

min

E(u,ϕ,G) subject to G

= R

−1

The correspondence update step corresponds to the

constrained minimization of the energy with respect

to ϕ,G for a ﬁxed image u. In the image update step

the energy is minimized with respect to u, but with-

out enforcing the constraint. Therefore, our approxi-

mate minimization can be seen as an alternating min-

imization applied to a constrained problem. The con-

straint is enforced only when minimizing with one of

the variables (the pair ϕ,G). There are no theoretical

guarantees for the convergence of such a scheme, al-

though we have not yet encountered a practical case

where the algorithm failed to converge.

4.2 Implementation Details

Image Update Step. The actual implementation of

(11) is

u(z) =

C(z)

∑

x∈

(x)(z − x)) m

(x)w(x,ϕ(x))

ˆu



ϕ(x) +

(x,ϕ(x))(z − x)



(x)|, (12)

where

(x,ϕ(x)) = T

−

ˆu

(ϕ(x))RT

(x) is the esti-

mated a priory connection between x and ϕ(x). The

tensor ﬁeld T

is computed using the inpainted image

u from the previous iteration. m

is a conﬁdence mask

that takes values from 1 to 0, decreasing with the dis-

tance to the set of known pixels O

. This mask is

usual in exemplar-based inpainting, e.g. (Arias et al.,

2011), since it helps to guide the ﬂow of information

from the boundary towards the interior of the inpaint-

ing domain, eliminating some local minima and re-

ducing the effect of the initial condition. Finally, let

Afﬁne Invariant Self-similarity for Exemplar-based Inpainting

us comment on the additional weight w(x,ϕ(x)). Usu-

ally, all patches containing a pixel z contribute to its

color value. To control the amount of contributors,

we introduce an auxiliary Gaussian weight w(x, ϕ(x))

that depends on our patch distance D

(t,x,ϕ(x)). It

allows us to cut off contributors with low similarity

(high distance) values, which in turn results in sharper

reconstructions.

The energy (9) is non-convex and has several lo-

cal minimia. As a consequence, there is a dependency

on the initialization. To alleviate this dependency, we

aid the propagation of information from the boundary

towards the interior of the inpainting domain in the

following way. Recall that the extended domain

contains the centers of all ellipses overlapping the in-

painting domain. We dilate

O a few pixels to capture

a narrow band around the inpainting domain of com-

pletely known elliptic patches. Since these patches do

not intersect the inpainting domain, they do not yet

contribute to the inpainting. For these pixels, during

the image update step we extend their neighborhoods

by setting a larger radius value 2r (for this we do

not recompute the tensors, therefore, we only change

the size but not the shape of the associated neighbor-

hood). This results in bigger ellipses, which now may

overlap the domain. This boosts the information prop-

agation at the boundaries of the inpainting domain

during the very ﬁrst iterations of inpainting.

Afﬁne Correspondence Update Step. During the

update of the correspondence map we compute an ap-

proximation of the nearest neighbor ﬁeld using Patch-

Match (Barnes et al., 2009; Barnes et al., 2010). The

PatchMatch algorithm speeds up the computation of

optimal correspondences by exploiting the correla-

tion between patches so that they can be found col-

lectively. Since we are working with elliptic patches

which might be arbitrarily rotated, we adapt the

PatchMatch propagation scheme to take it into ac-

count. Let x be the current pixel and d

= (±1,0),

Figure 3: Propagation directions in the modiﬁed scheme.

= (0, ±1) be the directions of propagation. Then,

the adjacent pixels y

= x −d

(i = 1,2) are tested dur-

ing the propagation. Assume i = 1 (see Figure 3).

Pixel ˆy = ϕ(y) is the current nearest neighbor can-

didate for y. The standard PatchMatch would try to

propagate position ˆy + d to pixel x. In contrast, we

calculate the direction

d =

(y, ˆy)d, where

(·,·) is

the a priori connection, and we try a few positions

along that direction. This generalization gives more

meaningful propagation along edges.

At early iterations of our algorithm, the inpainted

image may be blurry. It comes from inconsistency

between color values proposed for ﬁlling-in pixels

in the inpainting domain. As discussed in (Fedorov

et al., 2015), the tensors are sensitive to blur, tending

to larger neighbourhoods in blurry regions. To com-

pensate for this, we allow the parameter r (in equa-

tion 8) to vary during the correspondence map estima-

tion. That is, while T

ˆu

(ϕ(x)) is always computed with

the ﬁxed r, say r

(a given parameter of the method),

in the computation of T

(x) we consider a few val-

ues of r smaller than r

(around 5) and select the one

giving the smallest patch distance D

between p

(x)

and p

ˆu

(ϕ(x)). Let us note, that to be able to compare

patches, computed with different values of r, we scale

the normalized circles to circles of radius one.

5 EXPERIMENTAL RESULTS

In this section we present results obtained by the pro-

posed method. For all the experiments in this section,

we compare our results with the ones obtained by the

multiscale NL-Means method (Wexler et al., 2007;

Kawai et al., 2009) which we ﬁnd to be a representa-

tive exemplar-based image inpainting method operat-

ing with only translations of patches. Whenever pos-

sible, we also compare against the method of (Mans-

ﬁeld et al., 2011) with a single scale and considering

rotations, and the method of (Huang et al., 2014). In

both cases we use the authors’ implementations.

As a sanity check we ﬁrst test the proposed

method on a synthetic example, displayed in Figure 4.

We take a textured image and create an afﬁnely trans-

formed version of it. We select a part of the trans-

formed image as the inpainting domain. Instead of

using the rest of the transformed image to copy in-

formation from, we make the original (not trans-

formed) image to be the source. Let us remark that the

ground truth afﬁnity is not provided to the algorithm,

hence, we test the ability of the proposed method to

identify and copy afﬁnely transformed patches. We

do not show any results for (Mansﬁeld et al., 2011)

and (Huang et al., 2014) for this experiment, since the

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

Figure 4: First row: source image, target image with the inpainting domain shown in red, and close-ups around the inpainting

area of the NL-Means result and the result of our method. Second row: evolution of the inpainting domain over iterations of

our method (every third iteration).

Figure 5: First row: image with the inpainting domain shown in red. Second row: close-ups around the inpainting area of

the NL-Means result, the result of (Mansﬁeld et al., 2011) (considering rotations), the result of (Huang et al., 2014), and the

result of our method. Third row: evolution of the inpainting domain over iterations of our method (every third iteration).

available implementations do not support the use of a

separate image as a source.

A more realistic case would be associated with a

more general transformation. Since for planar objects

a projective transformation can be locally approxi-

mated by an afﬁnity, in the second example (shown

in Figure 5) we test the robustness of our method

in the reconstruction of an image distorted by per-

spective. As usual in inpainting applications, in this

experiment we use the known part of the image as

source. We compare our method with the NL-Means

method, that works only with translations, and addi-

tionally with the method of (Mansﬁeld et al., 2011)

in the mode when the rotations are also considered,

and the method of (Huang et al., 2014). Note that the

latter method successfully determines a single plane

in the image and, as expected, achieves a good recon-

struction.

Afﬁne Invariant Self-similarity for Exemplar-based Inpainting

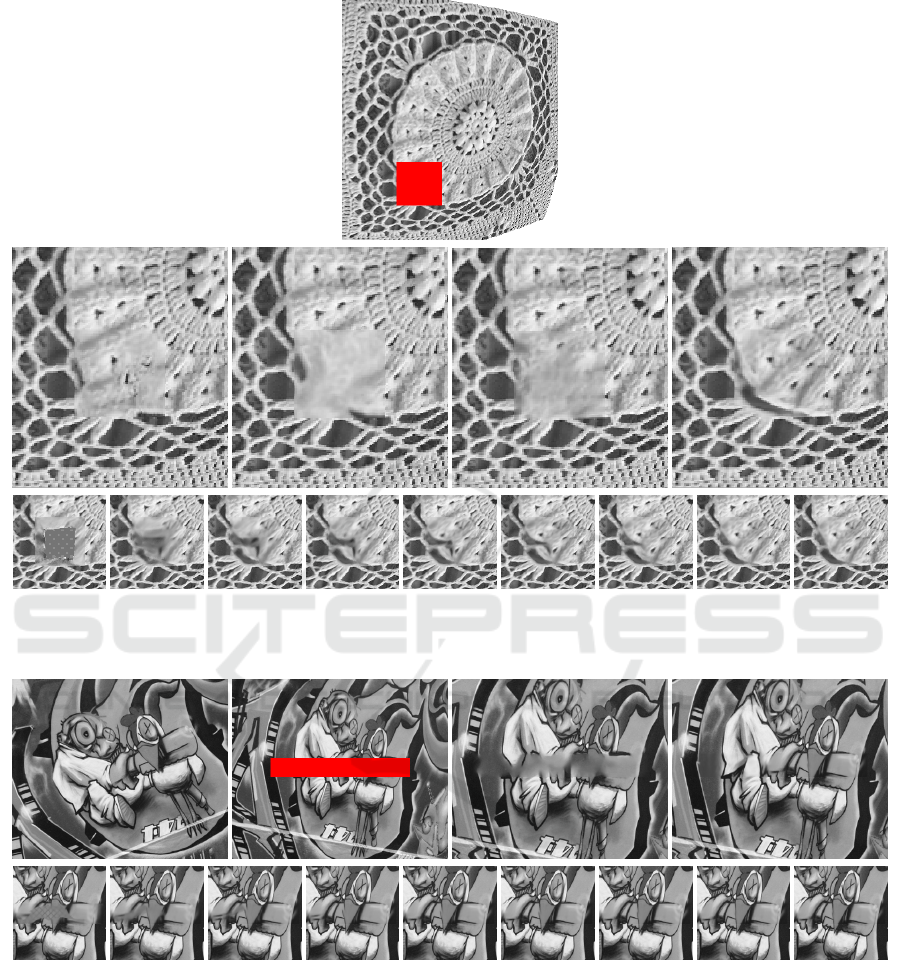
Figure 6: First row: image with the inpainting domain shown in red. Second row: close-ups around the inpainting area of

the NL-Means result, the result of (Mansﬁeld et al., 2011) (considering rotations), the result of (Huang et al., 2014), and the

result of our method. Third row: evolution of the inpainting domain over iterations of our method (every third iteration).

Figure 7: First row: source image, target image with the inpainting domain shown in red, and close-ups around the inpainting

area of the NL-Means result and the result of our method. Second row: evolution of the inpainting domain over iterations of

our method (every third iteration).

The third example (Figure 6) demonstrates the re-

construction of a texture with some lens distortion ap-

plied to it. The known part of the image is used as a

source and, like in all other experiments, just a ro-

tation of source patches is not sufﬁcient to obtain a

good result. As in the previous case, here we com-

pare our method with the NL-Means method (transla-

tions), the method of (Mansﬁeld et al., 2011) (transla-

tions and rotations), and the method of (Huang et al.,

2014) (projective transformation).

A ﬁnal experiment, which is also potentially in-

teresting for real applications, consists in inpainting

one view of a scene using information from another

view of the same scene. Figure 7 shows the results of

this experiment where we have applied the proposed

method to two views related by an unknown homog-

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

raphy. As before, we compare our result with the re-

sult of the NL-Means method.

Let us ﬁnally note that the method of (Mansﬁeld

et al., 2011) also supports rotations plus scalings.

However, we could not obtain meaningful results on

these examples for this mode. It seems that the addi-

tional variability added by the scalings makes it eas-

ier for the algorithm to be trapped in a bad local mini-

mum. For example, a constant region can be produced

by scaling a small uniform patch.

6 CONCLUSIONS

In this work we propose a new variational formula-

tion for exemplar-based inpainting that, for the ﬁrst

time, considers local full afﬁne transformations with

a tractable approximate optimization scheme. This is

possible thanks to the use of the afﬁne covariant ten-

sors and the associated afﬁne invariant metric, both

introduced in (Fedorov et al., 2015). These tensors

provide an efﬁcient way to determine a unique afﬁn-

ity putting in correspondence any pair of patches. If

the patches being compared are related by an afﬁnity,

then this afﬁnity is recovered.

The problem of exemplar-based inpainting is a

complex non-convex problem with many local min-

ima. As pointed out in (Cao et al., 2011), adding

transformations of patches makes it even more com-

plex. Intuitively, the added variability makes it harder

to distinguish “good” minima from other minima (a

single pixel can be scaled to match a constant patch).

We believe that the tensors are beneﬁcial in this re-

spect, because they constrain the number of ways in

which a source patch can be transformed to match a

target patch, thus eliminating some of the variability.

This also allows us to design faster and more accurate

minimization algorithms without the need to search

the parameter space of the transformation family.

The proposed method works at a single scale. To

better handle larger inpainting domains it would be

desirable to develop a multiscale scheme, as is cus-

tomary in the literature (Wexler et al., 2007; Kawai

et al., 2009; Arias et al., 2011). However, extend-

ing the multiscale approach to the problem of inpaint-

ing using afﬁnely transformed patches is not trivial,

since the ﬁltering with an isotropic Gaussian breaks

the afﬁne invariance. Adapting multiscale inpainting

approaches to this context is an interesting direction

for future research.

ACKNOWLEDGEMENTS

The ﬁrst, the second and the fourth authors acknowl-

edge partial support by MICINN project, reference

MTM2012-30772, and by GRC reference 2014 SGR

1301, Generalitat de Catalunya.

The second and third authors were partly founded

by the Centre National d’Etudes Spatiales (CNES,

MISS Project), BPIFrance and Rgion Ile de France, in

the framework of the FUI 18 Plein Phare project, the

European Research Council (advanced grant Twelve

Labours n246961), the Ofﬁce of Naval research

(ONR grant N00014-14-1-0023), and ANR-DGA

project ANR-12-ASTR-0035.

REFERENCES

Arias, P., Facciolo, G., Caselles, V., and Sapiro, G. (2011).

A variational framework for exemplar-based image in-

painting. International Journal of Computer Vision,

93:319–347.

Aujol, J.-F., Ladjal, S., and Masnou, S. (2010). Exemplar-

based inpainting from a variational point of view.

SIAM Journal on Mathematical Analysis, 42(3):1246–

1285.

Ballester, C., Bertalm

ıo, M., Caselles, V., Sapiro, G., and

Verdera, J. (2001). Filling-in by joint interpolation of

vector ﬁelds and gray levels. IEEE Transactions on

Image Processing, 10(8):1200–1211.

Ballester, C., Calderero, F., Caselles, V., and Facciolo, G.

(2014). Multiscale analysis of similarities between

images on riemannian manifolds. SIAM Journal Mul-

tiscale Modeling and Simulation, 12(2):616–649.

Ballester, C. and Gonzalez, M. (1998). Afﬁne invariant

texture segmentation and shape from texture by varia-

tional methods. Journal of Mathematical Imaging and

Vision, 9(2):141–171.

Barnes, C., Shechtman, E., Finkelstein, A., and Goldman,

D. B. (2009). PatchMatch: a randomized correspon-

dence algorithm for structural image editing. In ACM

SIGGRAPH 2009 Papers, pages 1–11. ACM.

Barnes, C., Shechtman, E., Goldman, D. B., and Finkel-

stein, A. (2010). The generalized PatchMatch cor-

respondence algorithm. In European Conference on

Computer Vision.

Bertalm

ıo, M., Sapiro, G., Caselles, V., and Ballester, C.

(2000). Image inpainting. In Proceedings of SIG-

GRAPH,, pages 417–424.

Buades, A., Coll, B., and Morel, J.-M. (2005). A non local

algorithm for image denoising. In Proceedings of the

IEEE Conference on CVPR, volume 2, pages 60–65.

Cao, F., Gousseau, Y., Masnou, S., and Prez, P. (2011). Ge-

ometrically guided exemplar-based inpainting. SIAM

Journal on Imaging Sciences, 4(4):1143–1179.

Chan, T. and Shen, J. H. (2001a). Mathematical models

for local nontexture inpaintings. SIAM J. App. Math.,

62(3):1019–43.

Afﬁne Invariant Self-similarity for Exemplar-based Inpainting

Chan, T. and Shen, J. H. (2001b). Nontexture inpainting by

curvature-driven diffusions. Journal of Visual Com-

munication and Image Representation, 12(4):436–

449.

Criminisi, A., P

erez, P., and Toyama, K. (2004). Region ﬁll-

ing and object removal by exemplar-based inpainting.

IEEE Trans. on IP, 13(9):1200–1212.

Demanet, L., Song, B., and Chan, T. (2003). Image in-

painting by correspondence maps: a deterministic ap-

proach. Applied and Computational Mathematics,

1100:217–50.

Drori, I., Cohen-Or, D., and Yeshurun, H. (2003).

Fragment-based image completion. In ACM SIG-

GRAPH 2003 Papers, volume 22, pages 303–12.

Efros, A. A. and Leung, T. K. (1999). Texture synthesis by

non-parametric sampling. In Proceedings of the IEEE

ICCV, pages 1033–38.

Fedorov, V., Arias, P., Sadek, R., Facciolo, G., and

Ballester, C. (2015). Linear multiscale analysis of

similarities between images on riemannian manifolds:

Practical formula and afﬁne covariant metrics. SIAM

Journal on Imaging Sciences, 8(3):2021–2069.

Foi, A. and Boracchi, G. (2012). Foveated self-similarity

in nonlocal image ﬁltering. Human Vision and Elec-

tronic Imaging XVII, 8291(1):829110.

Garding, J. and Lindeberg, T. (1994). Direct estimation of

local surface shape in a ﬁxating binocular vision sys-

tem. In Eklundh, Lecture Notes in Computer Science,

pages 365–376.

Gilboa, G. and Osher, S. J. (2008). Nonlocal operators with

applications to image processing. Multiscale Model-

ing and Simulation, 7(3):1005–1028.

arding, J. (1992). Shape from texture for smooth curved

surfaces in perspective projection. Journal of Mathe-

matical Imaging and Vision, 2(4):327–350.

arding, J. and Lindeberg, T. (1996). Direct computation

of shape cues using scale-adapted spatial derivative

operators. International Journal of Computer Vision,

17(2):163–191.

Hays, J. and Efros, A. (2007). Scene completion using mil-

lions of photographs. In SIGGRAPH, New York, NY,

USA. ACM.

Huang, J.-. B., Kopf, J., Ahuja, N., and Kang, S. B. (2013).

Transformation guided image completion. In Inter-

national Conference on Computational Photography,

pages 1–9.

Huang, J. B., Kang, S. B., Ahuja, N., and Kopf, J. (2014).

Image completion using planar structure guidance.

ACM Transactions on Graphics (Proceedings of SIG-

GRAPH 2014), 33(4):129:1–129:10.

Kawai, N., Sato, T., and Yokoya, N. (2009). Image inpaint-

ing considering brightness change and spatial locality

of textures and its evaluation. In Advances in Image

and Video Technology, pages 271–282.

Lowe, D. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60(2):91–110.

Mansﬁeld, A., Prasad, M., Rother, C., Sharp, T., Kohli, P.,

and van Gool, L. (2011). Transforming image comple-

tion. In Proceedings of BMVC, pages 121.1–121.11.

Masnou, S. (2002). Disocclusion: a variational approach

using level lines. IEEE Transactions on Image Pro-

cessing, 11(2):68–76.

Masnou, S. and Morel, J.-M. (1998). Level lines based dis-

occlusion. In Proceedings of IEEE ICIP, volume 3,

pages 259–263.

Matas, J., Chum, O., Urban, M., and Pajdla, T. (2004).

Robust wide-baseline stereo from maximally stable

extremal regions. Image and Vision Computing,

22(10):761–767.

Mikolajczyk, K. and Schmid, C. (2004). Scale & afﬁne in-

variant interest point detectors. International Journal

of Computer Vision, 60(1):63–86.

Pavi

c, D., Schonefeld, V., and Kobbelt, L. (2006). Inter-

active image completion with perspective correction.

The Visual Computer, 22(9-11):671–681.

Peyr

e, G. (2009). Manifold models for signals and im-

ages. Computer Vision and Image Understanding,

113(2):249–260.

Pizarro, L., Mr

azek, P., Didas, S., Grewenig, S., and Weick-

ert, J. (2010). Generalised nonlocal image smoothing.

International Journal of Computer Vision, 90:62–87.

Wang, Z. (2008). Image afﬁne inpainting. In Image Analy-

sis and Recognition, volume 5112 of Lecture Notes in

Computer Science, pages 1061–1070.

Wexler, Y., Shechtman, E., and Irani, M. (2007). Space-time

completion of video. IEEE Transactions on PAMI,

29(3):463–476.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications