
Recognizing Human Actions based on Extreme Learning Machines
Gr
´
egoire Lefebvre and Julien Cumin
Orange Labs, R&D, Meylan, France
Keywords:
Human Action Recognition, Extreme Learning Machines.
Abstract:
In this paper, we tackle the challenge of action recognition by building robust models from Extreme Learn-
ing Machines (ELM). Applying this approach from reduced preprocessed feature vectors on the Microsoft
Research Cambridge-12 (MSRC-12) Kinect gesture dataset outperforms the state-of-the-art results with an
average correct classification rate of 0.953 over 20 runs, when splitting in two equal subsets for training and
testing the 6, 244 action instances. This ELM based proposal using a multi-quadric radial basis activation
function is compared to other classical classification strategies such as Support Vector Machines (SVM) and
Multi-Layer Perceptron (MLP) and advancements are also presented in terms of execution times.
1 INTRODUCTION
Human activity recognition is one of the main chal-
lenging topics in computer vision research. Its im-
portance may be explained by many successes for in-
stance in video games, video surveillance, sport anal-
ysis, back and neck pain control, sign language un-
derstanding, human-robot interaction, etc. Various
types of activities indeed appear in everyday life, such
as gestures, actions, human-object interactions, social
interactions and group activities.
Nevertheless, some issues still exist in human ac-
tion recognition automation: the first ones are in-
herent to user gesture productions, the other ones
come from data acquisitions. The classical recogni-
tion methods are often biased by numerous factors:
dynamical variations (dynamic and phlegmatic users),
temporal variations (slow and fast users), physical
variations (device weight, user morphology, left or
right-handed users, contextual environment, parallel
user activities, etc.), paradigm variations (mono ver-
sus multi users, open or closed world paradigm, etc.),
and cultural interpretation variations (i.e. one ges-
ture may have different meanings regarding several
cultures). Other difficulties impacting the data ac-
quisition system are the presence of occlusions, non-
rigid motions, view-point changes, background inter-
ferences, etc.
Therefore, a human action recognition system is
designed to deal with these issues. The early meth-
ods propose pose estimators as action features and
build appearance models based on shape (Blank et al.,
2005) or motion (Efros et al., 2003) information.
Then, in order to avoid segmentation and object track-
ing issues, local features and bag-of-features repre-
sentations strategies are proposed. This offers com-
pact action descriptors to be classified as dense tra-
jectories (Wang et al., 2011a) or sparse motion vec-
tors (Kantorov and Laptev, 2014). In contrast, other
studiesdeal with mid-level representations (Jain et al.,
2013) and temporal models (Amer et al., 2013). On
one side, the main objectives are to group point tra-
jectories into tentative action parts by similarity in
motion and appearance and then learn discriminative
models with latent assignment of action parts. This
allows in particular to localize discriminative action
parts. On the other side, temporal models describe
actions as a sparse sequence of spatio-temporally lo-
calized frames. This approach models longer events
by temporal logical composition of simple actions.
On action data, preprocessing steps such as spatio-
temporal segmentation and description are time con-
suming. Likewise, parameterizing and training a ded-
icated classifier can be very challenging. That is why,
in this paper, we propose an action classification sys-
tem based on Extreme Learning Machines (Huang
et al., 2004) in order to operate fast and robust recog-
nitions on action data with compact feature vectors.
This paper is organized as follows. Section 2
presents related works on action recognition. In Sec-
tion 3, we explain in details Extreme Learning Ma-
chines (ELM). Then, Section 4 describes our results
with a comparison to classical approaches. Finally,
our conclusions and perspectives are drawn.
478
Lefebvre, G. and Cumin, J.
Recognizing Human Actions based on Extreme Learning Machines.
DOI: 10.5220/0005675004780483
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 478-483
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
2 RELATIVE STUDIES
Designing an automatic action recognition system
based on video analysis is already challenging, but
when users want an interactive system based on nat-
ural human interactions, the challenge is even higher.
Indeed, when designing an iterative action recogni-
tion system, the two main priorities are reducing la-
tency when users are interacting with it and maxi-
mizing the action recognition scores in order to of-
fer better user experiences. These two properties are
influenced by the action feature vector dataset to be
modeled in a robustness and speed classifier.
In (Ellis et al., 2013), the two aspects are taken
into account with a latency-aware learning formu-
lation in order to train a logistic regression model
(LRM). The contribution is to distinguish canoni-
cal poses from body motions to reduce ambiguity
for action recognition. Their experimental results
on the Microsoft Research Cambridge-12 (MSRC-12)
Kinect gesture dataset (Fothergill et al., 2012) show
improvements (i.e. an average correct classification
rate of 0.912 for a 4-cross validation) in opposition to
a bags of visual words and a conditional random field
strategy. The trade-off between latency and accuracy
is then guided by a Frame Based Descriptor (FBD) of
size 2276. The information support from the 3D body
joint motions appears then to be crucial.
Likewise, in (Hussein et al., 2013), the construc-
tion of discriminative descriptors from 3D skeleton
data is obtained in order to optimize the recognition
system. Encoding the correlation between joint tra-
jectories during space and time, they propose a Tem-
poral Hierarchy of Covariance Descriptor (THCD).
This descriptor has a fixed size of 7320 and the final
classification is operated by a linear SVM classifier.
On the MSRC-12 dataset, the experiments give an av-
erage correct classification rate of 0.917 for a 20-cross
validation when splitting 50% of the dataset for train-
ing and testing steps.
A more recent study by (Vemulapalli et al., 2014)
also uses a SVM classifier to build an action recog-
nition system. Consequently, it is again the choice
of the feature descriptors which influences the global
recognition accuracy. The authors propose to model
the geometric relationships between 3D body parts.
Human actions are then modeled as curves in this
Lie group based on 3D rigid body motions which are
members of the Special Euclidean Group SE(3). The
feature vector is then of size 2280 and the correct clas-
sification rate are very challenging with 0.9088 on the
Florence3D-Action dataset (Seidenari et al., 2013).
In this paper, we propose a more reduced feature
vector of size 1200 and a fast ELM classification.
3 EXTREME LEARNING
MACHINES
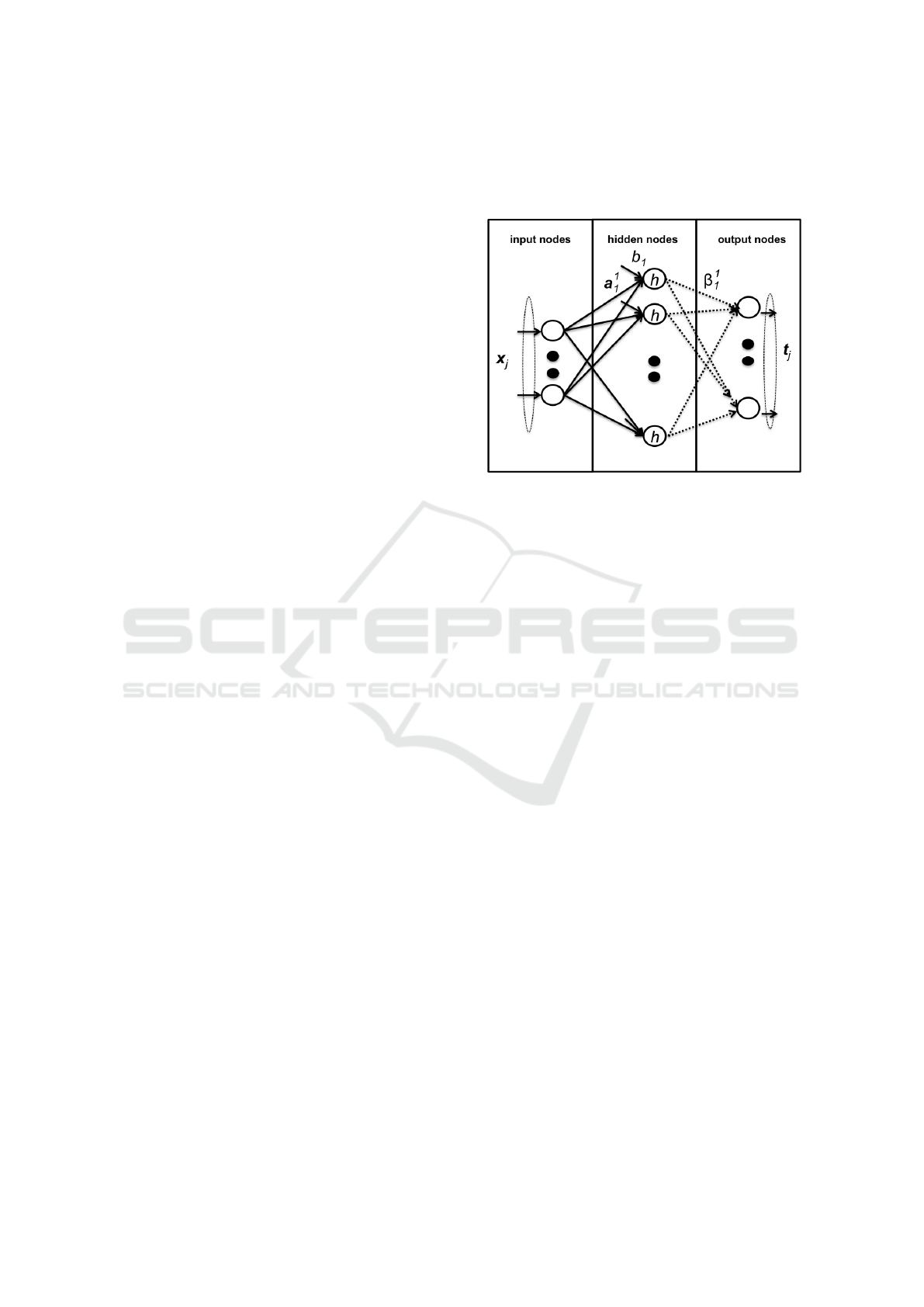
Figure 1: Single feed-forward network.
Deep learning methods are nowadays widely used in
machine learning. With recent successes on visual
object recognition (Farabet et al., 2013) or speech
recognition (Graves et al., 2013) and iconic gesture
recognition (Lefebvre et al., 2015), deep architectures
using feed-forward neural networks (e.g. Convolu-
tional Neural Networks (Lecun et al., 1998)) or recur-
rent neural networks (e.g. Long Short Term Memory
(Hochreiter and Schmidhuber, 1997)) are limited to
some issues: a relatively slow training speed, over-
fitting problems and a relatively high number of pa-
rameters needed to be tuned.
Inspired by previous studies on Radial Basis Func-
tion (RBF) networks (see (Broomhead and Lowe,
1988; Chen et al., 1991)), Huang et al. present ELM
in (Huang et al., 2004) in order to deal with these is-
sues for classification and regression problems. An
ELM is a single layer feed-forward network (SLFN)
with only two parameters: the number of hidden
nodes and the choice of an activation function (see
Figure 1). In comparison to the traditional back-
propagation algorithm based on a gradient descent in
order to minimize the network error between the pro-
duced output and the desired target, the ELM method
initializes randomly the network weights and then
computes directly a Moore-Penrose pseudo-inverse
matrix to generate a unique solution. In various fields
(e.g. regression problems, medical diagnosis applica-
tion, diabetes protein sequence classification), ELM
shows some promising features such as generalization
ability, robustness, controllability and a fast learning
process (see (Huang et al., 2015)).
Numerous studies propose some extensions to ad-
dress some ELM issues, such as the network hid-
Recognizing Human Actions based on Extreme Learning Machines
479

Figure 2: Human action from MSRC-12 Kinect gesture dataset: Wind up the music.
den layer output matrix singularity. In (Wang et al.,
2011b), the Effective ELM (EELM) algorithm ex-
ploits the strictly dominant criterion for non-singular
matrices. In (Huang et al., 2012), an Optimization-
based regularized ELM (ORELM) enhances the gen-
eralization properties of ELM. Likewise, improve-
ments are published in (Iosifidis et al., 2014) in order
to exploit the training data dispersion with a Mini-
mum Variance ELM (MVELM).
Let’s introduce some notations. For N arbitrary
distinct samples (x
j
, t
j
), we note data samples by
x
j
= [x
1
j
, x
2
j
, ..., x
n
j
]
|
∈ R
n
and the relative targets by
t
j
= [t
1
j
, t
2
j
, ..., t
m
j
]
|
∈ R
m
. Let be a
i
= [a
1
i
, a
2
i
, ..., a
n
i
]
|
the weight vector connecting the i
th
hidden node and
the input nodes, and b
i
∈ R is the respective bias
of the i
th
hidden node. The weight vector connect-
ing the i
th
hidden node and the output nodes is β
i
=
[β
1
i
, β
2
i
, ..., β
m
i
]
|
and the activation function h is usu-
ally a Sigmoid or a Radial Basis Function. Conse-
quently, a SLFN with L hidden neurons is defined by:
∀ j ∈ {1, . . . , n}, t
j
=
L
∑
i=1
β
i
h(a
i
· x
j
+ b
i
) (1)
Equation 1 can be written with H ∈ R
N×L
the hid-
den layer output matrix of the network, B ∈ R
L×m
and
T ∈ R
N×m
, as defined by:
HB = T. (2)
Therefore, the SFLN learning process corre-
sponds now to find the Equation 2 least squares so-
lution. The solution is provided by:
ˆ
B = H
†
T. (3)
In Equation 3, H
†
represents Moore-Penrose gen-
eralized inverse of the hidden layer output matrix H.
As described in (Zhang et al., 2013), the optimal so-
lution
ˆ
B has the following features:
1. this algorithm can gain the minimal training error;
2. this algorithm can get the optimal generalization
capability of the minimum paradigm of the output
connection weights and network;
3.
ˆ
B is unique and can avoid local optimal solutions.
Consequently, the ELM learning speed is fast and
can reach the solution straightforward without facing
local minima or over-fitting issues. Recent studies
(Minhas et al., 2010; Iosifidis et al., 2014) proposed
ELM for Human Action Recognition based on bags of
visual words. Here, we build our system on specific
feature vectors using directly four joint trajectories,
described hereafter.
4 EXPERIMENTS
4.1 Protocols
Our experiments are based on the Microsoft Research
Cambridge-12 (MSRC-12) Kinect gesture dataset
(see for details (Fothergill et al., 2012) and an action
sample in Figure 2). This dataset is composed of 594
sequences of human actions from 30 people perform-
ing 12 gestures. The gesture set is composed of 6
iconic gestures: crouch and hide (duck), shoot with a
pistol, throw an object, change weapon, kick to attack,
put on night vision goggles and 6 metaphoric gestures:
start the music (lift outstretched arms), navigate to
next menu (push right), wind up the music, take a bow,
protest the music, lay down the song tempo (beat both
arms). In total, 6, 244 gesture instances are stored us-
ing 20 body joint positions captured at 30Hz. Each
body joint is 3-dimensional.
In this study, we evaluate the effectiveness of our
approach with a reduced training set using 50% of
the MSRC-12 dataset (i.e. 3, 122 training instances
and 3, 122 test instances). This configuration ap-
pears to be the less advantageous and the more chal-
lenging one according to (Hussein et al., 2013). In
order to compare our results with two state-of-the-
art methods: Frame-Based Descriptors and Logistic
Regression Models (Ellis et al., 2013) (FBD+LRM)
and Temporal Hierarchy of Covariance Descriptors
and Support Vector Machines (Hussein et al., 2013)
(THCD+SVM), we perform a 20-cross validation as
in (Hussein et al., 2013) and the comparison is then
based on the average correct classification and the as-
sociated standard deviation. We evaluate as well two
other classical classifiers (i.e. SVM and MLP) with
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
480
the Weka data mining software (Hall et al., 2009) on
our feature vectors (FV) to prove the relevance of our
(FV+ELM) approach.
Our feature vectors are obtained from the concate-
nation of the four 3D body joints corresponding to the
two hands and the two feet, for each time period. We
first filter the 12-D signal with a low-pass filter of pa-
rameter 0.7. Then a normalization is operated and an
interpolation is computed to get an equal duration of
3333 ms for all actions. The feature vector is finally
the concatenation of all values through time, giving
a dimension of 1200. This can be viewed as a prior
fusion process.
The choice of all parameters in the following
study is given by analyzing a preliminary study with
1200 training instances and 1200 validation instances
extracted from the original 3, 122 training instances.
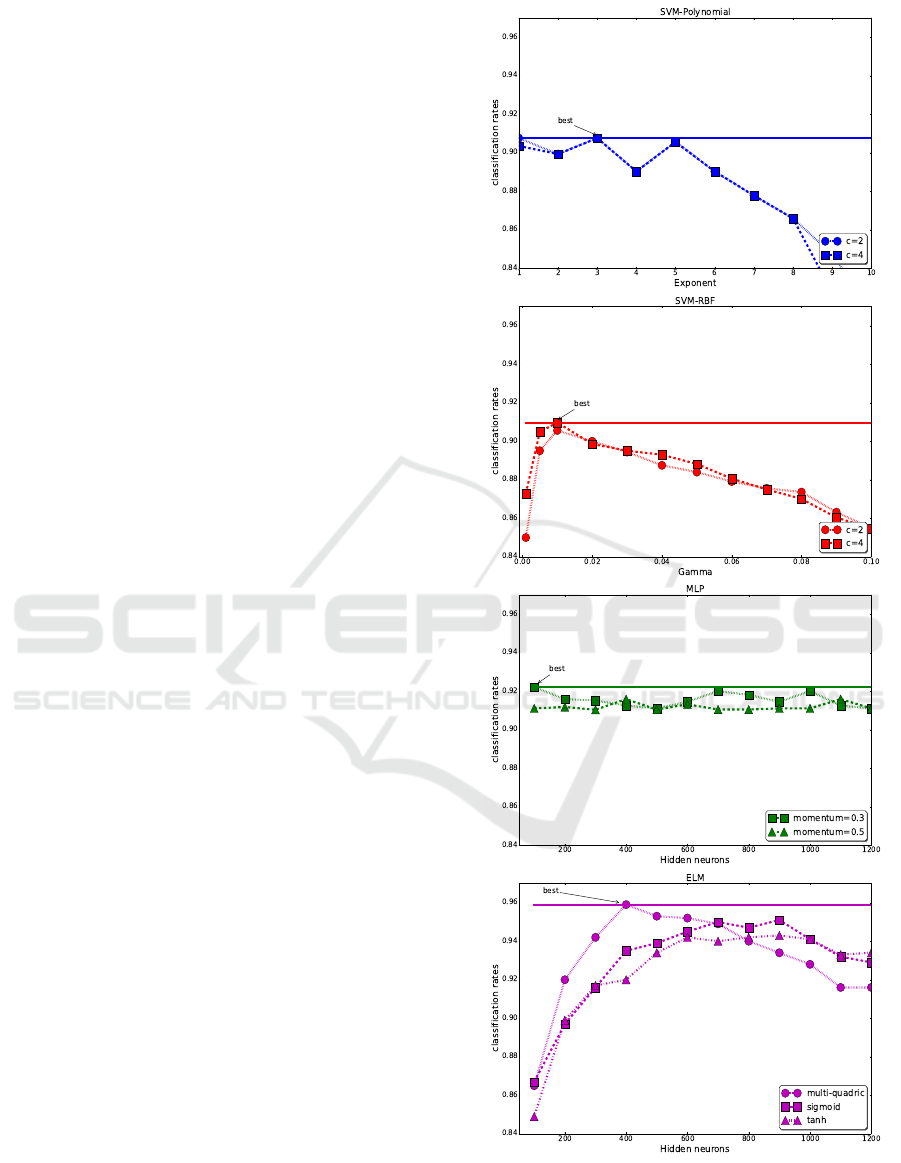
For instance, Figure 3 shows some tested con-
figurations for all classifiers. This figure gives the
best ELM performance with 400 hidden nodes and
a multi-quadric radial basis activation function as op-
posed to other ELM configurations with sigmoid and
hyperbolic tangent activation functions. Likewise, the
preliminary results on the good fit of our feature vec-
tors with a SVM classifier give better performances
with a RBF kernel with γ = 0.005 and c = 4, com-
pared to a polynomial kernel. Our evaluation on MLP
gives a best configuration with 100 hidden neurons,
600 learning epochs and a learning rate of 0.005 with
a hyperbolic tangent as an activation function.
Consequently, the final configurations of the clas-
sifiers reported in the next section are the following:
• SVM uses a RBF kernel with γ = 0.005 and c = 4;
• MLP uses one layer of 100 hidden neurons, 600
learning epochs and a learning rate of 0.005 with
a hyperbolic tangent as an activation function;
• ELM uses 400 hidden nodes and a multi-quadric
radial basis activation function.
4.2 Classification Results
Table 1 outlines the global performances of each hu-
man action recognition strategy. Our solution based
on our feature vectors FV and an ELM classifier gives
the best average correct classification rate of 0.953
with a reduced standard deviation of 0.003. The re-
sults previously published were respectively 0.912
for FBD+LRM (Ellis et al., 2013) (n.b. the authors
used only a 4 folds cross-validation) and 0.917 for
THCD+SVM (Hussein et al., 2013). Consequently,
these results show that feature vectors extracted only
from four joint data can be an adequate informa-
tion support for human action recognition. More-
Figure 3: Classification rate on an evaluation dataset (1200
training instances, 1200 evaluation instances).
Recognizing Human Actions based on Extreme Learning Machines
481
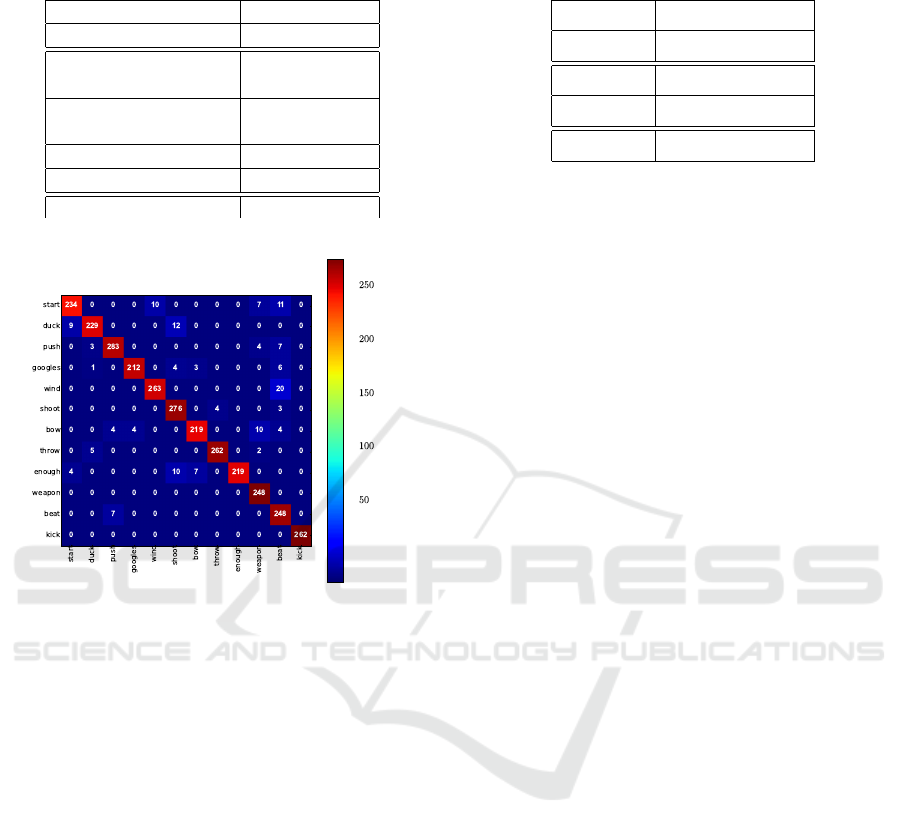
Table 1: Average correct Classification Rates (ACR) and
Standard Deviations (SD) on MSRC-12.
Database MSRC-12
Methods ACR & SD
FBD+LRM 0.912 ± -
(Ellis et al., 2013)
THCD+SVM 0.917 ± -
(Hussein et al., 2013)
FV+SVM 0.898 ± 0.002
FV+MLP 0.906 ± 0.008
FV+ELM 0.953 ± 0.003
Figure 4: One resulting confusion matrix on MSRC-12,
when applying our FV+ELM strategy.
over, we demonstrate on our protocol the effective-
ness of the ELM classifier as opposed to the SVM
and MLP classifiers (with respectively 0.898 ± 0.002
and 0.906 ± 0.008 of correct classification rate).
A main conclusion of an analysis of confusion ma-
trices (see Figure 4 showing one tested configuration)
is that our FV+ELM method presents 20 misclassi-
fication between wind up the music (wind) and lay
down the tempo (beat). In fact, these two actions
share common trajectories with respectively circular
movements with both arms, in front of the body, for
the first action, and hand beat movements in the air for
the second action. Likewise, we can observe some
confusions between duck and shoot, start and beat,
start and wind up, and enough and shoot.
4.3 Computing Times
In addition, we report the computing times for the 3
methods using the same feature vectors in order to
learn 3, 122 gestures and testing 3, 122 gestures of the
MSRC-12 database (c.f. Table 2). This experiment
was executed on an Intel Core i5 CPU clocked at 2.67
Table 2: Average Computing Times (ACT) and Standard
Deviation (SD) in seconds on MSRC-12.
Database MSRC-12
Methods ACT & SD
FV+SVM 8.875 ± 0.182
FV+MLP 793.883 ± 0.194
FV+ELM 4.865 ± 0.102
GHz with 3.42 GB of RAM.
These experimental results show that the comput-
ing times for the ELM based solution is fast (i.e.
around 4.865 seconds in average). On the contrary,
the FV+SVM based solution requires more time to
learn and test the 6, 244 gestures (i.e. around 8.875
seconds in average). The FV+MLP based method
needs around 793.883 seconds in average but this is
mainly due to the learning process using 600 epochs
to build the best neural model in this case.
Consequently, our proposed FV+ELM system,
achieving the best result performances in a multi-user
configuration with a fast recognition computing time,
is a very challenging solution.
5 CONCLUSIONS AND
PERSPECTIVES
In this article, we presented a human action recogni-
tion system based on specific feature vectors FV and a
ELM classifier. Using the MSRC-12 dataset in order
to cover real world challenging cases, we showed that
the proposed approach proves to be superior to some
state-of-the-art methods. It also outmatches its neural
counterpart MLP, both in classification and process-
ing time on our experiments.
Some perspectives would be to experiment Echo
State Networks (ESN (Tong et al., 2007)) with raw
temporal input data to preserve the temporal correla-
tion and detect gestural grammar inside each human
action.
REFERENCES
Amer, M., Todorovic, S., Fern, A., and Zhu, S.-C. (2013).
Monte carlo tree search for scheduling activity recog-
nition. In Computer Vision (ICCV), 2013 IEEE Inter-
national Conference on, pages 1353–1360.
Blank, M., Gorelick, L., Shechtman, E., Irani, M., and
Basri, R. (2005). Actions as space-time shapes. In
Computer Vision, 2005. ICCV 2005. Tenth IEEE Inter-
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
482

national Conference on, volume 2, pages 1395–1402
Vol. 2.
Broomhead, D. S. and Lowe, D. (1988). Multivari-
able Functional Interpolation and Adaptive Networks.
Complex Systems 2, pages 321–355.
Chen, S., Cowan, C., and Grant, P. (1991). Orthogonal
least squares learning algorithm for radial basis func-
tion networks. Neural Networks, IEEE Transactions
on, 2(2):302–309.
Efros, A., Berg, A., Mori, G., and Malik, J. (2003). Rec-
ognizing action at a distance. In Computer Vision,
2003. Proceedings. Ninth IEEE International Confer-
ence on, pages 726–733 vol.2.
Ellis, C., Masood, S. Z., Tappen, M. F., Laviola, Jr., J. J.,
and Sukthankar, R. (2013). Exploring the trade-off
between accuracy and observational latency in action
recognition. Int. J. Comput. Vision, 101(3):420–436.
Farabet, C., Couprie, C., Najman, L., and LeCun, Y. (2013).
Learning hierarchical features for scene labeling. Pat-
tern Analysis and Machine Intelligence, IEEE Trans-
actions on, 35(8):1915–1929.
Fothergill, S., Mentis, H. M., Kohli, P., and Nowozin, S.
(2012). Instructing people for training gestural inter-
active systems. In Konstan, J. A., Chi, E. H., and
H
¨
o
¨
ok, K., editors, CHI, pages 1737–1746. ACM.
Graves, A., Mohamed, A., and Hinton, G. E. (2013).
Speech recognition with deep recurrent neural net-
works. In IEEE International Conference on Acous-
tics, Speech and Signal Processing, ICASSP 2013,
Vancouver, BC, Canada, May 26-31, 2013, pages
6645–6649.
Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,
P., and Witten, I. H. (2009). The weka data mining
software: An update. In SIGKDD Explorations, vol-
ume 11.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural Comput., 9(8):1735–1780.
Huang, G., Huang, G.-B., Song, S., and You, K. (2015).
Trends in extreme learning machines: A review. Neu-
ral Networks, 61(0):32 – 48.
Huang, G.-B., Zhou, H., Ding, X., and Zhang, R. (2012).
Extreme learning machine for regression and mul-
ticlass classification. Systems, Man, and Cyber-
netics, Part B: Cybernetics, IEEE Transactions on,
42(2):513–529.
Huang, G.-B., Zhu, Q.-Y., and Siew, C.-K. (2004). Extreme
learning machine: a new learning scheme of feedfor-
ward neural networks. In Neural Networks, 2004. Pro-
ceedings. 2004 IEEE International Joint Conference
on, volume 2, pages 985–990 vol.2.
Hussein, M. E., Torki, M., Gowayyed, M. A., and El-Saban,
M. (2013). Human action recognition using a tempo-
ral hierarchy of covariance descriptors on 3d joint lo-
cations. In Proceedings of the Twenty-Third Interna-
tional Joint Conference on Artificial Intelligence, IJ-
CAI ’13, pages 2466–2472. AAAI Press.
Iosifidis, A., Tefas, A., and Pitas, I. (2014). Minimum
variance extreme learning machine for human action
recognition. In Acoustics, Speech and Signal Process-
ing (ICASSP), 2014 IEEE International Conference
on, pages 5427–5431.
Jain, A., Gupta, A., Rodriguez, M., and Davis, L. (2013).
Representing videos using mid-level discriminative
patches. In Computer Vision and Pattern Recogni-
tion (CVPR), 2013 IEEE Conference on, pages 2571–
2578.
Kantorov, V. and Laptev, I. (2014). Efficient feature ex-
traction, encoding, and classification for action recog-
nition. In Computer Vision and Pattern Recogni-
tion (CVPR), 2014 IEEE Conference on, pages 2593–
2600.
Lecun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).
Gradient-based learning applied to document recogni-
tion. Proceedings of the IEEE, 86(11):2278–2324.
Lefebvre, G., Berlemont, S., Mamalet, F., and Garcia, C.
(2015). Inertial gesture recognition with BLSTM-
RNN. In Koprinkova-Hristova, P., Mladenov, V.,
and Kasabov, N. K., editors, Artificial Neural Net-
works, volume 4 of Springer Series in Bio-/Neuro-
informatics, pages 393–410. Springer International
Publishing.
Minhas, R., Baradarani, A., Seifzadeh, S., and
Jonathan Wu, Q. M. (2010). Human action recogni-
tion using extreme learning machine based on visual
vocabularies. Neurocomput., 73(10-12):1906–1917.
Seidenari, L., Varano, V., Berretti, S., Del Bimbo, A., and
Pala, P. (2013). Recognizing actions from depth cam-
eras as weakly aligned multi-part bag-of-poses. In
Computer Vision and Pattern Recognition Workshops
(CVPRW), 2013 IEEE Conference on, pages 479–485.
Tong, M. H., Bickett, A. D., Christiansen, E. M., and Cot-
trell, G. W. (2007). Learning grammatical structure
with echo state networks. Neural Networks, 20(3):424
– 432. Echo State Networks and Liquid State Ma-
chines.
Vemulapalli, R., Arrate, F., and Chellappa, R. (2014). Hu-
man action recognition by representing 3d skeletons
as points in a lie group. In Computer Vision and Pat-
tern Recognition (CVPR), 2014 IEEE Conference on,
pages 588–595.
Wang, H., Klaser, A., Schmid, C., and Liu, C.-L. (2011a).
Action recognition by dense trajectories. In Computer
Vision and Pattern Recognition (CVPR), 2011 IEEE
Conference on, pages 3169–3176.
Wang, Y., Cao, F., and Yuan, Y. (2011b). A study on effec-
tiveness of extreme learning machine. Neurocomput-
ing, 74(16):2483–2490.
Zhang, Y., Ding, S., Xu, X., Zhao, H., and Xing, W. (2013).
An algorithm research for prediction of extreme learn-
ing machines based on rough sets. Journal of Comput-
ers, 8(5).
Recognizing Human Actions based on Extreme Learning Machines
483
