Multiobjective Bacterial Foraging Optimization using Archive Strategy

Cuicui Yang and Junzhong Ji

College of Computer, Beijing University of Technology, Beijing Municipal Key Laboratory of Multimedia and

Intelligent Software, Pingleyuan 100, Chaoyang District, Beijing, China

Keywords:

Bacterial Foraging Optimization, Archive Strategy, Conjugation, Multiobjective Optimization.

Abstract:

Multiobjective optimization problems widely exist in engineering application and science research. This paper

presents an archive bacterial foraging optimizer to deal with multiobjective optimization problems. Under

the concept of Pareto dominance, the proposed algorithm uses chemotaxis, conjugation, reproduction and

elimination-and-dispersal mechanisms to approximate to the true Pareto fronts in multiobjective optimization

problems. In the optimization process, the proposed algorithm incorporates an external archive to save the

nondominated solutions previously found and utilizes the crowding distance to maintain the diversity of the

obtained nondominated solutions. The proposed algorithm is compared with two state-of-the-art algorithms

on four standard test problems. The experimental results indicate that our approach is a promising algorithm

to deal with multiobjective optimization problems.

1 INTRODUCTION

The multiobjective optimization problem (MOP) usu-

ally involves more than one conﬂicting objectives that

need to be optimized simultaneously and is an im-

portant class of scientiﬁc and engineering problems

in real-world (Deb, 2001). The solution to a MOP

is a set of trade-off solutions known as Pareto opti-

mal solutions or non-dominated solutions which can-

not improve all the objectives simultaneously. Evolu-

tionary computation methods based on Darwin’s bi-

ological evolution theory deal with a group of candi-

date solutions, which makes that they are natural to

be used to handle multiobjective optimization prob-

lems (MOPs). In the past two decades, researchers

have proposed a variety of evolutionary computation-

based approaches for solving MOPs (Deb, 2001;

Coello Coello CA, Van Veldhuizen DA, Lamont GB,

2007), such as the well-known algorithms PESA-

II (Corne D W, Jerram N R, Knowles J D, et al,

2001), NSGA-II (Deb K, Pratap A, Agarwal S, et

al, 2002) and SPEA2 (E Zitzler, M Laumanns, L

Thiele, 2002). Evolutionary multiobjective optimiza-

tion (EMO) that uses evolutionary computation meth-

ods to solve MOPs has become a relatively hot re-

search area.

In recent years, some new bio-inspired optimiza-

tion technologies have been successfully introduced

to deal with MOPs, where Particle swarm optimiza-

tion (PSO) is a prominent example. So far, there

have been a number of methods based on PSO for

solving MOPs (X Li, 2003; Coello C A C, Pulido

G T, Lechuga M S, 2004; Tripathi P K, Bandyopad-

hyay S, Pal S K, 2007). Bacterial foraging opti-

mization (BFO) is another popular bio-inspired op-

timization technology which simulates the foraging

behavior of E. coli bacteria (K.M. Passino, 2002).

BFO has been proved to be an efﬁcient optimiza-

tion method for single objective optimization prob-

lems (Agrawal V, Sharma H, Bansal J C, 2011), and

more recently researchers have also shown promising

results for MOPs (Panigrahi B K, Pandi V R, Das

S, et al, 2010; Guzm ´an M A, Delgado A, De Car-

valho J, 2010; Niu B, Wang H, Tan L, et al, 2012;

Niu B, Wang H, Wang J, et al, 2013). However, to

the best of our knowledge, none of these algorithms

incorporate an external archive to preserve the elitism

solutions, namely, there is no way to keep the non-

dominated solutions found previously in the optimiza-

tion process. Elitism-preservation is an importance

strategy in multiobjective search, which has been rec-

ognized and supported experimentally (Parks G T,

Miller I, 1998; Zitzler E, Deb K, Thiele L, 2000).

To further explore the potential of BFO algorithm in

ﬁnding Pareto optimal solutions for MOPs, this pa-

per presents an archive bacterial foraging optimizer

for multiobjective optimization, called as MABFO.

MABFO mainly includes four optimization mech-

anisms: chemotaxis, conjugation, reproduction and

elimination-and-dispersal. The implements of these

Yang, C. and Ji, J.

Multiobjective Bacterial Foraging Optimization using Archive Strategy.

DOI: 10.5220/0005668601850192

In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 185-192

ISBN: 978-989-758-173-1

185

mechanisms are different from other current meth-

ods based on BFO. More improtant, MABFO incor-

porates an external archive to save the nondominated

solutions previously found and uses the crowding dis-

tance to maintain the diversity of the nondominated

solutions. These strategies are conducive to produce

well-distributed and high-quality solutions.

MABFO is validated on four standard test prob-

lems and compared against two start-of-the-art EMO

approaches NSGA-II (Deb K, Pratap A, Agarwal S,

et al, 2002) and SPEA2 (E Zitzler, M Laumanns, L

Thiele, 2002). The experimental results indicate that

MABFO is a promising algorithm and can be consid-

ered an alternative to deal with MOPs.

The remainder of the paper is structured as fol-

lows. Section II brieﬂy introduces basic concepts in-

volving MOPs. Section III presents the details of the

MABFO algorithm. We then present experiments in

section IV, and ﬁnally, section V concludes the paper.

2 BASIC CONCEPTS

A MOP can be described as the problem of ﬁnding

a vector of decision variables that optimizes a vector

function and satisﬁes some restrictions. Without loss

of generality, a MOP is formulated as follows (Deb,

2001):











min y = F(x) = ( f

(x), f

(x),· ·· , f

(x))

s.t. g

(x) ≤ 0, i = 1, 2,·· · , p

(x) = 0, j = 1,2, ··· , q

≤ x

, (1)

where x = (x

,··· ,x

) ∈ X ⊂ R

is a n-dimensional

decision vector, X represents a n-dimensional deci-

sion space, x

and x

are the upper and lower bound-

ary values of x

, respectively. y = (y

,··· ,x

) ∈

Y ⊂ R

is a m-dimensional objective vector, Y rep-

resents a m-dimensional objective space. F(x) is a

mapping function from n-dimensional decision space

to m-dimensional objective space. g

(x) ≤ 0 (i =

1,2,· ·· , p) and h

(x) = 0 ( j = 1, 2,··· , q) deﬁnes p

inequalities and q equalities, respectively.

In the following, we will list four deﬁnitions in-

volving MOPs.

Pareto Dominant: x

, x

are two feasible solu-

tions for problem (1), x

is Pareto dominant compared

with x

if and only if:

∀i = 1, 2,··· , m, f

) ≤ f

) ∧

∃ j = 1,2,··· ,m, f

) < f

)

. (2)

We call this relationship x

≻ x

, x

dominate x

, or

is dominated by x

Pareto Optimal Solution: Ω is the feasible solu-

tion set of problem (1), x

∗

∈ Ω, x

∗

is a Pareto optimal

solution if and only if:

¬∃x ∈ Ω : x ≻ x

∗

. (3)

Pareto Optimal Set: The Pareto optimal set of

problem (1) includes all the Pareto optimal solutions

and is given as follows:

∗

= {x

∗

|¬∃x ∈ Ω : x ≻ x

∗

}. (4)

Pareto Front: The Pareto front of problem (1)

includes all the objective vectors corresponding to X

∗

and is given as follows:

PF = { F(x

∗

) = ( f

∗

), f

∗

),· ·· , f

∗

))

∗

∈ X

∗

(5)

3 THE MABFO ALGORITHM

In this section, we will introduce MABFO algorithm.

Algorithm 1 is the framework of MABFO. In the fol-

lowing, we will describe its ﬁve important operators

chemotaxis, archive updating, conjugation, reproduc-

tion and elimination-and-dispersal as Algorithm 1

shown.

Algorithm 1: MABFO algorithm (main loop).

Input: Different parameters:

: maximum number of chemotaxis,

: maximum number of reproduction,

: maximum number of elimination-and-dispersal,

N1: the size of population P,

N2: the maximum size of external archive A.

Output: A (Pareto optimal set)

1: Initialization: Generate an initial population P and an

empty archive A.

2: for l = 1 to N

3: for k = 1 to N

4: for j = 1 to N

a). Each bacterium in P takes a chemotaxis

process.

b). Archive updating: copy all nondominated

individuals in joint population of A and P to A.

If the size of A exceeds N2, then reduce it

based on the crowding distance.

c). Each bacterium takes a conjugation process.

5: end for

6: The population P perform a reproduction process

which selects N1 superior individuals in the joint

population P and A and then copy them to P.

7: end for

8: The population P perform an elimination-and-

dispersal process and update the archive A as step

4 b).

9: end for

10: Return A.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

186

3.1 Chemotaxis

Chemotaxis simulates the foraging movement of

E.coli bacteria through tumbling and swimming. To

absorb more nutrients, each bacterium tries to ﬁnd

food in two ways: tumbling and swimming. A bac-

terium tumbles in a random direction to exploratively

search for food. If the food is rich in the selected di-

rection, the bacterium will swim along this direction,

till the food gets bad or the bacterium has swum the

ﬁxed steps.

A random direction is a random unit vector in n-

dimensional space. In the original BFO algorithm, it

is very cumbersome to calculate a random unit vector

for each bacterium in every chemotaxis. In the pro-

posed MABFO algorithm, we use a simple unit vec-

tor e

with n dimensions as the chemotaxis direction,

in which only one component randomly selected (i.e.

the mth component) is either -1 or 1 and all the others

are 0. The method of updating a solution is given as

follows:

( j + 1, k, l) = x

( j,k,l) + c(i) e

, (6)

where x

( j,k,l) represents the ith bacterium at jth

chemotaxis, kth reproduction, lth elimination-and-

dispersal step. c(i) is the step size along the direc-

tion e

. The original BFO algorithm uses a ﬁxed

step size which would lead to bad convergence per-

formances (S Dasgipta, S Das, A Abraham and A

Biswas, 2009). In the proposed MABFO algorithm, a

dynamic step size is adopted and is given as follows:

c(i) = r (x

′

( j,k,l) − x

( j,k,l)), (7)

where r is a random number uniformly distributed

between −1 and 1, x

′

( j,k,l) denotes the mth com-

ponent of another different bacterium i

′

which is se-

lected randomly in P.

When bacterium i carries out a chemotaxis oper-

ator, it ﬁrst generates a direction e

and a step size

c(i) as described above, and then swims a step along

the direction e

according to Eq.(6). If the new solu-

tion x

( j+1,k,l) dominates the old solution x

( j,k,l),

bacterium i will swim another step in the direction e

according to Eq.(6). This process is continued until

bacterium i has swum the maximum steps N

or the

obtained new solution x

( j + 1,k,l) is dominated by

the old solution x

( j,k,l). Such chemotaxis mecha-

nism is an important driving force for locally opti-

mizing each candidate solution, where each bacterium

ties its best to search for non-dominated solutions.

3.2 Archive Updating

The main goal of the external archive is to keep a his-

torical record of the nondominated solutions obtained

in the search process. In MABFO, we use an exter-

nal archive A with a ﬁxed number N2. Whenever the

populationP carries out a chemotaxis process, we will

reselect all the nondominated solutions from the joint

population of P and A, and then update archive A by

copying them to A. If the size of A exceeds N2, an

archive truncation procedure is invoked, which itera-

tively remove individuals from A based on the crowd-

ing distance until the size of A is N2. At each itera-

tion, the individual which has the minimum distance

to another individual is removed according to the for-

mula:

dis(x

) < dis(x

) ⇔

∀ 0 < k < |Q| : σ

= σ

∨

∃ 0 < k < |Q| : [(∀0 < l < k : σ

= σ

) ∧ σ

< σ

]

(8)

where Q is a group of individuals, |Q| denotes the size

of Q and here Q = A. σ

is the distance of ith solution

to its kth nearest neighbor in Q.

The external archive A promises not to miss the

nondominated solutions found in the search process.

The crowding distance eliminates the individuals in

dense area, which can ensure the obtained solutions

distributed evenly. The using of external archive

and crowding distance is beneﬁcial to ﬁnd well-

distributed Pareto solutions.

3.3 Conjugation

Conjugation, as well as chemotaxis, is an important

biological behavior of bacteria. Bacterial conjugation

is the transfer of part of plasmid (genetic material)

from donor bacteria to recipient bacteria by directly

physical contact and is often regarded as the sex-

ual reproduction or mating between bacteria. Some

researchers have taken the bacterial conjugation as

a message passaging mechanism in their work (C

Perales-Grav´an, R Lahoz-Beltra, 2008; A Balassub-

ramaniam, Memeber, IEEE, P Lio, 2013).

In this paper, we also simulate the bacterial con-

jugation behavior as an information exchange mech-

anism between bacteria in population P and archive

A. To model this biological behavior, we ﬁrst deﬁne

conjugation length L (L < n) measured by the number

of decision variables. Then each bacterium i in pop-

ulation P will randomly select another bacterium i

′

A and a conjugation point Bt (Bt < n − L) to take a

conjugation step. In this step, the way of updating the

solution is given as follows:

new

( j,k,l) = x

( j,k,l) + ω ◦ (x

′

( j,k,l) − x

( j,k,l)),

(9)

where x

new

( j,k,l) denotes the new solution after bac-

terium i performing the conjugation operator. ω is

Multiobjective Bacterial Foraging Optimization using Archive Strategy

187

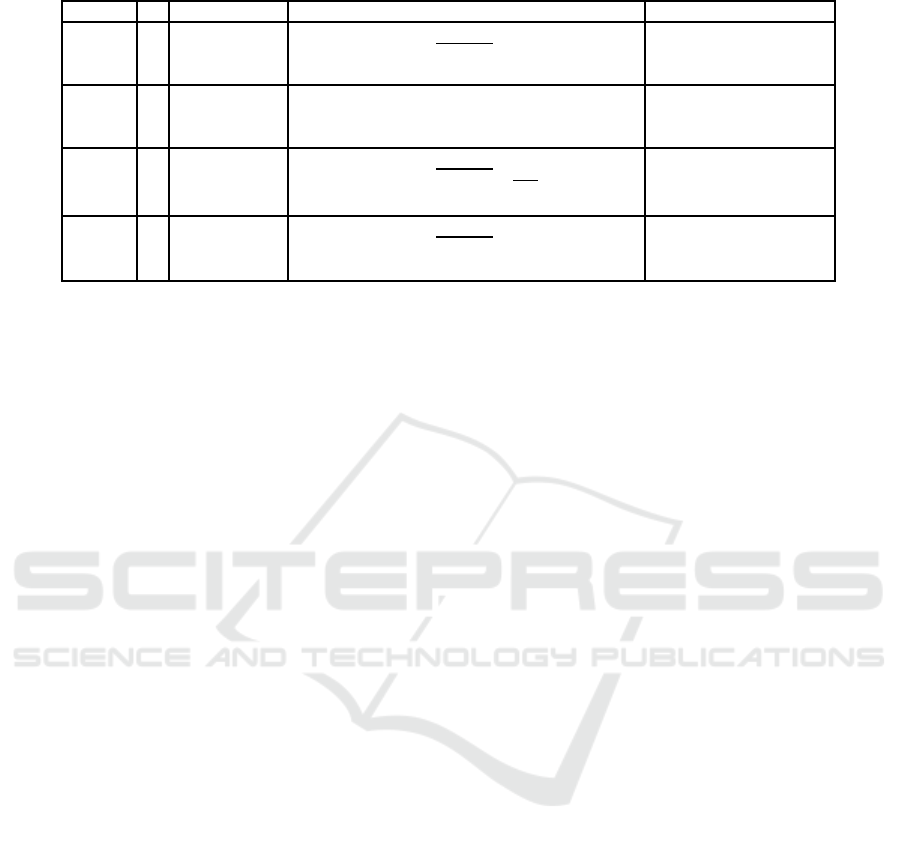
Table 1: Test problems used in this paper.

Problem n Variable range Objective functions Pareto-optimal solutions

ZDT1 30 [0,1] f

(x) = x

∈ [0,1]

(x) = g(x)[1−

/g(x)] x

= 0,i = 2,··· ,n

g(x) = 1+9(

∑

i=2

)/(n−1)

ZDT2 30 [0,1] f

(x) = x

∈ [0,1]

(x) = g(x)[1− (x

/g(x))

] x

= 0,i = 2,··· ,n

g(x) = 1+9(

∑

i=2

)/(n−1)

ZDT3 30 [0,1] f

(x) = x

∈ [0,1]

(x) = g(x)[1−

/g(x) −

g(x)

sin(10πx

)]

= 0,i = 2,··· ,n

g(x) = 1+9(

∑

i=2

)/(n−1)

ZDT4 10 x

∈ [0,1] f

(x) = x

∈ [0,1]

∈ [−5,5], f

(x) = g(x)[1−

/g(x)] x

= 0,i = 2,··· ,n

i = 2, ··· ,n g(x) = 1+ 10(n− 1) +

∑

i=2



− 10cos(4πx

)



a n-dimensional random vector in which the values

of components Bt to Bt + L − 1 are uniformly dis-

tributed random numbers between −1 and 1, and

those of other components are 0. “◦” is an opera-

tor, called Hadamard product, which represents mul-

tiplying the corresponding elements of two vectors.

Take 3-dimensional vectors for an example, if a =

), b = (b

), then D = A ◦ B = (a

× b

). If the new solution x

new

( j,k,l)

is dominated by the old solution x

( j,k,l), x

( j,k,l) is

kept; otherwise, x

new

( j,k,l) replaces x

( j,k,l). With

this communication mechanism, each bacterium in

the population P searches for the nondominated so-

lutions under the guidance of the superior individuals

in the archive A. Thus, the bacterial population are

likely to quickly converge to the global Pareto front.

3.4 Reproduction

The bacteria grow longer with the increasing of the

nutrients absorbed. The more nutrients a bacterium

gets, the healthier it is. Under appropriate conditions,

some of bacteria in a population who are healthy

enough will asexually split into two bacteria, and

the other ones will die. Essentially, the reproduction

mechanism is to generate newpopulation based on the

superior individuals in current population. In the pro-

posed MABFO algorithm, the reproduction operator

selects N1 superior individuals from the joint popu-

lation of the current population P (|P| = N1) and the

external archive A and produces a new population P

by copying these selected N1 superior individuals to

P. The way to select N1 superior individuals is as fol-

lows: ﬁrst sort the joint population of P and A into

different nondominated levels as reference (?) did.

The ﬁrst nondominated level F

contains all the cur-

rent nondominated solutions. Then we pick out solu-

tions in ascending order of the nondominated level to

form a new group R until the size of R would be equal

or larger than N1 if we incorporate the tth nondomi-

nated level F

. In the ﬁrst case, the size of R is exactly

equal to N1 if putting F

into R, just put it into R and

this select step is completed. In the second case, the

size of R is larger than N1 if F

is loaded into R. In

this case, we need to ﬁrst pick out N1 − |R| solutions

from F

based on the crowding distance according to

(8) and then put them into R. In this way, |R| is also

exactly the same with N1. Next, R is used to update

the old population P by copying it to P. Thus, the

new population P which contains the best individuals

is obtained. Such reproduction mechanism follows

the rule of survival of the ﬁttest, which plays a role of

transmitting good information among the whole pop-

ulation and speeding up the convergence.

3.5 Elimination-and-dispersal

With changes to the local environment in which a

population of bacteria lives, all of the bacteria in

this region may be killed, or a group of bacteria

may be dispersed into a new environment to ﬁnd bet-

ter food sources. To simulate this phenomenon, an

elimination-and-dispersal step is taken in BFO after

reproduction steps. Each bacterium in the popula-

tion may be eliminated or dispersed to a new location

with a given probability P

. The rule is shown in the

following:

x =



′

, if r < P

x, otherwise

, (10)

where r is a random number uniformly distributed in

[0,1], x is the current solution associated with a bac-

terium, x

′

is a new solution generated at random in n-

dimension search space. That is, for each bacterium,

if the number generated randomly is smaller than P

it will move to a new random solution, otherwise, it

will keep the original solution unchanged. This mech-

anism is helpful to escape from local Pareto optima

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

188

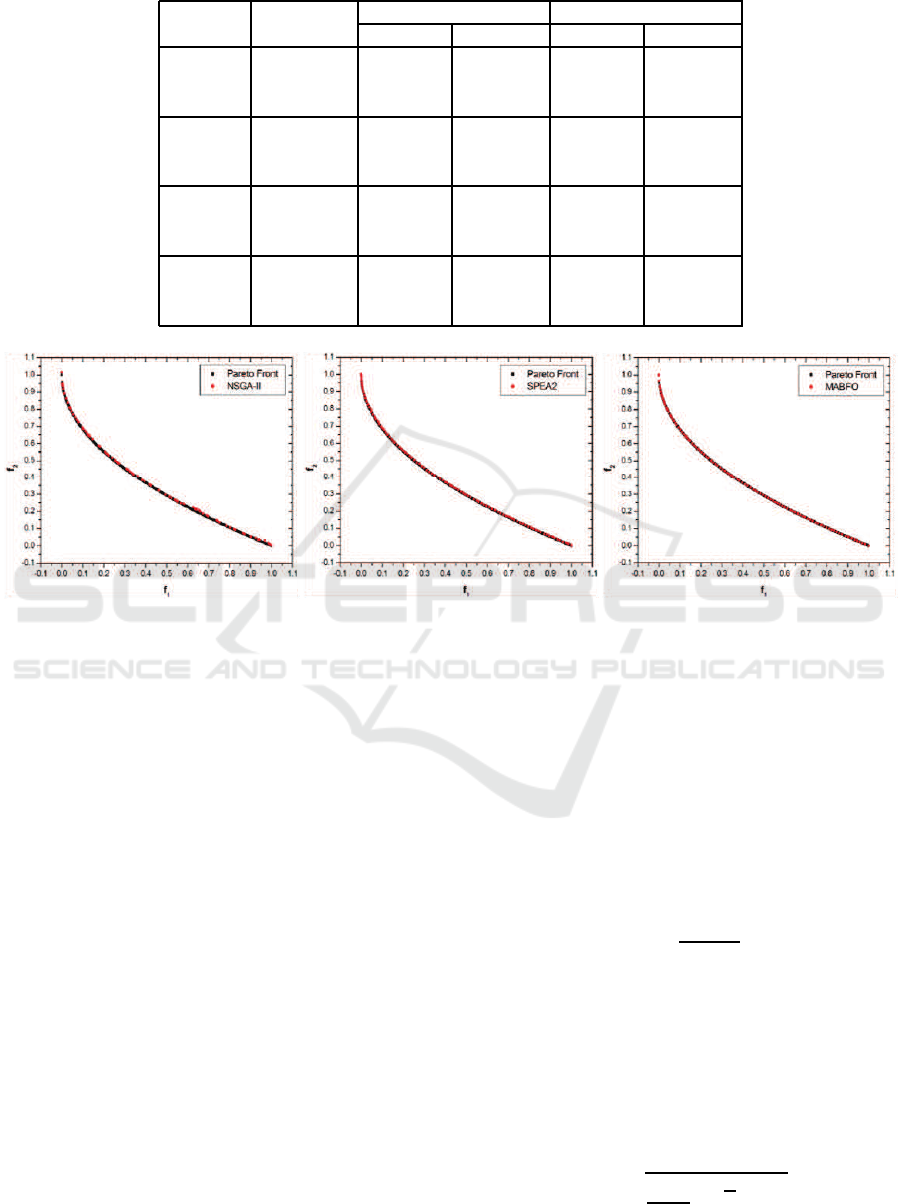
Table 2: Performance comparisons of NSGA-II, SPEA2 and MABFO on four test problems.

Problem Algorithm

GD SP

Average Std. Dev. Average Std. Dev.

NSGA-II 5.10e-04 1.24e-04 9.14e-03 1.13e-03

ZDT1 SPEA2 3.76e-04 6.36e-05 3.28e-03 3.80e-04

MABFO 1.96e-04 4.55e-05 3.24e-03 5.48e-04

NSGA-II 3.66e-04 2.80e-04 1.02e-02 3.09e-03

ZDT2 SPEA2 1.74e-04 2.83e-05 3.15e-03 3.62e-04

MABFO 9.26e-05 4.42e-06 3.04e-03 2.98e-04

NSGA-II 5.22e-04 2.46e-04 1.02e-02 1.50e-03

ZDT3 SPEA2 3.73e-04 1.10e-04 4.42e-03 5.79e-04

MABFO 1.59e-04 1.24e-05 4.85e-03 1.11e-03

NSGA-II 2.45e-03 9.01e-04 1.33e-02 5.07e-03

ZDT4 SPEA2 1.88e-03 7.50e-04 4.17e-03 1.25e-03

MABFO 2.34e-04 2.20e-04 2.40e-03 1.52e-03

Figure 1: Pareto fronts produced by NSGA-II (left), SPEA2 (middle) and MABFO (right) for the ZDT1 test problem.

and to explore the global Pareto optima in the search

space.

4 EXPERIMENTS

In this section, we will compare the proposed

MABFO algorithm with two state-of-the-art algo-

rithms NSGA-II and SPEA2. The experimental plat-

form is a PC with Inter(R) Core(TM) i5- 3470 CPU

3.20GHz, 4GB RAM and Windows 7, and all the al-

gorithms are implemented using C++ language.

4.1 Test Functions and Evaluation

Metrics

We choose four test problems ZDT1, ZDT2, ZDT3

and ZDT4 which are suggested by Zizler and com-

monly used in a number of signiﬁcant past studies.

All the test problems have two objective functions and

have not any constraint. Table 1 lists these test prob-

lems and also provides the number of variables, their

ranges, the Pareto-optimal solutions for each prob-

lem.

In general, there are two issues to consider for as-

sessing a method in multiobjective optimization area:

(1) the convergence of the obtained Pareto front to-

ward the true Pareto front and (2) spread of the ob-

tained solutions. Based on this notion, we adopt two

common metrics: Generational distance (GD) (Van

Veldhuizen D A, Lamont G B, 1998) and Space

(SP) (Schott J R, 1995).

GD measures the distance between the Pareto

front found so far and the true Pareto front. It is de-

ﬁned as:

GD =

∑

i=1

, (11)

where n is the number of members in the Pareto front

found so far, d

is the Euclidean distance between the

ith member of the Pareto front found and the nearest

member of the true Pareto front. The smaller the value

of this metric, the nearer the Pareto front found so far

to the true Pareto front.

SP judges how well the Pareto front found so far

distributed and is formulated as follows:

SP =

n− 1

∑

i=1

(

d − d

)

, (12)

Multiobjective Bacterial Foraging Optimization using Archive Strategy

189

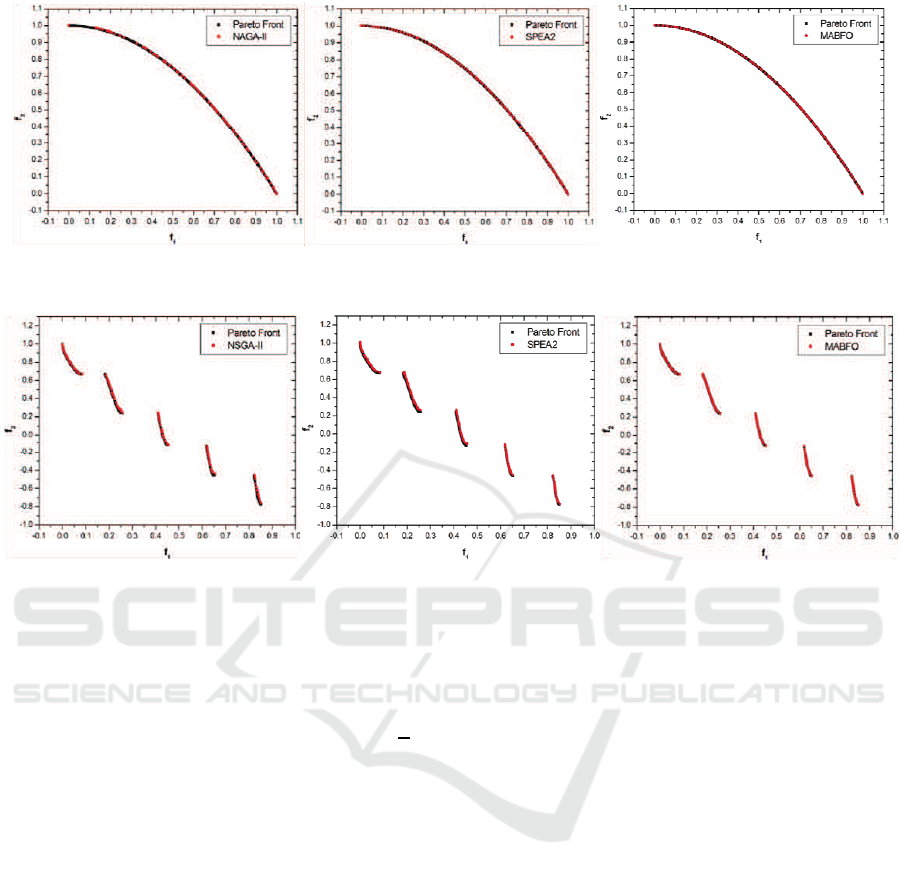
Figure 2: Pareto fronts produced by NSGA-II (left), SPEA2 (middle) and MABFO (right) for the ZDT2 test problem.

Figure 3: Pareto fronts produced by NSGA-II (left), SPEA2 (middle) and MABFO (right) for the ZDT3 test problem.

where n is the number of members in the Pareto

front found so far, d

is the minimum Manhatton dis-

tance between the ith member and other members

in the Pareto front found and d

= min

(| f

) −

)| + | f

) − f

)| + ··· + | f

) − f

)|),

j = 1,2,· ·· ,n. m is the number of the objectives.

d is

the average value of all d

. The smaller the value of

this metric, the more uniform the Pareto front found

is distributed.

4.2 Results and Analysis

In the experiments, each algorithm was tested 30 in-

dependent runs on each test problem. To be fair,

the population sizes and the elite archive sizes of the

three algorithms were set to 100. The generations of

NSGA-II and SPEA2 were set to 500. For the other

parameters in NSGA-II and SPEA2 algorithms, we

tried to use identical settings as suggested in the orig-

inal studies. For the left parameters in the proposed

MABFO algorithm, we didn’t make any serious at-

tempt to ﬁnd the best settings and only chose a reason-

able set of values: N

= 4, N

= 10, N

= 25, N

= 2,

= 0.2 and L = 0.4× n.

Table 2 provides the average results (Average) and

standard deviations (Std. Dev.) with respect to the

two metrics GD and SP. The best average results with

respect to each metric are shown in bold. It can

be seen from the table, the average performance of

MABFO is the best with respect to the GD and SP

metrics on ZDT1, ZDT3 and ZDT4. As for ZDT2,

MABFO achieves the best result in term of GD and is

only slightly worse than SPEA2 in term of SP, but it

has the smallest deviation with respect to SP.

Figures 1-4 show the Pareto fronts obtained by

NSGA-II, SPEA2 and our MABFO algorithm on the

four test problems–ZDT1, ZDT2, ZDT3 and ZDT4,

respectively. The Pareto fronts displayed correspond

to the median results over 30 runs with respect to

the GD metric. From these ﬁgures, we can see

that the three algorithms are able to cover the entire

Pareto fronts on ZDT1, ZDT2 and ZDT3. But our

MABFO algorithm produces better-distributed and

higher-quality Pareto front on these three test prob-

lems, especially on the ZDT3 problem. For the ZDT4

problem, both NSGA-II and SPEA2 fail to cover the

true Pareto front, whereas our MABFO algorithm

successfully does it. Through the comparison with

two best EMO algorithms NSGA-II and SPEA2, our

MABFO algorithm is a viable alternative to solve

MOPs.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

190

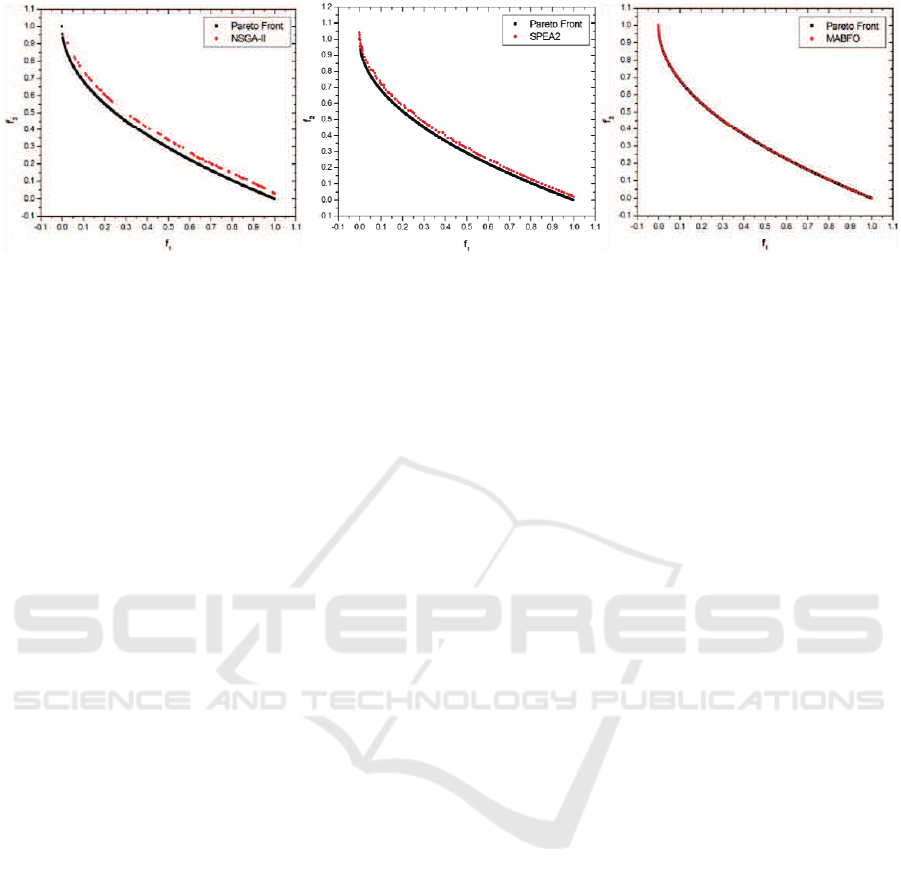
Figure 4: Pareto fronts produced by NSGA-II (left), SPEA2 (middle) and MABFO (right) for the ZDT4 test problem

5 CONCLUSIONS

The MOP is a very important research topic in both

science and engineering communities. In recent

years, researchers are interested in using some new

bio-inspired optimization models to solve MOPs. Al-

though several methods based on BFO have been

proposed for handling MOPs. But to the best of

our knowledge, the current methods based on BFO

havenot incorporated the elitist strategy which always

plays an important role in getting global Pareto front.

In this paper, we present a new algorithm based on

archive bacterial foraging optimization for multiob-

jective optimization (called MABFO). MABFO sim-

ulates four biological mechanisms: chemotaxis, con-

jugation, reproduction and elimination-and-dispersal.

The implements of these mechanisms are different

from other methods based on BFO. More impor-

tant, MABFO incorporates an external archive to

save the nondominated solutions previously found

and maintains the diversity of the nondominated so-

lutions found based on the crowding distance. To

demonstrate the performance of MABFO algorithm,

we compared it with two best methods known to date

(NSGA-II and SPEA2) on four test problems, the re-

sults indicate that MABFO is a promising alternative

since it has the best average performance with respect

to two metrics in most cases.

In the future, we will give an detailed analysis

of the algorithm, make a comprehensive testing on

more test problems and continue to explore more ef-

fective diversity preservation strategies to better cover

the global Pareto front. We also hope to extend this

algorithm so that it can handle dynamic functions.

ACKNOWLEDGEMENTS

This work is partly supported by the NSFC

Research Program (61375059, 61332016), the

National 973 Key Basic Research Program of

China (2014CB744601), Specialized Research Fund

for the Doctoral Program of Higher Education

(20121103110031), and the Beijing Municipal Edu-

cation Research Plan key project (Beijing Municipal

Fund Class B) (KZ201410005004).

REFERENCES

A Balassubramaniam, Memeber, IEEE, P Lio (2013).

Multi-hop conjugation based bacteria nanonetworks.

In IEEE Trans. on Nanobiosci., volume 12, pages 47–

59.

Agrawal V, Sharma H, Bansal J C (2011). Bacterial for-

aging optimization: A survey. In SocProS’2011, Pro-

ceedings of the International Conference on Soft Com-

puting for Problem Solving, pages 227–242, India.

C Perales-Grav´an, R Lahoz-Beltra (2008). An am radio

receiver designed with a genetic algorithm algorithm

based on a bacterial conjugation genetic operator. In

IEEE Trans. Evol. Comput., volume 12, pages 129–

142.

Coello C A C, Pulido G T, Lechuga M S (2004). Handling

multiple objectives with particle swarm optimization.

In IEEE Transactions on Evolutionary Computation,

volume 8, pages 256–279.

Coello Coello CA, Van Veldhuizen DA, Lamont GB (2007).

Evolutionary Algorithms for Solving Multi-Objective

Problems. New York, springer-verlag edition.

Corne D W, Jerram N R, Knowles J D, et al (2001). PESA-

II: Region-based selection in evolutionary multiobjec-

tive optimization. In GECCO’2001, Proceedings of

the Genetic and Evolutionary Computation Confer-

ence, pages 283–290.

Deb (2001). Multi-objective Optimization using Evoulu-

tionary Algorithms. Chichester, john wiley & sons

edition.

Multiobjective Bacterial Foraging Optimization using Archive Strategy

191

Deb K, Pratap A, Agarwal S, et al (2002). A fast and

elitist multiobjective genetic algorithm: NSGA-II.

In IEEE Transactions on Evolutionary Computation,

volume 6, pages 182–197.

E Zitzler, M Laumanns, L Thiele (2002). SPEA2: Improv-

ing the strength pareto evolutionary algorithm. In Evo-

lutionary Methods for Design, Optimization and Con-

trol with Applications to Industrial Problems, pages

95–100, Berlin.

Guzm´an M A, Delgado A, De Carvalho J (2010). A novel

multiobjective optimization algorithm based on bacte-

rial chemotaxis. In Engineering Applications of Arti-

ﬁcial Intelligence, volume 23.

K.M. Passino (2002). Biomimicry of bacterial foraging for

distributed optimization and control. In Control Sys-

tems, volume 22, pages 52–67.

Niu B, Wang H, Tan L, et al (2012). Multi-objective opti-

mization using bfo algorithm. In Bio-Inspired Com-

puting and Applications, pages 582–587.

Niu B, Wang H, Wang J, et al (2013). Multi-objective bac-

terial foraging optimization. In Neurocomputing, vol-

ume 116, pages 336–345.

Panigrahi B K, Pandi V R, Das S, et al (2010). Multiobjec-

tive fuzzy dominance based bacterial foraging algo-

rithm to solve economic emission dispatch problem.

In Energy, volume 35, pages 227–242.

Parks G T, Miller I (1998). Selective breeding in a multiob-

jective genetic algorithm. In Parallel Problem Solving

From NaturełPPSN V, pages 250–259.

S Dasgipta, S Das, A Abraham and A Biswas (2009). Adap-

tive computational chemotaxis in bacterial foraging

optimiztion: An analysis. In IEEE Transactions on

Evolutionary Computation, volume 13, pages 919–

941.

Schott J R (1995). Fault tolerant design using single and

multicriteria genetic algorithm optimization. In MS

Thesis, Massachusetts institute of Technology, Cam-

bridge.

Tripathi P K, Bandyopadhyay S, Pal S K (2007). Multi-

objective particle swarm optimization with time vari-

ant inertia and acceleration coefﬁcients. In Informa-

tion Sciences, volume 177, pages 5033–5049.

Van Veldhuizen D A, Lamont G B (1998). Multiobjec-

tive evolutionary algorithm research: A history and

analysis. In Technical Report TR-98-03, Department

of Electrical and Computer Engineering, Graduate

School of Engineering, Air Force Institute of Technol-

ogy, Ohio.

X Li (2003). A non-dominated sorting particle swarm

optimizer for multiobjective optimization. In

GECCO’2003, Proceedings of Genetic and Evolu-

tionary Computation, pages 37–48.

Zitzler E, Deb K, Thiele L (2000). Comparison of multiob-

jective evolutionary algorithms: Empirical results. In

Evolutionary computation, volume 8, pages 173–195.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

192