
A Practical-time Attack on Reduced-round MISTY1
Nobuyuki Sugio
1
, Yasutaka Igarashi
2
, Toshinobu Kaneko
2
and Kenichi Higuchi
2
1
NTT DOCOMO, INC., 3-6 Hikarinooka, Yokosuka, Kanagawa, 239-8536, Japan
2
Tokyo University of Science,2641 Yamazaki, Noda, Chiba, 278-8510, Japan
Keywords:
MISTY1, Symmetric Key Algorithm, Block Cipher, Higher Order Differential Attack.
Abstract:
MISTY1 is a symmetric key algorithm which has been standardized by ISO and that its modified version is
used in GSM and 3G mobile networks. MISTY1 is a 64-bit block cipher supporting key length of 128 bits. In
this paper, we focused on evaluating the security of MISTY1 against higher order differential attack. We show
6-round MISTY1 with 4 FL layers is attackable with 2
43
blocks of chosen plaintexts and 2
43.31
times of data
encryption. This is the best practical-time attack on reduced-round MISTY1.
1 INTRODUCTION
MISTY1 is one of the symmetric key algorithms.
MISTY1 is a 64-bit block cipher supporting key
length of 128 bits. MISTY1 was proposed by Mat-
sui in 1997 (Matsui, 1997). The number of rounds is
8. MISTY1 achieves a provable security against dif-
ferential cryptanalysis and linear cryptanalysis with
round function FO. Designer adds on an auxiliary
function FL in order to become secure against other
attacks. MISTY1 was selected as one of the NESSIE-
recommended ciphers portfolio and was adopted as
the international standard by ISO/IEC 18033-3 (ISO,
2010). CRYPTREC project has chosen MISTY1 as
one of the e-Government Recommended candidate ci-
phers in 2013 (CRYPTREC, 2013). Furthermore, the
block cipher KASUMI designed as a slight modifica-
tion of MISTY1 is used in the GSM/3G mobile net-
works, which makes it one of the most widely used
block ciphers today.
Up to now, many cryptanalytic methods were used
to evaluate the security of MISTY1 such as higher or-
der differential attack, impossible differential attack,
integral attack, and multi-dimensional zero correla-
tion linear attack. The main previous attacks are as
follows. Tsunoo et. al. proposed 46-th order differ-
ential and showed 7-round MISTY1 with 4 FL lay-
ers was attackable with 2
54.1
chosen plaintexts and
2
120.7
encryptions (Y. Tsunoo and Kawabata, 2008).
Jia et. al. constructed a 7-round impossible differ-
ential and mounted impossible differential attack on
7-round MISTY1 with 3 FL layers (Jia and Li, 2012).
Yi presented zero-correlation linear attack on 7-round
MISTY1 with 4 FL layers, that requires 2
62.9
known
plaintexts and 2
118
encryptions (Yi and Chen, 2014).
Todo introduced Integral attack by division property,
and showed that the secret key of the full MISTY1 can
be recovered with 2
63.58
chosen plaintexts and 2
121
time complexity (Todo, 2015). Bar On improved the
attack proposed by Todo, and presented full MISTY1
was attackable with 2
64
chosen plaintexts and 2
69.5
encryptions (Bar-On, 2015a).
Most of the previous attacks aimed at maximiz-
ing the number of attacked rounds, and as a result,
their complexities are highly impractical. In this pa-
per, we focused on evaluating the security of MISTY1
in terms of practical-time complexity. The previous
practical-time attack was proposed by Hatano et. al.
(Y. Hatano and Kaneko, 2004), and Dunkelman et. al.
(Dunkelman and Keller, 2013), respectively. The best
practical-time attack was higher order differential at-
tack on 5-round MISTY1 with 4 FL layers.The neces-
sary computational complexity by using higher order
differential can be estimated as sum of the following
2-steps.
1. Preparation of data
2. Key recovery
The order of differential affects both steps. Therefore,
it is very important to discover the lower order differ-
ential characteristics to reduce the complexity for an
attack. The results we obtain are the following.
1. We implemented the 46th-order differential for
4-round MISTY1 introduced in (Y. Tsunoo and
Kawabata, 2008) on a computer which mounted
Graphics Processing Unit (GPU) co-processors
Sugio, N., Igarashi, Y., Kaneko, T. and Higuchi, K.
A Practical-time Attack on Reduced-round MISTY1.
DOI: 10.5220/0005652202350242
In Proceedings of the 2nd International Conference on Information Systems Security and Privacy (ICISSP 2016), pages 235-242
ISBN: 978-989-758-167-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
235

Table 1: Summary of single-key attacks on MISTY1.
Rounds FL layers Data Time Attack algorithm Reference
5 4 2
22
CP 2
28
Higher Order Differential (Y. Hatano and Kaneko, 2004)
6 4 2
51
CP 2
123.4
Impossible Differential (Dunkelman and Keller, 2008)
6 4 2
53.7
CP 2
53.7
Higher Order Differential (Y. Tsunoo and Kawabata, 2008)
6 4 2
43
CP 2
43.31
Higher Order Differential Section5
7 0 2
50.2
KP 2
114.1
Impossible Differential (Dunkelman and Keller, 2008)
7 3 2
58
KP 2
124.4
Impossible Differential (Jia and Li, 2012)
7 4 2
62.9
KP 2
118
Multi-Zero Correlation (Yi and Chen, 2014)
7 4 2
54.1
CP 2
120.7
Higher Order Differential (Y. Tsunoo and Kawabata, 2008)
7 5 2
51.45
CP 2
121
Higher Order Differential (Bar-On, 2015b)
8 5 2
63.58
CP 2
121
Integral by division property (Todo, 2015)
8 5 2
64
CP 2
69.5
Integral by division property (Bar-On, 2015a)
CP: Chosen Plaintexts, KP : Known Plaintexts.
Table 2: The Key Scheduling of MISTY1.
KO
i1
KO
i2
KO
i3
KO
i4
KI
i1
KI
i2
KI
i3
KL
i1
KL
i2
K
i
K
i+2
K
i+7
K
i+4
K
0
i+5
K
0
i+1
K
0
i+3
K
i+1
2
(odd i) K
0
i+1
2
+6
(odd i)
K
0
i
2
+2
(even i) K
i
2
+4
(even i)
and found 16-bits of the above characteristic was
always 0. We gradually reduced the order of dif-
ferentials for 4-round MISTY1 by computer ex-
periment, and discovered new 38-th order differ-
ential characteristics for 4-round MISTY1 which
held 7-bits of those differential characteristics 0
1
.
2. We can attack 6-round MISTY1 with 4 FL layers
by using the 38-th order differential characteris-
tic. The complexity for the attack needs 2
43
cho-
sen plaintexts and 2
43.31
encryptions. Our method
can reduce the necessary number of chosen plain-
texts and the computational cost for the attack of
6-round MISTY1 with 4 FL layers illustrated in
(Y. Tsunoo and Kawabata, 2008) by a factor of
2
10
. This is the best practical-time attack on 6-
round MISTY1. Summary of main attacks on
MISTY1 are shown in Table 1.
The remainder of this paper is organized as fol-
lows. Section 2 gives a brief introduction of MISTY1.
Section 3 explains higher order differentials and its
application for an attack. Section 4 shows previous
higher order differentials and presents a new higher
order differential for 4-round MISTY1. Section 5
proposes higher order differential attack on 6-round
MISTY1 with 4 FL layers. Section 6 summarizes this
paper.
1
The characteristic of 38-th order differential equals to
the characteristic of 46-th order differential for 4-round
MISTY1 estimated in (Y. Tsunoo and Kawabata, 2008)
2 MISTY1
MISTY1 is a Feistel type 64-bit block cipher support-
ing secret key length of 128 bits. MISTY1 was pro-
posed by Matsui in 1997 (Matsui, 1997). The number
of rounds which designer recommends is 8. MISTY1
achieves a provable security against differential crypt-
analysis and linear cryptanalysis with round function
FO. Designer adds on an auxiliary function FL in or-
der to become secure against other attacks.
Figure 1 shows the main structure and components
of the cipher. The round function FO
i
(1 ≤ i ≤ 8) is
a variant of a 3-round Feistel construction which has
16-bit bijective function FI
i j
(1 ≤ j ≤ 3) and 16-bit
extended key KO
i j
(1 ≤ j ≤ 4), KI
i j
(1 ≤ j ≤ 3). FI
i j
is a variant of a 3-round Feistel construction and its in-
put is divided into left 9-bit data and right 7-bit data,
which are transformed by bitwise XOR operations de-
noted by the symbol ⊕ and substitution tables S7 and
S9. KI
i j1
and KI
i j2
are left 7-bit data and right 9-bit
data of KI
i j
, respectively. The key dependent linear
function FL
i
are composed of bitwise AND operation
denoted by the symbol ∩, OR operation denoted by
the symbol ∪, XOR operations and KL
i j
(1 ≤ j ≤ 2).
The key schedule of MISTY1 takes the 128-bit se-
cret key K to generate extended keys. Let K
i
(1 ≤ i ≤
8) be the i-th (from left) 16-bit data of the secret key
K, and let KO
i
(1 ≤ i ≤ 8) be the output of FI
i j
where
the input of FI
i j
is K
i
and the key KI
i j
is K
i+1
. Also,
identify K
9
with K
1
. The correspondence between the
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
236
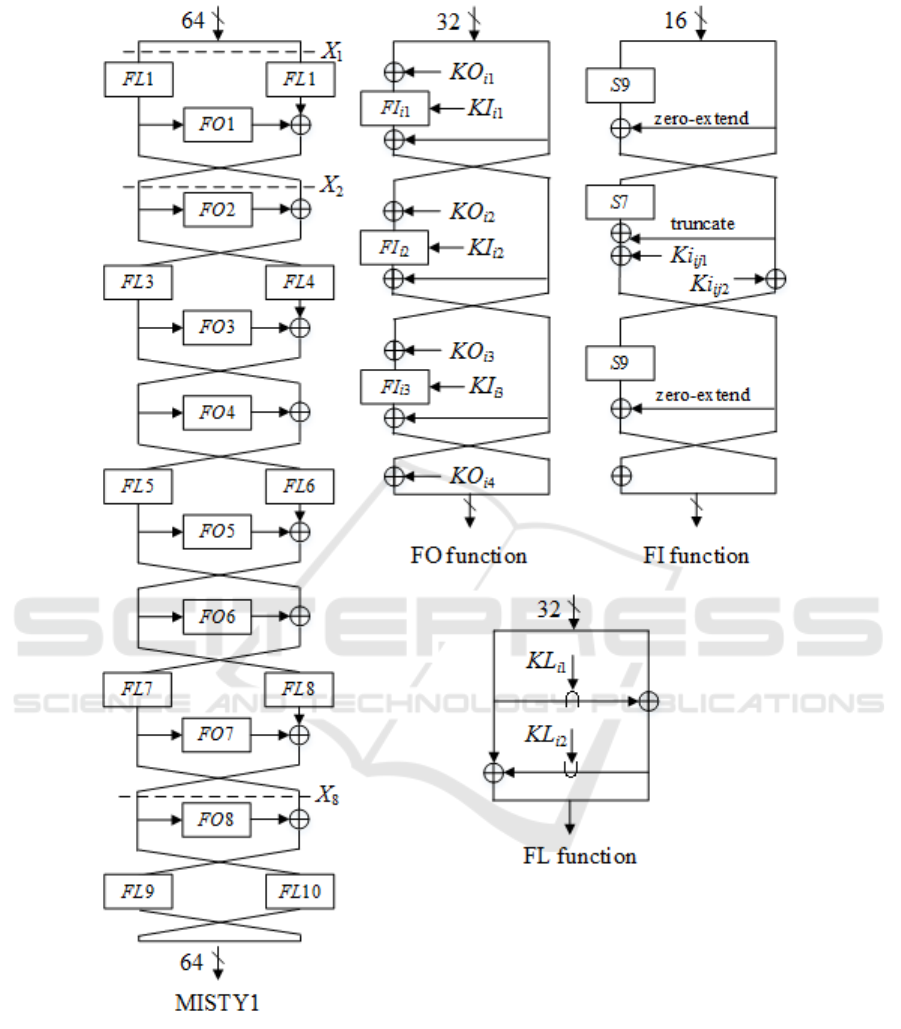
Figure 1: Outline of MISTY1.
symbols KO
i j
, KI
i j
, KL
i j
and the actual key is shown
in Table 2. Here, K
0
i
is the output of FI
i, j
where the
input is K
i
and the key is K
i+1
.
2.1 Notations Used in This Paper
We use the following notations for intermediate val-
ues during the MISTY1 encryptions process.
• The plaintext and ciphertext are denoted by P and
C. The left 32-bit value of P is denoted by P
L
and
the right 32-bit value of P is denoted by P
R
. The
left 32-bit value of C is denoted by C
L
and the
right 32-bit value of C is denoted by C
R
, respec-
tively.
• The input of i-th round (1 ≤ i ≤ 8) are denoted by
X
i
. We denote the intermediate value after appli-
A Practical-time Attack on Reduced-round MISTY1
237

cation of FL functions by X
0
i
.
• Let Z be a intermediate variable. Z[k] denotes k-th
bit of Z and Z[k − l] denotes bits from k to l of Z
respectively.
3 HIGHER ORDER
DIFFERENTIAL ATTACK
This section gives an overview of higher order differ-
ential attack.
3.1 Higher Order Differential (Lai,
1994)
Let E(·) be an encryption function as follows.
Y = E(X;K) (1)
where X ∈ GF(2)
n
, K ∈ GF(2)
s
, Y ∈ GF(2)
m
. For a
block cipher, X, K and Y denote plaintext, key and
ciphertext respectively. Let {a
1
,a
2
,· ·· ,a
i
} be a set
of linearly independent vectors in GF(2)
n
and V
(i)
be a sub-space spanned by these vectors. We define
∆
(i)
V
(i)
E(X; K) as an i-th order differential of E(X; K)
with respect to X as follows.
∆
(i)
V
(i)
E(X; K) =
M
A∈V
(i)
E(X ⊕ A; K) (2)
In the following, we abbreviate ∆
(i)
V
(i)
as ∆
(i)
, when
it is clearly understood. In this paper, we use the
following properties of the higher order differential.
Property 1. If the degree of E(X; K) with re-
spect to X equals to d, then
deg
X
{E(X; K)} = d ⇔
∆
(d+1)
E(X; K) = 0
∆
(d)
E(X; K) = const
(3)
Property 2. Higher order differential has a linear
property on XOR sum. That means d-th order differ-
ential of the sum of each function equals to the sum
of d-th order differential of each function.
∆
(d)
{E(X
1
;K
1
) ⊕ E(X
2
;K
2
)} =
∆
(d)
E(X
1
;K
1
) ⊕ ∆
(d)
E(X
2
;K
2
)
(4)
3.2 Attack Equation
Consider an R-round iterative block cipher. Let
H
R−1
(X) ∈ GF(2)
m
be a part of the (R − 1)-th round
output and C(X) ∈ GF(2)
n
be the ciphertext corre-
sponding to the plaintext X ∈ GF(2)
n
. H
R−1
(X) is
expressed as follows.
H
R−1
(X) = F
R−1
(·· ·F
2
((F
1
(X;K
1
);K
2
),· ·· ,K
R−1
)
(5)
where K
i
∈ GF(2)
s
be the i-th round key and F(·) be
a function of GF(2)
n
× GF(2)
s
→ GF(2)
m
.
If the degree of H
R−1
(X) with respect to X is d,
we have the following equation from Property 1.
∆
(d+1)
H
R−1
(X) = 0 (6)
This equation holds with probability 1.
Let
˜
F(·) be a decoding function that calculates
H
R−1
(X) from a ciphertext C(X ) ∈ GF(2)
n
.
H
R−1
(X) =
˜
F(C(X); K
R
) (7)
where K
R
∈ GF(2)
s
denotes the R-th round key to de-
code H
R−1
(X) from C(X). From equation (6), (7) and
(2), we can derive following equation.
M
A∈V
(d+1)
˜
F(C(X ⊕ A); K
R
) = 0 (8)
We can determine K
R
by solving (8). In the following,
we refer to equation (8) as an attack equation for key
recovery.
3.3 Algebraic Method
Shimoyama et al. proposed an effective method
of solving equation (8) (T. Shimoyama and Tsujii,
1999). This method, called algebraic method in this
paper, expands equation (8) as boolean polynomials
over GF(2), and linearizes by treating every higher or-
der variables like k
i
k
j
with new independent variables
like k
i j
. In the following, we use the term linearized
attack equation to refer to an attack equation that is
regarded as a linear equation.
Let L be the number of unknowns in the linearized
attack equation (8). Since the equation (8) is derived
by using an m-bit sub-block, we can rewrite equation
(8) as follows.
Ak = b , k =
t
(k
1
,k
2
,. ..,k
1
k
2
,. ..,k
1
k
2
k
3
,· ·· ) (9)
where A, b, and k are the m ×L coefficient matrix, the
m-dimensional vector, and the L-dimensional vector
over GF(2). k denotes linearized unknowns that are
expressed as monomials of the R-th round key K
R
.
We can obtain m linearized attack equations from
one (d + 1)-th order differential because equation (8)
is an m-bit equation. Therefore we need
d
L/m
e
sets
of the (d + 1)-th order differential for the unique so-
lution.
Since one set of (d + 1)-th order differential re-
quires 2
d+1
chosen plaintexts, the necessary number
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
238

of plaintexts D for the determination of a key is esti-
mated as
D = 2
d+1
×
L
m
(10)
If we use the same technique shown in (T. Shimoyama
and Tsujii, 1999), equation (9) requires 2
d+1
×(L+1)
times of
˜
F(·) calculations. Since we have to prepare
d
L/m
e
sets of (d + 1)-th order differentials to deter-
mine k, the computational cost
2
is estimated as
T = 2
d+1
× (L + 1) ×
L
m
(11)
Hatano et. al. proposed the optimization for al-
gebraic method by analyzing the number of indepen-
dent unknowns l(≤ L) in equation (8) (Y. Hatano
and Kaneko, 2004). If we can analyze the num-
ber of independent unknowns l(≤ L) in equation (8),
the
d
l/m
e
× l coefficient matrix A
op
and the
d
l/m
e
-
dimensional vector b
op
is sufficient for solving the
linearized attack equation.
4 HIGHER ORDER
DIFFERENTIALS FOR
REDUCED ROUND MISTY1
This section explains the previous results of higher
order differential characteristic of MISTY1 and il-
lustrates new higher order differential characteris-
tics which we discovered. Here, α and β denote
fixed and variable sub-block respectively. For ex-
ample, 64-bit variable Y consisting of a 3-bit vari-
ables a-th, b-th, and c-th bit of sub-block β (0 ≤
a,b, c ≤ 63, a 6= b 6= c) can be denoted as Y =
{
Y [i] ∈ α, Y [ j] ∈ β | i 6= j, j = a,b,c, a 6= b 6= c
}
. A
3-rd order differential of intermediate variable Z[k −l]
by using Y can be denoted as
Y =
{
Y [i] ∈ α, Y [ j] ∈ β | i 6= j, j = a,b,c,a 6=b 6= c
}
∆
(3)
V
(3)
Z[k − l]
(12)
where 0 ≤ i, j,k,l ≤ 63 and V
(3)
is a subspace based
on variable sub-block Y [ j].
4.1 Previous Results
Hatano et. al. proposed 14-th order differential of
3-round MISTY1 with FL functions (Y. Hatano and
2
This computational cost ignores the complexity of
solving linearized attack equation, because the computa-
tional cost is negligible as long as coefficient matrix size
is small.
Kaneko, 2004).
P = {P[i] ∈ α, P[ j] ∈ β | i 6= j, 0 ≤ j ≤ 6,
16 ≤ j ≤ 22}
∆
(14)
V
(14)
X
4
[63 − 57] = 0
(13)
where V
(14)
is the subspace based on variable sub-
block P[22 − 16, 6 − 0].
Tsunoo et. al. proposed 46-th order differential
which was a 1-round extension of the 14-th order
differential to the direction to plaintext. Due to the
Feistel structure of MISTY1, the 3-round 14-th order
differential can be extended to a 4-round 46-th order
differential by taking all the 2
32
possible values in the
previous round. Thus, the following theorem could
be derived.
Theorem. For four consecutive rounds of MISTY1
with FL functions that starts at 1-st round, the
following equation independently holds under
any fixed value of the key, constant value of the
P[i] (39 ≤ i ≤ 47, 55 ≤ i ≤ 63) and V
(46)
is the
subspace based on variable sub-blockP
R
, P[ j]
( 32 ≤ j ≤ 38, 48 ≤ j ≤ 54).
P = {P[i] ∈ α, P[ j], P
R
∈ β | 39 ≤ i ≤ 47,
55 ≤ i ≤ 63, 32 ≤ j ≤ 38, 48 ≤ j ≤ 54}
∆
(46)
V
(46)
X
5
[63 − 57] = 0
(14)
4.2 New Higher Order Differentials for
MISTY1
In this subsection, we describe the new higher order
differential characteristics for MISTY1 which were
discovered by computer experiment.
46-th Order Differential Characteristic. We
implemented 46-th order differential described in
equation (14) on a computer which mounts Graphics
Processing Unit (GPU) co-processors and found the
following 46-th order differential characteristic.
∆
(46)
V
(46)
X
5
[63 − 48] = 0 (15)
Although we verified equation (15) with 10 different
keys and fixed sub-blocks, equation (15) always
held. Since the provability of 10 sets 16-bit random
variables incidentally becomes 0 is 2
−160
, we don’t
think equation (15) accidentally holds.
38-th Order Differential Characteristic. We
gradually reduced the order of differentials in
equation (15) and discovered the new higher order
A Practical-time Attack on Reduced-round MISTY1
239
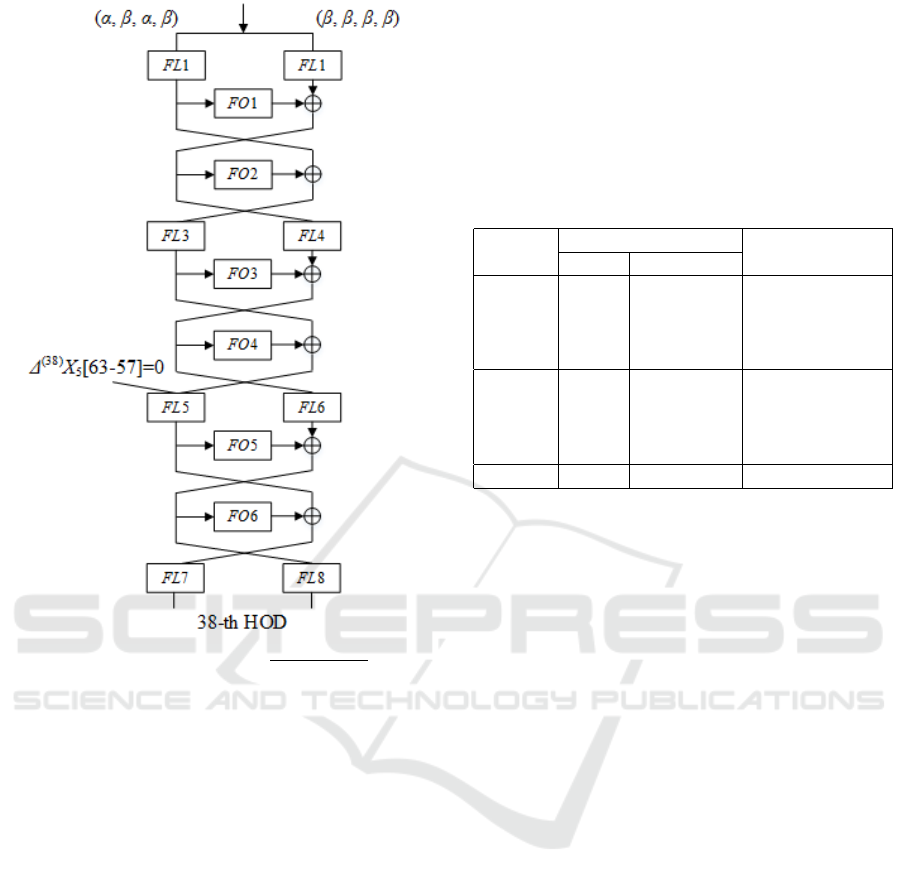
β shown in 32-bit state (α, β, α, β) are 3-bits variables out of
7-bits sub-blocks, respectively.
Figure 2: A new 38th order differential of MISTY1.
differential characteristics as follows.
P = {P[i] ∈ α,P[ j,k],P
R
∈ β | i 6= j, i 6= k
32 ≤ i ≤ 63, j = k + 16,
k = h
1
,h
2
,h
3
(32 ≤ h
1
< h
2
< h
3
≤ 38)}
∆
(38)
V
(38)
X
5
[63 − 57] = 0
(16)
where h
1
, h
2
and h
3
are bit patterns of variable
sub-block. The variations of 38-th order differential
illustrated in equation (16) exist
7
3
=35 patterns.
Other Characteristics. We searched for the new
higher order differential characteristics on 3-round, 4-
round and 5-round MISTY1 respectively. The results
are presented in Table 3.
5 38-TH ORDER DIFFERENTIAL
ATTACK ON REDUCED ROUND
MISTY1
In this section we apply 38-th order differential char-
acteristic to attack 6-round MISTY1 with 4 FL layers.
Table 3: The results of higher order differential characteris-
tics on MISTY1.
We abbreviate ∆
(i)
V
(i)
X
4
[63 − 57] = 0 (i = 7,14) as X
4
[63 − 57] = 0
in the table. This abbreviation is same other characteristics. The
symbol ’N/A’ means that we couldn’t find a higher order diffe-
rential characteristic which satisfied ∆
(i)
V
(i)
X
4
[63 − 41] = 0
(1 ≤ i ≤ 31). (*1) is discovered by Hatano (Y. Hatano and
Kaneko, 2004). (*2)is discovered by Tanaka (H. Tanaka and
Kaneko, 1999). (*3)is discovered by Igarashi (Igarashi and
Kaneko, 2008).
Rounds i-th order diff. Output
FL without FL
3 14
(∗1)
7
(∗2)
X
4
[63 − 57] = 0
3 18 10 X
4
[63 − 48] = 0
3 N/A 26 X
4
[63 − 41] = 0
3 32 31 X
4
[63 − 32] = 0
4 38 32
(∗3)
X
5
[63 − 57] = 0
4 44 36 X
5
[63 − 48] = 0
4 50 47 X
5
[63 − 41] = 0
4 - 48 X
5
[63 − 32] = 0
5 - ∼53 Unknown
We estimate the complexity for an attack by means of
same procedure described in (Y. Tsunoo and Kawa-
bata, 2008). Using the chosen plaintext denoted in
equation (16), we have the following attack equation
by assuming KL
52
[15 − 9] = 0x7 f . (See figure 3.)
M
A∈V
(38)
{FO
6
(X
6
[63 − 32]; KO
61
,KO
62
)[31 − 25]⊕
FL
−1
7
(C
L
(X ⊕A);KL
72
)[31 − 25]} = 0,
X
6
[63 − 32] = FL
−1
8
(C
R
(X ⊕A);KL
81
,KL
82
)
where FL
−1
means an inverse function of FL. We di-
vide the attack equation into seven kinds of 1-bit at-
tack equations in order to increase the success prob-
ability. Assuming KL
52
[15 − 9] = 0x7 f , the seven
kinds of 1-bit attack equations are written as
M
A∈V
(38)
{FO
6
(X
6
[63 − 32]; KO
61
,KO
62
)[i] ⊕
FL
−1
7
(C
L
(X ⊕A);KL
72
)[i]} = 0,
X
6
[63 − 32] = FL
−1
8
(C
R
(X ⊕A);KL
81
,KL
82
)
(17)
where 25 ≤ i ≤ 31. Each 1-bit attack equation holds
with probability 2
−1
. Using those equations, we can
determine the key with probability 1 − 2
−7
, which
means KL
52
[15 − 9] 6= 0x00. Otherwise we can de-
termine KL
52
[15 − 9] = 0x00.
After linearization of the attack equation which
consists of 7-bits width, we obtain the total number
of unknown variables L = 1665 in a system of lin-
ear equations. If any of the unknown variables have
linear sum relations, the complexity for attack can
be reduced. In this paper, we chose independent un-
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
240
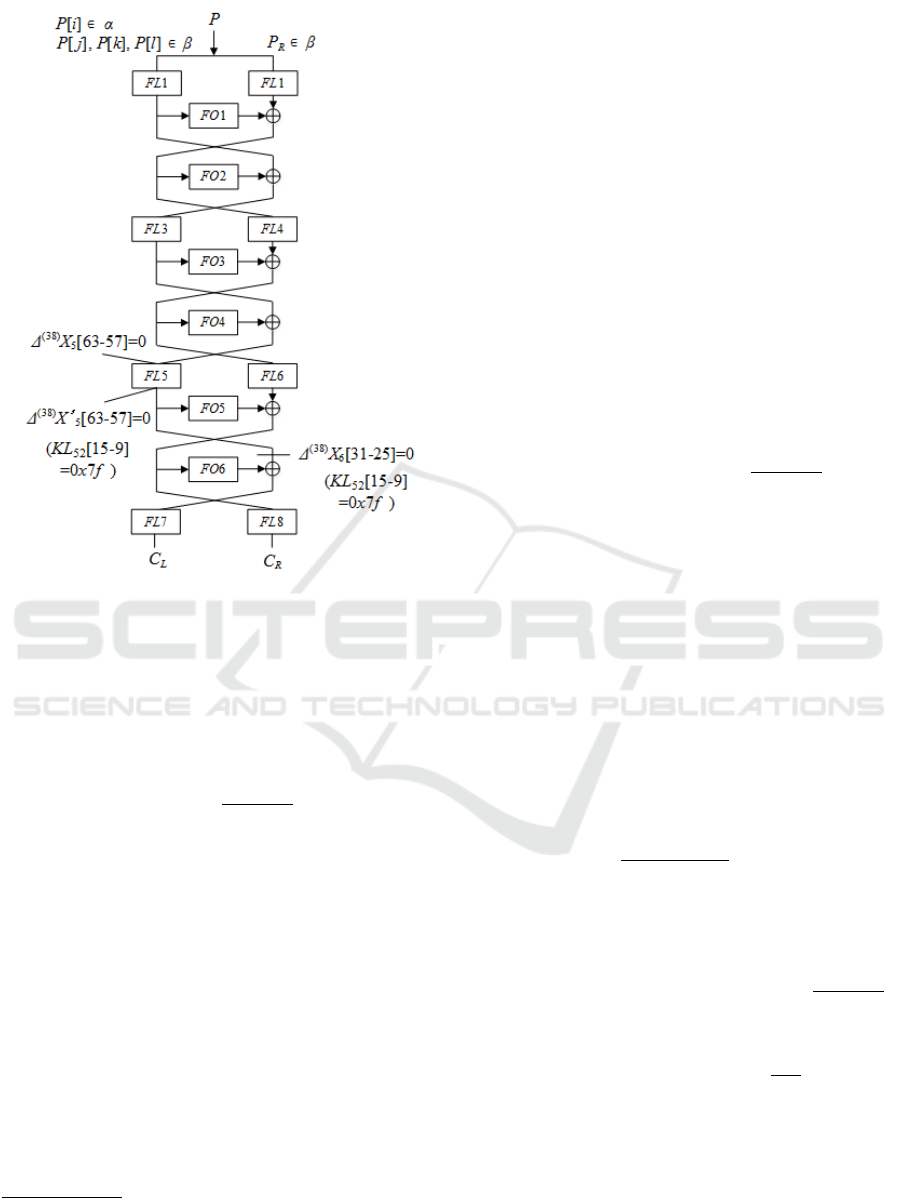
Figure 3: An attack on 6-round MISTY1 by using 38-th
order differential.
known variables
3
l = 189 as worst-case. Because ev-
ery linearized attack equation was derived by 1-bit
key KL
52
[i] assumption, additional 10 linear equa-
tions are needed to remove all false keys. From equa-
tion (10), the necessary number of chosen plaintexts
D is estimated as
D = 2
38
×
189 + 10
m
where m = 1 since the attack solves equation (17) for
each bit. Namely, D = 2
38
× 199 ≈ 2
45.7
. Here, we
can reduce the number of plaintexts D as follows. Let
us consider a 43-rd order differential denoted equa-
tion (18).
P =
{
P[i] ∈ α,P[ j,k,l], P
R
∈ β | i 6= j, k, l, j =k+16
}
k = h
1
,∼, h
5
(32 ≤ h
1
< h
2
< h
3
< h
4
< h
5
≤ 38)
l = h
6
(32 ≤ h
6
≤ 38, or 48 ≤ h
6
≤ 54)
(18)
A 43-rd order differential described in equation (18)
can be used to construct 2
5
×
5
3
=320 sets of 38-th or-
der differential. The explanation is as follows. The
combination of choosing variable bit sub-blocks of
38-th order differential in equation (18) is
5
3
, be-
cause we have to choose 3-bits from (h
1
,∼, h
5
) as
3
It should be noted that the number of independent un-
known variables depends on the exact bit in attack equation.
See (Y. Tsunoo and Kawabata, 2008) in detail.
variable bit sub-blocks. When we regard one set of
43-rd order differential as some sets of 38-th order
differential, the number of fixed bit sub-blocks in 43-
rd order differential is five. 5-bits pattern includes 2
5
possible values. Thus, a 43-rd order differential illus-
trated in equation (18) generates 2
5
×
5
3
=320 > 199
sets of 38-th order differential. Therefore, the neces-
sary number of chosen plaintexts D for key recovery
is estimated as 2
43
.
Now, we consider the time complexity for this at-
tack. The necessary computational cost for an attack
can be estimated as sum of the following 2-steps.
1. Preparation of ciphertexts
2. Key recovery
The time complexity for a preparation of ciphertexts
T
C
is estimated as 2
43
6-round MISTY1 encryptions.
From equation (11), the complexity for key recovery
is estimated as follows.
T
M
= 2
38
× (1665 + 1) ×
189 + 10
1
We can reduce the complexity by using a modulo 2
frequency distribution table. This table counts cipher-
text values appearing an odd number of times since
performing an XOR operation on the same value an
even number of times results in a value of 0. We pre-
pare 2 kinds of tables whose size are 2
18
with respect
to 18-bits C
L
[32 − 23,15 − 7] for 2 S9-boxes and 2
14
with respect to 14-bits C
L
[22 − 16, 6 − 0] for 2 S7-
boxes respectively. The cost for generating these ta-
bles is
T
t
= 2
38
× 2 × 199
table look-ups. If the computational cost for one table
look-up equals to the cost for a S7, S9 look-up, T
t
is
estimated as
T
t
=
2
38
× 2 × 199
6 × 9
≈ 2
40.9
encryptions because 6-round MISTY1 has 6 × 9 S-
boxes. The computational cost from equation (11) by
using these tables is estimated as
T
0
M
= (2 × 2
18
+ 2 × 2
14
) × (1665 + 1) ×
189 + 10
1
≈ 2
37.5
S-box look-ups. T
0
M
is estimated as
2
37.5
6×9
≈ 2
31.8
en-
cryptions. The complexity for solving a system of
equations resulting from linearization is negligible.
The overall time complexity T is estimated as
T = T
C
+ T
t
+ T
0
M
= 2
43
+ 2
40.9
+ 2
31.8
≈ 2
43.31
times of 6-round MISTY1 encryptions. The time
complexity T is dominated by the encryption of plain-
texts.
A Practical-time Attack on Reduced-round MISTY1
241

6 CONCLUSIONS
In this paper, we focused on evaluating the security of
MISTY1 in terms of practical-time complexity. We
implemented the 46th-order differential characteris-
tic for 4-round MISTY1 introduced in (Y. Tsunoo
and Kawabata, 2008) on a computer which mounts
GPU co-processors. We found 16-bits of 46-th order
differential characteristic was 0. We discovered the
new 38-th order differential characteristic for 4-round
MISTY1 whose characteristic is equal to the charac-
teristic estimated in (Y. Tsunoo and Kawabata, 2008).
We applied the 38-th order differential character-
istic to attack 6-round MISTY1 with 4 FL layers. The
complexity for attack needs 2
43
chosen plaintexts and
2
43.31
encryptions. By using 38-th order differential,
we can reduce the necessary number of data and time
complexity for an attack on 6-round MISTY1 with 4
FL layers by a factor of 2
10
. This is the best practical-
time attack on 6-round MISTY1.
REFERENCES
Bar-On, A. (2015a). A 2
70
attack on the full misty1. In
IACR ePrint Archive, 2015/746. IACR.
Bar-On, A. (2015b). Improved higher-order dierential at-
tacks on misty1. In Fast Software Encryption 22nd
International Workshop. Springer.
CRYPTREC (2013). CRYPTREC ciphers list,
http://www.cryptrec.go.jp/english/method.html.
Dunkelman, O. and Keller, N. (2008). An improved im-
possible differential attack on misty1. In ASIACRYPT,
volume 5350 of LNCS, pages 441-454. Springer.
Dunkelman, O. and Keller, N. (2013). Practical-time attacks
against reduced variants of misty1. In IACR ePrint
Archive, 2013/431. IACR.
H. Tanaka, K. H. and Kaneko, T. (1999). Strength of misty1
without fl function for higher order differential attack.
In Applied Algebra, Algebraic Algorithms and Error-
Correcting Codes, volume 1719 of LNCS, pp 221-230.
Springer.
Igarashi, Y. and Kaneko, T. (2008). The 32nd-order differ-
ential attack on misty1 without fl functions. In 2008
International Symposium on Information Theory and
its Applications, No.W-TI-4-4, pages 1503-1508. IE-
ICE.
ISO (2010). ISO/IEC 18033-3 information technology -
security techniques - encryption algorithms - part 3:
Block ciphers.
Jia, K. and Li, L. (2012). Impossible differential at-
tacks on reduced-round misty1. In 13th International
Workshop, WISA, volume 7690 of LNCS pages 1527.
Springer.
Lai, X. (1994). Higher order derivatives and differential
cryptanalysis. In Communications and Cryptography,
pages 227-233.
Matsui, M. (1997). New block encryption algorithm misty.
In Fast Software Encryption 4th International Work-
shop. Springer.
T. Shimoyama, Siho Moriai, T. K. and Tsujii, S. (1999). Im-
proving higher order differential attack and its appli-
cation to nyberg-knudesen’s designed block cipher. In
IEIEC Transactions, Fundamentals, Vol.E82-A, No.9,
pages 1971-1980. IEICE.
Todo, Y. (2015). Integral cryptanalysis on full misty1. In
CRYPTO 2015 volume 9215 of LNCS, pages 413-432.
Springer.
Y. Hatano, H. T. and Kaneko, T. (2004). Optimization
for the algebraic method and its application to an at-
tack of misty1. In IEIEC Transactions, Fundamentals,
Vol.E87-A, No.1, pages 18-27. IEICE.
Y. Tsunoo, Teruo Saito, M. S. and Kawabata, T. (2008).
Higher order differential attacks on reduced-round
misty1. In ICISC, volume 5461 of LNCS, pages 415-
431. Springer.
Yi, W. and Chen, S. (2014). Multidimensional zero-
correlation linear attacks on reduced-round misty1. In
CoRR, abs/1410.4312.
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
242
