Capturing Graded Knowledge and Uncertainty in a Modalized

Fragment of OWL

Hans-Ulrich Krieger

German Reasearch Center for Artiﬁcial Intelligence (DFKI), Saarbr

ucken, Germany

Keywords:

Knowledge Representation and Reasoning, Uncertainty in AI, Description Logics & OWL, Ontologies,

Graded Natural Language Statements, Representation of Controlled Natural Language.

Abstract:

Natural language statements uttered in diagnosis (e.g., in medicine), but more general in daily life are usually

graded, i.e., are associated with a degree of uncertainty about the validity of an assessment and is often

expressed through speciﬁc verbs, adverbs, or adjectives in natural language. In this paper, we look into a

representation of such graded statements by presenting a simple non-standard modal logic which comes with

a set of modal operators, directly associated with the words indicating the uncertainty and interpreted through

conﬁdence intervals in the model theory. We complement the model theory by a set of RDFS-/OWL 2 RL-like

entailment (if-then) rules, acting on the syntactic representation of modalized statements. Our interest in such

a formalization is related to the use of OWL as the de facto language in today’s ontologies and its weakness to

represent and reason about assertional knowledge that is uncertain or that changes over time.

1 INTRODUCTION

Medical natural language statements uttered by physi-

cians or other health professionals and found in med-

ical examination letters are usually graded, i.e., are

associated with a degree of uncertainty about the va-

lidity of a medical assessment. This uncertainty is

often expressed through speciﬁc verbs, adverbs, ad-

jectives, or even phrases in natural language which

we will call gradation words (≈ linguistic hedges);

e.g., Dr. X suspects that Y suffers from Hepatitis or

The patient probably has Hepatitis or (The diagnosis

of) Hepatitis is conﬁrmed.

In this paper, we look into a representation of

such graded statements by presenting a simple non-

standard modal logic which comes with a small set

of partially-ordered modal operators, directly asso-

ciated with the words indicating the uncertainty and

interpreted through conﬁdence intervals in the model

theory. The work presented here addresses modal-

ized propositional formulae in negation normal form

which can be seen as a canonical representation of

natural language sentences of the above form (a kind

of a controlled natural language).

Our interest in such a formalization is related

to the use of OWL in our projects as the de facto

standard for (medical) ontologies today (to represent

structural/terminological knowledge) and its weak-

ness to represent and reason about assertional knowl-

edge that is uncertain (Schulz et al., 2014) or that

changes over time (Krieger, 2012). There are two

principled ways to address such a restriction: either

by sticking with the existing formalism (viz., OWL)

and trying to ﬁnd an encoding that still enables some

useful forms of reasoning (Schulz et al., 2014); or by

deviating from a deﬁned standard in order to arrive, at

best, at an easier, intuitive, and less error-prone repre-

sentation (Krieger, 2012).

Here, we follow the latter avenue, but employ

and extend the standard entailment rules from (Hayes,

2004; ter Horst, 2005; Motik et al., 2012) for pos-

itive binary relation instances in RDFS and OWL

towards modalized n-ary relation instances, includ-

ing negation. These entailment rules talk about,

e.g., subsumption, class membership, or transitiv-

ity, and have been found useful in many applica-

tions. The proposed solution has been implemented

for the binary relation case (extended triples, quads)

in HFC (Krieger, 2013), a forward chaining engine

that builds Herbrand models which are compatible

with the open-world view underlying OWL.

Our approach is clearly not restricted to medi-

cal statements, but is applicable to graded statements

in general, e.g., in technical diagnosis (the engine

is probably overheated) or in everyday conversation

(I’m pretty sure that Joe has signed a contract with

Krieger, H-U.

Capturing Graded Knowledge and Uncertainty in a Modalized Fragment of OWL.

DOI: 10.5220/0005628100190030

In Proceedings of the 8th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2016) - Volume 2, pages 19-30

ISBN: 978-989-758-172-4

 2016 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

Foo Inc.), involving trust (I’m not an expert, but ...)

which can be seen as the common case (contrary to

true universal statements).

2 OWL VS. MODALIZED

REPRESENTATION

We note here that the names of our initial modal op-

erators were inspired by the qualitative information

parts of diagnostic statements from (Schulz et al.,

2014) as shown in Figure 1.

Figure 1: Schematic mappings of the qualitative infor-

mation parts excluded (E), unlikely (U), not excluded (N),

likely (L), and conﬁrmed (C) to conﬁdence intervals. Picture

taken from (Schulz et al., 2014).

These qualitative parts were used in medical state-

ments about, e.g., liver inﬂammation with varying

levels of detail (Schulz et al., 2014) in order to infer,

e.g., if Hepatitis is conﬁrmed then Hepatitis is likely

but not Hepatitis is unlikely. And if Viral Hepatitis B

is conﬁrmed, then both Viral Hepatitis is conﬁrmed

and Hepatitis is conﬁrmed (generalization). Things

“turn around” when we look at the adjectival modi-

ﬁers excluded and unlikely: if Hepatitis is excluded

then Hepatitis is unlikely, but not Hepatitis is not ex-

cluded. Furthermore, if Hepatitis is excluded, then

both Viral Hepatitis is excluded and Viral Hepatitis B

is excluded (specialization).

(Schulz et al., 2014) consider ﬁve OWL encod-

ings, from which only two were able to fully repro-

duce the plausible inferences for the above Hepati-

tis use case. The encodings in (Schulz et al., 2014)

were quite cumbersome as the primary interest was to

stay within the limits of the underlying calculus. Be-

sides coming up with complex encodings, only minor

forms of reasoning were possible, viz., subsumption

reasoning. Furthermore, each combination of disease

and qualitative information part required a new OWL

class deﬁnition/new class name, and there exist a lot

of them!

These disadvantages are a result of two conscious

decisions: OWL only provides unary and binary re-

lations (concepts and roles) and comes up with a

(mostly) ﬁxed set of entailment/tableaux rules.

In our approach, however, the qualitative informa-

tion parts from Figure 1 are ﬁrst class citizens of the

object language (the modal operators) and diagnostic

statements from the Hepatitis use case are expressed

through the binary property suffersForm between p

(patients, people) and d (diseases, diagnoses). The

plausible inferences are then simply a byproduct of

the instantiation of the entailment rule schemas (G)

from Section 5.1, and (S1) and (S0) from Section 5.2

for property suffersForm (the rule variables are uni-

versally quantiﬁed; > = universal truth; C = con-

ﬁrmed; L = likely), e.g.,

(S1) ViralHepatitisB v ViralHepatitis ∧

>ViralHepatitisB(d) → >ViralHepatitis(d)

(G) CsuffersFrom(p, d) → LsuffersFrom(p,d)

Two things are worth mentioning here. Firstly,

not only OWL properties can be graded, such as

CsuffersFrom(p, d) (= it is conﬁrmed that p suf-

fers from d), but also class membership, e.g.,

CViralHepatitisB(d) (= it is conﬁrmed that d is of

type Viral Hepatitis B). As the original OWL exam-

ple from (Schulz et al., 2014) can not make use of

any modals, we employ the special modal > here:

>ViralHepatitisB(d). Secondly, modal operators are

only applied to assertional knowledge (the ABox in

OWL)—neither TBox nor RBox axioms are being af-

fected by modals in our approach, as they are sup-

posed to express universal truth.

3 CONFIDENCE AND

CONFIDENCE INTERVALS

We address the conﬁdence of an asserted (medical)

statement (Schulz et al., 2014) through graded modal-

ities applied to propositional formulae: E (excluded),

U (unlikely), N (not excluded), L (likely), and C (con-

ﬁrmed). For various (technical) reasons, we add a

wildcard modality ? (unknown), a complementary

failure modality ! (error), plus two further modali-

ties to syntactically state deﬁnite truth and falsity: >

(true) and ⊥ (false).

Let 4 now denotes the set of all modalities:

4 := {?,!,>,⊥, E,U,N,L,C}

A measure function

µ : 4 7→ [0,1] × [0, 1]

We also call > and ⊥ propositional modals as they lift

propositional statements to the modal domain. We refer to ?

and ! as completion modals since they complete the modal

hierarchy by adding unique most general and most speciﬁc

elements (see Section 4.3).

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

is a mapping which returns the associated conﬁdence

interval µ(δ) = [l,h] for a modality from δ ∈ 4 (l ≤

h). We presuppose that

• µ(?) = [0,1]

• µ(>) = [1,1]

• µ(⊥) = [0,0]

• µ(!) =

In addition, we deﬁne two disjoint subsets of 4,

called

1 := {>,C,L, N}

and

0 := {⊥,E,U }

and again make a presupposition: the conﬁdence in-

tervals for modals from 1 end in 1, whereas the conﬁ-

dence intervals for 0 modals always start with 0. It is

worth noting that we do not make use of µ in the syn-

tax of the modal language (for which we employ the

modalities from 4), but in the semantics when deal-

ing with the satisfaction relation of the model theory

(see Section 4).

We have talked about conﬁdence intervals now

several times without saying what we actually mean

by this. Suppose that a physician says that it is con-

ﬁrmed (= C) that patient p suffers from disease d,

for a set of observed symptoms (or evidence) S =

,. ..,S

}: CsuffersFrom(p,d).

Assuming that a different patient p

shows the

same symptoms S (and only S, and perhaps further

symptoms which are, however, independent from S),

we would assume that the same doctor would diag-

nose CsuffersFrom(p

,d).

Even an other, but similar trained physician is

supposed to grade the two patients similarly. This

similarity which originates from patients showing the

same symptoms and from physicians being taught at

the same medical school is addressed by conﬁdence

intervals and not through a single (posterior) prob-

ability, as there are still variations in diagnostic ca-

pacity and daily mental state of the physician. By us-

ing intervals (instead of single values), we can usually

reach a consensus among people upon the meaning of

gradation words, even though the low/high values of

the conﬁdence interval for, e.g., conﬁrmed might de-

pend on the context.

Being a bit more theoretic, we deﬁne a conﬁdence

interval as follows. Assume a Bernoulli experiment

(Krengel, 2003) that involves a large set of n patients

Recall that intervals are (usually inﬁnite) sets of real

numbers, together with an ordering relations (e.g., < or ≤)

over the elements, thus

0 is a perfect, although degraded

interval.

P, sharing the same symptoms S. W.r.t. our exam-

ple, we would like to know whether suffersFrom(p,d)

or ¬suffersFrom(p,d) is the case for every patient

p ∈ P, sharing S. Given a Bernoulli trials sequence

X = (X

,. ..,X

) with indicator random variables X

∈

{0,1} for a patient sequence (p

,. .., p

), we can ap-

proximate the expected value E for suffersFrom being

true, given disease d and background symptoms S by

the arithmetic mean A:

X] ≈ A[

X] =

∑

i=1

Due to the law of large numbers, we expect that

if the number of elements in a trials sequence goes

to inﬁnity, the arithmetic mean will coincide with the

expected value:

X] = lim

n→∞

∑

i=1

Clearly, the arithmetic mean for each new ﬁnite

trials sequence is different, but we can try to locate

the expected value within an interval around the arith-

metic mean:

X] ∈ [A[

X] − ε

,A[

X] + ε

]

For the moment, we assume ε

= ε

, so that A[

is in the center of this interval which we will call from

now on conﬁdence interval.

Coming back to our example and assuming

µ(C) = [0.9,1], CsuffersFrom(p,d) can be read as

being true in 95% of all cases known to the physi-

cian, involving patients p potentially having disease

d and sharing the same prior symptoms (evidence)

,. ..,S

∑

p∈P

Prob(suffersFrom(p,d)|S)

≈ 0.95

The variance of ±5% is related to varying diag-

nostic capabilities between (comparative) physicians,

daily mental form, undiscovered important symptoms

or examinations which have not been carried out (e.g.,

lab values), or perhaps even by the physical stature of

the patient (crooked vs. upright) which unconsciously

affects the ﬁnal diagnosis, etc, as elaborated above.

Thus the individual modals from 4 express (via µ)

different forms of the physician’s conﬁdence, depend-

ing on the set of already acquired symptoms as (po-

tential) explanations for a speciﬁc disease.

4 MODEL THEORY AND

NEGATION NORMAL FORM

Let C denote the set of constants that serve as the

arguments of a relation instance. For instance, in

Capturing Graded Knowledge and Uncertainty in a Modalized Fragment of OWL

an RDF/OWL setting, C would exclusively consist

of XSD atoms, blank nodes, and URIs/IRIs. In

order to deﬁne basic n-ary propositional formulae

(ground atoms), let p(~c) abbreviates p(c

,. ..,c

), for

,. ..,c

∈ C, given length(~c) = n. In case the num-

ber of arguments does not matter, we sometimes sim-

ply write p, instead of, e.g., p(c,d) or p(~c). As before,

we assume 4 = {?,!,>,⊥,E,U,N,L,C}. We induc-

tively deﬁne the set of well-formed formulae φ of our

modal language as follows:

φ ::= p(~c) | ¬φ | φ ∧ φ

| φ ∨ φ

| 4φ

4.1 Simpliﬁcation and Normal Form

We now syntactically simplify the set of well-formed

formulae φ by restricting the uses of negation and

modalities to the level of propositional letters π:

π ::= p(~c) | ¬p(~c)

φ ::= π | 4π | φ ∧ φ

| φ ∨ φ

The design of this language is driven by two main

reasons: ﬁrstly, we want to effectively implement the

logic (in our case, in HFC), and secondly, the applica-

tion of the below semantic-preserving simpliﬁcation

rules in an ofﬂine pre-processing step makes the im-

plementation easier and guarantees a more efﬁcient

runtime system. To address negation, we ﬁrst need

the notion of a complement modal δ

for every δ ∈ 4,

where

µ(δ

) := µ(δ)

= µ(?) \ µ(δ) = [0, 1] \ µ(δ)

I.e., µ(δ

) is deﬁned as the complementary inter-

val of µ(δ) (within the bounds of [0,1], of course). For

example, E and N (excluded, not excluded) or ? and !

(unknown, error) are already existing complementary

modals.

We also require mirror modals δ

for every δ ∈ 4

whose conﬁdence interval µ(δ

) is derived by “mir-

roring” µ(δ) to the opposite side of the conﬁdence in-

terval, either to the left or to the right:

if µ(δ) = [l, 1] then µ(δ

) := [0, 1 − l]

if µ(δ) = [0,h] then µ(δ

) := [1 − h,1]

It is easy to see that these two equations can be

uniﬁed and generalized

if µ(δ) = [l, h] then µ(δ

) := [1 − h,1 − l]

For example, E and C (excluded, conﬁrmed) or >

and ⊥ (top, bottom) are mirror modals. In order to

This construction procedure comes in handy when

dealing with in-the-middle modals, such as ﬁfty-ﬁfty or per-

haps, whose conﬁdence intervals neither touch 0 nor 1.

Such modals have a real background in (medical) diagnosis.

transform φ into its negation normal form, we need

to apply simpliﬁcation rules a ﬁnite number of times

(until rules are no longer applicable). We depict those

rules by using the ` relation, read as formula ` sim-

pliﬁed formula (ε = empty word):

1. ?φ ` ε % ?φ is not informative at all

2. ¬¬φ ` φ

3. ¬(φ ∧ φ

) ` ¬φ ∨ ¬φ

4. ¬(φ ∨ φ

) ` ¬φ ∧ ¬φ

5. ¬4φ ` 4

φ (example: ¬Eφ = E

φ = Nφ)

6. 4¬φ ` 4

φ (example: E¬φ = E

φ = Cφ)

Clearly, the mirror modals δ

(δ ∈ 4) are not nec-

essary as long as we explicitly allow for negated state-

ments (which we do), and thus case 6 can, in princi-

ple, be dropped.

What is the result of simplifying 4(φ ∧ φ

) and

4(φ ∨ φ

)? Let us start with the former case and con-

sider as an example the statement about an engine that

a mechanical failure m and an electrical failure e is

conﬁrmed: C(m ∧ e). It seems plausible to simplify

this expression to Cm ∧ Ce. Commonsense tells us

furthermore that neither Em nor Ee is compatible with

this description (we should be alarmed if, e.g., both

Cm and Em happen to be the case).

Now consider the “opposite” statement E(m ∧ e)

which must not be rewritten to Em∧ Ee, as either Cm

or Ce is well compatible with E(m ∧ e). Instead, we

rewrite this kind of “negated” statement as Em ∨ Ee,

and this works ﬁne with either Cm or Ce.

In order to address the other modal operators, we

generalize these plausible inferences by making a dis-

tinction between 0 and 1 modals (cf. Section 3):

7a. 0(φ ∧ φ

) ` 0φ ∨ 0φ

7b. 1(φ ∧ φ

) ` 1φ ∧ 1φ

Let us now focus on disjunction inside the scope

of a modal operator. As we do allow for the full set of

Boolean operators, we are allowed to deduce

8. 4(φ∨φ

) ` 4(¬(¬(φ∨φ

))) ` 4(¬(¬φ∧¬φ

)) `

(¬φ ∧ ¬φ

)

This is, again, a conjunction, so we apply schemas

7a and 7b, giving us

8a. 0

(φ ∨ φ

) ` 0

(¬φ ∧ ¬φ

) ` 1(¬φ ∧ ¬φ

) ` 1¬φ ∧

1¬φ

` 1

φ ∧ 1

` 0φ ∧ 0φ

8b. 1(φ ∨ φ

) ` 1

(¬φ ∧ ¬φ

) ` 0(¬φ ∧ ¬φ

) ` 0¬φ ∨

0¬φ

` 0

φ ∨ 0

` 1φ ∨ 1φ

Note how the modals from 0 in 7a and 8a act as a

kind of negation operator to turn the logical operators

into their counterparts, similar to de Morgan’s law.

The ﬁnal case considers two consecutive modals:

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

9. δ

φ ` (δ

◦ δ

)φ

We interpret the ◦ operator as a kind of function

composition, leading to a new modal δ which is the

result of δ

◦ δ

. We take a liberal stance here of what

the result is, but indicate that it depends on the do-

main and, again, plausible inferences we like to cap-

ture. The ◦ operator will probably be different from

the related operation  which is used in Section 5.3.4.

4.2 Model Theory

In the following, we extend the standard deﬁnition of

modal (Kripke) frames and models (Blackburn et al.,

2001) for the graded modal operators from 4 by em-

ploying the conﬁdence function µ and focussing on

the minimal deﬁnition for φ. A frame F for the prob-

abilistic modal language is a pair

F = hW ,4i

where W is a non-empty set of worlds (or situations,

states, points, vertices, etc.) and 4 a family of binary

relations over W × W , called accessibility relations.

In the following, we overload δ ∈ 4 below in that we

let δ both refer to the modal in the syntax as well as

to the accessibility relation R

in the semantics.

A model M for the probabilistic modal language

is a triple

M = hF , V ,µi

such that F is a frame, V is a valuation, assigning

each proposition φ a subset of W , viz., the set of

worlds in which φ holds, and µ is a mapping, returning

the conﬁdence interval for a given modality from 4.

Note that we only require a deﬁnition for µ in M (the

model, but not in the frame), as F represents the rela-

tional structure without interpreting the edge labeling

(the modal names) of the graph.

The satisfaction relation |=, given a model M and

a speciﬁc world w is inductively deﬁned over the set

of well-formed formulae in negation normal form (re-

member π ::= p(~c) | ¬p(~c)):

1. M ,w |= p(~c) iff w ∈ V (p(~c)) and w 6∈ V (¬p(~c))

2. M ,w |= ¬p(~c) iff w ∈ V (¬p(~c)) and

w 6∈ V (p(~c))

3. M ,w |= φ ∧ φ

iff M , w |= φ and M ,w |= φ

4. M ,w |= φ ∨ φ

iff M , w |= φ or M ,w |= φ

5. for all δ ∈ 4: M ,w |= δπ iff

#{u | (w, u) ∈ δ and M , u |= π}

# ∪

∈4

{u | (w,u) ∈ δ

}

∈ µ(δ)

The last case of the satisfaction relation addresses

the modals: for a world w, we look for the successor

states u that are directly reachable via δ and in which

π holds, and divide the number of such states (#·) by

the number of all worlds that are reachable from w in

the denominator. This number, lying between 0 and

1, is then required to be an element of the conﬁdence

interval µ(δ) of δ in order to satisfy δπ, given M ,w.

It is worth noting that the satisfaction relation

above differs from the standard deﬁnition in its han-

dling of M ,w |= ¬p(~c), as negation is not inter-

preted through the absence of p(~c) (M ,w 6|= p(~c)),

but through the existence of ¬p(~c). This treatment

addresses the open-world nature in OWL and the

evolvement of a (medical) domain over time.

We also note that the deﬁnition of the satisfaction

relation for modalities (last clause) is related to the

possibility operators M

· (= ♦

≥k

·; k ∈ N) introduced

by (Fine, 1972) and counting modalities · ≥ n (Areces

et al., 2010), used in modal logic characterizations of

description logics with cardinality restrictions.

4.3 Well-behaved Frames

As we will see later, it is handy to assume that the

graded modals are arranged in a kind of hierarchy—

the more we move along the arrows in the hierar-

chy, the more a statement φ in the scope of a modal

δ ∈ 4 becomes uncertain. In order to address this, we

slightly extend the notion of a frame by a third com-

ponent  ⊆ 4 × 4, a partial order (i.e., a reﬂexive,

antisymmetric, and transitive binary relation) between

modalities:

F = hW ,4, i

Let us consider the following modal hierarchy that

we build from the set 4 of already introduced modals

(cf. Figure 1):

⊥

This graphical representation is just a compact

way to specify a set of 33 binary relation instances

over 4 × 4, such as >  >, >  N, C  N, ⊥  ?,

or !  ?. The above mentioned form of uncertainty is

expressed by the measure function µ in that the asso-

ciated conﬁdence intervals become larger:

if δ  δ

then µ(δ) ⊆ µ(δ

)

In order to arrive at a proper and intuitive model-

theoretic semantics which mirrors intuitions such as

if φ is conﬁrmed (Cφ) then φ is likely (Lφ), we will

Capturing Graded Knowledge and Uncertainty in a Modalized Fragment of OWL

focus here on well-behaved frames F which enforce

the existence of edges in W , given  and δ,δ

↑

∈ 4:

if (w, u) ∈ δ and δ  δ

↑

then (w, u) ∈ δ

↑

However, by imposing this constraint, we also

need to adapt the last case of the satisﬁability relation

from Section 4.2 above:

5. for all δ ∈ 4: M ,w |= δπ iff

# ∪

↑

δ

{u | (w,u) ∈ δ

↑

and M , u |= π}

# ∪

∈4

{u | (w,u) ∈ δ

}

∈ µ(δ)

Not only are we scanning for edges (w,u) labeled

with δ and for successor states u of w in which π holds

in the numerator (original deﬁnition), but also take

into account edges marked with more general modals

↑

: δ

↑

 δ. This mechanism implements a kind of

built-in model completion that is not necessary in or-

dinary modal logics as they deal with only a single

relation (viz., unlabeled arcs).

5 ENTAILMENT RULES

We now turn our attention, again, to the syntax of our

language and to the syntactic consequence relation.

This section addresses a restricted subset of entail-

ment rules which will unveil new (or implicit) knowl-

edge from already existing graded statements. Re-

call that these kind of statements (in negation normal

form) are a consequence of the application of simpli-

ﬁcation rules as depicted in Section 4.1. Thus, we

assume a pre-processing step here that “massages”

more complex statements that arise from a represen-

tation of graded (medical) statements in natural lan-

guage. The entailments which we will present in a

moment can either be directly implemented in a tuple-

based reasoner, such as HFC (Krieger, 2013), or in

triple-based engines (e.g., Jena (Carroll et al., 2004)

or OWLIM (Bishop et al., 2011)) which need to reify

the medical statements in order to be compliant with

the RDF triple model.

5.1 Modal Entailments

The entailments presented in this section deal with

plausible inference centered around modals δ, δ

∈ 4

which are, in part, also addressed in (Schulz et al.,

2014) in a pure OWL setting. We use the implication

sign → to depict the entailment rules

lhs → rhs

which act as completion (or materialization) rules

the way as described in, e.g., (Hayes, 2004) and (ter

Horst, 2005), and used in today’s semantic reposito-

ries (e.g., OWLIM ). We sometimes even use the bi-

conditional ↔ to address that the LHS and the RHS

are semantically equivalent, but will indicate the di-

rection that should be used in a practical setting. As

before, we deﬁne

π ::= p(~c) | ¬p(~c)

We furthermore assume that for every modal δ ∈

4, a complement modal δ

and a mirror modal δ

exist (cf. Section 4.1).

5.1.1 Lift

(L) π ↔ >π

This rule interprets propositional statements as spe-

cial modal formulae. It might be dropped and can be

seen as a pre-processing step. We have used it in the

Hepatitis example above. Usage: left-to-right direc-

tion.

5.1.2 Generalize

(G) δπ∧ δ  δ

→ δ

This rule schema can be instantiated in various ways,

using the modal hierarchy from Section 4.3, e.g.,

>π → Cπ, Cπ → Lπ, or Eπ → U π. It has been used

in the Hepatitis example.

5.1.3 Complement

In principle, (C) is not needed in case the statement is

already in negation normal form. This schema might

be useful for natural language paraphrasing (explana-

tion). Given 4, there are four possible instantiations:

Eπ ↔ ¬Nπ, Nπ ↔ ¬Eπ, ?π ↔ ¬!π, and !π ↔ ¬?π.

5.1.4 Mirror

(M) δ¬π ↔ δ

Again, (D) is in principle not needed as long as

the modal proposition is in negation normal form,

since we do allow for negated propositional state-

ments ¬p(~c). This schema might be useful for nat-

ural language paraphrasing (explanation). For 4,

there are six possible instantiations, viz., Eπ ↔ C¬π,

Cπ ↔ E¬π, Lπ ↔ U¬π, Uπ ↔ L¬π, >π ↔ ⊥¬π, and

⊥π ↔ >¬π.

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

5.1.5 Uncertainty

(U) δπ∧ ¬δπ ↔ δπ ∧ δ

π ↔ ?π

The co-occurrence of δπ and ¬δπ does not imply log-

ical inconsistency (propositional case: π ∧ ¬π), but

leads to complete uncertainty about the validity of π.

Remember that µ(?) = µ(δ) ] µ(δ

) = [0, 1]:

0 1

µ : |—δ

—|——δ——|

π π

Usage: left-to-right direction.

5.1.6 Negation

(N) δ(π∧ ¬π) ↔ δπ ∧ δ¬π ↔ δπ ∧ δ

π ↔

¬π ∧ δ

π ↔ δ

(π ∧ ¬π)

(N) shows that δ(π ∧ ¬π) can be formulated equiva-

lently by using the mirror modal δ

0 1

µ : |—δ

—|——|—δ —|

π ∧ ¬π π ∧ ¬π

In general, (N) is not the modal counterpart of the law

of non-contradiction, as π ∧ ¬π is usually afﬂicted by

uncertainty, meaning that from δ(π ∧ ¬π), we can not

infer that π ∧ ¬π is the case for the concrete example

in question (recall the intention behind the conﬁdence

intervals; cf. Section 3). There is one notable excep-

tion, involving the > and ⊥ modals. This is formu-

lated by the next entailment rule.

5.1.7 Error

(E) >(π∧¬π) ↔ ⊥(π ∧ ¬π) → !(π ∧ ¬π) ↔ !π

(E) is the modal counterpart of the law of non-

contradiction (note: ⊥

= >, >

= ⊥, !

= !). For

this reason and by deﬁnition, the error (or failure)

modal ! from Section 3 comes into play here. The

modal ! can serve as a hint to either stop a compu-

tation the ﬁrst time it occurs, or to continue reason-

ing and to syntactically memorize the ground literal

π. Usage: left-to-right direction.

5.2 Subsumption Entailments

As before, we deﬁne two subsets of 4, called 1 =

{>,C,L,N} and 0 = {⊥,E,U }, thus 1 and 0 effec-

tively become

1 = {>,C,L,N,U

} 0 = {⊥,U, E,C

}

due to the use of complement modals δ

and mirror

modals δ

for every base modal δ ∈ 4 and by as-

suming that E = N

, E = C

, U = L

, and ⊥ = >

together with the four “opposite” cases.

Now, let v abbreviate relation subsumption as

known from description logics and realized through

rdfs:subClassOf and rdfs:subPropertyOf.

Given this, we deﬁne two further very practical and

plausible modal entailments which can be seen as the

modal extension of the entailment rules (rdfs9) and

(rdfs7) for classes and properties in RDFS (Hayes,

2004):

(S1) 1p(~c) ∧ p v q → 1q(~c)

(S0) 0q(~c) ∧ p v q → 0p(~c)

Note how the use of p and q switches in the an-

tecedent and the consequent, even though p v q holds

in both cases. Note further that propositional state-

ments π are restricted to the positive case p(~c) and

q(~c), as their negation in the antecedent will not lead

to any valid entailments.

Here are four instantiations of (S0) and (S1) for

the unary and binary case (remember, C ∈ 1 and E ∈

0):

ViralHepatitisB v ViralHepatitis ∧

CViralHepatitisB(x) → CViralHepatitis(x)

ViralHepatitis v Hepatitis ∧

EHepatitis(x) → EViralHepatitis(x)

deeplyEnclosedIn v containedIn ∧

CdeeplyEnclosedIn(x, y) → CcontainedIn(x, y)

superﬁciallyLocatedIn v containedIn ∧

EcontainedIn(x,y)→EsuperﬁciallyLocatedIn(x,y)

5.3 Extended RDFS & OWL

Entailments

In this section, we will consider further entailment

rules for RDFS (Hayes, 2004) and a restricted subset

of OWL (ter Horst, 2005; Motik et al., 2012). Re-

member that modals only head positive and negative

propositional letters π, not TBox or RBox axioms.

Concerning the original entailment rules, we will dis-

tinguish four principal cases to which the extended

rules belong (we will only consider the unary and bi-

nary case here as used in description logics/OWL):

1. TBox and RBox axiom schemas will not undergo

a modal extension;

2. rules get extended in the antecedent;

3. rules take over modals from the antecedent to the

consequent;

4. rules aggregate several modals from the an-

tecedent in the consequent.

We will illustrate the individual cases in the fol-

lowing subsections with examples by using a kind of

description logic rule syntax. Clearly, the set of ex-

tended entailments depicted here is not complete.

Capturing Graded Knowledge and Uncertainty in a Modalized Fragment of OWL

5.3.1 Case-1: No Modals

Entailment rule (rdfs11) from (Hayes, 2004) deals

with class subsumption: C v D ∧ D v E → C v E.

As this is a terminological axiom schema, the rule

stays constant in the modal domain. Example rule

instantiation:

ViralHepatitisB v ViralHepatitis ∧

ViralHepatitis v Hepatitis →

ViralHepatitisB v Hepatitis

5.3.2 Case-2: Modals on LHS, No Modals on

RHS

The following original rule (rdfs3) from (Hayes,

2004) imposes a range restriction on objects of binary

ABox relation instances: ∀P.C ∧ P(x,y) → C(y). The

extended version needs to address the ABox proposi-

tion in the antecedent (don’t care modal δ), but must

not change the consequent (even though we always

use the > modality here—the range restriction C(y) is

always true, independent of the uncertainty of P(x, y);

cf. Section 2 example):

(Mrdfs3) ∀P.C ∧δP(x,y) → >C(y)

Example rule instantiation:

∀suffersFrom.Disease ∧ LsuffersFrom(x,y) →

>Disease(y)

5.3.3 Case-3: Keeping LHS Modals on RHS

Inverse properties switch their arguments

(ter Horst, 2005) as described by (rdfp8):

P ≡ Q

−

∧ P(x,y) → Q(y,x). The extended ver-

sion simply keeps the modal operator:

(Mrdfp8) P ≡ Q

−

∧ δP(x,y) → δQ(y,x)

Example rule instantiation:

containedIn ≡ contains

−

∧ CcontainedIn(x, y) →

Ccontains(y,x)

5.3.4 Case-4: Aggregating LHS Modals on RHS

Now comes the most interesting case of modalized

RDFS & OWL entailment rules, that offers several

possibilities on a varying scale between skeptical and

credulous entailments, depending on the degree of un-

certainty, as expressed by the measuring function µ of

the modal operator. Consider the original rule (rdfp4)

from (ter Horst, 2005) for transitive properties:

v P ∧ P(x,y) ∧ P(y,z) → P(x,z).

Now, how does the modal on the RHS of the ex-

tended rule look like, depending on the two LHS

modals? There are several possibilities. By operat-

ing directly on the modal hierarchy, we are allowed to

talk about, e.g., the least upper bound or the greatest

lower bound of δ

and δ

. When taking the associ-

ated conﬁdence intervals into account, we might play

with the low and high numbers of the intervals, say,

by applying min/max, the arithmetic mean or even by

multiplying the corresponding numbers.

Let us ﬁrst consider the general rule from which

more specialized versions can be derived, simply by

instantiating the combination operator :

(Mrdfp4) P

v P ∧ δ

P(x,y) ∧ δ

P(y,z) →

(δ

 δ

)P(x,z)

Here is an instantiation of Mrdfp4, dealing with the

transitive relation contains from above, assuming that

 reduces to the least upper bound (i.e., C  L = L):

Ccontains(x, y) ∧ Lcontains(y,z) →

Lcontains(x,z)

What is the general result of δ

 δ

? It depends,

probably both on the application domain and the epis-

temic commitment one is willing to accept about the

“meaning” of gradation words/modal operators. To

enforce that  is at least both commutative and as-

sociative (as is the least upper bound) is probably a

good idea, making the sequence of modal clauses or-

der independent. And to work on the modal hierarchy

instead of combining low/high numbers of the cor-

responding intervals is probably a good decision for

forward chaining engines, as the latter strategy might

introduce new individuals through operations such as

multiplication, thus posing a problem for the imple-

mentation of the generalization schema (G) (see Sec-

tion 5.1.2).

5.4 Custom Entailments: An Example

from the Medical Domain

Consider that Hepatitis B is an infectious disease

ViralHepatitisB v InfectiousDisease v Disease

and note that there exist vaccines against it. Assume

that the liver l of patient p quite hurts

ChasPain(p, l),

but p has been deﬁnitely vaccinated against Hepatitis

B before:

>vaccinatedAgainst(p, ViralHepatitisB).

We apply OWL2-like punning here when using the

class ViralHepatitisB (not an instance), as the second

argument of vaccinatedAgainst; cf. (Golbreich and

Wallace, 2012).

Given that p received a vaccination, the follow-

ing custom rule will not ﬁre (x, y below are now

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

universally-quantiﬁed variables; z an existentially-

quantiﬁed RHS-only variable):

>Patient(x) ∧ >Liver(y) ∧ ChasPain(x,y) ∧

UvaccinatedAgainst(x,ViralHepatitisB) →

NViralHepatitisB(z) ∧ NsuffersFrom(x,z)

Now assume another person p

that is pretty sure (s)he

was never vaccinated:

EvaccinatedAgainst(p

,ViralHepatitisB)

Given the above custom rule, we are allowed to infer

that (h instantiation of z)

NViralHepatitisB(h) ∧ NsuffersFrom(p

,h)

The subclass axiom from above thus assigns

NInfectiousDisease(h)

so that we can query for patients for whom an infec-

tious disease is not excluded (= N), in order to initiate

appropriate methods (e.g., further medical investiga-

tions).

5.5 Implementing Modal Entailments

The negation normal form from Section 4.1 makes

it relatively easy to implement entailment rules in-

volving modalized propositional letters of the form

δ ± p(~c). ± is a polarity value as known from situ-

ation theory (Devlin, 2006) in order to make negative

property assertions available in the object language.

We have implemented a modalized extension of

the RDFS and OWL rule sets (Hayes, 2004; ter Horst,

2005) by employing the tuple-based rule engine HFC

(Krieger, 2012; Krieger, 2013). Without loss of gen-

erality, let us focus here on the positive case for the

three binary entailment schemas from Section 5.3.2,

5.3.3, and 5.3.4 and their HFC rule representation, as

negation inside the scope of a modal can be rewrit-

ten using the mirror modal, thus turning the quintuple

into a quad (rule variables start with a ?):

(Mrdfs3) ∀P.C ∧δP(x,y) → >C(y)

?p rdfs:range ?c

?modal ?x ?p ?y

mod:T ?y rdf:type ?c

(Mrdfp8) P ≡ Q

−

∧ δP(x,y) → δQ(y,x)

?p owl:inverseOf ?q

?modal ?x ?p ?y

?modal ?y ?q ?x

(Mrdfp4) P

v P ∧ δP(x,y) ∧ δ

P(y,z) →

(δ  δ

)P(x,z)

?p rdf:type owl:TransitiveProperty

?modal1 ?x ?p ?y

?modal2 ?y ?p ?z

?modal ?x ?p ?z

@action

?modal = CombineModals ?modal1 ?modal2

Triple-based engines, such as OWLIM clearly

need to reify such extended descriptions (expensive;

no termination guarantee). Even more important, ad-

ditional tests going beyond simple symbol match-

ing and function calls, such as CombineModals (the

equivalent to  in the abstract syntax) in the HFC

version of (Mrdfp4) above, are rarely available in to-

day’s RDFS/OWL reasoning engines, thus making it

impossible for them to implement such modal entail-

ments.

We ﬁnally describe how the implementation of the

generalization schema (G) (Section 5.1.2) works. As

explained in Section 4.3, the modal operators δ are

arranged in a modal hierarchy that is based on the in-

clusion of their conﬁdence intervals µ(δ). This hierar-

chy is realized in OWL through a subclass hierarchy,

using rdfs:subClassOf to implement :

(G) δP(x,y) ∧ δ  δ

→ δ

P(x,y)

?modal1 ?x ?p ?y

?modal1 rdfs:subClassOf ?modal2

?modal2 ?x ?p ?z

6 A FOURTH KIND OF MODALS

The two modalities  and ♦ from standard modal

logic are often called dual as they can be deﬁned in

terms of each other: φ ≡ ¬♦¬φ and ♦φ ≡ ¬¬φ,

resp. At ﬁrst sight, it seems that our non-standard

modal logic is missing a similar property, as we origi-

nally dealt with ﬁve modal operators, extended by the

propositional modals > and ⊥, and the completion

modals ? and !. For every such modal δ, we can fur-

thermore think of additional complement modals δ

and additional mirror modals δ

whose conﬁdence

intervals µ(δ

) and µ(δ

) can be derived from µ(δ)

(cf. Section 4.1). Some of these modals coincide with

original modals from 4, others do not have a direct

counterpart. However, the conﬁdence intervals for

the “anonymous” modals can be trivially computed

by applying the two equations from Section 4.1.

Coming back to the question of whether dual

modals exist for every δ ∈ 4, we need to simplify

¬δ¬φ by applying the schemas from Section 4.1. We

can either start with the inner or with the outer nega-

tion, resulting in either mirror modals or complement

Capturing Graded Knowledge and Uncertainty in a Modalized Fragment of OWL

modals. Interestingly, the resulting conﬁdence inter-

vals at which we reach in the end are the same, and

this is clearly a good point and desirable, as simpli-

ﬁcation is supposed to be an order-independent pro-

cess:

¬δ¬φ

/ \

¬φ ¬δ

| |

φ δ

Thus, δ

≡ δ

, for every δ ∈ 4 which can be

shown by applying the deﬁnitions for complement

and mirror modals from Section 4.1. The deeper rea-

son why this is so is related to the inherent properties

of the two operations complementation and mirror-

ing. Contrary to complement and mirror modals, dual

modals δ

are either supersets or subsets of µ(δ), i.e.,

if δ is a 1- or 0-modal, so is δ

7 RELATED WORK & REMARKS

It is worth noting to state that this paper is interested

in the representation of and reasoning with uncertain

assertional knowledge, and neither in dealing with

vagueness/fuzziness found in natural language (very

small, hot), nor in handling defaults and exceptions in

terminological knowledge (penguins can’t ﬂy).

To the best of our knowledge, the modal logic pre-

sented in this paper uses for the ﬁrst time modal op-

erators for expressing the degree of (un)certainty of

propositions. These modal operators are interpreted

in the model theory through conﬁdence intervals via

measure function µ. From a model point of view,

our modal operators are related to counting modali-

ties ♦

≥k

(Fine, 1972; Areces et al., 2010). However,

for M ,w |= δπ to be the case, we do not require a ﬁxed

number k ∈ N of reachable successor states (absolute

frequency), but instead divide the number of worlds

reached through label δ ∈ 4 and in which π holds by

the number of all directly reachable worlds, yielding

fraction 0 ≤ p ≤ 1. This number then is further con-

strained by requiring p ∈ µ(δ) (relative frequency), as

deﬁned in case 5 of the satisfaction relation in Section

4.2 and extended in Section 4.3.

As (Wikipedia, 2015) precisely put it: “... what

axioms and rules must be added to the propositional

calculus to create a usable system of modal logic is

a matter of philosophical opinion, often driven by

the theorems one wishes to prove ...”. Clearly, the

logic presented here is no exception and its design is

driven by commonsense knowledge and plausible in-

ferences, we try to capture and generalize. In a strict

sense, it is a non-standard modal logic in that it is not

an instance of the normal modal logic K = (N) + (K)

(N) p → p

(K) (p → q) → (p → q)

as the necessitation rule (N) and the distribution ax-

iom (K) does not hold for every δ ∈ 4. However, we

can show that restricted generalized forms of these

axioms are in fact the case for our logic (1

≥0.5

are

1-modals whose low value is ≥ 0.5 and 0

≤0.5

are 0-

modals whose high value is ≤ 0.5):

(N1) p → 1p

(N0) ¬p → 0p

(K1

≥0.5

) 1

≥0.5

(p → q) → (1

≥0.5

p → 1

≥0.5

(K0

≤0.5

) 0

≤0.5

(p → q) → (0

≤0.5

p → 0

≤0.5

In addition, the well-behaved frames condition

(Section 4.3) generalizes the seriality condition (D)

on frames and a kind of forward monotonicity, we

would like to keep for an evolving domain, is directly

related to transitivity (4) of the accessibility relations

from 4 in F :

(D) δp ∧ δ  δ

→ δ

(4) δp → δδp

Several approaches to representing and reason-

ing with uncertainty have been investigated in Ar-

tiﬁcial Intelligence; see (Halpern, 2003) for a (bi-

ased) overview. (Halpern, 1990) was probably the

ﬁrst attempt of a ﬁrst-order logic which uniﬁes prob-

ability distributions over classes and individuals.

Weaker decidable propositional formalisms such as

Bayesian Networks (Pearl, 1988) and related prob-

abilistic graphical models (Koller and Friedmann,

2009) have found their way into causal (medical)

reasoning (Lucas et al., 2004). Programming lan-

guages for these kind of models exist; e.g., Alchemy

for Markov Logic Networks (Richardson and Domin-

gos, 2006). In Markov Logic, ﬁrst-order formulae

are associated with a numerical value which softens

hard ﬁrst-order constraints and a violation makes a

possible world not impossible, but less probable (the

higher the weight, the stronger the rule). For example,

the Markov Logic rule smoking causes cancer with

weight 1.5 (Richardson and Domingos, 2006, p. 111)

1.5 : ∀x. smokes(x) → hasCancer(x)

might be approximated in our approach through the

use of modals:

>smokes(x) → LhasCancer(x)

Very less so has been researched in the Descrip-

tion Logic community (as it is smaller) and little or

nothing of this research has ﬁnd its way into imple-

mented description logic systems. As we focus in

this paper on a modalized extension of OWL, let us

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

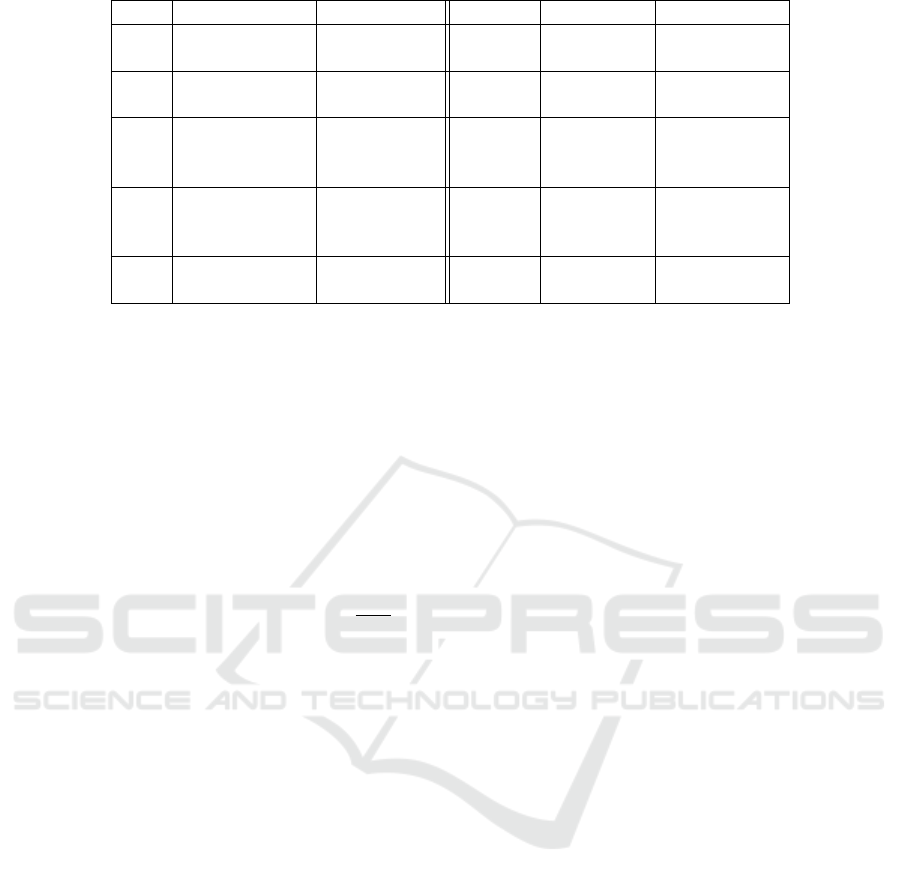
4 meaning conﬁdence belief disbelief uncertainty

! error

0 0.5 0.5 0

⊥ false [0,0] 0 1 0

E excluded [0,0.1] 0 0.9 0.1

U unlikely [0,0.3] 0 0.7 0.3

PN perhaps not [0.4,0.5] 0.4 0.5 0.1

FF ﬁfty-ﬁfty [0.45,0.55] 0.45 0.45 0.1

P perhaps [0.5,0.6] 0.5 0.4 0.1

N not excluded [0.1, 1] 0.3 0 0.7

L likely [0.7,1] 0.7 0 0.3

C conﬁrmed [0.9,1] 0.9 0 0.1

> true [1,1] 1 0 0

? unknown [0,1] 0 0 1

Figure 2: Representation of modal operators from 4 (incl. three in-the-middle modals) in terms of opinions in Subjective

Logic. The conﬁdence intervals for the ﬁve initial modals roughly coincide with the numbers depicted in Figure 1.

review here some of the work carried out in descrip-

tion logics. (Heinsohn, 1993) and (Jaeger, 1994) con-

sider uncertainty in ALC concept hierarchies, plus

concept typing of individuals (unary relations) in dif-

ferent ways (probability values vs. intervals; condi-

tional probabilities in TBox vs. TBox+ABox). They

do not address uncertain binary (or even n-ary) rela-

tions. (Tresp and Molitor, 1998) investigates vague-

ness in ALC concept descriptions to address state-

ments, such as the patient’s temperature is high, but

also for determining membership degree (38.5 °C).

This is achieved through membership manipulators

which are functions, returning a truth value between 0

and 1, thus deviating from a two-valued logic. (Strac-

cia, 2001) deﬁnes a fuzzy extension of ALC , based

on Zadeh’s Fuzzy Logic. As in (Tresp and Moli-

tor, 1998), the truth value of an assertion is replaced

by a membership value from [0, 1]. ALC assertions

α in (Straccia, 2001) are made fuzzy by writing,

e.g., hα ≥ ni, thus taking a single truth value from

[0,1]. An even more expressive theoretical descrip-

tion logic, Fuzzy OWL, based on OWL DL, is inves-

tigated in (Stoilos et al., 2005).

Our work might also be viewed as a modalized

version of a restricted fragment of Subjective Logic

(Jøsang, 1997; Jøsang, 2001), a probabilistic logic

that can be seen as an extension of Dempster-Shafer

belief theory (Wilson, 2000). Subjective Logic ad-

dresses subjective believes by requiring numerical

values for believe b, disbelieve d, and uncertainty u,

called (subjective) opinions. For each proposition, it

is required that b + d + u = 1.

The translation from modals δ to hb,d,ui is deter-

mined by the length of the conﬁdence interval µ(δ) =

[l,h] and its starting/ending numbers, viz., u := h − l,

b := l, and d := 1 − h (cf. Figure 2).

These deﬁnitions also address in-the-middle

modals (cf. footnote 3). Such modals even do not

need to be symmetrical, i.e., being around the center

of the conﬁdence interval. The deﬁnitions are clearly

not applicable to the error modal ! (cf. Section 5.1.7)

and it makes perfect sense to assume u = 0 here (re-

member, µ(!) =

0), and thus bisecting the belief mass

for this corner case, i.e., b = 0.5 and d = 0.5.

The simpliﬁcation and entailment rules of the for-

malism (Sections 4.1 and 5) allow rule-based (for-

ward) engines to easily implement this conservative

extension of OWL. Through these rules, the formal-

ism is compositional by nature and thus afﬂicted with

all the problems, reviewers have already noted on the

interplay between logic and uncertainty (Dubois and

Prade, 1994). Due to the ﬁnite number of modal oper-

ators, the approach is only able to approximately com-

pute the degree of uncertainty of new knowledge in-

stead of giving more precise estimations, by combin-

ing the low/high numbers of the conﬁdence intervals

through min/max, multiplication, addition, etc. Con-

trary to other approaches, we do not talk about the un-

certainty of complex propositions (conjunction, dis-

junction) or sets of beliefs, but instead focus merely

on the uncertainty of atomic ABox propositions.

ACKNOWLEDGEMENTS

The research described in this paper has been funded

by the German Federal Ministry of Education and

Research (BMBF) through the project HySocia-

Tea (Hybrid Social Teams for Long-Term Collab-

oration in Cyber-Physical Environments, grant no.

01IW14001). I have proﬁted from discussions with

my colleagues Miroslav Jan

cek, Bernd Kiefer, and

Stefan Schulz and would like to thank the ICAART

reviewers for their detailed and useful suggestions—

thank you guys!

Capturing Graded Knowledge and Uncertainty in a Modalized Fragment of OWL

REFERENCES

Areces, C., Hoffmann, G., and Denis, A. (2010). Modal

logics with counting. In Proceedings of the 17th Work-

shop on Logic, Language, Information and Computa-

tion (WoLLIC), pages 98–109.

Bishop, B., Kiryakov, A., Ognyanoff, D., Peikov, I., Tashev,

Z., and Velkov, R. (2011). OWLIM: A family of scal-

able semantic repositories. Semantic Web, 2(1):33–42.

Blackburn, P., de Rijke, M., and Venema, Y. (2001). Modal

Logic. Cambridge Tracts in Theoretical Computer

Science. Cambridge University Press, Cambridge.

Carroll, J. J., Dickinson, I., Dollin, C., Reynolds, D.,

Seaborne, A., and Wilkinson, K. (2004). Jena: Im-

plementing the Semantic Web recommendations. In

Proceedings of the 13th international World Wide Web

conference (WWW), pages 74–83.

Devlin, K. (2006). Situation theory and situation semantics.

In Gabbay, D. M. and Woods, J., editors, Handbook of

the History of Logic. Volume 7, pages 601–664. Else-

vier.

Dubois, D. and Prade, H. (1994). Can we enforce full com-

positionality in uncertainty calculi. In Proceedings

of the 12th National Conference on Artiﬁcial Intelli-

gence, pages 149–154.

Fine, K. (1972). In so many possible worlds. Notre Dame

Journal of Formal Logic, 13(4):516–520.

Golbreich, C. and Wallace, E. K. (2012). OWL 2 web ontol-

ogy language new features and rationale (second edi-

tion). Technical report, W3C.

Halpern, J. Y. (1990). An analysis of ﬁrst-order logics of

probability. Artiﬁcial Intelligence, 46:311–350.

Halpern, J. Y. (2003). Reasoning About Uncertainty. MIT

Press, Cambridge, MA.

Hayes, P. (2004). RDF semantics. Technical report, W3C.

Heinsohn, J. (1993). ALCP – Ein hybrider Ansatz zur

Modellierung von Unsicherheit in terminologischen

Logiken. PhD thesis, Universit

at des Saarlandes. In

German.

Jaeger, M. (1994). Probabilistic reasoning in terminological

logics. In Proceedings of the 4th International Confer-

ence on Principles of Knowledge Representation and

Reasoning (KR), pages 305–316.

Jøsang, A. (1997). Artiﬁcial reasoning with subjective

logic. In Proceedings of the 2nd Australian Workshop

on Commonsense Reasoning.

Jøsang, A. (2001). A logic for uncertain probabilities.

International Journal of Uncertainty, Fuzzyness and

Knowledge-Based Systems, 9(3):279–311.

Koller, D. and Friedmann, N. (2009). Probabilistic Graph-

ical Models. MIT Press.

Krengel, U. (2003). Einf

uhrung in die Wahrscheinlichkeits-

theorie und Statistik. Vieweg, 7th edition. In German.

Krieger, H.-U. (2012). A temporal extension of the

Hayes/ter Horst entailment rules and an alternative to

W3C’s n-ary relations. In Proceedings of the 7th In-

ternational Conference on Formal Ontology in Infor-

mation Systems (FOIS), pages 323–336.

Krieger, H.-U. (2013). An efﬁcient implementation of

equivalence relations in OWL via rule and query

rewriting. In Proceedings of the 7th IEEE Interna-

tional Conference on Semantic Computing (ICSC),

pages 260–263.

Lucas, P. J., van der Gaag, L. C., and Abu-Hanna, A. (2004).

Bayesian networks in biomedicine and health-care.

Artiﬁcial Intelligence in Medicine, 30:201–214.

Motik, B., Cuenca Grau, B., Horrocks, I., Wu, Z., Fokoue,

A., and Lutz, C. (2012). OWL 2 web ontology lan-

guage proﬁles. Technical report, W3C. W3C Recom-

mendation 11 December 2012.

Pearl, J. (1988). Probabilistic Reasoning in Intelligent Sys-

tems: Networks of Plausible Inference. Morgan Kauf-

mann, San Francisco, CA, MA.

Richardson, M. and Domingos, P. (2006). Markov logic

networks. Machine Learning, 62(1–2):107–136.

Schulz, S., Mart

ınez-Costa, C., Karlsson, D., Cornet, R.,

Brochhausen, M., and Rector, A. (2014). An onto-

logical analysis of reference in health record state-

ments. In Proceedings of the 8th International Con-

ference on Formal Ontology in Information Systems

(FOIS 2014).

Stoilos, G., Stamou, G. B., Tzouvaras, V., Pan, J. Z., and

Horrocks, I. (2005). Fuzzy OWL: uncertainty and

the semantic web. In Proceedings of the OWLED ’05

Workshop on OWL: Experiences and Directions.

Straccia, U. (2001). Reasoning within fuzzy description

logics. Journal of Artiﬁcial Intelligence Research,

14:147–176.

ter Horst, H. J. (2005). Completeness, decidability and

complexity of entailment for RDF Schema and a

semantic extension involving the OWL vocabulary.

Journal of Web Semantics, 3:79–115.

Tresp, C. B. and Molitor, R. (1998). A description logic

for vague knowledge. In Proceedings of the 13th Eu-

ropean Conference on Artiﬁcial Intelligence (ECAI),

pages 361–365.

Wikipedia (2015). Modal logic — Wikipedia, The Free En-

cyclopedia. [Online; accessed 19-June-2015].

Wilson, N. (2000). Algorithms for Dempster-Shafer theory.

In Algorithms for Uncertainty and Defeasible Reason-

ing, Handbook of Defeasible Reasoning and Uncer-

tainty Management Systems, pages 421–475. Kluwer.

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence