INFERENCE OF GENE REGULATORY NETWORKS BY

EXTENDED KALMAN FILTERING USING GENE EXPRESSION

TIME SERIES DATA

Ramouna Fouladi

, Emad Fatemizadeh

and S. Shahriar Arab

Department of Electrical Engineering, Sharif University of Technology, Azadi ave., Tehran, Iran

Department of Biophysics, Faculty of Biological Sciences, Tarbiat Modares University, Tehran, Iran

Keywords: Gene expression, Extended Kalman filtering, Gene regulatory network modelling.

Abstract: In this paper, the Extended Kalman filtering (EKF) approach has been used to infer gene regulatory

networks using time-series gene expression data. Gene expression values are considered stochastic

processes and the gene regulatory network, a dynamical nonlinear stochastic model. Using these values and

a modified Kalman filtering approach, the model’s parameters and consequently the interactions amongst

genes are predicted. In this paper, each gene-gene interaction is modeled using a linear term, a nonlinear

one, and a constant term. The linear and nonlinear term coefficients are included in the state vector together

with the gene expressions’ true values. Through the extended Kalman filtering process, these coefficients

are updated in such a way that the predicted gene expressions follow the ones observed. Finally,

connections between each two genes are inferred based on these coefficients.

1 INTRODUCTION

Gene expression is a process in which gene products

are synthesized using inherent information in genes.

Regarding different expression levels of different

genes in a cell, proteins present in the cell will vary

both in amount and the kinds. Thus, the cell can be

in different states, e.g. growth or death. Different

genes’ products can affect the rate of expression of a

specific gene in a direct or indirect way. Gene

Regulatory Networks map these interactions in the

form of a network. One of the important challenges

is the development of efficient algorithms to infer

these underlying connections using gene expression

time series data without performing complicated

time-consuming laboratory experiments.

One of the methods for modelling gene

expression data is dynamic modelling of gene

regulatory networks. Some of these models are

Boolean network models (Chen and Aihara, 1999);

(D'haeseleer et al., 1999); (Holter et al., 2001),

(Wang et al., 2008a), Bayesian model (Ghahramani,

1998); (Liu et al., 2006); (Murphy and Mian, 1999),

state space models ; (Rangel et al., 2004); (Wu et al.,

2004)) and stochastic model (Cook et al., 1998);

(Tian and Burrage, 2003); (Wang et al., 2008b).

Several factors should be considered in

proposing methods for modelling gene regulatory

networks. First of all, it is widely accepted that gene

expression is a stochastic process, so the model

defining the interactions should be able to handle the

stochastic nature of the network. Nonlinearity of the

interactions is another issue which should be taken

into account. In addition, gene regulatory networks

are usually a function of a large number of variables

but the available time series data only consists of a

small number of observations. Another issue is the

inherent noise in gene expression data due to the

nature of the process in which DNA microarray

experiments are performed. A comprehensive model

is the one which handles all these issues. Still, most

available methods in the literature have not

considered all. The use of extended Kalman filtering

seems to be a proper solution.

In this paper, gene expression values are

considered as stochastic processes .each gene-gene

interaction is modelled using a linear term, a

nonlinear one, and a constant term. The linear and

nonlinear term coefficients are included in the state

vector together with the gene expressions’ values.

Through the extended Kalman filtering process,

these coefficients are updated in such a way that the

150

Fouladi R., Fatemizadeh E. and Shahriar Arab S..

INFERENCE OF GENE REGULATORY NETWORKS BY EXTENDED KALMAN FILTERING USING GENE EXPRESSION TIME SERIES DATA.

DOI: 10.5220/0003754801500155

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 150-155

ISBN: 978-989-8425-90-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

predicted gene expressions follow the ones

observed. Finally, connections between each two

genes are inferred based on these predicted

coefficients. Four real-world gene expression data

sets are used to demonstrate the effectiveness of the

proposed algorithm.

The paper is organized as follows: section 2

describes the parameter estimation using EKF. Our

proposed method is discussed in section 3. The

experimental evaluation and discussions are given in

section 4, followed by conclusion and future works

in the final section.

2 PARAMETER ESTIMATION

USING EKF

In general, the nonlinear system dynamics and a

measurement are described by (Wang et al., 2009):

( 1) ((), ) ()

kfxk k





 

(1)

() ((), ) ()zk gxk vk





(2)

()k



and

()vk

are the process and measurement

noises which are assumed to be drawn from zero

mean multivariate normal distributions with

covariances.

and

respectively. These two

noises are two independent white noises.



is the

vector of the unknown parameters and is included in

the state vector

() [(), ()]

kxkk



 (3)

In order to use the Kalman or Extended Kalman

filters, some assumptions should be made.

Alongside the properties said for process and

measurement noises, we should assume Gaussian

probability distributions for the state variables. The

resulting dynamic equations are

(1) (()) ()

kFXkwk 

(4)

() ( ()) ()zk GX k vk

(5)

Where

() [ (),0]

wk k





(6)

( ()) [ ((), ()), ()]

TTT

Xk f xk k k





(7)

( ( )) ( ( ), ( ))GXk gxk k





(8)

Equations (4) and (5) serve as the state transition and

observation models respectively. Through a two

phase estimation process, the state vector is updated

in each step regarding the observations available.

A gene regulatory network containing

genes is

described by the following discrete-time nonlinear

stochastic dynamical system (Chen and Aihara,

1999), Where

identifies the linear regulatory

relationship between genes

and

identifies

the nonlinear relationship between genes

and

(1) () ((),)

( )

1, 2,..., 0,1, 2,..., 1

iijjijjjj

oi i

xk ax k bf x k

ink m







 







(9)

(, )

jj j









(10)

function

is a sigmoid function and is easily

differentiable. When a detailed description is

lacking, a sigmoid function is often used.

3 THE PROPOSED METHOD

In our algorithm, the model (9) is written for each

pair of genes in the network. So equation (9) for

genes 1 and 2 turns into:

11111221111

12 2 2 01 1

(1) () () (())

( ( )) ( )

kaxkaxkbfxk

bf xk I k









22112222111

22 2 2 02 2

(1) () () (())

( ( )) ( )

kaxkaxkbfxk

bfxk I k









(11)

Setting

11 2 2

( ( )) [ ( ( )), ( ( ))]

fxk fxk f x k

model (9)

can be written in vector form as follows:

(1) () (()) ()

k Axk Bf xk I k





 

(12)

() () ()

kxkvk





(13)

11 21 12 22

[, , , ]

Aaaaa





and

11 21 12 22

[, , , ]

Bbbbb





the vector of unknown parameters would be

[ ]

TTT







. Regarding equation (11), the

expression value of gene 1 at time step

is a linear

and a nonlinear function of the expression value of

the same gene at time-step

1k 

and a linear and

nonlinear function of the expression value of gene 2

at time-step



. In this paper, the coefficients

are set to zero in each time-step so that

each gene is bound to construct its expression values

at each time step from the expression values of the

other gene at the previous step, not its own. After

running the algorithm, we would have 4 time-series,

. For deducing the effect of gene 2

on gene 1, we first added up the absolute values of

INFERENCE OF GENE REGULATORY NETWORKS BY EXTENDED KALMAN FILTERING USING GENE

EXPRESSION TIME SERIES DATA

151

a and

b and then took an average over all time-

steps. The calculated number is indicative of the

strength of the regulatory influence of gene 2 on

gene 1. We did the same for finding the effect of

gene 1 on gene 2. After performing this process on

all pairs of genes, we would have an

nn

matrix (n

is the number of genes in the network), let’s call it

(, )

denotes the effect of gene

on gene

. The final interactions between genes are deduced

from the elements of the matrix

. By setting a

threshold, directed interactions would be inferred

based on these numbers. We should assert that in

each run of the algorithm (for each pair of genes),

the initial condition of the state vector and standard

deviation of the process and measurement noises are

kept constant so that the conditions are equal for all

cases.

The threshold is set in a way that at most

12%A

upper values of the elements of the matrix

are chosen. A is the percentile of true connections to

all possible connections. So, with an approximate

knowledge of the number of connections, nearly all

of them can be extracted by our method, See table 1.

Table 1: Threshold derivation based on percentile of real

interactions.

Data set name

percentile of

True

connections

percentile of

chosen

elements

Yeast Data Set 27.27% 25%

E-coli first Data Set 12.5% 18.75%

E-coli 2nd Data Set 51% 50%

IRMA (Switch on) 32% 44%

IRMA (Switch off) 32% 44%

4 RESULTS AND DISCUSSIONS

Our algorithm was evaluated and compared with

ARACNE (Margolin et al., 2006), TDARACNE

(Zoppoli et al., 2010), dynamical Bayesian Networks

implemented in the Banjo package (Yu et al., 2004)

and ODE implemented in the TSNI package (Bansal

et al., 2006), with gene expression data of yeast cell

cycle (Spellman et al., 1998), two SOS signalling

pathways in E. coli (Ronen et al., 2002); (Gardner,

2003) and an in vivo synthetic network, called

IRMA (Cantone et al., 2009).

The performance is measured in terms of

Positive Predictive Value (PPV), Recall and F-score.

PPV is the percentage of inferred connections which

are correct and Recall is the percentage of true

connections which are correctly inferred by the

algorithm. Suppose TP = number of True Positives,

FP = number of false positives and FN = number of

false negatives,

TP TP

PPV= Recall=

TP+FP TP+FN

The overall performance depends on both the PPV

and Recall. The F- score is the geometric mean of

PPV and Recall and is a good indicator of

performance:

2(PPV.Recall)

F-score

PPV+Recall



(14)

4.1 Yeast Data Set

Next, we selected an eleven gene network from

yeast S. Cerevisiae cell cycle.

Selected genes are Cln3, Cdc28, Mbp1, Swi4, Clb6,

Cdc6, Sic1, Swi6, Cln1, Cln2, and Clb5. Here the

cdc15 dataset was used as it has the maximum

number of gene expression measurements.After data

normalization and interpolation using cubic-spline

interpolation, the algorithm was run. The results

were evaluated using Pathway studio software and

summarized in Table 2.

Table 2: Comparison of our algorithm with previous methods. The displayed values are in percent.

Our method TD ARACNE TSNI BANJO

PPV Recall F-Score PPV Recall F-Score PPV Recall F-Score PPV Recall F-Score

Yeast Data set

41 38 39 41 22 29 29 19 23 43 28 34

E-coli SOS pathway (first data set)

33 50 40 85 75 80 13 25 17 18 38 24

IRMA network

Our Algorithm TD-ARACNE TSNI BANJO ARACNE

PPV Recall F-score PPV Recall F-score PPV Recall F-score PPV Recall F-score PPV Recall F-score

Switch-ON data

54 88 67 71 67 69 80 50 61 30 25 27 50 60 54

Switch-OFF data

55 75 63 37 60 46 60 38 46 60 38 46 25 33 28

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

152

Figure 1: Yeast cell cycle pathways in Pathway Studio and inferred by 4 algorithms; from top left to bottom right. Pathways

in Pathway Studio software, inferred graph by our algorithm, by TSNI, by TD-ARACNE, by Banjo. True connections are

shown with direct lines. The conections inferred with false direction are considered False positives and not displayed.

The network built by Pathway Studio Software and

the inferred network is displayed in Figure 1.The

color density of the lines define the number of

credible references acclaiming the connection. As

can be seen, our algorithm mostly recovers the most

confident interactions

4.2 e-Coli SOS Pathway (First Data

Set)

We also tested the proposed algorithm using eight

genes in E. coli SOS pathway. The SOS pathway is

activated in response to DNA damage in which the

cell cycle is arrested and DNA repair is induced. The

selected genes for this experiment are polB, uvrA,

lexA, uvrD, recA, uvrY, ruvA and umuDC. The

results are displayed in Table 2. The true network

and the inferred network are displayed in Figure 3.

4.3 e-Coli SOS Pathway (Second Data

Set)

We also tested the algorithm on nine other genes of

the SOS pathway in E-Coli. Selected genes are dinI,

rpoS, rpoD, umuDC, Ssb, recA, lexA, recF and

rpoH. We compared the network that we found with

the one that was identified in (Gardner, 2003) and

with a literature survey of the known interactions

among these nine genes (Fig. 2). Apart from self

feedbacks, the network has 43 connections. TSNI

algorithm could find 20 connections correctly

(Bansal et al., 2006) while NIR found 22

connections correctly out of 43 known connections.

We could predict 30 of the connections correctly

with PPV=69.7%, recall=71% and F-score=70%

Figure 2: Gene regulatory interactions between nine genes

of SOS network in E-Coli (second dataset) known in

literature. Positive effects are shown as line, and negative

ones as dashed lines.

4.4 IRMA Network

In (Cantone et al., 2009), a synthetic network was

built in the yeast Saccharomyces cerevisiae.

In this study, they tested the transcription of

network genes when culturing cells in galactose or

glucose. There are two sets of gene profiles, Switch

ON and Switch OFF. The first one corresponds to

shifting of the growing cells from glucose to

galactose and the second one corresponds to the

reverse shift. The inferred graph and true network

are displayed in Figure 4. The results are also

displayed in Table 2.

INFERENCE OF GENE REGULATORY NETWORKS BY EXTENDED KALMAN FILTERING USING GENE

EXPRESSION TIME SERIES DATA

153

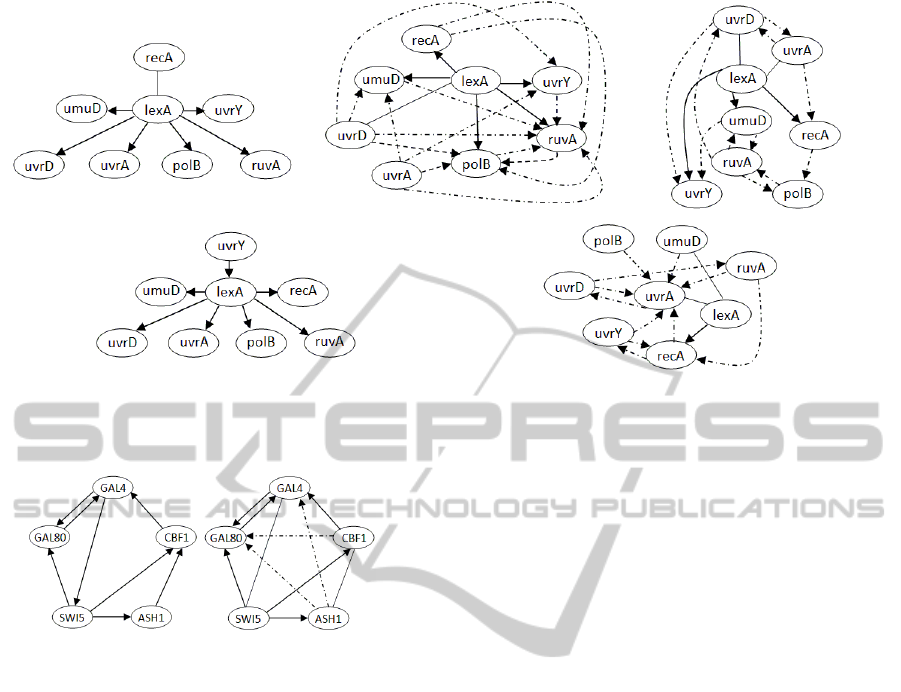
Figure 3: e-Coli SOS true pathway and inferred by 4 algorithms; from top left to bottom right, Original pathways, inferred

graph by our algorithm, by Banjo by TD-ARACNE, by TSNI. True positives are shown by direct lines and false positives

by dashed lines. Missing verse on the connection means that the algorithm recovers the wrong verse.

Figure 4: Left: Yeast synthetic network, right: network by

our algorithm (switch OFF dataset). Missing verse on the

connection means that the algorithm recovers wrong verse

As can be seen, in case of Yeast, we have a

considerable increase in Recall, which means the

proposed method can infer more of the true

interactions. It should be noted that this increase in

Recall not only hasn’t caused the PPV to decrease

but also has led to a larger F-Score. In case of the

first E-Coli dataset, PPV, Recall and F-Score have

increased considerably comparing the results of

TSNI and Banjo. In case of IRMA switch ON data,

PPV, Recall and F-score is greater than those of

ARACNE, Banjo and TSNI. Although the proposed

method has an F-Score almost equal to that of TD

ARACNE, the Recall value is greater. In case of

IRMA Switch OFF dataset, F-Score has an increase

around 20% compared to the best result by other

methods.

5 CONCLUSIONS

An algorithm was developed in this paper using

extended Kalman filtering. Results were good for

medium networks, but as said, the interactions are

deduced based on a two by two process. The

algorithm should be extended so that inference of

much larger networks is possible without much

computational cost. Using a clustering method prior

to running the algorithm and performing the

algorithm in each cluster separately seems a good

solution. In addition, in the expression profiles, only

the mRNA concentration is measured, while with

taking into account other biological data, better

results can be gained.

REFERENCES

Bansal, M., Della Gatta, G. and DI Bernardo, D., 2006.

Inference of Gene Regulatory Networks and

Compound Mode of Action from Time Course Gene

Expression Profiles. Bioinformatics, vol. 22, no. 7,

815-822.

Cantone, L., Marucci, L., Lorio, F., Ricci, M., Belcastro,

V., Bansal, M., Santini, S., DI Bernardo, M., DI

Bernardo, D. and Cosma, M., 2009. A Yeast Synthetic

Network for In Vivo Assesment of Reverse-

Engineering and Modeling Approaches. Cell, 137,

172-181.

Chen, T. and Aihara, K. Year. Modeling Gene Expression

with Differential Equations. In: proc. pacific symp.

Biocomputing, 1999. 29-40.

Cook, D. L., Gerber, A. N. and Tapscott, S. J. Year.

Modeling Stochastic Gene Expression: Implications

for Haploinsufficiency. In: Proc. Nat'l Academy of

Science, USA, 1998. 15641-15646.

D'haeseleer, P., Wen, X., Fuhrman, S. and SOMOGYI, R.

Year. "Linear Modeling of mRNA Expression Levels

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

154

during CNS Development and Injury,". In: Proc.

Pacific Symp. Biocomputing, 1999. 41-52.

Gardner, T. 2003. Inferring genetic networks and

identifying compound mode of action via expression

profiling. Science, vol. 301, 102-105.

Ghahramani, Z. 1998. Learning Dynamic Bayesian

Networks. Adaptive Processing of Sequences and

Data Structures, Springer-Verlag, 168-197.

Holter, N. S., Maritanm, A., Cieplak, M., Fedoroff, N. V.

and Banavar, J. R. 2001. "Dynamic Modeling of Gene

Expression Data,". Proc. Nat'l Academy of Science.

USA.

Liu, T., Sung, W. and Mittal, A. 2006. Model Gene

Network by Semi-Fixed Bayesian Network. Expert

Systems with Applications, vol. 30, no.1, 42-49.

Margolin, A. A., Nemenman, I., Basso, K., Wiggins, C.,

Stolovitzky, G., Dalla Favera, R. and Califano, A.

2006. ARACNE: an algorithm for the reconstruction

of gene regulatory networks in a mammalian cellular

context. BMC Bioinformatics, 7 Suppl 1, S7.

Murphy, K. and Mian, S. 1999. Modeling Gene

Expression Data Using Dynamic Bayesian Networks.

technical report, Univ. of California.

Rangel, C., Angus, J., Ghahramani, Z., Lioumi, M.,

Sotheran, E. A., Gaiba, A., Wild, D. L. and Falciani,

F. 2004. Modeling T-Cell Activation Using Gene

Expression Profiling and State Space Models.

Bioinformatics, vol. 20, no. 9, 1361-1372.

Ronen, M., Rosenberg, R., Shraiman, B. and Alon, U.

Year. Assigning Numbers to the Arrows:

Parameterizing a Gene Regulation Network by Using

Accurate Expression Kinetics. In: Proc Nat'l Academy

Science, USA, 2002. 10555-10560.

Spellman, P., Sherlock, G., Zhang, M., Iyer, V., Anders,

K., Eisen, M., Brown, P., Botsein, D. and B, F. 1998.

Comprehensive Identification of Cell Cycleregulated

Genes of the Yeast Saccharomyces cerevisiae by

Microarray Hybridization. Molecular Biology of the

Cell, vol. 9, no. 12, 3273-3297.

Tian, T. and Burrage, K. Year. Stochastic Neural Network

Models for Gene Regulatory Networks. In: Proc. 2003

IEEE Congress Evolutionary Computation, 2003. 162-

169.

Wang, Z., Gao, H., Cao, J. and Liu, X., 2008a. “On

Delayed Genetic Regulatory Networks with Polytopic

Uncertainties: Robust Stability Analysis,”. IEEE

Trans. NanoBioscience, vol. 7, no. 2, 154-163.

Wang, Z., Liu, X., Liang, J. and Vinciotti, V., 2009. An

Extended Kalman Filtering Approach to Modeling

Nonlinear Dynamic Gene Regulatory Networks via

Short Gene Expression Time Series. IEEE/ACM

Transactions on Computational Biology and

BioinformaticS, vol. 6, no. 3, 410-419.

Wang, Z., Yang, F., Ho, D. W. C., Swift, S., Tucker, A.

and Liu, X. 2008b. Stochastic Dynamic Modeling of

Short Gene Expression Time Series Data. IEEE Trans.

NanoBioscience, vol. 7, no. 1, 44-55.

Wu, F., Zhang, W. and Kusalik, A. J. Year. Modeling

Gene Expression from Microarray Expression Data

with State-Space Equations. In: Proc. Pacific Symp.

Biocomputing, 2004. 581-592.

Yu, J., Smith, V., Wang, P. and Hartemink, A. 2004.

Advances to Bayesian Network Inference for

Generating Causal Networks from Observational

Biological Data. Bioinformatics, vol. 20, no. 18, 3594-

3603.

Zoppoli, P., Morganella, S. and Ceccarelli, M. 2010.

TimeDelay-ARACNE: Reverse engineering of gene

networks from time-course data by an information

theoretic approach. BMC Bioinformatics, 11, 154.

INFERENCE OF GENE REGULATORY NETWORKS BY EXTENDED KALMAN FILTERING USING GENE

EXPRESSION TIME SERIES DATA

155