MEAN FIELD MONTE CARLO STUDIES
OF ASSOCIATIVE MEMORY
Understanding the Dynamics of a Many-pattern Model
Ish Dhand
1
and Manoranjan P. Singh
2
1
Department of Computer Science and Engineering, Indian Institute of Technology Kanpur, 208016 Kanpur, India
2
Laser Physics Division, Raja Ramanna Center for Advanced Technology, 452013 Indore, India
Keywords:
Associative memory, Spin system.
Abstract:
Dynamics of a Hebbian model of associative memory is studied using Mean field Monte-Carlo method. Under
the assumption of infinite system, we have derived single-spin equations, using the generating functional
method from statistical mechanics, for the purpose of simulations. This approach circumvents the strong
finite-size effects of the usual calculations on this system. We have tried to understand the retrieval of a stored
pattern in presence of another condensed pattern undergoing reinforcement, positive or negative. We find that
the retrieval is faster and the retrieval quality is better for the case of positive reinforcement.
1 INTRODUCTION
In the theoretical study of the neural network repre-
sentation of associative memory, models composed
of spin-like elements play an important role. In most
simple cases, two state (Ising-Spin) variables are used
to model the basic processing elements i.e. neurons
(Hopfield, 1982). The dynamics of this system is de-
scribed by update rules that specify the behavior of
the state of the neuron (spin) as governed by the net
synaptic input (local field at the spin) from the other
neurons in the network. These interactions between
the neurons are obtained from the employed learning
rule and are represented in the synaptic matrix. To
analyze the retrieval performance such as speed and
quality of retrieval of the network, it is necessary to
use dynamical techniques from non equilibrium sta-
tistical physics (as opposed to methods from equilib-
rium statistical physics). Another feature characteris-
tic of biological systems which neccessitates the use
of dynamical methods is asymmetry in the couplings
i.e. J
i j
6= J
ji
where J
i j
is the interaction strength be-
tween i
th
and j
th
neurons (Amit, 1992).
In the direct numerical simulations done within
the above scheme, N
2
couplings have to be stored
for a connected model where N is the total number
of neurons. This makes the task of extrapolation from
a finite number of spins to the Large N (thermody-
namic) limit a highly non-trivial one (Kohring and Sc-
hreckenberg, 1991). Thus, to understand the be-
haviour of macroscopic quantities, like suitably de-
fined order parameters, of large networks, it is rele-
vant to use fully connected models for which a dy-
namical mean field theory can be formulated for an
infinite system. This technique was implemented
by (Eissfeller and Opper, 1992) who used the gen-
erating functional technique to develop a numerical
method for analyzing the dynamics of a system con-
sisting of interactions in the Sherrington-Kirkpatrick
(SK) model for spin glasses (Sherrington and Kirk-
patrick, 1975). In their work, the generating func-
tional method was employed to derive stochastic
single-spin dynamical rules in the large-N limit and
this self-consistent single spin dynamics is simulated
using a Monte Carlo Procedure to calculate disorder
averaged quantities. The same method was gainfully
used by (Singh and Dasgupta, 2003) to study the dy-
namics of pattern retrieval in a Hopfield-like model
of associative memory with one stored pattern. While
discussing the possible relevance of this one pattern
model for the Hopfield-like models, it was argued
the pattern stored in the network represents the con-
densed pattern the network is trying to recall. The ef-
fect of the other uncondensed pattern is mimicked by
the SK model like coupling term in the synaptic ma-
trix. It is natural to ask as to what happens to the re-
call process when there are other condensed patterns.
This could correspond to the physical situation when
395
Dhand I. and P. Singh M..
MEAN FIELD MONTE CARLO STUDIES OF ASSOCIATIVE MEMORY - Understanding the Dynamics of a Many-pattern Model.
DOI: 10.5220/0003683803950400
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 395-400
ISBN: 978-989-8425-84-3
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

other patterns are recollected (with a positive acqui-
sition strength) or forgotten (with a negative acqisi-
tion strength). In an attempt to answer this question
we generalize the method for the two patterns (further
generalization for more than two patterns is straight-
forward).
The present work focuses on a neural network
model of associative memory with two binary pat-
terns. The synaptic matrix consists of two parts – one
corresponding to the Hebbian learning (Hebb, 2002)
of the patterns with respective acquisition strengths
and the other corresponding to the coupling matrix
of SK model. We oncentrate on the retrieval dynam-
ics of the one of the stored patterns. The SK part in
the synaptic matrix may effectively mimick the in-
terference from a macroscopic number (of the order
of number of neurons) ‘other’ uncondensed memo-
ries when the connection between this simple model
and the Hopfield like models is sought. In this frame-
work, we can understand the effect of interference due
to specific condensed patterns (those having a finite
macroscopic overlap with the pattern under consider-
ation) as opposed to just the interference from a large
number of uncondensed (not having any macroscopic
overlap with the initial pattern) patterns. We present
the generating functional treatment used to derive the
self-consistent stochastic dynamical rules and the re-
sults of the Monte-Carlo Simulation of the subsequent
single-spin dynamics.
The paper is organized as follows: Section 2 de-
scribes, in detail, the model under consideration. In
Section 3, we discuss the derivation of the Single Spin
Equations in the Large N limit. Section 4 details the
method used to simulate the single spin equation. We
conclude with results and discussions in Section 5.
2 ASYMMETRIC SK MODEL
WITH MULTIPLE PATTERNS
2.1 The Neurons and their Interaction
The model network is composed of N two-state neu-
rons (Ising Spins) σ
i
= ±1. Every neuron σ
i
is inter-
acting with all other neurons σ
j
by couplings J
i j
:
J
i j
= J
SK
i j
+
J
1
N
ξ
1
i
ξ
1
j
+
J
2
N
ξ
2
i
ξ
2
j
+..., i 6= j , J
ii
= 0,
(1)
The first term represents the couplings in the SK
Model with Random Asymmetric Interactions. This
can be taken as the two (multi) pattern analogue of
the tabula non rasa scenario proposed by Toulouse,
Dehaene, and Changeux (Toulouse et al., 1986). The
terms that follow it represent Hebbian Learning of
memory patterns ξ
1
i
,ξ
2
i
,... with J
1
,J
2
,... are the re-
spective acquisition strengths for the patterns. The
couplings J
SK
i j
are independent Gaussian random vari-
ables for all i < j and are drawn from the distribution:
P

J
SK
i j

=
s
1
2π/N
exp





−

J
SK
i j

2
2/N





, i < j .
(2)
The information about the symmetry of the coupling
matrix is expressed in terms of η, the average symme-
try parameter:

J
SK
i j
J
SK
ji

= η/N , (3)
The Brackets, here, denote the (ensemble) average
over the distribution of couplings. The values η = 1
and η = −1 correspond to symmetric couplings and
fully antisymmetric couplings respectively. The case
η = 0 denotes totally uncorrelated couplings. Cou-
plings with the average symmetry η can be con-
structed via[]
J
SK
i j
=

1 + η
2

1/2
J
s
i j
+

1 − η
2

1/2
J
as
i j
, (4)
Here, J
s
i j
(= J
s
ji
) and J
as
i j
(= −J
as
ji
), the symmetric and
the antisymmetric components of the SK interaction,
are independent Gaussian random variables, for all
i < j, and are drawn from the same distribution as that
in Eq. (2). However for all the results reported here
we have considered only the symmetrical couplings.
The effect of asymmetry will be taken up elsewhere.
2.2 The Dynamical Rule
In this work, we consider the noise-free (Zero Tem-
perature) dynamics of the system with a synchronous
update of all the spins as a response to the local field
h
i
(t) acting on each spin σ
i
. At any elementary time
step t, the update rule is given by:
σ
i
(t +1) = sgn (h
i
(t)) , i = 1,...,N, (5)
Where
h
i
(t) =
∑
j6=i
J
i j
σ
j
(t),
=
h
1+η
2
i
1/2
∑
j6=i
J
s
i j
σ
j
(t) +
h
1−η
2
i
1/2
∑
j6=i
J
as
i j
σ
j
(t) +
J
1
N
ξ
1
i
ξ
1
j
+
J
2
N
ξ
2
i
ξ
2
j
+ ... . (6)
The first term plays the role of the noise due to the in-
terference from a large number (Finite fraction of the
number of neurons) of patterns stored in the network.
NCTA 2011 - International Conference on Neural Computation Theory and Applications
396

The second one is the antisymmetric term from the
synaptic matrix. The terms following that correspond
to the pattern under retrieval and the interference term
due to the other condensed pattern.
2.3 Assessing the Retrieval Properties
In this paper, we aim to assess the retrieval proper-
ties of a network of associative memory with more
than one condensed memories. We shall work in the
framework of an initial value problem, in which the
initial (t = 0) neural network configuration, {σ
i
(0)},
has an overlap m
k
with the stored pattern ξ
k
i
. The evo-
lution of the system to a state that has overlap m
l
with
a stored pattern ξ
l
i
that is sufficiently close to unity is
referred to as the successful of the latter pattern. In
the presence of interference from an additional con-
densed pattern, the following quantities are of partic-
ular concern:
1. Retrieval quality, i.e., the degree of closeness of
the final state to the relevant pattern under re-
trieval.
2. Convergence time, i.e., time taken by the neural
network to converge to a final state close to the
corresponding stored pattern.
The simulation is done on self-consistent single-spin
dynamics that is obtained using the Dynamical Mean
Field Theory described in the following section.
3 DYNAMICAL MEAN FIELD
THEORY
Under the assumption that each spin is coupled to
all the other spins we shall show that the internal
field, h
i
(t), which depends explicitly on the states of
all the spins, can be replaced by an effective ‘mean
field’ which depends only on some macroscopic or-
der parameters. This effective internal field is a time-
dependent random process and is different from the
averaged internal field [h
i
(t)]. The random processes
for effective field h
i
(t) can be constructed conve-
niently using the Dynamical Generating Functional
technique. This effective field can be used to generate
stochastic spin trajectories in a monte-carlo simula-
tion.
We are interested in the statistical properties of a
large, but finite number N
T
of spin trajectories over
t
f
time steps, at the sites i = 1,. . . , N
T
, out of a sys-
tem in which the total number of spins, N, may be
very large. To derive these properties, we consider
the dynamical generating function
h
Z(l)
i
J
for the lo-
cal fields h
i
(t), i = 1,...,N
T
; t = 1,. . . ,t
f
in a system
with just 2 patterns:
hZ(l)i
J
= hTr
σ(t)
R
∏
N
i=1
∏
t
f
t=1
{h
i
(t)Θ(σ
i
(t +1)
h
i
(t)) × δ(h
i
(t) − [
1+η
2
]
1/2
∑
j6=i
J
s
i j
σ
j
(t) +
h
1−η
2
i
1/2
∑
j6=i
J
as
i j
σ
j
(t) +
J
1
N
ξ
1
i
ξ
1
j
+
J
2
N
ξ
2
i
ξ
2
j
)}
×exp(
∑
t
f
t=0
∑
N
T
i=1
l
i
(t)h
i
(t))i
J
. (7)
Here, h···i
J
represents the average over the all possi-
ble random couplings and Tr
σ
denotes the sum over
all 2
N t
f
possible states of the spin-system, σ
i
(t) = ±1.
θ(x) and δ(x) are the unit step function and the dirac
delta function respectively. These functions ensure
that only those ‘spin paths’ σ
i
(t) which are consistent
with the equations of motion (5) and (6)contribute to
h
Z(l)
i
J
.
The calculation of
h
Z(l)
i
J
follows, closely, the
derivation given in (Eissfeller and Opper, 1994) (for
the asynchronous case with J
0
= 0), which in turn is a
generalization of the derivation given by (Henkel and
Opper, 1991) for the synchronous dynamics of a neu-
ral network. Analysis showed us that in the large-N
limit, the generating function can be completely fac-
torised into independent components for the N
T
spins:
h
Z(l)
i
J
∝
∏
N
T
i=1
D
Tr
σ
i
(t)
R
∏
t
{
dh
i
(t)Θ (σ
i
(t + 1)
h
i
(t))
}
exp
{
i
∑
t
l
i
(t)h
i
(t)
}
∏
t
δ

h
i
(t)− J
1
m
1
(t)ξ
2
i
−J
2
m
2
(t)ξ
2
i
− φ
i
(t)− η
∑
s
K(t,s)σ
i
(s)

φ
. (8)
In this form of the generating function, we see that
the dynamics of the spin system is described by the
uncorrelated system of dynamical equations:
σ
i
(t +1) = sign (h
i
(t)) , (9)
where
h
i
(t) = J
1
m
1
(t)ξ
1
i
+ J
2
m
2
(t)ξ
2
i
+ φ
i
(t) +
η
∑
s<t
K(t,s)σ
i
(s). (10)
We have effectively replaced the time-independent
random couplings to other spins by a Gaussian ran-
dom variables φ
i
(t), with zero mean and covariance
h
φ
i
(t)φ
i
(s)
i
φ
= C(t, s), introduced independently for
each site i. In the above equation (Eq. 10),the first two
terms in the above ‘effective’ local field come from
the mean field theory and are responsible pattern re-
trieval, the third term is a Gaussian noise, while the
fourth term represents a retarded self-interaction.
The order parameters can be rewritten in terms of
the Gaussian averages:
C(t,s) =
h
φ(t)φ(s)
i
φ
=
h
σ(t)σ(s)
i
φ
, (11)
K(t,s) = −i

ˆ
h(s)σ(t)

φ
=

∂
∂φ(s)
σ(t)

φ
.(12)
MEAN FIELD MONTE CARLO STUDIES OF ASSOCIATIVE MEMORY - Understanding the Dynamics of a
Many-pattern Model
397

From Eq. (12) we can physically interpret K(t,s) as a
response function. In order to evaluate it, we express
the above average of the partial derivative in terms
of the correlation function hσ(t)φ(s)i using a discrete
version of Novikov’s theorem (Hanggi, 1978).
hσ(t)φ(s)i =
t
∑
τ=0
K(t,τ)C(τ,s) . (13)
4 RESULTS: RETRIEVAL
PROPERTIES
4.1 Method: The Monte Carlo
Simulations
We have used the effective single-spin equations, (9)
and (10) to calculate the exact averages in the N → ∞
limit. To carry this out, spin variables have been ex-
pressed as explicit functions of the Gaussian Fields
and integrations (weighted by the multivariate Gaus-
sian) have been performed by a Monte-Carlo pro-
cess. At each time step, the necessary averages over
the system (of N → ∞ spins) have been calculated
by summing over a system of large number (N
T
) of
single-spin trajectories.
To reduce the numerical errors of the Monte-Carlo
integration, we have used N
t
= 2.5 × 10
6
. Simula-
tions over time scales of t
f
= 100 time steps can safely
be carried out neglecting the error propagation effect
from imperfections in the Gaussian random distribu-
tion used.
We have investigated the effect of an additional
condensed pattern on the retrieval properties (includ-
ing time and quality of retrieval) of a system. The
additional condensed pattern may have a positive cou-
pling strength (as in the case of retrieval of the mem-
ory) or negative (corresponding to the process of for-
getting of a memory).
4.2 The Evolution of Overlap with the
Stored Pattern
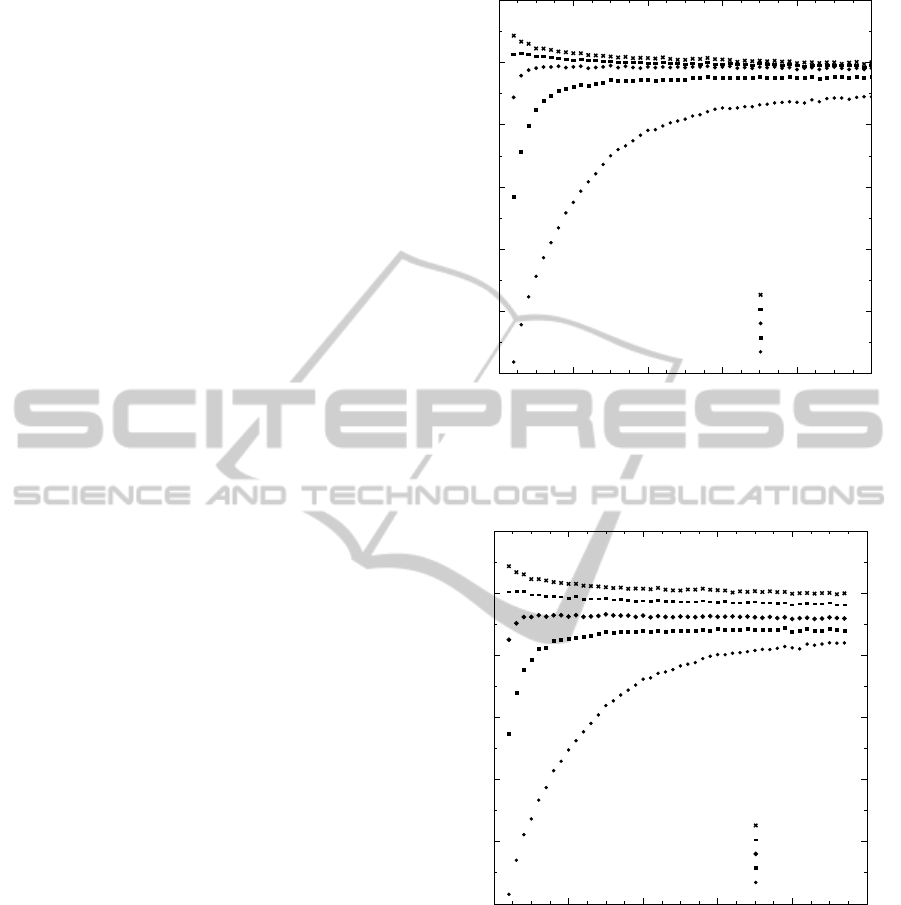
Figures 1 and 2 show the time evolution of the over-
lap of the current state of the system with the respec-
tive stored pattern. While Fig. 1 refers to a system
which is simultaneously in the process of recollecting
another memory (with coupling strength (J
1
= 0.6),
Fig. 2 corresponds to a the negative recollection
(J
1
= −0.6) or (forgetting of the second memory. The
different curves represent different strength of the ini-
tial overlap of the system with the two memory pat-
terns.


46(


46(


46(


46(


46(


46







     
Figure 1: Value of overlap of pattern at time t with one
condensed pattern (with coupling strength J
0
= 1.5) in pres-
ence of another pattern which has Positive coupling strength
(J
1
= 0.6).


46(


46(


46(


46(


46(


46







     
Figure 2: Value of overlap of pattern at time t with one con-
densed pattern (with coupling strength J
0
= 1.5) in presence
of another pattern which has negative coupling strength
(J
1
= −0.6).
The following function fits the above results very
well:
m(t) = m
∞
+ const ×t
−a
exp(−t/τ). (14)
Here, m
∞
is a measure of the quality of retrieval and τ
and a describe the speed of retrieval of the memory.
NCTA 2011 - International Conference on Neural Computation Theory and Applications
398

4.3 Speed of Retrieval
Figure 3 shows ratio of time of retrieval for addi-
tional coupling negative (J
1
= −0.6) to additional
coupling positive (J
1
= 0.6) as it varies with initial
overlap of the system with the additional stored pat-
tern m
1
(t = 0). For small values of starting overlap
with the additional memory, the case with recolection
is faster than the one with forgetting of an additional
stored pattern.
ttttttt
-
rnJ=1Pvttt
-
rn=1Pvt
=
-
0
.
6
)
P
 t!"tt#t$%t&& t&t t
-
rn=v
= =10 =16 =1P =12 -
Figure 3: Variation of Ratio of time of retrieval for addi-
tional coupling negative (J
1
= −0.6) to additional coupling
positive (J
1
= 0.6) w.r.t. initial overlap of the system with
the additional stored pattern m
1
(t = 0).
4.4 The Quality of Retrieval
Figure 4 shows the difference between the quality of
retrieval of a stored pattern for the cases of positve and
negative coupling of additional pattern. In the model
under consideration, it is clear that the presence of an
additional memory which is being recollected leads to
better retrieval quality.
5 CONCLUSIONS
We have studied the dynamics of associative memory
using mean field Monte-Carlo method. In the case
of an infinite system, we have derived and simulated
single-spin dynamical equations. We find that the re-
trieval is faster and the retrieval quality is better in
case another stored memory is being recollected as
compared to the case in which another stored mem-
ory is being forgotten.

t
f wrg

t
f ewrg
      
wr7h
wr7s
wr7g
wr72
wr2
        
t
nfwa
w wrh wrs wrg wr2
Figure 4: Quality of retrieval of the final stored pattern w.r.t.
initial overlap of the system with the additional stored pat-
tern m
1
(t = 0).
ACKNOWLEDGEMENTS
This work was supported by the National Initia-
tive on Undergraduate Sciences (NIUS) undertaken
by the Homi Bhabha Centre for Science Education
(HBCSE-TIFR), Mumbai, India. We thank Prof. Vi-
jay Singh for helpful discussions.
REFERENCES
Amit, D. J. (1992). Modeling Brain Function: The World
of Attractor Neural Networks. Cambridge University
Press.
Eissfeller, H. and Opper, M. (1992). New method for
studying the dynamics of disordered spin systems
without finite-size effects. Physical Review Letters,
68(13):2094.
Eissfeller, H. and Opper, M. (1994). Mean-field monte carlo
approach to the Sherrington-Kirkpatrick model with
asymmetric couplings. Physical Review E, 50(2):709.
Hanggi, P. (1978). Correlation functions and masterequa-
tions of generalized (non-Markovian) langevin equa-
tions. Zeitschrift fr Physik B Condensed Matter and
Quanta, 31(4):407–416.
Hebb, D. O. (2002). The organization of behavior: a neu-
ropsychological theory. L. Erlbaum Associates.
Henkel, R. D. and Opper, M. (1991). Parallel dynamics of
the neural network with the pseudoinverse coupling
matrix. Journal of Physics A: Mathematical and Gen-
eral, 24(9):2201–2218.
MEAN FIELD MONTE CARLO STUDIES OF ASSOCIATIVE MEMORY - Understanding the Dynamics of a
Many-pattern Model
399

Hopfield, J. J. (1982). Neural networks and physical sys-
tems with emergent collective computational abilities.
Proceedings of the National Academy of Sciences,
79(8):2554 –2558.
Kohring, G. and Schreckenberg, M. (1991). Numerical
studies of the spin-flip dynamics in the SK-model.
Journal de Physique I, 1(8):5.
Sherrington, D. and Kirkpatrick, S. (1975). Solvable
model of a Spin-Glass. Physical Review Letters,
35(26):1792.
Singh, M. P. and Dasgupta, C. (2003). Mean-field monte
carlo approach to the dynamics of a one pattern model
of associative memory. cond-mat/0303061.
Toulouse, G., Dehaene, S., and Changeux, J. P. (1986). Spin
glass model of learning by selection. Proceedings of
the National Academy of Sciences, 83(6):1695 –1698.
NCTA 2011 - International Conference on Neural Computation Theory and Applications
400