
DEVELOPING COMBINED FORECASTING MODELS
IN OIL INDUSTRY
A Case Study in Opec Oil Demand
Seyed Hamid Khodadad Hosseini
1
, Adel Azar
1
, ALi Rajabzadeh Ghatari
1
and Arash Bahrammirzaee
2
1
Department of Management, Tarbiat Modares University (TMU), Tehran, Iran
2
Iran Management and Productivity Center Researcher, Tehran, Iran
Keywords: Energy forecasting, Neural network forecasting, Combined forecasting, Oil demand.
Abstract: The purpose of this research is to study the combined forecasting methods in energy section. This method is
a new approach which leads to considerable reduction of error in forecasting results. In this study,
forecasting has been done through using individual methods (these methods consist of exponential
smoothing methods, trend analysis, box-Jenkins, causal analysis, and neural network models) and also
combining methods. In next step, the Results of these individual forecasting methods have been combined
and compared with artificial neural networks, and multiple regression models. The data we used in this
study are: dependent variable: OPEC oil demands from 1960 to 2005, and independent variables: oil price,
GDP, other energy demands, population, and added-value in industry (in OECD countries. Computed
indexes of errors are: MSE, MAPE, and GAPE which show considerable reductions in the errors of
forecasting when using combining models. Therefore, it is suggested that the designed models could be
applied for oil demand forecasting.
1 INTRODUCTION
Decision making about energy and other related
problems in our chaotic world is a crucial issue for
managers at national level, and also for large,
middle, and small enterprises. Any changes in
energy consumption rate considerably influence
related decisions and plans. Due to numerous
variables in this area, managers and experts prefer to
have some mechanisms to help them make
appropriate decisions. Forecasting OPEC
(Organization of Petroleum Exporting Countries)
crude oil demand is a relatively difficult task which
represents two essential attributes: on the one hand,
it shows the strong daily changes and on the other, it
clearly shows the increasing trend. Mostly, the
prediction of oil industry is based on time series
analysis. Time series methods are affected by other
variations that make the problem hard to model.
Some of the researchers aimed to propose models
which consider affective factors on crude oil
(Medlock and Ronald, 1999). Factors, such as the
rate of population change, industrial growth or
decline, the added value of industry, government
regulations, and energy-thrift policies have been
identified as effective items on energy demand
changes (Schrattenholzer, 2004). Therefore, a
complex model, taking into account the effects of
these individual parameters, might seem to be
necessary when predicting energy-demand changes
(Mackay and Probert, 2001).
The conventional time series modeling methods
have served the scientific community for a long
time; however, they provide only reasonable
accuracy and suffer from the assumptions of
stationary and linearity. Among the traditional
model, one of the most important and widely used
time series models is the autoregressive integrated
moving average (ARIMA). The popularity of the
ARIMA model is due to its statistical properties as
well as the well-known Box–Jenkins methodology
(Box and Pierce, 1970).
Among new methods, Artificial Neural Networks
(ANNs) are considered as efficient tools for
modeling and forecasting during the last two
decades. The major advantage of neural networks is
their flexible nonlinear modeling capability. With
ANNs, there is no need to specify a particular model
form. Rather, the model is adaptively formed based
205
Khodadad Hosseini S., Azar A., Rajabzadeh Ghatari A. and Bahrammirzaee A..
DEVELOPING COMBINED FORECASTING MODELS IN OIL INDUSTRY - A Case Study in Opec Oil Demand.
DOI: 10.5220/0003681702050210
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 205-210
ISBN: 978-989-8425-84-3
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

on the features presented from the data (Zhang et al.,
2001).
However, there are extensive researches in
forecasting domain, especially in financial domain
(Bahrammirzaee, 2010), but a few researches have
been conducted on oil demand predictions using
intelligent techniques (e.g., Assareh et al., 2010).
This shortage makes much more sense in a country
like Iran with huge oil consumption, and therefore
demands. This issue is central focus point of this
article. In the next section, the process of selection
of variable, sample, and data gathering will be
detailed.
This paper is organized as follows: first, based
on previous researches and also documented OPEC
crude oil studies, the affected variables are selected.
The prediction has been done separately by classic
methods and ANN algorithm, and then the combined
methods is suggested for such a prediction.
2 VARIABLES, SAMPLE AND
DATA GATHERING
Most of the oil market studies are based on classic
forecasting methods. For example, in 2007,
(Dochuchaev, 2007) have done a research on
effective factors in oil and demand price by studying
structure’s evolution and price revolutions. The
research of (Petrov et al., 2004), introduce some
effective factors such as political factors.
The variables which have been extracted based
on extensive review of researches (Oil Market
Report, 1993-2005); (OPEC Annual Bulletin, 2000);
(OPEC Oil and Energy Data, 1980-2005); (Arab Oil
and Gas Directory,1985-2005). are as follows:
1. Crude oil price.
2. Income of the countries which are consumers of
OPEC oil, namely members of OECD. (GDP and
economic growth).
3. The population level and the population growth
rate of OECD countries.
4. Other kinds of energy consumption, e.g. gas,
electrical energy, nuclear energy.
5. The Added-Value of the industrial sector of
OECD countries.
As cited before, these variables have been selected
based on the literature review which has been done
by authors, but because of the limited related studies
in this area, we tried to extend these factors by
taking expert’s opinions acquisition. For formulating
variables, designing check lists using Delphi
methods is done. Delphi method is used for
minimizing deviation among the experts. After
determining these variables, the related data sets
consisting of OPEC oil demand rates from 1960 to
2005, as dependent variable and price, GDP,
population, added- value in industry and other
demands for energy, as independent variables are
obtained. Data acquired from 1960 to 1996 were
used as sample data, and from 1997-2005 as testing
data.
Methods used in this research for forecasting are
quantitative methods. These methods include time-
series analysis (mono-variable analysis including
exponential smoothing, trends analysis, Box-
Jenkins) and causal analysis (econometric, ANN).
These methods which are called individual methods
are used for predicting oil demand, and then these
methods are combined. The combination is done by
neural network, multiple regression, and sequential
methods.
3 MODELING AND DATA
ANALYSIS
The following separated steps are done for modeling
the crude oil demand prediction:
Step 1: Forecasting Oil Demand using Classic
Methods: We used classic methods and their
analyses as follows:
1. Exponential Smoothing Forecasting Methods:
This method includes some separated forecasting
such as:
Simple Brown: This is a forecasting method using
an adjustment coefficient which reduces forecasting
errors. After analyzing this data driven method, the
smoothing coefficient was equal to 0.1 (α= 0.1).
This amount is computed by trial and error and takes
the best result for the sum of the square of errors.
Holt Smoothing Method: This method also predicts
through an adjustment coefficient which reduces
forecasting errors. After analyzing this method, the
smoothing coefficient was equal to 0.7 (α= 0.1) and
β (trend coefficient) equal to 0.4.
This amount is computed by trial and error which
takes the minimum amount of the sum of the square
of errors.
Custom Smoothing with Linear Trend: Similar to
the Holt method, α= 0.7 and β= 0.45 are the most
proposed coefficients.
Custom Smoothing with Exponential Trend:
Forecasting results have shown the best amount of
NCTA 2011 - International Conference on Neural Computation Theory and Applications
206

their error with α= 0.7 and β= 0.45 in this method.
Like other smoothing methods, parameters are
computed by trial and error.
Custom Smoothing with Damped Trend:
Forecasting by Damped trend is done using three
parameters: α,β and δ. The smoothing coefficients
are equal to α= 0.1,β= 0.1 and δ= 0.1. By using
these parameters the sum of square of the errors are
at a minimum.
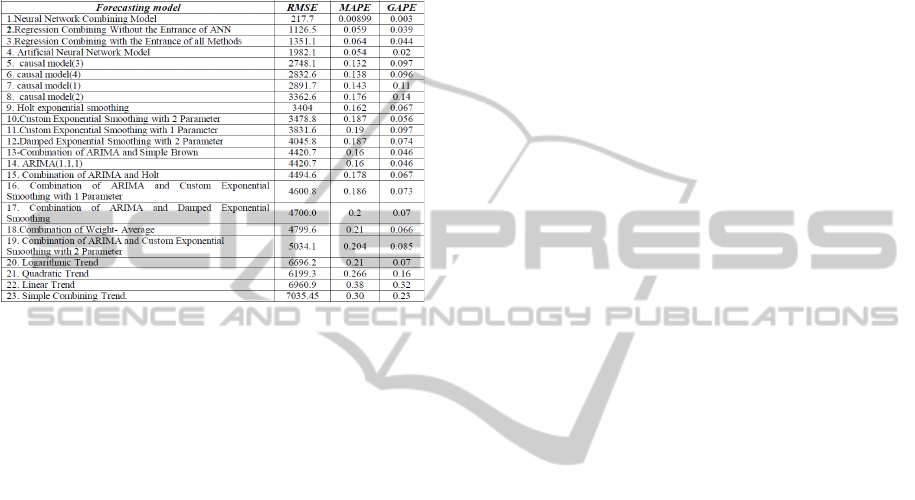
The detailed results of errors are illustrated in
Table 5.
2. Forecasting by using Trend Analysis Method:
Different trends are analyzed in trend analysis as
follow: 1.Linear Trend, 2.Logarithmic Trend,
3.Inverse Trend, 4.Quadratic Trend, 5.Cubic trend,
6.Power Trend, 7.Compound Trend, 8.S- curve
Trend, 9.Logistic Trend, 10.Growth Trend,
11.Exponential Trend
For finding the best trend, all above trends are
formulated. The best trends are selected by
considering their R2 and MSE. ANOVA (analysis of
variance) results confirm that linear trend,
logarithmic trend, quadratic trend, and compound
trend are the most suitable trends. Equations of
selected trends are listed in Table 1:
Table 1: Most suitable Trend Equations.
The detailed error results are illustrated in Table 5.
3. Forecasting by using Box- jenkins Method: In
Box- Jenkins models (ARIMA), the following
analyses for statistical modeling were carried out:
1. Determination of normality and stationary of data.
2. Using Box-Cox conversion for normalizing data and
using differentiation for stationary data.
3. Computing auto-correlation coefficients, charts, and
studying partial auto-correlation coefficients.
According to this statistical modeling [ARIMA (1, 1,
1)], parameter p equals 1, parameter q equals 1, and
parameter d equals 1. The error results of this model
and their amounts are illustrated in Table 5.
4. Econometrics Causality Methods: In these
models, the behavior of affected data is studied. The
forecasting is done by formulating the dependent
variable using the effects of independent variables.
The variables and abbreviations used in causal
modeling are shown as follow:
OP
t
= OPEC oil demand during time t.
PR
t
= Oil price during time t.
GDP= Gross Domestic Product of countries
which are OPEC oil consumers (OECD).
OE
t
= Demand for other kind-s of energy
during time t.
VAI= Added Value for industrial parts for
countries which are OPEC oil consumers.
The causal models that are obtained are illustrated in
Table 2. This Table shows the equations and also
their analysis.
In the first model, oil demand has a significant
relationship with oil price, GDP and also with other
substitution energies demand (OE). In model (2) the
relationships are logarithmic and independent
variables which have been inputted in the model are
GDP, OE and also VAE. The relationship shows the
price elasticity and also revenue elasticity with oil
demand. Model (3) is a hybrid model consisting
ARIMA and regression model. Like model (3),
model (4) is a hybrid model with combination of
MA (1). Model (5) is a long term oil demand model
with the delay demand which has been inputted in
the model. The demand’s data sets which have been
imported in the model are belonging to previous
year (one year delay). This model (5) is not
considered in combining methods, because of its
correlation within its inputted variables.
In all models p-value<=.05, Determination
coefficient R
2
and adjusted R
2
are approximately
equal to 0 .9., Durbin Watson statistics equal to 2,
and all p-values are significant for variables and
constant quantity. The error results of causal
methods are shown in Table 5.
Step 2: Forecasting Oil Demand by Neural
Networking Method: The supervised back
propagation is widely used for time series
forecasting. Therefore we decided to choose this
well-known method for forecasting OPEC oil
demand. Consequently, normalizing data, training
data and weighting the network’s inputs have been
done. Topology is selected based on continuous
changes, especially changes in the amount of the
hidden layer's neurons. The best Neural Network
Model is (5, 15,1) in which internal layer is with 15
neurons, and one output of oil demand is obtained.
Functions of middle layer are considered as sigmoid
function and transfer function is considered as linear
function. The result of errors of Neural Network
Model is shown in Table 5. The topology is similar
to combined ANN model with different numbers of
neurons and the input layers.
Step 3: Combining Individual Forecasting
Method: In this step, combining individual forecas-
DEVELOPING COMBINED FORECASTING MODELS IN OIL INDUSTRY - A Case Study in Opec Oil Demand
207
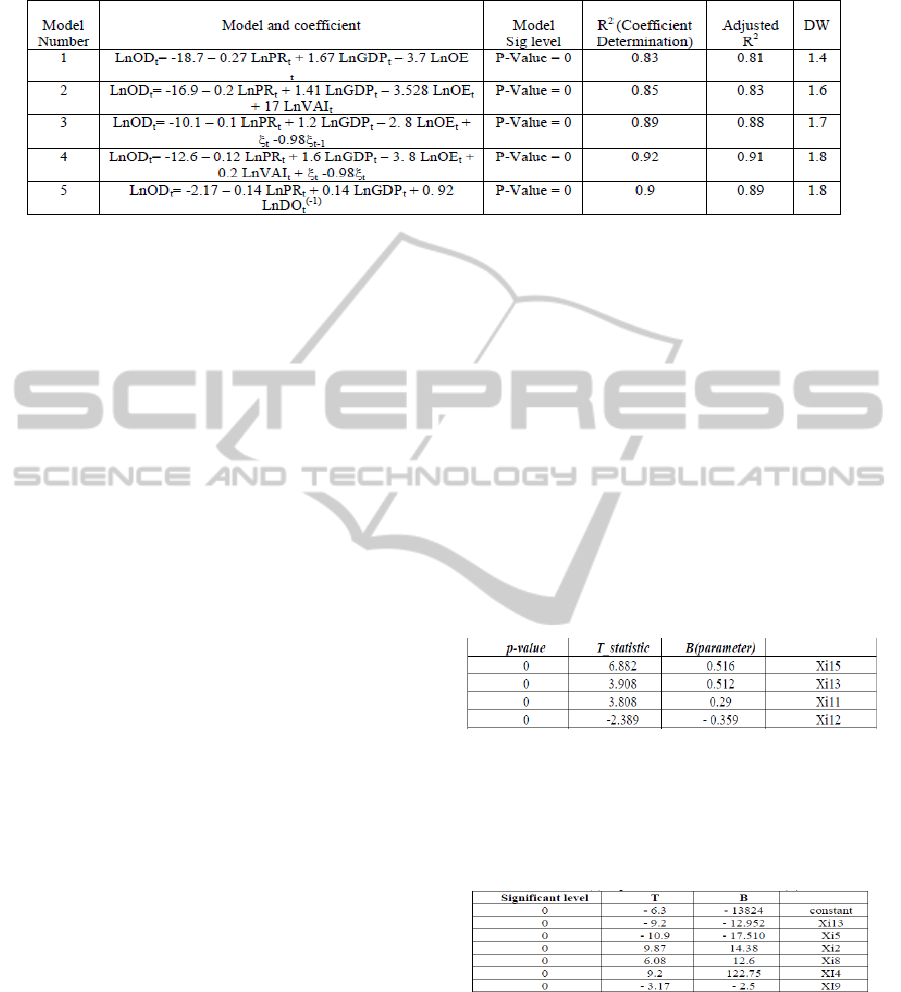
Table 2: The causal equations.
ting methods is done. Individual models which are
used in this combination are as follows:
x
i1
: Simple Brown Smoothing Methods.
x
i2
: Holt.
x
i3
: Custom Exponential Smoothing with 2
parameters.
x
i4
: Custom Exponential Smoothing with 1
parameter.
x
i5
: Damped Exponential Smoothing.
x
i6
: Linear Trend.
x
i7
: Quadratic Trend.
x
i8
: Logarithmic Trend.
x
i9
: Combining Trend.
x
i10
: ARIMA (1, 1, 1).
x
i11
: Econometric-s (First Model: independent
variables are price variables, Gross National
Product, and other energies) - Logarithmic Model .
x
i12
: Econometrics (Second Model:independent
variables are price variables, Gross National
Product, and other energies)- Logarithmic Model
plus Moving Average (MA).
x
i13
: Econometrics(Third Model).
x
i14
: Neural Network (MLP with Back Propagation).
Combining individual forecasting models is done by
using following methods:
1. Combining Individual Forecasting Methods
using Artificial Neural Network Models: We have
used supervised Multi-Layer Perceptron (MLP) back
propagation neural network in this research. In this
combination, the results of 14 individual forecasting
models (including 5 exponential smoothing models,
4 trend models, 1 ARIMA model, and 4 casual
methods) are combined. Result of each forecasting
method is considered as an input. By allocating
weights to each input, network topology is
considered with 14 inputs, 30 neurons as hidden
layer and one output layer. Transfer function used is
sigmoid function. In this model Gross Domestic
Product (GDP), oil price, consumption of other
energy resources, population and finally industrial
added- value are used as independent variables.
2. Combining Individual Forecasting Model
using Multi-variable Regression: In this
combination, the results of 14 individual forecasting
models (including 5 exponential smoothing models,
4 trend models, 1 ARIMA model, and 4 casual
methods, 1 neural network model) are combined.
Independent variables xi11, xi12, xi13… xi14 (i= 1,
2… 43) are results of individual forecasting methods
and the dependent variable is actual oil demand data
during research period (i=1,2, …, 43). The fitted
regression model use stepwise method. Fitness of
the model and the parameters are shown in Table 3.
Table 3: Significances of combined model (A).
In addition to this model, other combinations
with regression models are analyzed, and one model
without using neural network is selected. Fitness of
model and its parameters is shown in Table 4.
Table 4: Significances of combined model (B).
3. Combining with Sequential Algorithm:
Combination of smoothing method and ARIMA
method is done with sequential algorithm. The
smoothing methods results with no statistical model
can be combined with the ARIMA model with
statistical modeling. Different results of smoothing
methods have been entered in ARIMA model and
the best model is selected. Five smoothing methods
are entered into ARIMA model and fine combined
NCTA 2011 - International Conference on Neural Computation Theory and Applications
208
models are selected. ARIMA (1, 1, 1) is results of
this combination and the result of errors is shown in
Table 4. In the exponential smoothing method we
don’t have statistical modeling but the advantage of
this combination is that we can have a model.
However, n this way we cannot have considerable
reduction in the errors. This combined model is
working to telecommunication analysis, in which the
output of first model can be considered for input of
the second model.
4. Comparison of Forecasting Methods: The
comparison of forecasting methods is done based on
error indexes. In analyzing error indexes,
Armestrong et al. (1992), and Trapson (1990),
indexes been used in this research consisting RMSE,
MAPE, and GAPE.
The results of these comparisons are shown in Table
5. The comparisons are done by percentage of the
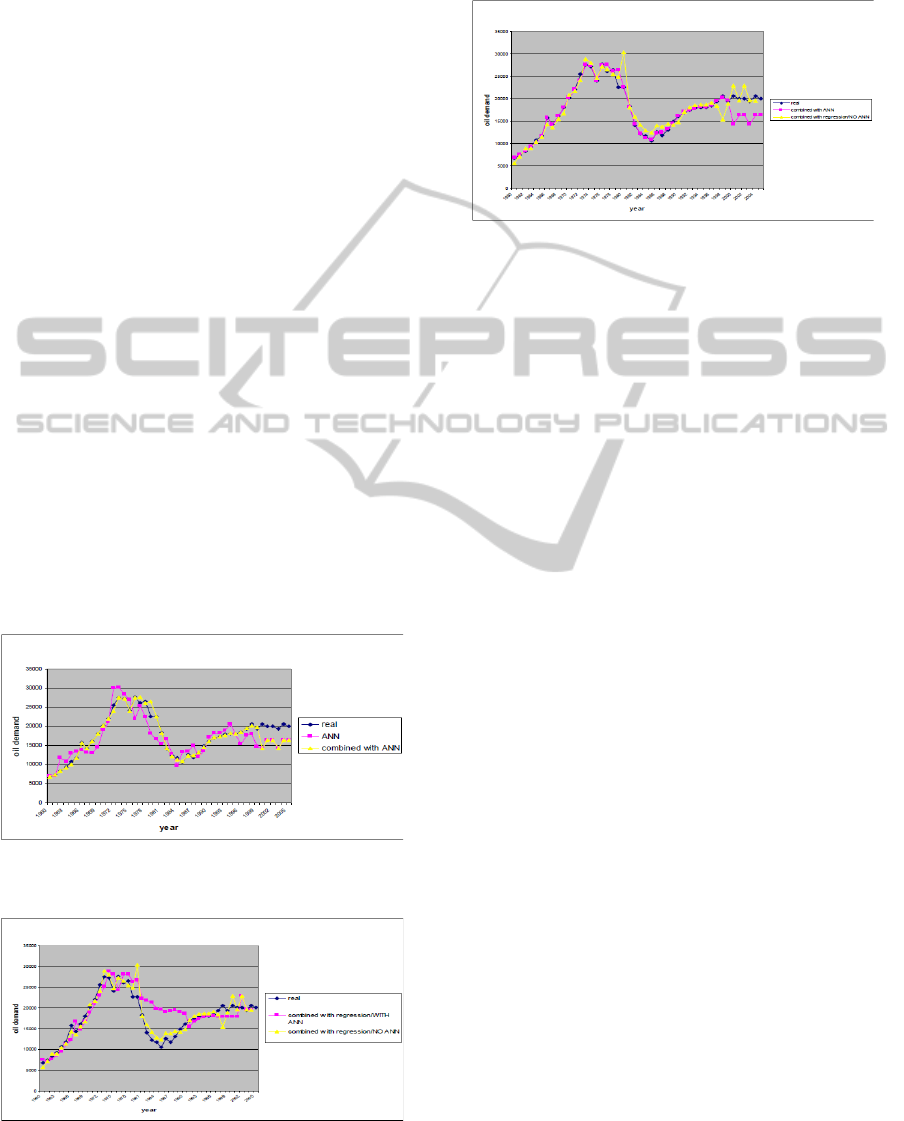
MSE. In Figures (1), (2), and (3), the comparisons of
three combined methods results, and ANN algorithm
results with real data are shown. This inter-sample
comparisons show the similarity of ANN errors with
combined ANN errors, and two other combining
methods with each other. We also have done t-test
for comparing results and the significant level (p-
value>=.05) which shows that the results doesn’t
have significant mean differences.
In this Figure, the result of combined model with
ANN and real data are compared. As we mentioned
before the mix model is done with ANN algorithm.
Figure 1: Comparison of real data with ANN/combined
ANN results.
Figure 2: Comparison of real data with two kinds of
combined regression results.
In Figure 2, the result of combined model with
regression and ANN, and the combined model with
regression without ANN are compared.
Figure 3: Comparison of real data with combined Model
method results.
As we can see in these Figures, the results of all
combination are very close, and this shows the good
performance of the combining model.
4 CONCLUSIONS AND
RECOMMENDATION
The main derived conclusions could be summarized
as follows:
1. Among different individual methods used in this
study, RMSE of ANN forecasting method provided
better results in oil demand forecasting. Oil demand
data are naturally chaotic, so because of the high
ability of artificial neural network (ANN) method in
training data and allocating suitable weights to this
data, results show the better capability of ANN for
forecasting oil demand comparing to other
individual forecasting methods.
2. Multi-variable Regression Method will do
multiple correlation tests, and therefore it omits
some of the variables in this process. But in ANN
method, all of the inputs (models) could be
considered in forecasting process. Also, based on
previous studies been reviewed in this article, ANN
method can be a useful and effective method for
combining, because in this method combining will
be done on the outputs and each of them can be
considered as absolutely independent inputs. So, if
the objective is to obtain minimum errors for
forecasting, the ANN is suggested. However, it must
be noted that ANN cannot provide the statistical
modeling.
3. Combining Exponential Smoothing with Box-
Jenkins model could not decrease the amounts of
error of each Smoothing method, and Box-Jenkins
DEVELOPING COMBINED FORECASTING MODELS IN OIL INDUSTRY - A Case Study in Opec Oil Demand
209
model separately. Based on RMSE, this combination
has an upper error level than each individual
method. However, for statistical modeling,
combination of exponential Smoothing with ARIMA
can be useful and effective.
Table 5: Models Errors Comparison and Computed Error
Standards (Original Standard is considered MSE).
4. Since in combination theories, weighted average
method is a well-known method, in present study,
this method has been used by applying weighted
based on MSE index.
In this combination analysis, weighted average has
not been like an appropriate combining method, and
its error reduction is not considerable.
The overall results of this research show
justification and feasibility of different combining
models for forecasting oil demand in OPEC, and
other energy resources suppliers. For future works,
an expert system could also be designed which can
be used to select the best method among all
combining methods.
REFERENCES
Arab Oil and Gas Directory,1985-2005.
Armstrong J. S., Collopy F., (1992). Error Measures for
generalizing about forecasting methods: Empirical
Comparison, International Journal of Forecasting 8:
69-80.
Assareh E., Behrang M. A., Assari M. R., Ghanbarzadeh
A (2010). Application of PSO (particle swarm
optimization) and GA (genetic algorithm) techniques
on demand estimation of oil in Iran. 35(12): 5223-
5229.
Bahrammirzaee A., (2010). A Comparative Survey of
Artificial Intelligence Applications in Finance:
Artificial Neural Networks, Expert System and Hybrid
Intelligent Systems, Neural Computing and
Application, 19(8): 1165-1195.
Box, G. E. P. and Pierce D. A., (1970). Distribution of
Residual Autocorrelations in Atuoreressive-Integrated
Moving Average Models. J. American Stat. Assoc. 65:
1509–1526.
Dochuchaev E. S., Rogacheva A. M., Evtushenko E. V.,
(2007). The Forecasting of the World Oil Price by
Swimming up Linear Trend and Periodic Functions;
Oil and Gas Business.
Mackay R. M., Probert S. D., (2001). Forecasting the
United Kingdom’s supplies and demands for fluid
fossil-fuels, Applied Energy 69: 161–189.
Medlock, K. B., Ronald, S. (1999), The Composition and
Growth of Energy Demand in China, China and Long-
Range Asia Energy Security: An Analysis of the
Political, Economic and Technological Factors, James
Baker III Institute for Public Policy, Rice University.
Oil Market Report, 1993-2005.
OPEC Annual Bulletin, 2000.
OPEC Oil and Energy Data, 1980-2005.
Petrov V. V., Artyushkin V. F., (2004). Prices’ Behavior
on the World Oil Market. Moscow: Fazis, P. 192.
Schrattenholzer L., (2004) Designing environmentally
compatible energy strategies: global E3 scenarios
described by IIASA models, presented at China-IEA
seminar on energy modelling and statistics, Beijing
October 20–21.
Trapson, P., (1990). An MSE statistic for comparing
forecast accuracy across series, Int. Journal of
forecasting 6: 219-227.
Zhang, G., Pattuwo, E. B., Hu, M. Y., (2001). A
simulation Study of Artificial Neural Networks for
Nonlinear Time Series Forecasting, Computers &
Operation Research, 28:381-396.
NCTA 2011 - International Conference on Neural Computation Theory and Applications
210
