FUZZY CONNECTEDNESS IN SEGMENTATION OF

MEDICAL IMAGES

A Look at the Pros and Cons

Pawel Badura, Jacek Kawa, Joanna Czajkowska, Marcin Rudzki and Ewa Pietka

Institute of Electronics, Silesian University of Technology, Akademicka 2A, 44-100 Gliwice, Poland

Keywords:

Fuzzy connectedness, Medical image segmentation.

Abstract:

An attempt to recapitulate and conclude numerous experiences with the fuzzy connectedness theory applied

to medical image segmentation is made in this paper. The fuzzy connectedness principles introduced in 1996

have been developed and tested in dozens of studies in past 15 years; many advantages, as well as shortcomings

have been discovered and described. Some aspects of the method and its applications have been summarized

here, including the examples of speciﬁc 2D and 3D medical studies with various objects, subjected to fuzzy

connected segmentation. Deliberation about the usefulness of multiseeded and multiobject variants is also

present. An algorithm optimized for matrix computations-based programming languages is introduced. Fi-

nally, 3 fuzzy connectedness-based computer aided diagnosis systems are described and evaluated.

1 INTRODUCTION

There are plenty of areas in the wide world of fuzzy

computations. One of them is the fuzzy connected-

ness (FC) theory, taking advantage of basics of fuzzy

logic, sets and relations. Deﬁned as a methodology

operating on multidimensional and multifeature sets

of ordered and connected data, FC is suited for im-

age processing, in particular for image segmentation.

Segmentation is a process of partitioning an image

into multiple, separate objects – sets of image points,

like pixels or voxels, depending on image dimension-

ality. The points classiﬁed into single objects are

strongly connected to each other by some more or less

abstract relations, whilst their relations to points con-

stituting other objects have relatively lower values. If

the features associated with the points are multival-

ued (e.g. grayscale images, like in most medical im-

ages and volumes, taken from Computed Tomogra-

phy CT, Magnetic Resonance MR or Ultrasonography

USG studies), then the fuzzy computations seem to be

perfect in an advanced analysis. For this reason im-

age processing researchers in past decades willingly

introduced some fuzziness into their job.

The point of view that can be taken on such a topic

is twofold: (1) FC method applied to a speciﬁc task of

image segmentation or (2) image segmentation per-

formed by a speciﬁc tool – FC. Anyway, this paper

comprises a broad look at the fuzzy connectedness in

the segmentation of medical images. After a short re-

view of FC fundamentals, an analysis of character-

istic segmentation subjects is performed, with some

notes on FC variants. Then, the dimensionality and

computational complexity is taken into consideration.

An algorithm optimized for Matlab

applications is

proposed. Finally, after a brief presentation of 3 com-

puter aided diagnosis (CAD) systems along with re-

sults obtained at the evaluation stage, some conclu-

sions are made.

2 FUZZY CONNECTEDNESS

The idea of fuzzy connectedness relies on performing

soft computations in digital spaces. The basic work

(Udupa and Samarasekera, 1996) provides deﬁnitions

of multiple fuzzy relations within topologically or-

dered dataset C, in particular the fuzzy afﬁnity κ:

κ = {((c, d), µ

(c, d)) | c, d ∈ C×C}, (1)

where µ

∈ [0, 1] is the fuzzy afﬁnity membership

function, and c, d are spels (spatial elements) in C.

If C is a set of image points, then c and d might be

treated as pixels or voxels. The value of µ

is based

on the c and d features, like coordinate adjacency,im-

age intensities I(c), I(d) or local intensity gradients.

Fuzzy afﬁnity has to be reﬂexive: µ

(c, c) = 1 and

486

Badura P., Kawa J., Czajkowska J., Rudzki M. and Pietka E..

FUZZY CONNECTEDNESS IN SEGMENTATION OF MEDICAL IMAGES - A Look at the Pros and Cons.

DOI: 10.5220/0003670904860492

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FCTA-2011), pages 486-492

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

symmetric: µ

(c, d) = µ

(d, c) for all c, d ∈ C. It is

mostly used in the form of:

(c, d) = µ

(c, d) · g(µ

(c, d), µ

(c, d)) (2)

with µ

being the functional form of adjacency rela-

tion α (e.g. hard 6-neighbourhoodin a 3D or 4-neigh-

bourhood in a 2D image) and µ

, µ

– the intensity-

based, and intensity gradient-based parts of the afﬁn-

ity, respectively. Several forms of (2) have been illus-

trated and discussed in (Saha et al., 2000). Most of

the studies prefer the weighted gaussian variant:

(c, d) = µ

(c, d)









I(c)+I(d)

−m



2σ

(

|I(c)−I(d)|−m

)

2σ





. (3)

, σ

, m

, σ

are parameters of κ related to the inten-

sities of segmented object; they are often computed

based on the features of seed points and their neigh-

bours. Weights w

, w

balance the inﬂuence of µ

, µ

both being positive and w

+ w

= 1.

Adjacency relation α causes µ

to be nonzero

only for pairs of neighbouring spels c and d. Such

a pair is called a link, and the value of µ

(c, d) –

its strength. Consequently, a path is any sequence

of spels he

, e

, ..., e

i such that for any i ∈ [1, m− 1]

a pair he

, e

i+1

i is a link. It is noted p

if c = e

and d = e

. The strength of a path is a strength of

its weakest link – the smallest afﬁnity along the path:

) = min

{µ

, e

i+1

)} (4)

Finally, any image spels c and d are fuzzy connec-

ted according to relation K. The membership function

of fuzzy connectedness µ

(c, d) is the strength of the

strongest path p

of all the paths between c and d,

forming a set P

(c, d) = max

∈P

[µ

)] (5)

FC-based segmentation requires the selection of

seed point o inside an object, and then computation

of fuzzy connectivity scene C

for all spels c ∈ C:

(o, c), (6)

with the unitary connectivity of a seed point:

(o) = µ

(o, o) = 1. The Dijkstra’s Algorithm (Car-

valho et al., 1999) has been proposed to solve such

a speciﬁc shortest path problem faster than with the

dynamic programming approach (Udupa and Sama-

rasekera, 1996). It is also valid in case of all multi-

seeded applications (Saha and Udupa, 2001), where

set O of M (M > 1) seed points o

is indicated, as well

as in the relative fuzzy connectedness (RFC) methods

(Herman and Carvalho, 2001), (Udupa et al., 2002),

(Ciesielski et al., 2007), (Badura and Pietka, 2007), to

be discussed later in the paper. Nevertheless, if there

is indeed more than a single seed point for the object,

the scene C

for a set O is a fuzzy union:

[

∈O

[µ

, c)]. (7)

The ﬁnal determination of segmented object might

be done by the binarisation of sceneC

with threshold

θ ∈ [0, 1], resulting in binary image O

κθ(o)



1 ⇔ C

0 otherwise.

(8)

The RFC variant uses the second object, treated as

a background region with its own seed point b, to de-

termine O

κθ(o)

in a rivalry mode. Spel c ∈ C belongs

to an object according to afﬁnity κ and connectedness

K if µ

(o, c) > µ

(b, c). The above condition leads

to fuzzy connectivity scenes C

and C

and their com-

parison in a form of a ”division of spoils”.

The list of medical image processing applications,

where the FC method has been used is already long,

yet still far from completion. Let us notice here

just a few segmentation applications: airway trees

(Tschirren et al., 2005), multiple sclerosis (Udupa

et al., 1997), (Admasu et al., 2003), (Kawa and Pietka,

2008), brain cancer (Moonis et al., 2002), lung cancer

(Badura and Pietka, 2008), (Dehmeshki et al., 2008),

bone cancer (Czajkowska et al., 2010), angiography

(Abrahams et al., 2002), colonoscopy (Udupa et al.,

2001). In many cases FC is treated as a part of a wider

methodology, mostly used for ﬁne segmentation. The

authors of this paper have adapted various models of

FC into segmentation of a variety of anatomical struc-

tures. Some examples and an analysis presented in the

following sections are an attempt to point out areas,

where FC provides an effective outcome, mentioning

also applications requiring modiﬁcations.

3 SUBJECT ANALYSIS

3.1 Solid & Well Circumscribed Tissues

If an anatomical structure to be delineated features

an intensity distinctly different than the surrounding

regions, most of the well known segmentation meth-

ods may show their best. The above rule refers both

to: the edge detection (because the edges are sharp

enough), and the region-based methods. The FC ap-

proach belongs to the latter, as a particular type of

FUZZY CONNECTEDNESS IN SEGMENTATION OF MEDICAL IMAGES - A Look at the Pros and Cons

487

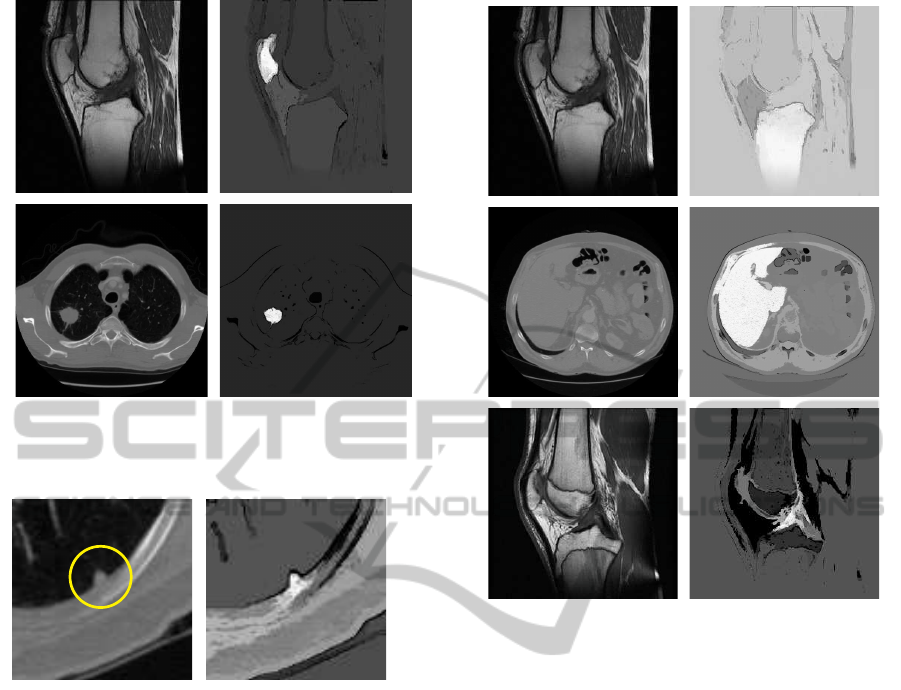
(a)

(b)

Figure 1: Typical well circumscribed objects (left) and their

FC scenes (right). Objects (M – number of seed points):

patella in MR, M = 1 (a), lung nodule in CT, M = 1 (b).

Figure 2: ROI within a thoracic CT with the juxtapleural

lung nodule (left) and its FC scene (right).

a region growing algorithm. In cases of clearly vis-

ible tissues without signiﬁcant level of noise (or de-

noised by some sort of preﬁltering) the canonic form

of FC usually yields very good results. The selection

of threshold θ is quite simple, due to the histogram

bimodality of fuzzy connectivity scene C

. Moreover,

such approaches are practically insensitive to the lo-

cation of a seed point, if only located inside an object.

The fuzzy connectivity scenes of a couple of typical

structures are illustrated in Figure 1.

As in all the region growing applications there is

a danger of a ”leak” if there are any ”bridges” be-

tween the object and a region with similar intensity.

Such a problem is visible in case of pleura-connected

lung nodules, where the employment of some prepro-

cessing methods is indispensable (Figure 2).

3.2 Soft Tissues

The fuzziness brought in by the method seems to be

more interesting in difﬁcult cases. Already (Udupa

and Samarasekera, 1996) point out the FC’s good per-

(a)

(c)

(b)

Figure 3: Typical objects more difﬁcult to delineate (left)

and their FC scenes (right): tibia in MR, M = 2 (a), liver in

CT, M = 1 (b), anterior cruciate ligament in MR, M = 2 (c).

formance in the presence of object-independent ”in-

tensity ramps”, mainly due to an enhancement pro-

vided by the gradient-based afﬁnity component µ

(Figure 3a). Another, yet more frequent example is

a segmentation of regions with slight intensity dif-

ferences, which corresponds to e.g. the abdominal

structures in the CT studies (Figure 3b).

In all cases mentioned above it is advisable to ob-

tain a larger number of seed points, since it leads to

more reliable values of afﬁnity parameters m and σ.

Besides, the computations (growth) of a fuzzy con-

nectivity scene start from many points. If the process-

ing stages preceding the FC analysis are trustworthy

enough, they might even produce full binary masks

corresponding to the core of an object, passed as sets

of seed points to the FC.

Because of the blurred edges between the struc-

tures and therefore less evident slopes in the fuzzy

connectivity scene, the relative FC modes are always

recommended here, despite their greater time con-

sumption. Figure 3c shows the anterior cruciate liga-

ment in a MR slice well separated from the bone, fat

and muscle regions, yet hardly distinguishable from

articular capsule ﬂuids and tissues. Treating the lat-

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

488

Figure 4: ROI within a thoracic CT with the low intensity

lung nodule (left) and its FC scene (right).

ter as a background region with its own seed points

and fuzzy connectivity scene and giving permission

for a ”battle for pixels” usually increases the method

performance.

3.3 Homogeneous vs Inhomogeneous

Regions

Homogeneity of a segmentation subject is a separate

issue, although it refers mainly to the previous sec-

tion. The noise present in the images brings more

problems within the regions, where the intensities

of adjacent structures differ slightly. In the FC ap-

proaches it might lead to leaks or more or less sig-

niﬁcant ”holes” within the fuzzy connectivity scene

region corresponding to an object. Note the liver in

Figure 3b: the inhomogeneity is even more appar-

ent in the fuzzy connectivity scene than in the orig-

inal slice. The image data for the FC analysis should

be prepared, e.g. by the anisotropic diffusion (Per-

ona and Malik, 1990), and additionally postprocessed

e.g. using the mathematical morphology (Gonzalez

and Woods, 2002).

An even more clear example is illustrated in Fig-

ure 4, including an inhomogeneous, vascular lung

nodule with very low intensity. The vessel is sepa-

rated well enough; the lung parenchyma, however, is

not. Thresholding the scene could make binary object

κθ(o)

torn or expanded. It is a perfect case to em-

ploy the RFC with a seed point somewhere within the

parenchyma and determine the boundary between the

object and the background by comparing two scenes.

Compare this boundary-setting mechanism to the wa-

tershed algorithm (Gonzalez and Woods, 2002).

3.4 Multiseeded and Multiobject

Approaches

As mentioned above, the performance of FC algo-

rithms improves with an increasing number of seed

points (as in each seeded segmentation method). Usu-

ally, the seed points indicate the core of an object.

With many seed points, the mean distance from the

Figure 5: ROI within an abdominal MR slice with the Ew-

ing’s sarcoma (left) and its FC scene (right).

seed to the object boundaries shorten, which avoids

a potential undersegmentation mechanism. On the

other hand, the determination of fuzzy afﬁnity func-

tion parameters (m, σ in (3)), often relies on the fea-

tures of seed points and their neighbours. In case of

a multiseeded approach such a way of computations

makes the parameters better representatives of an ob-

ject, due to averaging phenomenons. However, the

parameters can be estimated using clustering methods

(e.g. Fuzzy c-Means or Gaussian Mixture Models).

The manual indication of multiple seed points

is rarely performed, because the segmentation ap-

proaches should rather be as automatised as possi-

ble. However, ”indication” might be understood as

”getting as a result of some preprocessing opera-

tion”, which actually allows full automatisation. Sev-

eral such solutions have been designed in our re-

search, e.g. automatic selection of multiple seed

points spread within an object via an evolutionary

algorithm (Badura and Pietka, 2007) or passing the

presegmentation-made binary masks as sets of seed

points (Kawa and Pietka, 2008), (Czajkowska et al.,

2010). The exemplary fuzzy connectivity scene re-

sulting from the latter is presented in Figure 5, where

the object region (a Ewing’ssarcoma) is mostly white,

which relates to the connectivity level at 1.0.

If many adjacent objects have to be determined,

the multiobject FC (Herman and Carvalho, 2001)

might be employed, with at least one seed per each of

the M objects. After getting the M fuzzy connectiv-

ity scenes a defuzzifying decision is made, about the

membership of each point: it is attached to the object

with the strongest connectivity value. In particular, if

two objects are taken into consideration, the method is

called relative fuzzy connectedness. At least one seed

is sown in the object, and at least one – in the back-

ground. In our research this mode has been used a lot

of times, many of them involving object-multiseeded

approaches, as described above.

FUZZY CONNECTEDNESS IN SEGMENTATION OF MEDICAL IMAGES - A Look at the Pros and Cons

489

Figure 6: ROI within preﬁltered abdominal CT volume with

liver vasculature (left) and corresponding FC scene (right).

3.5 Dimensionality Analysis

The challenge presented by the FC in the image do-

main is connected with the digital space dimensional-

ity. In the 3D analysis, a number of possible paths is

much higher than in the 2D space and analysis time

increases. In our works both, 2D and 3D modes of

the FC have been performed in multiple, indepen-

dent researches. Depending on the segmentation sub-

ject, various hard adjacency relations α have been em-

ployed: 4- or 8-neighbourhood in 2D as well as 6-,

18- and 26-neighbourhood in 3D. The rule is clear in

all the dimensions: the smaller (closer) the neighbour-

hood for fuzzy afﬁnity κ is: (1) the lower the mean

value of fuzzy connectivity scene is, (2) the lower

the possibility of a ”leak” occurrence is, (3) the faster

the computations are. You may ﬁnd any of these fea-

tures more important than the other. We mostly prefer

smaller neighbourhoods, since they produce good re-

sults in reasonable time.

A similar remark does not have to be made refer-

ring to the µ

form. It practically does not depend on

the image dimensionality, since equations (1)-(8) take

into consideration two points, independently of how

many coordinates they have. So, we did not make any

particular distinction between 2D and 3D µ

-s.

The practical application in a 3D space may also

be complicated by the inhomogeneous dimensions of

a voxel (a cuboid instead of a cube). Mainly, an in-

terpolation is to be performed in the Z-direction to

ensure the FC not to discriminate any axis. However,

we tried to analyse the FC within uninterpolated vol-

umes, achieving proper segmentation results.

A few consecutive slices of the fuzzy connectivity

scene for a 3D segmentation of liver vasculature are

presented in Figure 6.

Due to the increased computation time, testing

various FC-based methods in the 3D medical images

is harder than in 2D. A robust and fast implemen-

tation is necessary that could be easily deployed in

various image segmentation tasks and integrated with

our prototyping environment (currently Matlab). In

the following section an algorithm optimized for such

conditions is presented.

4 MATLAB OPTIMIZED FC

ALGORITHM

In Matlab the standard FC method (Udupa and Sama-

rasekera, 1996), as well as the Dijkstra’s search

algorithm-based version (Carvalho et al., 1999) can

both be implemented. Both these approaches are far

from optimal for direct use in Matlab, as they operate

iteratively on the separate image points.

Matlab is a weakly-typed, interpreted language

optimized for the matrix computation. In Matlab,

an algorithm implemented by means of standard for

loops and indexing can be much slower than the same

algorithm implemented by operations on the whole

matrices. The process of optimization, that replaces

slow element-wise operations by fast matrix-based

ones is in Matlab known as vectorization.

As images are represented as 3D matrices (tables)

with a basic type of ﬂoating point or integer num-

ber, the vectorized implementation can signiﬁcantly

speed processing. The algorithm presented below

uses the basic 3D manipulation functions available:

circshift

padarray

and the matrix-wise

min/max

operations. It can process any number of seed points

in parallel, providing all of them has been chosen

within a single processed object. Using the precom-

puted afﬁnity tables (step 4), the operations are sped

up, but if the memory is a critical factor, the afﬁnity

tables can also be recomputed in each iteration.

1. Chose the hard adjacency relation α.

2. Decompose α to the series of shifts s denoting

neighbouring elements (e.g. a 2D 4-connectivity

consists of: (1) one to the left, (2) one to the right,

(3) one to the bottom and (4) one to the top).

3. Preprocess the original image by padding rows,

columns and layers as not to permit for wrapping

the original values in the later steps.

4. Precompute the fuzzy afﬁnity values for each

neighbourhood member (one table T

containing

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

490

the afﬁnity values for each α-connected member;

e.g. 4 tables if 4-connectivity has been chosen;

e.g. T

for the one to the left).

5. By using circular shift of the precomputed fuzzy

afﬁnity tables ensure, that the element of a new

respect to the s-th neighbour; e.g. for a pixel c =

, c

) T

, c

) contains µ

(c, d) with respect to

the left pixel d = (c

− 1, c

6. Prepare zeroed matrix C

and set all the elements

matching the seed point locations to ones.

repeat

for each Ts

TEMP = min(Co, Ts);

Co = max(Co, TEMP);

end

while Co changes

where

min

and

max

are the element-wise matrix

operations.

This can be further sped up if the FC is to be used

in the segmentation by thresholding. Each T

ma-

trix can be thresholded and

min/max

can be replaced

by the logical

and/or

operations, respectively. Our

experiences show that the proposed implementation

shortens the computation time compared to the clas-

sic Dijkstra search algorithm by a few times.

5 RESULTS

As mentioned above, in most applications the FC

analysis is used as a part of a wider methodology. It is,

however, usually the critical part of the segmentation

step. It is also the case in our research. Let us point

out 3 of our CAD applications with a brief description

and a results summary.

5.1 Multiple Sclerosis CAD

A 2D relative FC has been used in a Multiple Scle-

rosis (MS) CAD system (Kawa and Pietka, 2008).

The FC is used in the second step of segmentation

in the MR FLAIR images (when location of plaques

has already been established). The MS plaques are

visible in the MR as small, conﬂuent lesions. Due

to a low spatial resolution and small differences in

a signal level, it is not always clear, also to the ra-

diologists, where a boundary of a separate lesion is

located. Using the FC permits to set the continuous

zero for elements, that have not been reached yet, tested

path strength otherwise.

update, if tested path strength is best so far.

border between a normal and affected tissue. The FC

analysis is initiated in regions surrounding previously

segmented lesions, with a standard afﬁnity and auto-

matically estimated parameters. The results are veri-

ﬁed using gold standard images obtained by the expe-

rienced radiologist. The mean sensitivity for various

test sets varies from 83% to 91%.

5.2 Lung Nodule CAD

A 3D FC in a modiﬁed relative mode stands for

a main segmentation stage (Badura and Pietka, 2007),

(Badura and Pietka, 2008). It is preceded by the

presegmentation (including the manual selection of

two seed points, determination of the primary bi-

nary masks for the objects and automatic selection

of the sets of seed points) and followed by post-

processing stage (the vessel removal and correction

procedures). The Lung Image Database Consortium

(LIDC) database, containing 23 cases of various pul-

monary nodules, has been used for evaluation (note

Figures 1b, 2 and 4). The CT studies have been de-

scribed by the voxel probability maps, obtained in the

multistage delineation process, involving experienced

radiologists. At the evaluation stage all cases have

been segmented with the various pairs of manually in-

dicated seed points. The mean sensitivities obtained

in the study were 99.94% for the voxels, whose values

in the probability map were equal to 1.0 and 90.94%,

when their values exceeded 0.5. The mean false posi-

tive rate was 0.39%.

5.3 Bone Cancer CAD

A 3D relative FC on the basis of a gaussian mix-

ture model has been used in the Bone Cancer CAD

(Czajkowska et al., 2010). The database consists of

71 examinations of 48 patients with various types of

bone lesions (tumour and tumour-like),grouped into 8

classes, i.a. Osteosarcomas, Ewing’s sarcomas (Fig-

ure 5) and Chondrosarcomas. A total of 118 differ-

ent MR series have been analysed (T1 contrast en-

hanced, T2 with fat saturation, STIR and PD). The

evaluation stage consists of two parts: the model-

based and the radiologist opinion-based veriﬁcation.

The model-based step has been performed on the ba-

sis of 24 series. The models have been prepared using

segmentation results veriﬁed by the radiologist in or-

der to create additional, synthetic volumes. The mean

sensitivity yielded using the model-based evaluation

was 96.05% with speciﬁcity at 98.74%. The second

veriﬁcation step has been performed based on the ra-

diologist opinion. Here, the algorithm worked cor-

rectly in 74.5% of 118 cases.

FUZZY CONNECTEDNESS IN SEGMENTATION OF MEDICAL IMAGES - A Look at the Pros and Cons

491

6 CONCLUSIONS

In the computer aided diagnosis, the image seg-

mentation is often used as a ﬁrst step in an au-

tomated case analysis. As such, it beneﬁts from

the fuzzy notion provided by the fuzzy connected-

ness. After 15 years since being announced the fuzzy

connectedness-based algorithms appeared in multiple

segmentation applications and programming environ-

ments (e.g. note the speciﬁed FC ﬁlters in the ITK –

Insight Toolkit – environment). The properly deﬁned

connectedness between points within objects is help-

ful in achieving precise and reliable delineation of the

structures. Sometimes the FC analysis is sufﬁcient as

a standalone segmentation method; other times it pro-

vides just the most accurate part of a larger process.

The spatial relations and fuzziness used in the seg-

mentation step permit better resemblance to the pro-

cessing performed by the human brain and perceptual

system. In our work the fuzzy connectedness proved

to be a powerfull tool; we can conclude, that its fuzzi-

ness improves ﬂexibility of the segmentation process.

REFERENCES

Abrahams, J. M., Saha, P. K., Hurst, R. W., LeRoux,

P. D., and Udupa, J. K. (2002). Three-Dimensional

Bone-Free Rendering of the Cerebral Circulation Us-

ing Computed Tomographic Angiography and Fuzzy

Connectedness. Neurosurgery, 51:264–269.

Admasu, F., Al-Zubi, S., Toennies, K., Bodammer, N., and

Hinrichs, H. (2003). Segmentation of Multiple Scle-

rosis Lesions from MR Brain Images Using the Prin-

ciples of Fuzzy-Connectedness and Artiﬁcial Neuron

Networks. In International Conference on Image Pro-

cessing, ICIP 2003, volume 2, pages II 1081–1084.

Badura, P. and Pietka, E. (2007). Semi-Automatic Seed

Points Selection in Fuzzy Connectedness Approach

to Image Segmentation. In Computer Recognition

Systems 2 (Advances in Soft Computing), volume 45,

pages 679–686. Springer-Verlag.

Badura, P. and Pietka, E. (2008). Pre- and Postprocessing

Stages in Fuzzy Connectedness-Based Lung Nodule

CAD. In Information Technologies in Biomedicine

(Advances in Soft Computing), volume 47, pages 192–

199. Springer-Verlag.

Carvalho, B. M., Joe Gau, C., Herman, G. T., and

Yung Kong, T. (1999). Algorithms for Fuzzy Seg-

mentation. Pattern Analysis & Applications, 2:73–81.

Ciesielski, K. C., Udupa, J. K., Saha, P. K., and Zhuge, Y.

(2007). Iterative Relative Fuzzy Connectedness for

Multiple Objects with Multiple Seeds. Comput. Vis.

Image Underst., 107(3):160–182.

Czajkowska, J., Badura, P., and Pietka, E. (2010). 4D Seg-

mentation of Ewing’s Sarcoma in MR Images. In

Information Technologies in Biomedicine: Volume 2

(Advances in Intelligent and Soft Computing), vol-

ume 69, pages 91–100. Springer-Verlag.

Dehmeshki, J., Amin, H., Valdivieso, M., and Ye, X.

(2008). Segmentation of Pulmonary Nodules in Tho-

racic CT Scans: A Region Growing Approach. IEEE

Transactions on Medical Imaging, 27(4):467–480.

Gonzalez, R. and Woods, R. (2002). Digital Image Process-

ing. Prentice Hall, Upper Saddle River, NJ.

Herman, G. T. and Carvalho, B. M. (2001). Multiseeded

Segmentation Using Fuzzy Connectedness. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 23(5):460–474.

Kawa, J. and Pietka, E. (2008). Automated Fuzzy-

Connectedness-Based Segmentation in Extraction of

Multiple Sclerosis Lesions. In Information Technolo-

gies in Biomedicine (Advances in Soft Computing),

volume 47, pages 149–156. Springer-Verlag.

Moonis, G., Liu, J., Udupa, J. K., and Hackney, D. (2002).

Estimation of Tumor Volume Using Fuzzy Connect-

edness Segmentation of MRI. Am. J. Neuroradiol.,

23(3):356–363.

Perona, P. and Malik, J. (1990). Scale-Space and Edge De-

tection Using Anisotropic Diffusion. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

12(7):629–639.

Saha, P. K. and Udupa, J. K. (2001). Fuzzy Connected Ob-

ject Delineation: Axiomatic Path Strength Deﬁnition

and the Case of Multiple Seeds. Computer Vision and

Image Understanding, 83(3):275–295.

Saha, P. K., Udupa, J. K., and Odhner, D. (2000). Scale-

Based Fuzzy Connected Image Segmentation: The-

ory, Algorithms, and Validation. Computer Vision and

Image Understanding, 77(9):145–174.

Tschirren, J., Hoffman, E. A., McLennan, G., and Sonka,

M. (2005). Intrathoracic Airway Trees: Segmentation

and Airway Morphology Analysis from Low-Dose

CT Scans. IEEE Transactions on Medical Imaging,

24(12):1529–1539.

Udupa, J. K., Odhner, D., and Eisenberg, H. C. (2001).

New Automatic Mode of Visualizing the Colon via

CT. In SPIE: Medical Imaging, volume 4319, pages

237–243, San Diego, CA.

Udupa, J. K., Saha, P., and Lotufo, R. (2002). Relative

Fuzzy Connectedness and Object Deﬁnition: Theory,

Algorithms, and Applications in Image Segmentation.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 24(11):1485–1500.

Udupa, J. K. and Samarasekera, S. (1996). Fuzzy Connect-

edness and Object Deﬁnition: Theory, Algorithms,

and Applications in Image Segmentation. Graphical

Models and Image Processing, 58(3):246–261.

Udupa, J. K., Wei, L., Samarasekera, S., Miki, Y., van

Buchem, M. A., and Grossman, R. I. (1997). Mul-

tiple Sclerosis Lesion Quantiﬁcation Using Fuzzy-

Connectedness Principles. IEEE Transactions on

Medical Imaging, 16(5):598–609.

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

492