
ANALYSIS OF MAPPING WITHIN S-MODULE FRAMEWORK
Krzysztof Goczyla, Aleksander Waloszek, Wojciech Waloszek and Teresa Zawadzka
Dept. of Software Engineering, Gdansk University of Technology, Narutowicza 11/12, Gdansk, Poland
Keywords: Ontology, Ontology modularization, Description logics, Ontology mapping, Ontology importing.
Abstract: In this paper we present the results of our work on s-module (semantic modules) framework. The
framework, introduced recently, consists of a high-level semantic description of a modular knowledge base
accompanied by an algebra for manipulating module contents. The main contribution of the article is the
presentation of the process of expressing Distributed Description Logics knowledge base within the
s-module framework. As the two methods exhibit two different approaches to modularization, analysis of
this procedure is helpful in capturing the specifics of DDL, comparing it to other methods, and discussing
the completeness of the s-module framework.
1 INTRODUCTION
Recently significant amount of effort has been put in
the area of on ontology modularization. Ontologies
gain importance in Computer Science, and use of
modularization techniques broadens the possibilities
of their efficient development and deployment.
In this paper we continue our work from
(Goczyla et al., 2009a) on analyzing spaces of
semantic modules (s-modules). In (Goczyla et al.,
2009a) we described a procedure for constructing a
space of possibly useful modules. Construction of
the space is algebraic: we specify a set of base
modules and a set of operators. Therefore,
assimilation of knowledge by one module from
another can be depicted as a “shift” in this space and
described as a sequence of algebraic operations.
The s-module space was introduced as a
common framework for describing properties and
characteristics of a modular knowledge base or a
specific modularization approach. In this paper we
present a procedure of expressing Distributed
Description Logics (DDL; Borgida and Serafini,
2003) knowledge base in this space. The conclusions
are rather encouraging: such a translation is possible
with a minimal number of additional assumptions
and with choose of very natural base modules. The
description is a source of interesting observations
about DDL and s-module space, moreover, it
provides an alternative way of proving soundness
and completeness of the method.
2 PRELIMINARIES
Due to space limitations we cannot present the full
introduction to ontologies formulated in Description
Logic (DL) ALC. Here we only review basic terms
to establish the notation used henceforth.
In all DLs we assume that we have three sets of
names: constants (individual names), concepts
(unary predicates), and roles (binary predicates).
The full signature
contains all the valid names.
Other signatures S are subsets of
.
The names are interpreted, and each interpre-
tation I = (Δ
I
, ·
I
) consists of a non-empty domain
Δ
I
and an interpretation function ·
I
which assigns
each constant an element of Δ
I
, each concept a
subset of Δ
I
, and each role a subset of Δ
I
ä Δ
I
. We
assume that every base interpretation I of every in
fact interprets all the valid names from
.
Projection I|S of a base interpretation to some
selected signature S produces a set of interpretations
with the same domain as I and interpreting all the
names from S in the same way:
I|S = {J: Δ
J
= Δ
I
∀X ∈ S: X
J
= X
I
} (1)
An ontology O is simply a set of sentences. A
signature of O, denoted Sig(O), is the set of all
names used in any sentence of O. An interpretation
I satisfies O (is its model; denoted I O) iff it
satisfies all the sentences in O. Naturally if I O
then every J ∈ I|Sig(O) also satisfies O.
267
Goczyla K., Waloszek A., Waloszek W. and Zawadzka T..
ANALYSIS OF MAPPING WITHIN S-MODULE FRAMEWORK.
DOI: 10.5220/0003665402670272
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2011), pages 267-272
ISBN: 978-989-8425-80-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

3 S-MODULE SPACE
In this section we describe s-module approach
introduced in (Goczyla et al., 2009a). The semantic
modules are defined in a way which disregards the
exact form of a language (like DL) and focuses only
on interpretations. Each semantic module is in fact a
set (more precisely, a class) of base interpretations.
Each semantic module also has a finite signature S
which expresses the range of names about which we
want to reason using the module:
Definition 1. A s-module M = (S, W) is a pair of a
signature S and a class W of base interpretations,
such that W|S = W. Each interpretation from W is
called a model of M.
Henceforth we use S(M) and W(M) to describe
the two parts of a s-module M.
For any ontology O we might construct a module
M(O) such that W(M(O)) = {I: I O} and
S(M(O)) = Sig(O). However, while M(O) holds all
the possible (base) models of the ontology O, it
“forgets” the exact form of sentences; e.g.
M({A B}) = M({A
≡ A B}).
(Goczyla et al., 2009a) define a number of ope-
rations for s-modules (M, L denote arbitrary s-mo-
dules, S any signature, γ a function
ö
):
M L = (S(M) S(L), W(M) W(L)) (2)
M L = (S(M) S(L), W(M) W(L))
(3)
M ‒ L = (S(M) S(L), W(M) ‒ W(L))
(4)
ρ
γ
(M) = (γ(S(M)), γ(W(M)))
(5)
π
S
(M) = (S, W(M)|S)
(6)
The operations , ρ, π form the backbone of the s-
module algebra. The intersection () of s-modules
representing ontologies corresponds to adding all
sentences (importing) from one ontology to another:
M(O
1
) M(O
2
) = M(O
1
O
2
).
Simple importing is possible only if there is no
name conflict between two ontologies. In the
presence of name conflicts we can use the rename
operator (ρ). Rename operation (ρ) uses the notion
of a signature mapping, which is a function γ:
ö
. We also (like in (5)) apply γ to an
interpretation in which case γ(I) = J such that
Δ
I
= Δ
J
and ∀X ∈
: γ(X)
J
= X
I
.
Sometimes we might not want to import all the
names from an ontology. To restrict a set of names,
but to preserve the relations between extensions of
the remaining names, we use projection operator (π).
Example 1 Let O
1
= {Teacher Employee, Publica-
tion Achievement}, and assume that O
2
is much
larger and contains axioms like: Book Publication,
Chapter Publication, Monograph Book etc. We
like to reuse O
2
in O
1
, however, in O
2
the notion of
Publication does not include position papers.
Moreover, we find the term Book from O
2
too gene-
ral and do not want to include it the ontology. To
meet our goals we take O
1
′ = O
1
{NPPaper ≡
Publication ŸPositionPaper} and construct M:
M = M(O
1
′) π
S ‒ Book
(ρ
Publication Ø NPPaper
(M(O
2
))).
In Ex. 1 we introduce some intuitive shortcuts to
notation that we also exploit further in the paper. For
example by ρ
A Ø B
we mean that corresponding γ
function changes only the name A to B and by
π
S ‒ X
(M) we mean π
S(M) ‒ {X}
(M). Occasionally for de-
noting names we might use wildcards: e.g. *
Ø 1:*.
While , , ‒ are taken directly from Boolean
algebra of sets,, π and ρ are equivalents of cylindrifi-
cation and substitution from the cylindric algebra
(Henkin, Monk and Tarski, 1971). Any space of
module (class of modules M closed under π, ρ, , ,
‒) can be used to construct a cylindric algebra.
A space of modules can be constructed by
choosing a base space and closing it wrt. π, ρ, , ,
‒. A very natural choice of a base space is {M(α)}
where α is a sentence valid in a selected language L.
Several auxiliary operators can be introduced for
such a space. The selection operator σ is a shortcut
for σ
α
(M) = M M(α). The further two operators
“put under” (υ) and restriction (ξ) are defined below
(I S denotes an interpretation J: Δ
J
= Δ
I
S and
∀X ∈
: X
J
= X
I
S):
L υ
C
M = (S(L) S(M), {I ∈ W(M):
I C
I
∈ W(L)})
(7)
ξ
C
(M) = (S(M), {I C
I
: I ∈ W(M)
I C
I
∈ W(M)})
(8)
“Put under” (Goczyla et al., 2009a) correlates the
domains of two modules by introducing relation-
ships between extensions of terms in L only to a
fragment of M. The restriction operator ξ is an
operator complementing υ. Namely it restricts the
domain of the module to the extension given concept
C. For ALC it may be simply treated as a shortcut
for ξ
C
(M) = σ
C ≡
(M).
Theorem 1. For every module M from M(ALC)
obtained from the basic space {M(α)} with use of
operators (π, ρ, , , σ, υ, ξ) it is decidable whether
the module is satisfiable (i.e. W(M) ≠ ∅).
KEOD 2011 - International Conference on Knowledge Engineering and Ontology Development
268

4 DISTRIBUTED DL
Distributed Description Logics (DDL) is one of the
most prominent modularization methods for DL
ontologies. Originally proposed by Borgida and
Serafini in (2003), it was extended and adapted in
many works. The presentation in this Section is
mainly based on (Homola and Serafini, 2010).
DDLs focus on mapping the terms from a source
module to a target module. We assume there exists a
collection of modules {O
i
}
i ∈ I
, indexed by a set I.
Each module is simply an ontology (it has its local
collection of sentences). Between each pair of
modules O
i
(as a source) and O
j
(as a target; here
and hence in this section i, j ∈ I, i ≠ j) there is
defined a (possibly empty) set of bridge rules μ
ij
.
There are three types of bridge rules (C, D are
concepts and a, b constants, resp. from O
1
and O
2
):
A distributed knowledge base (DKB) ä = ({O
i
},
{μ
ij
}), consists of modules and sets of bridge rules.
Whenever μ
ij
is non-empty, we say that O
j
uses O
i
.
A distributed interpretation à is a pair ({I
i
},
{r
ij
}), where {I
i
} are interpretations (called local in-
terpretation), and {r
ij
} are domain relations between
the domains of I
i
and I
j
. In contrast to standard DL,
each local interpretation might also be a hole, a
special interpretation I
e
with empty domain. A dis-
tributed interpretation à is a model of ä iff for each
i, j ∈ I, we have I
i
O
i
and à μ
ij
. à μ
ij
iff it satis-
fies all the rules μ
ij
according to the following:
DDL exhibits a different behavior than s-modules.
While the latter focuses on importing, DDL focuses
on mapping between terms (this distinction is based
on (Homola and Serafini, 2010)).
While in the basic DDL relation r
ij
might be of
any form, one might consider also more constrained
versions of DDL, denoted by additional symbols:
e.g. F for only functional r
ij
or I for injective r
ij
, e.g.
DDL(F) or DDL(F, I). The following well-known
“penguin” example illustrates the importance of the
relation.
Example 2 (Grau et al., 2004) Let us consider the
ontology O
1
= {Nonflying ≡ ŸFlying, Bird Flying}
and the ontology O
2
= {Penguin }. We define
the mapping μ
12
in the following way:
It might seems that Penguin is unsatisfiable “being
subsumed” by both Nonflying and Bird. But we can
still obtain a non-empty interpretation I
2
in a model
of ä, if the relation r
12
maps at least two individuals
(one Nonflying and one Bird) to a single Penguin.
Originally intended for illustrating cumbersome
behavior of DDL, in fact this example shows its
distinctive capability: to combine knowledge about
several individuals into one. In situations when such
behavior is undesirable we can turn to DDL(F).
5 DDL IN S-MODULE SPACE
In this section we present the results of our work on
expressing DDL in the s-module framework.
Starting from a bit simplified conversion for
DDL(F, I), we gradually move to less constrained
versions of DDL.
5.1 DDL(F, I) with No Cycles
At first we consider a case of DDL(F, I) in which
each individual from Δ
I
i
corresponds to at most one
individual from Δ
I
j
and vice versa.
As it turns out, such assumption significantly
reduces the difficulties of bridging DDL and s-mo-
dules. As a case-study let us consider a distributed
KB ä with two simple DDL-modules O
1
= {C ,
D } and O
2
= {E F} and a set of rules μ
21
=
{2:F 1:C, 2:E 1:D}. Such a mapping implies
that for every model à, I
1
D C.
Despite apparent simplicity of the example,
while analyzing semantics we still have to consider
several possibilities: a domain relation r
21
might map
the whole domain of I
2
to Δ
I
1
, or only a fragment of
a domain of I
2
, or r
21
might even be empty,
resulting in empty interpretation for D. The second
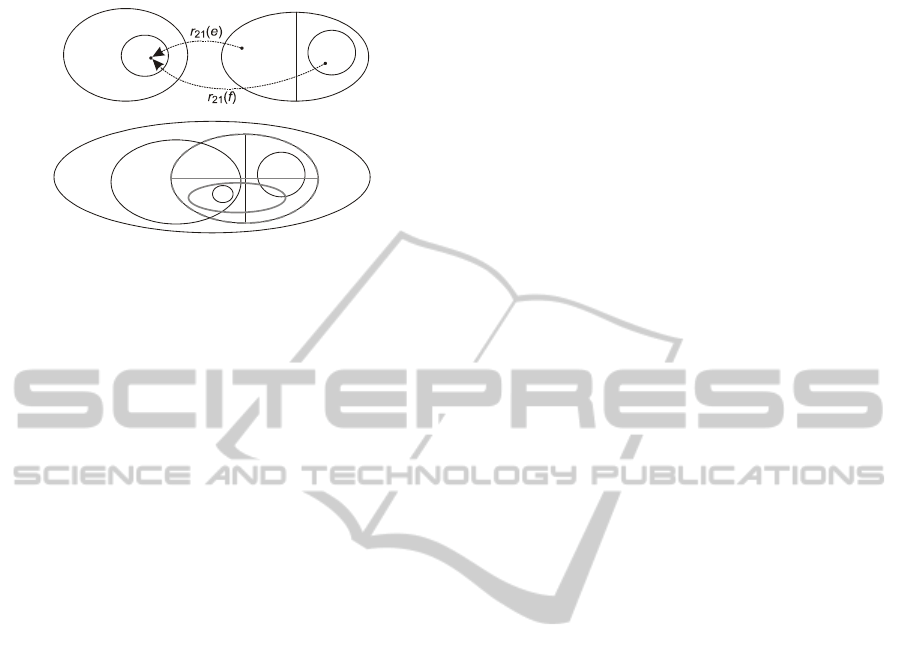
case is depicted in Fig. 1a with use of Venn
diagrams: we can mentally visualize that with
shrinking of r
21
(E
I
2
) the area of D
I
1
is also reduced.
To reflect this effect for s-modules, we have to
simulate the behavior of r
21
. The constructions of a
s-module M
1
representing possible models of O
1
in
ä proceeds as follows. First, we create a s-module
with two special concepts: O
1
and O
2
. Second, we
put under these concepts modules M(O
1
) and M(O
2
)
respectively (if they contain repeating names, we
have to add prefixes). Subsequently, we enforce the
bridge rules by using selection. Then, we project the
signature only to the terms from M(O
1
). Finally, we
1: Bird
2:Penguin
1: Nonflyin
g
2:Penguin
i:
C
j: D (into
b
ridge rule)
i:
C
j: D (onto
b
ridge rule)
i: a ö
j: b (individual correspondence)
à i:
C
j: D iff
r
i
j
(
C
I
i
) ΠD
I
j
à i:
C
j
: D iff
r
i
j
(
C
I
i
)
û D
I
j
à i: a ö
j: b iff
r
i
j
(a
I
i
) d
I
j
ANALYSIS OF MAPPING WITHIN S-MODULE FRAMEWORK
269

restrict the module to the concept O
1
and remove the
concept from the signature.
Figure 1: Different but equivalent effects of DDL(F)
mapping (a) and combining s-modules (b).
The result of the first three steps is depicted in
Fig. 1b. We can see that the outcome gives a similar
effect as in the case of DDL. The area r
21
(Δ
I
2
) is
represented by the intersection O
1
O
2
. Since the
interpretation of the intersection may vary in size,
and may even be empty, all the possible forms of
r
21
(Δ
I
2
) are reflected by models of M. The fact that
r
21
is injective and functional is advantageous here:
each instance of O
1
O
2
represents one element e of
Δ
I
1
and simultaneously one element r
21
‒
(e) of Δ
I
2
.
The procedure sketched above can be general-
ized and formalized as follows:
Definition 2. For a given DKB ä = ({O
i
}, {μ
ij
}),
i, j ∈ I, i ≠ j, a converting function c is a function
that assigns each O
i
a s-module.
Definition 3. A bridge-rule operation β
b
for a bridge
rule b and a module M is:
for b = :
β
b
(M) = σ
α
(M),
α = γ
* Ø i:*
(C) γ
* Ø j:*
(D)
for b = :
β
b
(M) = σ
α
(M),
α = γ
* Ø j:*
(D) γ
* Ø i:*
(C)
for b = i: a ö j: b :
β
b
(M) = γ
i:a Ø j:b
(M)
where by γ(C) we understand a new concept with all
the names substituted with use of γ.
A bridge-rule operation β
μ
for a set of bridge rules
μ and a module M is a composition of β
b
, b ∈ μ.
Definition 4. For given two modules O
i
and O
j
from
a DKB ä, such that O
j
uses O
i
, and a converting fun-
ction c, a s-module integrating O
i
and O
j
wrt. c is:
M
ij
c
= β
μ
ij
(
ρ
* Ø i:*
(c(O
i
)) υ
Ο
i
M({O
i
})
ρ
* Ø j:*
(M(O
j
)) υ
Ο
j
M({O
j
}) )
The construction of the integrating s-module
corresponds to executing the three first steps of the
described procedure (see also Fig. 1b).
Definition 5. For a given DKB ä = ({O
i
}, {μ
ij
}), a
module O
j
, and a converting function c, an integra-
ted s-module for O
j
wrt. c is M
j
c
= …
i ∈ {i: μ
ij
≠ ∅}
M
ij
c
.
A fully integrated module for O
j
wrt. c is FM
j
c
=
ρ
j:* Ø *
(π
S ‒ O
j
(
ξ
Ο
j
(M
j
c
)))
.
The notion of integrated module generalize the
described procedure to the case when more modules
are used. Full integration corresponds to the last two
steps of the procedure. A fully integrated s-module
is indeed useful for describing DDL semantics, as
the following lemma shows.
Lemma 1. For a DKB ä = ({O
i
}, {μ
ij
}), i, j ∈ I,
i ≠ j, expressed in ALC and DDL(F, I), in which O
1
uses all the other modules, and all the other modules
use none, and a converting function c(O
i
) = M(O
i
)
for all i ≠ 1, c(O
1
) = FM
1
c
, a module O
i
is satisfiable
(i.e. for some model it has a local interpretation
which is not a hole) iff c(O
i
) ≠ M({ ^}).
The proof, omitted for brevity, consists of showing
that a model à with non-empty I
1
exists iff there
exists a model of M
1
c
.
The result from Lemma 8 can be generalized to
any acyclic DKB (i.e. DKB ä for which the relation
U
ä
= {(O
i
, O
j
): μ
ij
≠ ∅} forms a forest).
Proposition 1. For any acyclic DKB ä = ({O
i
},
{μ
ij
}), i, j ∈ I, i ≠ j, expressed in ALC and
DDL(F, I), and a converting function c(O
i
) defined
recursively as c(O
i
) = M(O
i
) for leaves, and c(O
i
) =
FM
i
c
for other modules, a module O
i
is satisfiable iff
c(O
i
) ≠ M({ ^}).
With use of Lemma 1 the proof is straightforward,
by induction on each tree of using relation (Lemma
8 forms the induction base, and gives means for
proving the induction hypothesis).
5.2 DDL(F, N
n
) with No Cycles
Here we extend the results from the previous
subsection towards slightly more expressive DDL,
by adapting the introduced notion to the case when
the domain relations are not necessarily injective.
Once again we start with a motivation example.
We adapt the “penguin” example (see Ex. 3). DKB
consists of two modules O
1
= {P }, and O
2
=
{NF ŸF, B NF}, and one non-empty bridge rule
set is: μ
21
= {2:NF 1:P, 2:B 1:P}.
As already mentioned above, the concept P in O
1
may be satisfiable, though for this to happen r
21
has
to map two individuals of Δ
I
2
to a single individual
C
C
O
1
O
1
M
O
2
O
2
D
D
E
E
F
F
a)
b)
i:
C
j: D
i:
C
j: D
KEOD 2011 - International Conference on Knowledge Engineering and Ontology Development
270
of Δ
I
1
. This situation is depicted in Fig. 2a.
Figure 2: Different but (almost) equivalent effects of
DDL(F, N
n
) mapping (a) and combining s-modules (b).
The strategy from the previous section is not
enough to model this situation in the realm of
s-modules. Although we can overlap the domains of
the two modules, simple overlapping (like in Fig.
1b) would render the concept P unsatisfiable. We
have to somehow model the possibility of mapping
two individuals into one.
A solution to this issue is illustrated in Fig. 2b.
The main idea is to apply the conceptual decom-
position twice to the same domain. It can be done
with prefixes (omitted in Fig. 2 for readability),
appropriate s-module operation might look like
M
2.2
= ρ
* Ø 2.2.1:*
(M(O
2
)) ρ
* Ø 2.2.2:*
(M(O
2
). After the
transformation, every element of the domain of (any
model of) M
2.2
represents in fact a pair of elements
of the domain of (some model of) M(O
2
).
There are, however, two issues connected with
this approach. First of all, the constructed module
represent pairs of the original domains. The same
approach can be used to triples, quadruples etc., but
there have to be some known and finite limit to the
cardinality of the tuples. This is the motivation
behind introducing a new constraint for DDL,
namely N
n
, n ∈ N, which implies that every domain
relation r
ij
is at most n-to-one. The discussion in this
section is thus constrained to DDL(F, N
n
).
Second issue is that elements of the domain of
M
2.2
represent in fact some pairs of elements of the
original domain, like (e, e), that we do not want to
include in our considerations. This problem can be
technically overcome (by exploiting disjoint union
satisfiability property of ALC introduced by
Serafini et al. in (2005)), but the discrepancy
between “double overlapping” and pair of domains
still exists, and should be dealt with in future
development of s-module framework (see Sec. 6).
In the following we adapt the notions from the
previous section to the case of DDL(F, N
n
).
Definition 6. A n-bridge-rule operation β
b
n
for a
bridge rule b, a module M and given n is:
for b =:
β
b
(M) = σ
α
(M),
where α is defined below:
α = +
k ∈ [1..n]
+
l ∈ [1..k]
γ
* Ø i.k.l:*
(C) γ
* Ø j:*
(D)
for b = :
β
b
(M) = σ
α
(M),
where α is defined below:
α = γ
* Ø j:*
(D) +
k ∈ [1..n]
+
l ∈ [1..k]
γ
* Ø i.k.l:*
(C)
for b = i: a ö j: b:
β
b
(M) = »
k ∈ 1..n
γ
i.k.1:* Ø j:b
(M)
A n-bridge-rule operation β
μ
n
for a set of bridge
rules μ, a module M and given n is a composition of
β
b
n
for every b ∈ μ.
Definition 7. For given two modules O
i
and O
j
from
a DKB ä, such that O
j
uses O
i
, and a converting
function c, let M be defined as follows:
M = M({O
i.k
O
i.l
^: k, l ∈ [1..n], k ≠ l})
a s-module n-integrating O
i
and O
j
wrt. c is:
n
M
ij
c
= β
μ
ij
n
( ρ
* Ø j:*
(M(O
j
)) υ
Ο
j
M({O
j
})
…
k, l ∈ [1..n], k ≠ l
(
ρ
* Ø i.k.l:*
(c(O
i
)) υ
Ο
i.k.l
M ) )
The pairwisely disjoint concepts O
j.k
represent
k-tuples of elements of the original domain.
Definition 8. For a given DKB ä = ({O
i
}, {μ
ij
}), a
module O
j
, a converting function c, and a number n
an n-integrated s-module for O
j
wrt. c is
n
M
j
c
=
…
i ∈ {i: μ
ij
≠ ∅}
n
M
ij
c
. A fully n-integrated module for O
j
wrt. c is F
n
M
j
c
= ρ
j:* Ø *
(π
S ‒ O
j
(
ξ
Ο
j
(
n
M
j
c
)))
.
Once again we show that fully integrated modules
are equisatisfiable with corresponding modules from
DKB.
Lemma 2. For a DKB ä = ({O
i
}, {μ
ij
}), i, j ∈ I,
i ≠ j, expressed in ALC and DDL(F, N
n
), in which
O
1
uses all the other modules, and all the other
modules use none, and a converting function
c(O
i
) = M(O
i
) for all i ≠ 1, c(O
1
) = F
n
M
1
c
, a module
O
i
is satisfiable iff c(O
i
) ≠ M({ ^}).
The proof, which we omit for brevity, shows that
a model à with non-empty I
1
exists iff there exists a
model of
n
M
1
c
. Again, we can generalize the results
of the lemma to a case of any acyclic DKB.
Proposition 2. For any acyclic DKB ä = ({O
i
},
{μ
ij
}), i, j ∈ I, i ≠ j, expressed in ALC and
DDL(F, N
n
), and a converting function c(O
i
) defined
recursively as c(O
i
) = M(O
i
) for leaves, and c(O
i
) =
F
n
M
i
c
for other modules, a module O
i
is satisfiable
iff c(O
i
) ≠ M({ ^}).
Proof (sketch): Analogously like in proof for Prop.
1, but with use of Lemma 13.
P
O
1
M
O
2
O
2
O
1
B
B
P
NF
NF
NF
F
B
F
F
a)
b)
f
e
p
i:
C
j
: D
i:
C
j: D
ANALYSIS OF MAPPING WITHIN S-MODULE FRAMEWORK
271

5.3 Decidability
The discussion from the previous points gives us
also means for creating a procedure for deciding
satisfiability of modules in a DKB.
The decidability result from Th. 1 combined with
Prop. 2 allows for immediate stating that DDL(F,
N
n
) is decidable for acyclic DKBs. However, we can
extend this result a bit by including the DKBs which
can contain cycles.
A basic idea behind such extention is simple: we
proceed iteratively with determining c(O
i
) for each
module, assuming that in first iteration c
1
(O
i
) =
M(O
i
) and then, in the next k-th iteration taking
c
k
(O
i
) = F
n
M
i
c
k ‒ 1
(O
i
). As Serafini and Tamilin show
in (2007), the fixpoint will finally be reached, which
can be detected by adapted procedure for checking
whether an ontology is a conservative extension of
another (Lutz, Walther and Wolter, show in (2007)
that this problem for ALC is decidable).
This leads us to the following conclusion:
Proposition 3. For a given DKB ä = ({O
i
}, {μ
ij
}),
i, j ∈ I, i ≠ j, an recursive procedure for converting
modules in the following way: c
1
(O
i
) = M(O
i
), c
k
(O
i
)
= F
n
M
i
c
k ‒ 1
(O
i
), repeated until c
k
(O
i
) is a conservative
extension of c
k ‒ 1
(O
i
) for all i ∈ I, is a terminating,
sound and complete procedure for deciding satisfia-
bility of modules for ALC and DDL(F, N
n
).
6 CONCLUSIONS
In this section we summarize the main observations
and contributions of the paper and relate them to
other studies.
From the point of view of DDL, the results
allows us to show some insight in the relation
between mapping and importing (Homola and
Serafini, 2010). Here we show how different kinds
of mappings relate to specific kinds of importing
(especially “putting under”). Further work will allow
us to include also E-Connection (Kutz, Lutz,
Wolter, and Zakharyaschev, 2004) and P-DL (Bao,
Voutsadakis, Slutzki, and Honavar, 2009), two other
major methods of modularization.
The other result is an alternative way of proving
decidability of DDL(F, N
n
) for ALC. Though at the
current stage of research it does not extend the
results already available in literature, it shows the
practical application of the results from Th. 1. The
further development might result in a set of
techniques for proving decidability for a wide range
of modularization methods.
From the perspective of s-module framework the
presented discussion provides interesting hints about
its further development. The s-module framework
cannot easily handle situations in which we want to
refer to a tuple of elements of a domain. Sec. 5.3
suggests it may be useful to extend the framework
by some kind of treatment for limits (i.e. the ability
to determine bounds for an arbitrary set of modules).
Finally, the paper presents some extensions to
the framework of s-modules: definition of s-module
space, restriction operator, and a slightly extended
result for decidability (cf. Sec. 3).
ACKNOWLEDGEMENTS
This work is partially supported by the Polish
National Centre for Research and Development
under Grant No. SP/I/1/77065/10 by the strategic
scientific research and experimental development
program: „Interdisciplinary System for Interactive
Scientific and Scientific-Technical Information”.
REFERENCES
Bao, J., Voutsadakis, G., Slutzki, G. & Honavar, V.
(2009). Package-Based Description Logics. In:
Modular Ontologies. Springer: Berlin Heidelberg.
Borgida, A. & Serafini, L. (2003). Distributed Description
Logics: Assimilating Information from Peer Sources.
J. Data Semantics, 1, 153-184.
Grau, B. C., Parsia, B., & Sirin, E. (2004). Working with
Multiple Ontologies on the Semantic Web. In: The
Semantic Web – ISWC 2004 (pp. 620-634).
Goczyla, K., Waloszek, A. & Waloszek, W. (2009a).
S-modules - Approach to Capture Semantics of
Modularized DL Knowledge Bases. Proc. of KEOD
2009 (pp. 117-122).
Goczyla, K., Waloszek, A. & Waloszek, W. (2009b) A
Semantic Algebra for Modularized Description Logics
Knowledge Bases. Proc. of DL 2009.
Homola, M. & Serafini, L. (2010). Towards Formal
Comparison of Ontology Linking, Mapping and
Importing. Proc. of DL2010.
Kutz, O., Lutz, C., Wolter, F. & Zakharyaschev, M.
(2004). E-connections of abstract description systems.
Artificial Intelligence, 156(1), 1-73.
Lutz, C., Walther, D. & Wolter, F. (2007). Conservative
extensions in expressive description logics. Proc. of
IJCAI-2007, 453-459. doi:10.1.1.117.2884.
Serafini, L., Borgida, A. & Tamilin, A. (2005). Aspects of
Distributed and Modular Ontology Reasoning. In
Proc. of IJCAI 2005, pp. 570-575.
Serafini, L. & Tamilin, A. (2007). Aspects of Distributed
and Modular Ontology Reasoning. Technical report.
KEOD 2011 - International Conference on Knowledge Engineering and Ontology Development
272
