SUITABILITY OF A GENETIC ALGORITHM FOR ROAD

TRAFFIC NETWORK DIVISION

Tomas Potuzak

Department of Computer Science and Engineering, University of West Bohemia, Univerzitni 8, Plzen, Czech Republic

Keywords: Traffic Network Division, Genetic Algorithm, Multi-objective Optimization.

Abstract: In this paper, the suitability of a genetic algorithm as a part of a method for division of road traffic network

is discussed. The division of traffic network is necessary during the adaptation of the road traffic simulation

for distributed computing environment. This environment enables to perform detailed simulation of large

traffic networks (e.g. entire cities and larger) in a reasonable time. Genetic algorithms are considered, since

they are often employed in both graph partitioning and multi-objective optimization problems. These

problems are closely associated with the problem of road traffic network division.

1 INTRODUCTION

The computer simulation of road traffic is an

important tool for analysis and control of road traffic

networks. However, a detailed simulation of large

areas (e.g. entire cities) can still require unsuitable

amount of computational time. Therefore, many

simulators have been adapted for distributed

computing environment (Nagel and Rickert, 2001,

Gonnet, 2001). In this environment, the combined

power of multiple interconnected computers (nodes)

is utilized to speed up the simulation. The traffic

network is divided into sub-networks, which are

then simulated by simulation processes running on

particular nodes of the distributed computer.

The division of the network can affect the

performance of the resulting distributed simulation.

There are two main issues, which should be

considered during the simulation – the similar load

of the simulation processes and minimal inter-

process communication among them. There are

many methods for division of traffic network, which

consider one of the issues, both, or neither.

In this paper, the suitability of a genetic

algorithm (GA) as a part of a method for division of

road traffic network is discussed. Genetic algorithms

are considered, since they are often employed in

both graph partitioning (Menouar, 2010) and multi-

objective optimization (Farshbaf and Feizi-Darakh-

shi, 2009) problems, which are closely associated

with the problem of road traffic network division.

2 TRAFFIC NETWORK

DIVISION

As it was said, there are two issues, which should be

considered during the traffic network division. Both

issues are described in following subsections.

2.1 Load-balancing of Sub-networks

The similar load of the simulation processes is

necessary, because all simulation processes are

synchronized. Hence, the maximal speed of the

simulation is determined by the slowest process

(Cetin et al., 2003). So, the distributed simulation

can achieve maximal speed, when the load of all

simulation processes is similar and all processes

require similar time to be performed.

The load of the simulation processes depends

primarily on the number of vehicles moving within

the simulated sub-networks. The reason is that the

movement of the vehicles is the primary and most

computation-consuming activity of the simulation.

If the load-balancing issue is considered during

the traffic network division, the common approach is

to use some feature of the traffic network as a

representative weight for the load of the network.

The network is then divided in a way that the sub-

networks have similar weights, whose sum is equal

to the weight of entire traffic network. The weight

can be for example cumulative length of traffic lanes

(Nagel and Rickert, 2001) or number of vehicles

448

Potuzak T..

SUITABILITY OF A GENETIC ALGORITHM FOR ROAD TRAFFIC NETWORK DIVISION.

DOI: 10.5220/0003657204400443

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 440-443

ISBN: 978-989-8425-79-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

moving within the lanes (Gonnet, 2001).

2.2 Low Inter-process Communication

The minimal inter-process communication is neces-

sary, because it is relatively slow in comparison to

other activities in the distributed simulation. The

communication is required for the transfer of

vehicles between the particular neighbouring traffic

sub-networks and also for synchronization.

The number of messages for vehicles transfer is

affected by the number of traffic lanes inter-

connecting the traffic sub-networks. Therefore, it is

convenient to minimize this number during the

traffic network division. Graph partitioning methods

such as orthogonal recursive bisection can be emp-

loyed for this purpose (Nagel and Rickert, 2001).

3 GENETIC ALGORITHMS (GA)

Now, as we discussed traffic network division

issues, we can proceed with genetic algorithms.

3.1 General Concept

Genetic algorithms (GA) are evolutionary algo-

rithms that mimic natural genetic evolution and

selection in nature (Menouar, 2010). Developed by

John Holland at the University of Michigan

(Holland, 1975), they are widely used for solving of

searching and optimization problems in many

domains including multi-objective optimization

(Farshbaf and Feizi-Darakhshi, 2009).

3.2 Basic Phases and Notions

Using a genetic algorithm, it is first necessary to

define representation of a problem solution. Usually,

a solution or an individual is represented by a vector

of binary or integer values. When the representation

is specified, an initial set of individuals is generated.

This set is called initial population (Menouar, 2010).

For all individuals of the set, a fitness function is

calculated. This function represents an assessment of

the individual (Menouar, 2010) depending on pro-

blem domain. It can favour one criterion or be multi-

objective (Farsh-baf and Feizi-Darakhshi, 2009).

A number of individuals with best fitness are

selected. The crossover and mutation are then used

to produce a new population (Farshbaf and Feizi-

Darakhshi, 2009). By crossing, a new offspring is

produced using two parents. The mutation is

represented by random change(s) in the individual’s

representation (Bui and Moon, 1996).

The whole process repeats until certain number

of iterations is reached (Menouar, 2010) or a stop

condition is fulfilled (Bui and Moon, 1996).

4 GA FOR NETWORK DIVISION

Genetic algorithms should be suitable for traffic

network division, since they are convenient for

graph partitioning and multi-objective optimization.

The equal load of the simulation processes and

minimal number of connecting traffic lanes between

them are the two objectives of the network division.

4.1 Problem Formulation

The genetic algorithm can optimize both criterions

using the correct fitness function. Its input is the

traffic network, which shall be divided into required

number of sub-networks. Moreover, for the load-

balancing of the sub-networks, it is necessary to add

information about the vehicles, because the load of

the sub-networks depends primarily on the number

of vehicles moving within them (see Section 2.1).

4.2 Assigning Weights to Traffic Lanes

The information about the vehicles can be added as

the weights of particular traffic lanes. These weights

express the mean number of vehicles moving in the

lanes during the simulation run.

However, the acquisition of this information

from the sequential run of the simulation can be

problematic due to memory and time requirements.

Still, this approach can be found in (Gonnet, 2001).

Another solution is to use a less detailed

simulation, which is fast enough to be performed

sequentially in a suitable time. The fidelity of such

less-detailed simulation is lower than the fidelity of

the simulation, but sufficient to be used for the

network division (Potuzak, 2011).

4.3 Dividing Network using GA

So, the genetic algorithm has the weighted traffic

network as its input. Its output is the assignment of

the crossroads to the particular sub-networks. This

information is sufficient for marking of traffic lanes,

which shall be divided to form the required number

of sub-networks (the ultimate goal of the traffic

network division). It is only necessary to mark

traffic lanes connecting crossroads assigned to

different sub-networks (Potuzak, 2011).

SUITABILITY OF A GENETIC ALGORITHM FOR ROAD TRAFFIC NETWORK DIVISION

449

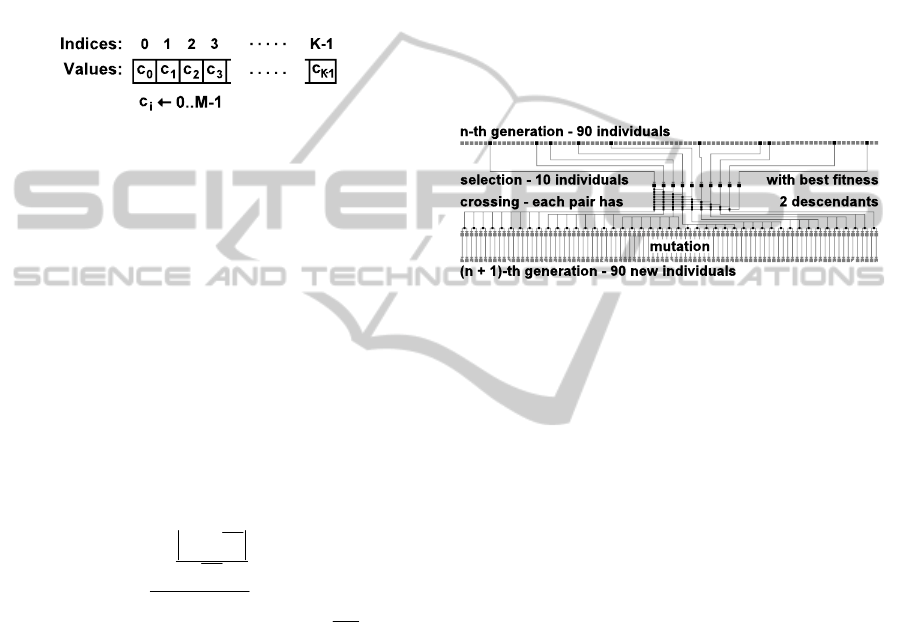
4.4 Representation of Individual

The first step in design of a genetic algorithm is to

determine the representation of an individual. In this

case, an individual can be represented by a vector of

integers with the size corresponding to the total

number of crossroads K. Then, each vector index

represents a crossroad and its value represents the

sub-network, to which the crossroad is assigned (see

Fig. 1). So, the maximal value of an integer cor-

responds to the number of required sub-networks M.

Figure 1: Representation of an individual.

In the initial population of 90 individuals, the

crossroads are randomly assigned to the sub-

networks. Using the fitness function, crossover, and

mutation, this assignment changes towards a

solution, where the sub-networks are load-balanced

and the number of divided lanes is minimal.

4.5 Fitness Function

Considering the statements from previous sections,

the fitness function consists of two parts – the

equability representing the equal load of the sub-

networks and the compactness representing the

minimal number of divided traffic lanes. The

equability of an individual can be calculated as:

Si S

−

=−

∑

(1)

where E is the equability of an individual,

w is the

mean total weight of one traffic sub-network, w

the total weight of the ith sub-network, and M is the

number of sub-networks.

The compactness C is very important for minimi-

zation of the number of divided traffic lanes. It can

be calculated as the ratio of the number of undivided

traffic lanes and the total number of traffic lanes.

Due to different requirements for the traffic

network division results in different situations, it is

possible to set the equability ratio in the fitness

function. Hence, it can be calculated as:

()

CrErF

⋅

−

+⋅= 1 ,

(2)

where, F is the fitness function of an individual, E is

its the equability, C is its compactness and r

is the

ratio of the equability in the fitness function. The r

can be set from 0.0 to 1.0. For a standard situation,

the r

has the value from 0.25 to 0.5.

4.6 Crossover and Mutation

After the initial population of 90 individuals is

generated (see Section 4.4), the fitness value is

calculated for each individual. Based on the fitness

value, 10 individuals are selected to be “parents” of

the next generation. The size of population and the

number of selected individuals have been selected

based on preliminary tests. The next generation is

created using the crossover and mutation operators

on the selected individuals (see Fig. 2).

Figure 2: Creation of new generation of individuals.

Using all combinations of 10 selected indivi-

duals, a new generation of 90 individuals is created

and the entire process repeats until preset number of

generations is reached.

5 TESTS AND RESULTS

The suitability of the genetic algorithm for traffic

network division was tested. Two sets of tests were

performed as described in following sections.

5.1 Fitness Dependencies

The first set of tests was focused on the dependen-

cies of the maximal achieved fitness on the size of

the traffic network, the number of sub-networks, and

the number of generations. Three regular square

grids of 64, 256, and 1024 crossroads divided into 2,

4, and 8 sub-networks were used for testing. The

number of generations ranged from 100 to 100000.

The r

ratio was set to 0.5.

The results (averaged from ten attempts) are

depicted in Fig. 3. The maximal achieved fitness

increases with increasing number of generations.

This is an expectable behaviour, since more genera-

tions offer more time for convergence to the best

solution. Another observation is that the maximal

achieved fitness decreases with increasing number

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

450

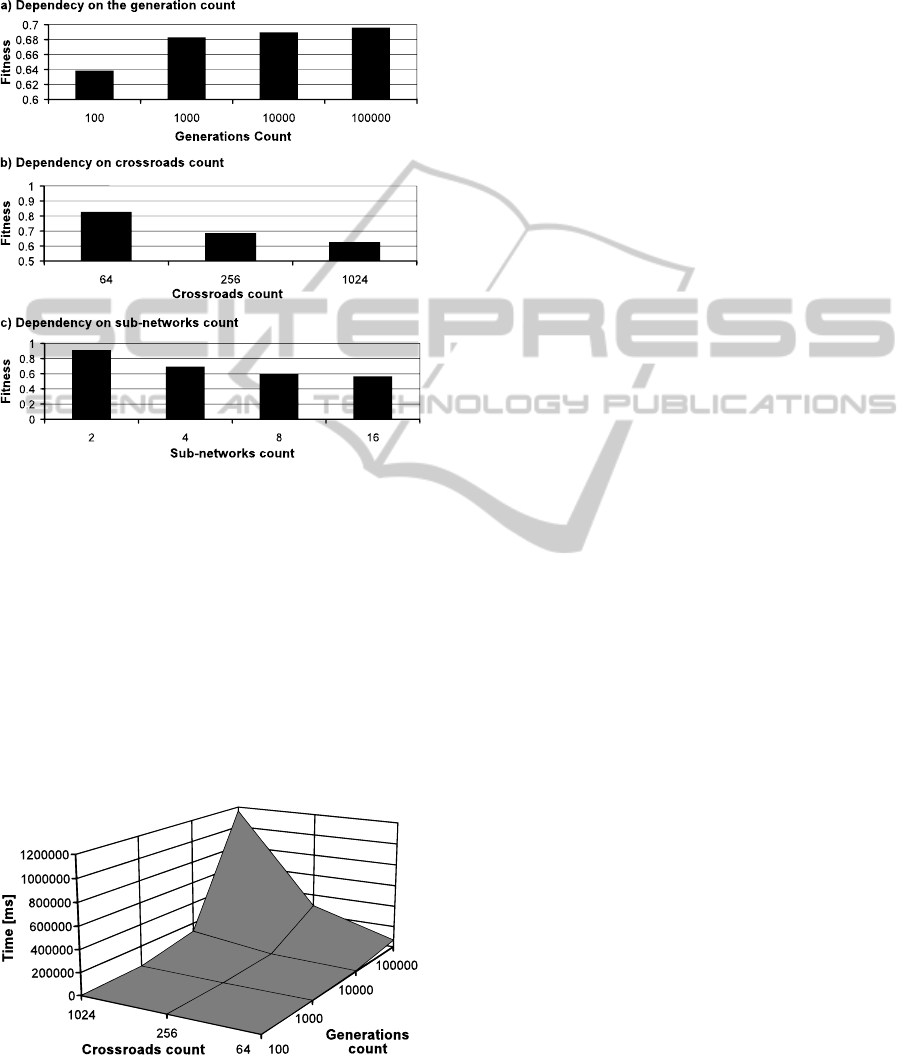
of crossroads and sub-networks. This is caused in

both cases by higher complexity of the individuals

due to increasing length or increasing number of

possible values in the individuals, respectively.

Figure 3: Dependencies of the maximal achieved fitness.

5.2 Time Performance of the GA

The second set of tests was focused on the time

performance of the genetic algorithm, which

depends on both the size of the traffic network and

the number of generations. It was tested using a

regular square grid of 64, 256, and 1024 crossroads,

respectively. For each traffic network, the genetic

algorithm was performed using 100, 1000, 10000,

and 100000 generations. The network was always

divided into two sub-networks. Both dependencies

can be observed in Fig. 4.

Figure 4: Dependency of the GA time performance.

Both time dependencies on the network size and

generations count are linear (note logarithmic scale

of the x- and y-axis and linear scale of the z-axis).

6 CONCLUSIONS

In this paper, we discussed the suitability of a

genetic algorithm for division of the weighted traffic

network. Considering the results of the performed

sets of tests, it can be concluded that the genetic

algorithm is suitable for the traffic network division.

Its computation time is linearly dependent on the

size of traffic network and the number of generation

count. This makes it usable even for large networks.

In our future work, we will focus on further

improvements of the designed genetic algorithm.

ACKNOWLEDGEMENTS

This work is supported by the Ministry of Education,

Youth, and Sport of Czech Republic – University

spec. research – 1311.

REFERENCES

Bui, T. N., Moon, B. R., 1996, Genetic Algorithm and

Graph Partitioning. In: IEEE Transactions on

Computers, vol. 45(7).

Cetin, N., Burri, A., Nagel, K., 2003, A Large-Scale

Agent-Based Traffic Microsimulation Based on Queue

Model. In: Proceedings of 3rd Swiss Transport

Research Conference, Monte Veritas.

Farshbaf, M., Feizi-Darakhshi, M., 2009, Multi-objective

Optimization of Graph Partitioning using Genetic

Algorithms. In: 2009 Third International Conference

on Advanced Engineering Computing and

Applications in Sciences.

Gonnet, P. G., 2001, A Queue-Based Distributed Traffic

Micro-simulation. Technical report.

Holland, J. H., 1975, Adaptation in Natural and Artificial

Systems. University of Michigan Press, Ann Arbor.

Menouar, B., 2010, Genetic Algorithm Encoding

Representations for Graph Partitioning Problems. In:

2010 International Conference on Machine and Web

Intelligence (ICMWI), pp. 288–291.

Nagel, K., Rickert, M., 2011. Parallel Implementation of

the TRANSIMS Micro-Simulation. In: Parallel

Computing, vol. 27(12), pp. 1611–1639.

Potuzak, T., 2011, Comparison of Road Traffic Network

Division Based on Microscopic and Macroscopic

Simulation. In: UKSim 2011 – UKSim 13th

International conference on Computer Modelling and

Simulation, Cambridge, pp. 409–414.

SUITABILITY OF A GENETIC ALGORITHM FOR ROAD TRAFFIC NETWORK DIVISION

451