COLLECTIVE DECISION UNDER PARTIAL OBSERVABILITY
A Dynamic Local Interaction Model
Arnaud Canu and Abdel-Illah Mouaddib
Universit
´
e de Caen Basse-Normandie, UMR 6072 GREYC, F-14032 Caen, France
CNRS, UMR 6072 GREYC, F-14032 Caen, France
Keywords:
Markovian decision process, Game theory and applications, Multiagent decision making, Co-operation.
Abstract:
This paper introduces DyLIM
a
, a new model to describe partially observable multiagent decision making
problems under uncertainty. DyLIM deals with local interactions amongst the agents, and build the collective
behavior from individual ones. Usually, such problems are described using collaborative stochastic games,
but this model makes the strong assumption that agents are interacting all the time with all the other agents.
With DyLIM, we relax this assumption to be more appropriate to real-life applications, by considering that
agents interact sometimes with some agents. We are then able to describe the multiagent problem as a set of
individual problems (sometimes interdependent), which allow us to break the combinatorial complexity. We
introduce two solving algorithms for this model and we evaluate them on a set of dedicated benchmarks. Then,
we show how our approach derive near optimal policies, for problems involving a large number of agents.
a
This work is supported by the DGA (Direction G
´
en
´
erale de l’Armement, France).
1 INTRODUCTION
Decision making under uncertainty is an important as-
pect of Artificial Intelligence. Its extension to mul-
tiagent settings is even more important to deal with
real-world applications such as multirobot systems or
sensor networks for example. Stochastic games are
useful to describe such problems, especially the spe-
cific case of cooperative agents, represented by DEC-
POMDPs. However, this model is very hard to solve
because of the significant number of different situa-
tions each agent can face. Furthermore, this model is
based on the strong assumption that each agent is in-
teracting with all the other agents, at anytime. For this
reason, its a NEXP-Complete problem
1
.
Recently, other models were introduced, relaxing
this assumption. They are based on the idea that
an agent only interacts sometimes, with some other
agents (local interactions). However, they all suffer
from limitations in terms of applicability. Some ap-
proaches use a static interaction model, meaning that
the agent is always interacting with the same agents.
Other approaches use a dynamic interaction model
1
NEXP is the set of decision problems that can be solved
by a non-deterministic Turing machine using time O(2
p(n)
)
for some polynomial p(n), and unlimited space.
but limit the possible interactions (using coordination
locales with task allocation, or needing free commu-
nication and full local observability).
Our work is motivated by the practical problem of
a group of autonomous vehicles evolving in an envi-
ronment where they cannot communicate. The agents
are able to observe their neighbors, so they take deci-
sions based on local interactions: the existing models
are unable to formalize such problems. In this paper,
we introduce a new model (Dylim, the Dynamic Lo-
cal Interaction Model) to describe problems involving
local interactions with a dynamic interaction model,
with partial observability and no communications.
We describe our approach to compute a near-
optimal policy for a given agent, using our model.
First, we give an algorithm which extract the deci-
sion making problem of the agent, from the multia-
gent problem. Then, we give a second algorithm able
to solve this decision making problem. Finally, we
present the performance of these techniques, with ex-
perimental results using the existing dedicated bench-
marks. For each benchmark, we compare the quality
of our policies with the underlying MMDP, we show
the efficiency of our approach and how we can scale
up to large problems with good computation times.
146
Canu A. and Mouaddib A..
COLLECTIVE DECISION UNDER PARTIAL OBSERVABILITY - A Dynamic Local Interaction Model.
DOI: 10.5220/0003643801460155
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 146-155
ISBN: 978-989-8425-83-6
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

2 BACKGROUND
This study concerns the scalability of DEC-POMDPs
(which are cooperative stochastic games) by using a
different point of view on how to solve them and over-
come the curse of dimensionality. For this purpose,
we introduce DEC-POMDPs as the classic model
for partially observable multiagent decision making.
Then, we introduce POMDPs (Cassandra et al., 1994)
and Q-MDPs as models for monoagent problems with
partial observability and MMDPs (Boutilier, 1996) as
a model for multiagent problems model with full ob-
servability: we will use those two frameworks.
2.1 Stochastic Games
A stochastic game (Shapley, 1953) is defined by a
tuple hI, S, A, R, T i with (1) I the number of play-
ers in the game, (2) S a set of states in which the
game can be (each state being similar to a classical
game with I players), (3) A = A
1
× A
2
× . . . × A
I
a
set of joint actions (A
i
=
n
a
1
i
, . . . , a
|
A
i
|
i
o
the actions
player i can do), (4) R =
{
R
1
, R
2
, . . . , R
I
}
the set of
reward functions (R
i
: S ×A → R the reward func-
tion of player i which gives, in each state, the posi-
tive or negative reward associated to each joint action)
and (5) T : S × A × S → [0, 1] the joint transition
function (T (s, a, s
0
) the probability for the I players
applying an action a in a state s to move to a state s
0
).
Players can know the actual state, or only know
a probability distribution over a subset of possible
states. At each step, each player i chooses an action
from its set A
i
, based on the actual state s and on its
policy π
i
. The game then moves to a new state s
0
.
The joint policy is given by π = (π
1
, . . . , π
I
).
2.2 Decentralized Partially Observable
Markovian Decision Processes
DEC-POMDP (Bernstein et al., 2000) is a model for-
malizing cooperative multiagent decision-making in
partially observable environments. A DEC-POMDP
is a specific stochastic game, described with a tu-
ple hI, S, A, T, R, Ω, Oi, where each player is called an
“agent”, S = {s
1
, . . . , s
k
} is a set of k joint states (∀i, s
i
j
is the individual state of agent j) and A = {a
1
, . . . , a
l
}
and T are similar to a stochastic game. There is only
one reward function R : S×A×S → R (we could write
R = R
1
= R
2
= . . . ) and we add Ω = {o
1
, . . . , o
j
} a
set of joint observations the agents can receive about
the environment and O : S × A × S × Ω → [0;1] an
observation function giving the probability to re-
ceive an observation o ∈ Ω after a transition s →
a
s
0
.
The main difference, with a “standard” stochas-
tic game, is that we only have one reward function
R for all the agents, instead of one per agent. The
agents are then cooperative, because they are opti-
mizing the same reward function. Solving a DEC-
POMDP means computing a joint policy π which
gives, at any moment, the joint action a ∈ A the agents
will have to apply. We call history the sequence
(a
0
, o
0
, a
1
, o
1
, . . . ) of actions and observations done
by the agents from the beginning of the execution.
If we write H the set of all possible histories, a pol-
icy will be a function π : H → A. Moreover, if we
have a usable criterion to evaluate a given policy, we
can compute an optimal policy π
∗
. Solving a DEC-
POMDP is done by computing the optimal joint pol-
icy: the time complexity is NEXP-complete (Bern-
stein et al., 2000), which is very hard. Until now,
existing algorithms only work on problems with lim-
ited agents, reducing their applicability for real world
problems. The aim of our framework is to build a new
model, able to solve larger problems, by breaking the
complexity of a DEC-POMDP.
2.3 POMDP and Q-MDP
POMDPs are used to describe partially observable
monoagent planning problems under uncertainty: we
can see a POMDP as a specific DEC-POMDP, where
I = 1. A POMDP is a tuple hS, A, T, R, Ω, Oi such
that those elements are similar to a DEC-POMDP,
in the monoagent settings. POMDPs have an in-
teresting property: a history can be replaced by a
belief-state b which is a probability distribution
over S with b(s) the probability to be in s. Belief-
states are very hard to compute for DEC-POMDPs.
Solving a POMDP is a hard problem, so Q-
MDPs (Littman et al., 1995) were introduced in or-
der to simplify this task. The basis of Q-MDPs is
to solve the underlying MDP and to compute a Q-
value function Q
MDP
: S × A → R. Then we can write
∀b, a : Q(b, a) =
∑
s∈S
b(s).Q
MDP
(s, a). It is then pos-
sible to extract from Q a policy π for the POMDP.
However, such an approach is not exact, because we
overestimate the value of each state (with the wrong
hypothesis that we are able to act optimally with a full
observability) and we underestimate the value of the
epistemic actions (actions modifying the belief only,
and not the environment).
2.4 Fully Observable Problems:
Multiagent MDPs
A fully observable problem is such that an agent
alone can know its state at any moment, so we don’t
COLLECTIVE DECISION UNDER PARTIAL OBSERVABILITY - A Dynamic Local Interaction Model
147

need to use observations. MMDPs (Boutilier, 1996)
are able to describe a multiagent fully observable
problem with a tuple hI, S, A, T, Ri (those elements
are similar to a DEC-POMDP). Solving an MMDP
means computing a joint policy π : S → A. In or-
der to compute this policy, we use the classical Bell-
man operator: for each state, we compute an optimal
value function V
∗
(s). Using it, we compute π
∗
(s) =
argmax
a∈A
∑
s
0
∈S
T (s, a, s
0
).[R(s, a, s
0
) + γV
∗
(s
0
)] with
0 ≤ γ < 1. It is usually possible to write π =
{π
1
, . . . , π
I
} with π
i
the policy of the agent i (from in-
dividual states to individual actions). The time needed
to compute such a joint policy grows polynomially
with |S| the number of states, but |S| grows exponen-
tially with the number of agents.
3 RELATED WORKS
Recently, a lot of work has been developed to over-
come the curse of dimensionality and scale par-
tially observable multiagent problems to more than
2 agents, using interaction-based models. However,
these models bring a new difficulty: if we make the
assumption that agents interact only sometimes, with
some other agents (local interactions), then we need
to detect when these interactions occur. Some ap-
proaches use tasks allocation (Varakantham et al.,
2009), a subclass of multiagent decision making. In
the general case, the most promising works make
strong assumption to detect these interactions, and
thus suffer from limitations in terms of applicability.
3.1 Static Interaction Models
The ND-POMDP model (Nair et al., 2005; Kumar
and Zilberstein, 2009) was introduced to describe
problems with local interactions. Using this model,
one can solve large problems, but is limited by two
strong assumptions. First, ND-POMDPs address
problems with a static interaction structure, meaning
that an agent is always interacting with the same set
of neighbors. Second, this model can only deal with
dependencies over rewards, but not over transitions.
More recently, good results were achieved using
Factored-DEC-POMDPs (Oliehoek et al., 2008). It
is able to solve problems with more than two agents
while keeping dependencies between agents. How-
ever, those studies are based on the same kind of prob-
lems as ND-POMDPs, with static interactions.
3.2 Task-based Interaction Models
Distributed POMDPs can be used to describe multia-
gent problems, using coordination locales (Varakan-
tham et al., 2009). Using such an approach, the agents
are mainly independent, but share a set of tasks which
can be done or not, and transition and reward func-
tions depend not only on the state of the agent, but
also on the set of tasks. Moreover, an agent does not
observe anything about the other agents, but receive
observations about tasks (and about its own state).
Using such a model, it is possible to deal with a lot
of agents, with the solving process being highly de-
centralized. However, this model describes problems
with a task allocation component. Such problems are
only a subclass of multiagent decision making, and a
lot of other problems need more complex interactions.
3.3 Dynamic Interaction Models
The IDMG model (Spaan and Melo, 2008) was in-
troduced to describe problems with local interactions,
like ND-POMDPs, but with a dynamic interaction
model. Using IDMGs, one can describe large prob-
lems with dependencies between agents, and is no
more limited to static interactions: each agent inter-
acts with an evolving set of agents. Moreover, using
this model, Spaan et al. were able to compute near-
optimal policies on a set of dedicated benchmarks.
However, this model introduces new strong as-
sumptions. First, each agent has to know its own
state (it is a full local observability). Second, an agent
can use unlimited and free communication with the
agents it is interacting with. So, the sub-problem of
a given interaction becomes fully observable. Then,
the problems addressed by this solver are not similar
to DEC-POMDPs but are a good threshold between
DEC-POMDPs and MMDPs. Our approach is simi-
lar to IDMG, extended to partial observability.
4 THE MODEL: DYLIM
Our goal, with the DyLIM, is to describe multiagent
decision making problems with no assumption (ex-
cepted the idea that wa can give a finit set of all the
possible interactions between two agents). We deal
with dependencies over transitions, rewards and ob-
servations. Moreover, we deal with partial observ-
ability, over the state of the agent and over the other
agents. Finally, we use a dynamic interaction model
without needing any communication between agents.
In this section, we introduce our model and how to use
it, to describe a multiagent decision making problem.
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
148

4.1 Local Interactions
DyLIM is built on a simple idea: it is not always nec-
essary to consider all the agents as fully dependent of
each other. For example, in a group of robots evolving
in a given environment, each has to move to a given
point while observing the neighbors so they don’t col-
lide. However, the agent does not need to remember
the positions of the agents outside the neighborhood.
So, in a given state, an agent is only interacting with
a subset of the I agents involved in the problem.
Such a model deals with multiple kind of applica-
tions. We will focus on examples derived from those
described in (Spaan and Melo, 2008). We consider the
ISR problem where I agents evolve into a map (fig.1).
In this problem, two agents start at a random position
and have to reach a given target (the two ’X’ in fig.1).
The agents must not be in the same place at the same
moment. An agent receives observations about walls
surrounding it and about the relative position of the
other agent, but observation accuracy decreases with
the distance. We will use the ISR problem as an ex-
ample in the following sections.
4.2 Main Idea
We can split a multiagent problem into two parts. The
first one describes the individual problem, used for a
single agent “ignoring” the other agents (with fully
independent transition, reward and observation func-
tions). In ISR, it describes how the agent evolves in
the map, gets observations about the walls and re-
ceives a reward when it reaches its target. The sec-
ond part of the problem describes its coordination as-
pect: how the agent influences the agents with which
it is in interaction (we call those agents interacting
agents). In ISR, it describes how the agent gets ob-
servations about its neighbors, how they evolve and
how a negative reward is received when colliding.
This second part is described by relations between
the agent and its interacting agents, observations the
agent can receive about those relations and joint func-
tions (rewards and transitions) describing how those
relations will evolve. Finally, the problem is a cou-
ple Pb = (< individual >, < coordination >). We
only have to solve those two problems, and to ex-
tract a solution for the global problem, so we can
give for each state s a vector-value function V (s) =
(V
ind
(s),V
coo
(s)). Figure 2 describes this principle.
4.3 Individual Part
This part is a classical POMDP. We represent the
planning problem of a single agent with a tu-
Figure 1: The ISR problem.
problem
individual
part
coordination
part
solution
solution
global
solution
Figure 2: General idea.
ple hS, A, T, R, Ω, Oi which will be solved with any
POMDP solver. This part is exact for states where the
agent has no interaction, but could induce mistakes
on transitions, rewards or observations for states with
interactions. Then, we use the “coordination” part.
4.4 Coordination Part
We show in this section how the coordination problem
of an agent i with all its interacting agents is described
with a tuple hSR, ΩR, OR,Ci.
4.4.1 SR: Relations
SR is a set of relations, describing how an agent
ag
k
can be interacting with agent ag
i
.
Definition 1 (Relation). A relation R
l
describes a
property l between a state of ag
i
and one of its in-
teracting agents ag
j
: R
l
= {(s
i
, s
j
)|l(s
i
, s
j
) = True}
We write SR = {R
1
, . . . , R
|SR|
} the set of all pos-
sible relations and we have: ∀R
l
, R
k
∈ SR, R
l
∩R
k
=
/
0. In the ISR example, one relation will be Front,
meaning an agent j is in front of agent i. When an
agent ag
i
, in a state s
i
, perceives an interacting agent
ag
j
, it can build the couple (s
i
, s
j
) and find the asso-
ciated relation R . Then, we say this relation is the
relative state rs
j
of agent ag
j
.
According to this definition, a joint relative state
rs is such that rs = (rs
1
, . . . , rs
k
) with rs
j
the relative
state associated to agent j. In the ISR problem, we
imagine that an agent i (in state s
i
= (x2, y3)) detects
an agent j in front of him (s
j
= (x2, y4)). We write
rs
j
= f ront the relative state of ag
j
, because we have
f ront(s
i
, s
j
) = True. If ag
i
detects another agent k
on its left, we write rs = ( f ront, le f t). Figure 3 is an
example of such a joint relative state: the joint rel-
ative state for the middle agent is ( f ar − w; near −
sw; f ar − ne). The fourth neighbor is too far to be
observed, and thus is not a part of the interaction.
4.4.2 ΩR and OR: Observing Relative States
We described in sec. 4.3 how the individual compo-
nent is represented with a POMDP, so we have an ob-
COLLECTIVE DECISION UNDER PARTIAL OBSERVABILITY - A Dynamic Local Interaction Model
149

near,
south-west
far,
west
far,
north-east
out of sight
Figure 3: Example of a joint relative state.
servation set Ω and an observation function O used
for the individual states s
i
∈ S. Likewise, we have an
observation set ΩR and an observation function OR
used for the joint relative states. OR gives a proba-
bility to receive an observation o ∈ ΩR, once agents
acted and moved to a new joint state: it is used to es-
timate the relative state of each interacting agent. In
ISR, ΩR describes if a neighbor is observed, in which
direction (front, right, left, behind) and how far.
We have ΩR = {o
1
, . . . , o
|ΩR|
} a set of obser-
vations an agent can receive about its interacting
agents and OR : ΩR ×
S
m
i=0
SR
(i)
→ [0, 1] the joint
observation function. Here,
S
m
i=0
SR
(i)
is the set
of each possible joint relative state involving 0 to m
interacting agents. This joint observation function re-
turns a probability, according to an observation and a
transition to a new joint relative state.
4.4.3 C: Relation Clusters
In real world problems, it is often possible to extract
several sub-problems. If we consider a mobile robots
example and we add a door in the environment, then
we have two sub-problems: navigate in open spaces,
and cross doors. It is then possible to work on those
two problems independently, in order to break the
combinatorial complexity. Now, let us bring this idea
to our framework. In a given situation, interacting
agents are represented by a joint relative state. So, for
a given sub-problem, we have a set of joint relative
states. We call this set a relation cluster (RC).
In hSR, ΩR, OR,Ci, those RCs are represented by the
set C = {RC
1
, ..., RC
|C|
}. Those clusters are not com-
puted: it is an input of the problem like states, actions,
etc. We can see C as a representation of “how an agent
interacts with other agents”. This is an important as-
pect of this approach: for this reason, the next section
is dedicated to its formal description.
4.5 The “Relation Cluster” Concept
We can see a relation cluster as a situation, involving
an agent ag
i
interacting with other agents in a spe-
cific sub-problem associated to a set of joint relative
states. First, we give a formal definition. Second, we
explain how to choose those clusters, while designing
the problem description.
4.5.1 Definition
An agent i builds a cluster RC
n
= (S
n
, T
n
, R
n
) where
S
n
= {rs
1
, ..., rs
|S
n
|
} is a set of joint relative states
(such that ∀rs
j
∈ S
n
, rs
j
= (rs
j
1
, ..., rs
j
|rs
j
|
), with rs
j
k
∈
SR the relation describing how the agent k interacts
with the agent i), T
n
: S
n
× A × S
n
→ [0, 1] is a joint
transition function associated to the cluster n (with A
the same set of actions as in the individual problem)
and R
n
: S
n
× A × S
n
→ R is a joint reward function.
T
n
and R
n
are used to describe dependencies.
Each joint relative state can involve dependencies
over transitions, rewards or both. In DEC-POMDPs,
T and R are given for all joint states s ∈ S while in
our approach, they are only given for expressing de-
pendencies. In ISR, we could imagine that an agent
would not be able to cross a corridor if another agent
is already crossing it. So, if ag
i
is in a corridor and
considers that the joint relative state is (Front), we
have a dependency over transitions. But, if ag
1
con-
siders that the joint relative state is (Behind), we do
not have any dependencies, because ag
1
will be able
to cross the corridor without colliding with the other
agent. Still in this example, there are dependencies
over rewards for each joint relative state, because an
agent will receive a negative reward if it collides.
In order to compute a transition probability and a
reward for a given (rs, a, rs
0
), we will use T
n
if the
associated transition implies dependencies (and R
n
if
the reward implies dependencies). Otherwise, we will
use the individual functions T and R, coming from the
individual POMDP, to build the joint transitions and
rewards. Those joint functions only depend on the
action of ag
i
. More details are given in sec.5 about
how to build those functions.
4.5.2 How To Build Clusters
We described C as a set of k relation clusters RC
n
=
(S
n
, T
n
, R
n
). Those S
1
, . . . , S
k
are partitions of the set
of all possible joint relative states. With m the max-
imum number of interacting agents involved at the
same time, we have ∀rs ∈
S
m
i=0
SR
(i)
, ∃RC
j
|rs ∈ S
j
and ∀i, ∀ j, S
i
∩ S
j
=
/
0.
The goal is to split the set of joint relative states
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
150

into n clusters. First of all, we build an “empty” clus-
ter, associated to situations where agent i has no in-
teraction with any other agent. Such a cluster will be
RC = (
/
0,
/
0,
/
0), which means we have no joint relative
state, no joint transition and no joint reward. In such
a cluster, the agent can follow an individual and inde-
pendent policy with no need of coordination. The next
step consists in identifying sub-problems in order to
classify remaining joint relative states. Good clusters
will be such that there are many transitions between
the joint relative states of a given cluster, but only a
few transitions between two different clusters (weakly
coupled clusters and strongly coupled relative states
in the same cluster). In ISR, we could build a cluster
associated to the corridor crossing sub-problem, and
solve it as an independent problem without introduc-
ing too much approximations.
4.6 Sub-optimality of the Approach
Using this model, each agent will solve its own indi-
vidual problem, taking into account the existence of
the neighborhood. Such an approach is sub-optimal,
compared to standard approaches which compute op-
timal joint policies, but gave good results as shown in
our experiments (section 6.2). However, is it really
a good idea, to always seek the optimal joint policy?
It is proved that DEC-POMDPs are not approximable
(finding epsilon-approximations of the joint policy is
NEXP-hard (Rabinovich et al., 2003)). Then, could
not we just compute “good enough” policies, in order
to scale up to real world problems?
Our work is based on this idea, to quickly compute
a good policy, and avoid the huge amount of computa-
tion steps necessary to find the optimal one, while our
is good enough. Then, a difficult problem is to de-
termine if a policy is good enough. Our model gives
everything the agent needs to take its decisions: we
described not only how the agent evolves in its envi-
ronment and receives rewards, but also how the other
agents (the interacting ones) impact these rewards.
The next section introduces a set of algorithms, able
to compute a policy using this model.
5 ALGORITHMS
We developed two algorithms able to solve a problem
described with a DyLIM. First, we describe how to
find an upper bound for the combinatorial complex-
ity. Second, we give some details about how we build
the interaction problem. Third, we introduce our algo-
rithms solving the problems expressed with DyLIM.
5.1 Approximate Joint Relative States
The number of possible joint relative states grows ex-
ponentially with the number of involved agents: with
M the number of possible relations and I the number
of agents, we have (in the worst case) M
I
different
joint relative states (see §6.1 for a more detailed com-
plexity analysis). In order to bound this combinato-
rial explosion, we apply the same behavior as a hu-
man evolving in a crowd. In such a situation, the hu-
man only considers a subset of the people surround-
ing him. For example, he tries to avoid colliding with
people in front of him only.
We apply this idea in our algorithms with two as-
sumptions. First, we consider that one relation can
involve several agents. For example, if the agent
has three agents in front of it, and two on its left,
we consider that the induced joint relative state is
( f ront, le f t) and not ( f ront, f ront, f ront, . . . ). Sec-
ond, we have a preference order between rela-
tions and we consider a maximum of N relations
at the same time. For example, with N = 2 and
the order f ront > le f t > behind, the joint rela-
tive state ( f ront, behind, le f t) would be reduced to
( f ront, le f t). Because of those assumptions, we are
able to bound the combinatorial explosion at N (see
§6.1). If N is large enough, we compute good poli-
cies (for example, in a navigation problem, N = 4 is
enough to consider any immediate danger).
5.2 Building the Interaction Problem
The individual part of the problem is fully de-
scribed with the tuple hS, A, T, R, Ω, Oi, while the tu-
ple hSR, ΩR, OR,Ci used to describe the interaction
part needs a preliminary preprocessing before being
used. We already have the set of joint relative states
(S
1
, . . . , S
n
from each relation cluster RC
n
∈C) and the
observation function (ΩR and OR). In order to com-
pletely define the model, we define the joint transition
and reward functions, using C: we formalize each re-
lation cluster as a nearly independent MMDP.
5.2.1 Computing Transitions and Rewards
We consider an MMDP for each relation cluster
RC
n
= (S
n
, T
n
, R
n
) with S
MMDP
= S
n
and A
MMDP
=
A. For a given MMDP, we compute T(rs, a, rs
0
)
for each tuple (rs, a, rs
0
) using algorithm 1, the idea
for computing R(rs, a, rs
0
) being the same. In this
algorithm, we compute a transition between two
joint relative states, knowing that a joint relative
state rs = ( f ront, le f t) could be associated to the
joint state s
1
= ([x3, y0], [x3, y1], [x2, y0]), or s
2
=
([x2, y5], [x2, y6], [x1, y5]) etc. We call those joint
COLLECTIVE DECISION UNDER PARTIAL OBSERVABILITY - A Dynamic Local Interaction Model
151

Algorithm 1: Computing a transition.
Input: rs, a, rs
0
; RC
i
= (S
i
, T
i
, R
i
) a relation cluster
Result: the transition probability T(rs, a, rs
0
)
if T
i
(rs, a, rs
0
) is defined then return T
i
(rs, a, rs
0
)
T
i
(rs, a, rs
0
) ← 0;
foreach max(0, |rs −rs
0
|) ≤ out ≤ min(|rs|, I − |rs
0
|)
do
foreach subset G from rs with out agents do
foreach part rs” of rs
0
such that
|rs”| = |rs| − out do
// probability for the agents
of G to leave the
interaction:
p
out
←
∑
RC
j
6=RC
i
P
G
(RC
j
|RC
i
, a);
// probability for the |rs| − out
agents not in G to move to
the state rs”:
p
stay
← P
ag6∈G
(rs”|rs, a);
// probability for |rs
0
| − |rs”|
agents from the outside to
move to rs
0
− rs”:
p
in
← P
out
((rs
0
− rs”)|out, a);
// the global probability:
P
(G,s”)
(rs, a, rs
0
) ← p
out
× p
stay
× p
in
;
P
G
(rs, a, rs
0
) ←
∑
rs”
P
(G,rs”)
(rs, a, rs
0
);
T
i
(rs, a, rs
0
) ← T
i
(rs, a, rs
0
) +
∑
G
P
G
(rs, a, rs
0
);
return T
i
(rs, a, rs
0
);
states instances. We do not use all the instances
of rs but only a representative set. Indeed, a given
joint relative state can be associated to a lot of in-
stances, but it is not always interesting to use all of
them (most of the time, we only need to consider k of
the n available instances in order to compute transi-
tions and associated rewards, so we can avoid a lot of
useless computation steps).
This algorithm is based on rs and rs
0
the set of
interacting agents. Because of that, we suppose that
several agents could leave the interaction after mov-
ing from rs to rs
0
, and some others could join the in-
teraction. In the algorithm, p
out
, p
stay
and p
in
are used
to compute these probabilities:
• p
stay
, the probability for the agents not in G to
stay in interaction, can be an input of the problem
or computed from the POMDP. Its not an exact
probability (which would be impossible without
knowing the action taken by the other agents), but
a reachability for all the joint relative states,
• p
out
is the probability for the agents in G to move
to a state where they are not interacting anymore,
• p
in
is the probability, for k = |rs
0
| − |rs”| agents
not interacting with the agent, to move to the
joint relative state (rs
0
− rs”). This probability is
computed assuming a uniform distribution of the
I − |rs| remaining agents over unknown states.
Figure 4 is an example of such a transition.
1
2
3
4
1
2
3
4
A
B
1
2
3
4
1
2
3
4
Figure 4: Transition between two joint relative states.
In example A, the agent is interacting with 3 other
agents (top-let part of the figure). The agent moves
to the south, agents 2 and 3 do not move, agent 1
moves to the south-east and agent 4 moves to the
south. The bottom-left part of the figure is the result
of those moves: the joint relative state is now approx-
imately (top,left), agents 3 and 4 being too far to be
considered. Here, p
out
is the transition probability for
agent 3, p
stay
is the probability for agents 1 and 2 and
p
in
= 1 (no agent came from the outside of the interac-
tion). Probability for transition A is p
stay
× p
out
× p
in
.
In example B, the initial situation is the same (top-
right part of the figure), but agent 1 moves to the west
and agent 4 moves to the north-west. The result is
the same as example A, the joint relative state being
(top,left), but p
out
is now the probability for agents
1 and 3, p
stay
the probability for agent 2 and p
in
the
probability for agent 4. Then, the global transition
probability is the sum of examples A and B. We can
see, in this example, how a transition between two
joint relative state is computed as a sum of each possi-
ble case. We compute transition and reward functions
for each MMDP: we have to compute those functions
between two different MMDPs.
5.2.2 Transitions between Relation Clusters
To compute the transition probability from a re-
lation cluster to another one, we compute transi-
tions between their corresponding MMDPs (and the
associated rewards). So, for a given MMDP
i
=
hS
i
, A
i
, T
i
, R
i
i and for each MMDP
j
= hS
j
, A
j
, T
j
, R
j
i
with j 6= i, we apply algorithm 2.
In line 4 of this algorithm, we add an abstract state
j. Being in this state means “the agent is no longer
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
152

Algorithm 2: Transitions between two MMDPs.
Input: MMDP
i
, MMDP
j
Result: updated MMDP
i
// j=abstract state representing MMDP
j
:
S
i
← S
i
∪ { j};
A
i
← A
i
∪ A
POMDP
;
foreach rs ∈ S
i
and a ∈ A
i
(rs) do
// we compute T (rs, a, rs
0
) and R(rs, a, rs
0
)
with algorithm 1:
T
i
(rs, a, j) ←
∑
rs
0
∈S
j
T (rs, a, rs
0
);
r ←
∑
rs
0
∈S
j
[T (rs, a, rs
0
) × R(rs, a, rs
0
)]
∑
rs
0
∈S
j
T (rs, a, rs
0
)
;
R
i
(rs, a, j) ← r;
foreach rs ∈ S
i
and a ∈ A
POMDP
do
R( j, a, rs) ← 0;
if rs 6= j then T ( j, a, rs) ← 0;
else T ( j, a, rs) ← 1;
return MMDP
i
;
in the relation cluster i, but in the relation cluster j”.
Then we compute the associated transitions, between
j and each of the other states, describing how the
agent can move toward another MMDP. During the
solving process, we will change the value of this ab-
stract state, so it reflects the interest for the agent to
move toward the associated relation cluster.
5.3 The Solving Method
In this section, we present two methods to solve both
the individual and the interaction parts. Then, once
Pb
ind
and Pb
coo
are solved, we can give for each state
s a vector-value function V (s) = (V
ind
(s),V
coo
(s)).
5.3.1 Computing a Relational Belief State
We can easily compute a relational belief state b
r
over the set of joint relative states, like we do in a
POMDP. Such a belief state is needed in our two
methods. With S(rs) = {s ∈ S|∀rs
j
∈ rs, (s, −) ∈ rs
j
},
b
ind
(rs) =
∑
s∈S(rs)
b
ind
(s) and knowing a the action
taken by the agent, o the observation received about
the neighbors and b
ind
the belief state about the in-
dividual problem, the equation to update a relational
belief state b
r
t−1
to b
r
t
is the following: b
r
t
(rs
0
) =
OR(rs
0
, o)
∑
rs
b
ind
(rs) · b
r
t−1
(rs) · T
n
(rs, a, rs
0
)
∑
rs
00
OR(rs
00
, o)
∑
rs
b
ind
(rs) · b
r
t−1
(rs) · T
n
(rs, a, rs
00
)
5.3.2 POMDP+Q-MMDP
A first method consists in solving independently the
individual problem and the interaction one. We use
an existing POMDP solver, implementing the SAR-
SOP (Kurniawati et al., 2008) algorithm, to solve the
individual problem. Once this problem is solved, the
agent has a Q-value function Q
ind
(b
ind
, a) giving an
expected value for an action a in each possible indi-
vidual belief-state b
ind
about its states. We solve the
interaction problem with an algorithm inspired from
Value Iteration. This process is described in Algo-
rithm 3, with E the set of abstract states representing
a transition between two MMDPs.
Algorithm 3: Solving nearly independent MMDPs.
Input: M a set of MMDPs, ε a bound
E ← {abstract states};
foreach MMDP
i
∈ M and s ∈ S
i
do
if s ∈ E then V [i](s) ← 0 else V [i](s) ← R
i
(s);
repeat
// step 1 (doing Value Iteration):
foreach MMDP
i
∈ M do
V
0
[i] ← V I(MMDP
i
);
foreach s ∈ E do V
0
[i](s) ← 0;
// step 2 (propagating values):
foreach MMDP
i
∈ M do
foreach MMDP
j
∈ M such that j 6= i do
// E[i] representing MMDP
i
:
V
0
[ j](E[i]) ← max
s∈S
i
(V
0
[i](s));
// step 3 (computing values change):
∆ ← 0;
foreach MMDP
i
∈ M do
δ ← 0;
foreach s ∈ S
i
do
d ← |V [i](s) −V
0
[i](s)|;
if d > δ then δ ← d;
if δ > ∆ then ∆ ← δ;
V ← V
0
;
until ∆ < ε;
return V ;
Then we finally have, for each MMDP, a Q-Value
function Q
MMDP
(s, a) giving a value for each couple
(state,action). Moreover, those functions consider the
possibility to move from an MMDP to another, so the
agent can seek the best relation cluster according to
its current state. However, this function works in fully
observable settings, so we have to build a new func-
tion (using this one), working in partially observable
settings. With MMDP(s) the MMDP i such that s ∈
S
i
, we have Q
coo
(b
r
, a) =
∑
s∈b
r
b
r
(s).Q
MMDP(s)
(s, a).
However, such an approach implies the same
problems as those associated to Q-MDPs (see
COLLECTIVE DECISION UNDER PARTIAL OBSERVABILITY - A Dynamic Local Interaction Model
153

Figure 5: ISR. Figure 6: MIT. Figure 7: PENTAGON.
sec. 2.3), such as sub-optimality. During the prob-
lem execution, we keep a belief-state over individual
states, and another one over joint relative states. Us-
ing those beliefs, we can compute at each timestep an
individual value V
ind
and an interaction value V
coo
for
each action. Then, we choose the action offering the
best tradeoff between those two values. This method
gives good results on the benchmarks, but it could be
improved: the impact of the interaction over the indi-
vidual decisions is only computed at horizon 1.
5.3.3 Augmented-POMDP
In this second approach, we compute an Augmented-
POMDP hS
aug
, A
aug
, T
aug
, R
aug
, Ω
aug
, O
aug
i. We use
this augmented POMDP to describe the individual
problem of the agent augmented with informations
about the other agents. We write (1) S
aug
= S ×
(
S
|C|
i=0
S
i
), (2) Ω
aug
= Ω × ΩR and (3) A
aug
= A. The
transition function T
aug
((s, rs), a, (s
0
, rs
0
)) is given by
T (s, a, s
0
)×T
MMDP
(rs, a, rs
0
) (the observation and re-
ward functions O
aug
and R
aug
are defined in the same
way). T
aug
is the product of two independent func-
tions: we use this product because DyLIM constructs
the individual and the coordination problems as two
independent parts. Then, we solve this POMDP us-
ing SARSOP. This approach gives to the interactions
a long-term impact over the individual decisions. We
had nearly-optimal results using this method.
6 PERFORMANCES ANALYSIS
In this section, we analyze the performances of our
approach. First, we give the complexity of our algo-
rithms. Second, we give some experimental results,
solving a set of dedicated benchmarks.
6.1 Complexity of the Algorithms
There are two computation steps in our approach.
First, we compute the individual problem of the agent
and second, we solve this problem. The first step
implies computing k transitions and rewards: in the
worst case, all the agents are always interacting and
we have k = |S|
I
· |A| ·|S|
I
. Computing a transition (or
a reward) means computing p
out
, p
in
and p
stay
which
is done in O(X · I) with X the maximum number of
representative instance for a given joint relative state.
X can be fixed constant and low (sec. 5.2.1), so the
global complexity is in O(|S|
2I
· |A|· I). We described
in sec. 5.1 how the maximum number of relations
considered at the same time can be bound by N. Then,
with M = min(I, N), the complexity for the first step
is in O(|S|
2M
· |A| · M). This is exponential while the
number of agents is less than the bound N. With more
than N agents, the complexity stays constant. The sec-
ond step consists in solving the augmented POMDP
associated to the individual problem. The complexity
is known to be P-SPACE complete. If this augmented
POMDP is too large to be solved, then we apply the
POMDP+MMDP approach, solving a little POMDP
plus an MMDP (P complete).
6.2 Experimental Results
We chose, to evaluate our approach, to use a set of
problems recognized as dedicated benchmarks in the
community, coming from (Spaan and Melo, 2008).
6.2.1 Quality of the Behavior
We used instances of the problem described in
Sec. 4.2. In each of them (fig. 5 to 7), the state is de-
scribed by a couple (x, y) and a direction (N,S,E,W).
A reward of +10 is assigned when an agent reaches a
target, after what this agent can’t move anymore. If
two agents collide, a negative reward of -100 is as-
signed (the negative reward is not assigned one more
time if the agents stay collided, but only if they col-
lide again after separation). Each agent can move for-
ward, turn left or turn right with no cost, but each time
an agent moves forward it might derive with a proba-
bility of 0.05 for each side. Finally, an agent does not
know its position but receives observations about the
surrounding walls, and about its neighborhood: for
each direction (front, corner-front-right, right, corner-
right-behind, ...), the agent detects if there are neigh-
bors or not (we don’t know how many) and how far is
the closest. Our results are presented in table 1.
For each instance, we ran 1000 simulations (over
30 timesteps) and we solved each of them with indi-
viduals POMDPs (agents acting independently: lower
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
154

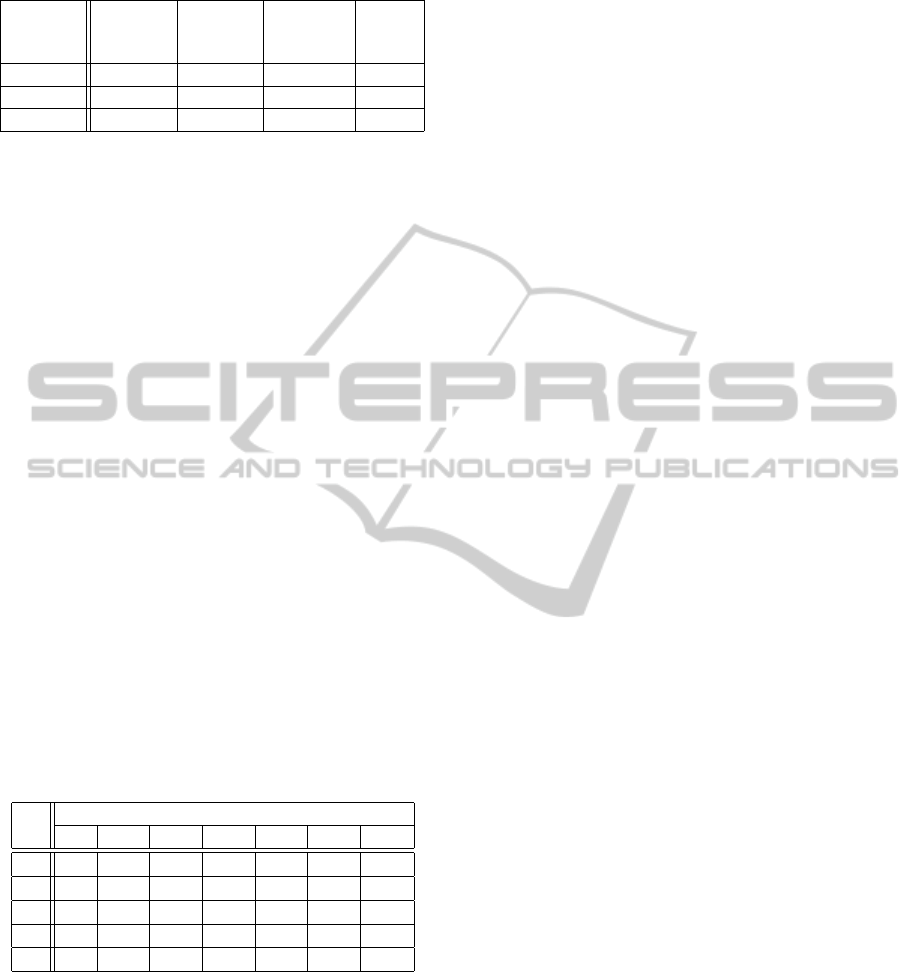
Table 1: Average Discounted Rewards (ADR).
Instance
Ind.
POMDPs
DyLIM
(POMDP
+MMDP)
DyLIM
(Augm.
POMDPs)
MMDP
ISR -14.8 8.49 11.28 12.84
MIT -14.5 9.18 11.57 12.96
PEN -14.94 8.39 10.72 13.11
bound), with our two algorithms and with the under-
lying MMDP (each agent is given a full observabil-
ity: optimal bound). With s
t
the joint state during the
timestep t, we computed these values using the equa-
tion: ADR =
∑
30
t=0
0.95
t
× R(s
t
).
Using our first algorithm (POMDP+MMDP),
we have average results (better than individual
POMDPs), but not satisfying enough: the agents man-
age to avoid collision, however once an agent is on a
target, the other agents stay near without moving to
the next target. Using the Augmented POMDP, the
agents have a long-term view of their interactions, so
they are able to reach each target. Then, we have
nearly-optimal results (in comparison to MMDP). In
each of those instances, the policy was computed in
less than 2 minutes (including the time needed to read
the input, compute the interaction problem, build the
Augmented-POMDP and solve it using SARSOP).
6.2.2 Scalability
We developed experiments about scalability, with
more than two agents and the results are very encour-
aging. Computation times for those experiments are
presented in table 2 (in each instance, the quality was
as good as in the previous examples).
Table 2: Computation times (’ = min., ” = sec., H = Hour).
N
I (number of agents)
2 3 4 5 6 7 100
1 3” 3” 3” 3” 3” 3” 3”
2 3” 27” 27” 27” 27” 27” 27”
3 3” 27” 7’ 7’ 7’ 7’ 7’
4 3” 27” 7’ 3H 3H 3H 3H
5 3” 27” 7’ 3H - - -
This table gives the computation times according
to the number of agents I and the bound N over the
number of interacting agents considered at the same
time. Intractable instances have a “-” value. We can
see that N efficiently bounds the computation time.
Moreover, we are able to compute policies with N =
4, which is a large enough bound for those instances.
7 CONCLUSIONS
This paper introduced DyLIM, a model used to
describe interaction-based DEC-POMDP-like prob-
lems, and two solving algorithms. This model al-
lows us to describe problems where an agent interacts
only sometimes, with a small set of agents, which is
a more realistic approach than classical models. Us-
ing this model, one can describe problems involv-
ing dynamic interactions (contrary to models such as
ND-POMDPs), without strong assumptions (contrary
to IDMG for example). We also described, using
our model and its structure, how to break the com-
binatorial complexity and compute good policies in
a bounded time. We were finally able to scale up to
large problems, involving up to 100 agents.
REFERENCES
Bernstein, D., Zilberstein, S., and Immerman, N. (2000).
The complexity of decentralized control of markov
decision processes. In Proc. of UAI.
Boutilier, C. (1996). Planning, learning and coordination in
multiagent decision processes. In TARK.
Cassandra, A., Kaelbling, L., and Littman, M. (1994). Act-
ing optimally in partially observable stochastic do-
mains. In Proc. of AAAI.
Kumar, A. and Zilberstein, S. (2009). Constraint-based dy-
namic programming for decentralized POMDPs with
structured interactions. In Proc. of AAMAS.
Kurniawati, H., Hsu, D., and Lee, W. (2008). SARSOP:
Efficient point-based POMDP planning by approxi-
mating optimally reachable belief spaces. In Proc.
Robotics: Science and Systems.
Littman, M., Cassandra, A., and Pack Kaelbling, L. (1995).
Learning policies for partially observable environ-
ments: Scaling up. In Machine Learning, pages 362–
370.
Nair, R., Varakantham, P., Tambe, M., and Yokoo, M.
(2005). Networked distributed pomdps: A synthesis
of distributed constraint optimization and pomdps. In
Proc. of AAAI.
Oliehoek, F., Spaan, M., Whiteson, S., and Vlassis, N.
(2008). Exploiting locality of interaction in factored
Dec-POMDPs. In Proc. of AAMAS.
Rabinovich, Z., Goldman, C., and Rosenschein, J. (2003).
The complexity of multiagent systems: The price of
silence. In Proc. of AAMAS.
Shapley, L. (1953). Stochastic games. In National Academy
of Sciences.
Spaan, M. and Melo, F. (2008). Interaction-driven Markov
games for decentralized multiagent planning under
uncertainty. In Proc. of AAMAS.
Varakantham, P., Kwak, J., Taylor, M., Marecki, J., Scerri,
P., and Tambe, M. (2009). Exploiting coordination
locales in distributed POMDPs via social model shap-
ing. In Proc. of ICAPS.
COLLECTIVE DECISION UNDER PARTIAL OBSERVABILITY - A Dynamic Local Interaction Model
155