GENETIC SOLUTIONS TO MIXED H
2
/H
∞
PROBLEMS
Limits of Performance
Gustavo S´anchez, Miguel Strefezza
Universidad Sim´on Bol´ıvar, Departamento de Procesos y Sistemas, Caracas, Venezuela
Minaya Villasana
Universidad Sim´on Bolivar, Departamento de C´omputo Cient´ıfico, Caracas, Venezuela
Keywords:
Multi-objective control, Genetic algorithms, LMIs, Pole placement, COMPl
e
ib.
Abstract:
One of the most relevant problems for control engineers is the so-called “mixed H
2
/H
∞
”. To solve it, different
convexifying strategies became popular in the later 1990s, mainly based on Linear Matrix Inequalities (LMIs).
On the other hand, genetic algorithms have also been applied for H
2
/H
∞
synthesis. Indeed, several authors
agree that they are able to find good solutions to this important control problem. However, in most of the
published papers, only low-order SISO models have been considered. In the present paper a LMI-based
algorithm is compared against a genetic algorithm, with respect to three performance indicators: Set Coverage,
Maximum Distance and Efficient Set Spacing. Five open-loop MIMO models extracted from COMPl
e
ib are
studied, for which the degree varies between 5 and 10. Based on numerical results, the genetic algorithm is
not able to improve LMI solutions for problems with more than 42 variables, restricted to a budget of 20.000
function evaluations.
1 INTRODUCTION
One of the most important problems for control engi-
neers is the so-called “mixed H
2
/H
∞
”. Typically, the
H
∞
channel is used to enhance the robustness of the
closed-loop system, whereas the H
2
channel guaran-
tees good performance (Apkarian et al., 2008).
To solve this problem, different convexifyng
strategies became popular in the later 1990s, despite
the inherent conservatism of this approach. For
instance, in (Scherer et al., 1997) controllers are
designed by solving a set of LMIs in tandem with
nonlinear algebraic equalities. In fact, this design
method (enhanced with many improvements over the
years) remains as state of the art for this problem.
On the other hand, Multi-Objective Evolutionary
Algorithms (MOEA) have also been applied for
H
2
/H
∞
synthesis: in (Takahashi et al., 2001) and
(Takahashi et al., 2004), a genetic approach is pro-
posed to obtain H
2
/H
∞
solutions which are consis-
tent with a Pareto set and less conservative compared
to LMI solutions.
After these examples it may seen obvious that, un-
der special circumstances, genetic algorithms are in
fact able to find better solutions than LMI-based al-
gorithms. However, in most of the published works
which have been consulted for this paper, only low-
order and SISO models have been considered, more
appropriate to evaluate low-complexity controllers as
PIDs (Astrom et al., 1998).
In this manner, the question arises as to whether
the genetic algorithm advantage remains true when
the open-loop models are high-order and MIMO
(Multiple Input Multiple Output) as those proposed
in COMPl
e
ib (Leibfritz, 2004).
The rest of this paper is organized as follows. In
section 2, the controller design problem is formulated.
Next, the two design methods to be compared are
described in section 3. In section 4, numerical results
are presented and conclusions are given in section 5.
2 PROBLEM FORMULATION
The closed-loop system is shown in figure 1. Matri-
ces A ∈ R
n×n
, B ∈ R
n×n
u
and C ∈ R
n
y
×n
denote the
corresponding open-loop state matrices.
The open-loop state-space equations are:
282
Sánchez G., Strefezza M. and Villasana M..
GENETIC SOLUTIONS TO MIXED H2/H∞ PROBLEMS - Limits of Performance.
DOI: 10.5220/0003640702820285
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 282-285
ISBN: 978-989-8425-83-6
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

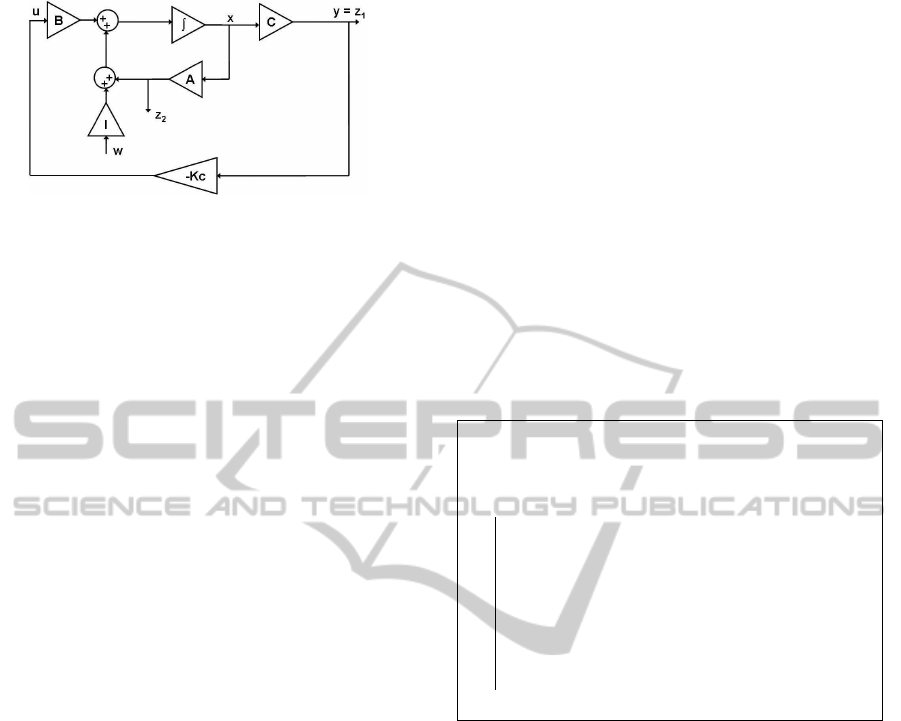
Figure 1: Continuous-time closed-loop design model.



˙x = Ax+ Iw+ Bu
z
1
= y = Cx
z
2
= Ax
(1)
In this formulation, w ∈ L
n
w
×1
2
denotes the exoge-
nous input, z
1
∈ L
n
z
1
×1
2
and z
2
∈ L
n
z
2
×1
2
represents the
outputs to be regulated, while u ∈ L
n
u
×1
2
and y ∈ L
n
y
×1
2
represent the control input and the measured out-
put respectively. It is assumed the open-loop model
is strictly proper, stabilizable from u and detectable
from y.
Consider a full-order linear controller K
c
described by the state equations
K
c
:

˙x
c
= A
K
x
c
+ B
K
y
u = C
K
x
c
+ D
K
y
(2)
Finally, let
G
1
(K
c
) = G
z
1
w
(K
c
)
G
2
(K
c
) = G
z
2
w
(K
c
) (3)
be the closed-loop transfer function from w to z
1
and
z
2
respectively. The mixed H
2
/H
∞
control problem is
stated as:
P
H
2
/H
∞
: min
K
c

kG
1
(K
c
)k
2
kG
2
(K
c
)k
∞

subject to
G
1
(K
c
) and G
2
(K
c
) are stable
(4)
In this formulation the term min should be interpreted
as the search for the best possible approximation of
the corresponding Pareto-optimal set.
3 DESIGN METHODS
In this section two methods to solve the multi-
objective problem P
H
2
/H
∞
are described.
3.1 LMI-based Method
In this sub-section a design algorithm based on the re-
sults presented in (Scherer et al., 1997) is proposed.
In fact, these authors demonstrated that given two
positive scalars γ
2
,γ
∞
the following equations hold
kG
1
(K
c
)k
2
≤ γ
2
(5)
kG
2
(K
c
)k
∞
≤ γ
∞
if there exist matrices X > 0,Y > 0,
b
A,
b
B,
b
C,
b
D such
that a certain set of LMIs are feasible.
To build the approximation of the Pareto-front,
the following iterative procedure is proposed (see
Algorithm 1): First the limit of one restriction is
increased and the other one decreased (i.e. linearly).
Then, the feasability problem is solved and the solu-
tion K
c
is archived, only in case it is non-dominated.
Otherwise it is rejected.
Algorithm 1: Algorithm to solve P
H
2
/H
∞
via LMIs.
Data: G
1
,G
2
,N
H
2
/H
∞
,∆γ
2
,∆γ
∞
,γ
min
,γ
max
Result: P
k = 1;
while k ≤ N
H
2
/H
∞
do
Solve



G
2
(K
k
c
)



2
≤ γ
min
+ k∆γ
2



G
1
(K
k
c
)



∞
≤ γ
max
− k∆γ
∞
P
k
= U pdateArchive(K
k
c
,P
k−1
);
k = k + 1;
end
3.2 Multi-objective Pole Placement with
Evolutionary Algorithms
(MOPPEA)
In the following we describe a design method, named
Multi-Objective Pole Placement with Evolutionary
Algorithms (MOPPEA).
In the general case, an output feedback controller
can be designed by combining a full information con-
troller with a state observer. The resulting output
feedback sub-system is called “observer-based con-
troller” and has the following state-equations:

·
x
c
= (A + BK + LC)x
c
− Ly
u = Kx
c
(6)
where x
c
is the estimated state.
Let pk ∈ C
n
k
and pl ∈ C
n
l
be the eigenvalues of
A + BK and A + LC respectively. To assure closed-
loop system stability, the gain matrix K and L must be
calculated in such way that pk and pl belong to C
−
(open left-half complex plan).
GENETIC SOLUTIONS TO MIXED H2/H8 PROBLEMS - Limits of Performance
283

Thus, the key concept of the proposed design
method is using an evolutionary process in order to
evolve matrices K ∈ R
n
u
×n
and L ∈ R
n×n
y
. Thus, the
mixed H
2
/H
∞
control problem is stated again as:
b
P
H
2
/H
∞
: min
K∈R
n
u
×n
,L∈R
n×n
y

kG
1
(K,L)k
2
kG
2
(K,L)k
∞

subject to
G
1
(K,L) , G
2
(K,L) are stable
(7)
Regarding the initial population, it can be
generated using the algorithm proposed in (S´anchez
et al., 2007). After that, SPEA2 is used to drive
the design process, taking advantage of its ability to
manage an archive of non-dominated solutions.
4 NUMERICAL RESULTS
In this section two algorithms are compared:
A1: SPEA2 - enhanced with special operators and
restricted to 20.000 objective function evalua-
tions, using the parameters shown in table 1.
This quantity was fixed considering the total time
available for computations.
A2: LMI-based design (see Algorithm 1).
Table 1: Setting parameters used for SPEA2.
Parameter Value
Initial Population Randomly generated
Representation K + L
Cross-Over Recombination Arithmetical
Cross-Over Rate 0.9
Mutation Operator Gaussian
Mutation Rate 0.1
Population Size 200
Stop Condition 100 generations
Population Size 100
Offspring Size 100
Table 2 (at the top of the next page) presents
the information related with the selected COMPl
e
ib
models, each one characterized by a particular
nomenclature. Five models were selected: AC1, AC6,
WEC1, NN10 and AC9, for which the number of
decision varies between 30 and 90. Table 2 also
presents, for each model, the parameters N
H
2
/H
∞
,∆γ
2
,
∆γ
∞
, γ
min
and γ
max
used by A2.
Thirty executions were simulated for each algo-
rithm and for each problem. Let P F
1
and P F
2
be
the Pareto approximations found by two different al-
gorithms. To compare their performance, the follow-
ing indicators were computed:
• Set Coverage(C)
• Maximum Distance(MD)
• Efficient Set Spacing(ESS)
The values obtained for these indicators are shown
in tables 3 and 4. For each indicator the mean value
and the standard deviation within parentheses are pre-
sented. These results confirm that the LMI-based
algorithm is able to produce dominating solutions
with respect to the genetic algorithm, for problems
with more than 42 decision variables. Note that A1
achieves better results than A2 with respect to MD.
However, A2 achieves better results with respect to
ESS, which can be explained given the deterministic
nature of A1.
Table 3: Set coverage results.
C(A
i
,A
j
) A1 A2
A1 −
AC1:0.8619(0.1326)
AC6:0(0)
NN10:0(0)
WEC1:0(0)
AC9:0(0)
A2
AC1:0(0)
AC6:0(0)
NN10:1(0)
WEC1:1(0)
AC9:1(0)
−
Table 4: MD and ESS results.
MD ESS
A1
AC1:0.7589(0.0535)
AC6:120.4263(67.0600)
NN10:3.5940(0.7046)
WEC1:45.3320(7.7541)
AC9:564.2026(190.4456)
AC1:0.0190(0.0069)
AC6:3.5698(4.0164)
NN10:0.1026(0.0407)
WEC1:1.0784(0.4881)
AC9:21.5037(17.8440)
A2
AC1:0.1618(0)
AC6:2.8065(0)
NN10:1.0200(0)
WEC1:36.0976(0)
AC9:59.2017(0)
AC1:0.0122(0)
AC6:0.0152(0)
NN10:0.0188(0)
WEC1:0.1540(0)
AC9:3.3800(0)
5 CONCLUSIONS
In this paper, we analyze the performance of a genetic
algorithm (SPEA2) to solvefive mixed H
2
/H
∞
design
problems, taking as reference a LMI-based iterative
algorithm and considering a fixed budget of 20.000
evaluations.
Based on the obtained results, the following con-
clusions can be stated:
• Unlike other representations, the proposed (K,L)
chromosome is able to efficiently explore the con-
troller space, even for models with order greater
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
284

Table 2: Information related with the selected COMPl
e
ib models.
COMPl
e
ib n n
u
n
y
n
MOPPEA
N
H
2
/H
∞
∆γ
2
∆γ
∞
γ
min
γ
max
r
max
i
max
AC1 5 3 3 30 100 0.01 0.01 1.5 5.5 10 10
AC6 7 2 4 42 100 0.1 1 1 110 20 20
NN10 8 3 3 48 100 0.01 0.02 3 15 10 10
WEC1 10 3 4 70 100 0.05 1 2 200 100 100
AC9 10 4 5 90 100 0.1 0.1 50 100 100 100
than 4 and with multiple inputs and outputs. The
proposed variation operators allows to stay within
the feasible region.
• The statistical tests show the genetic algorithm is
not able to improve LMI solutions for problems
with more than 42 variables, considering a fixed
budget of 20.000 function evaluations.
As future work, more simulations need to be
carried out, to find how many function evaluations
are to be allowed in order the genetic algorithm is
competitive again. It is also possible to test ”hy-
brid” design methods, based on both deterministic
and stochastic strategies to find better Pareto approxi-
mations.
REFERENCES
Apkarian, P., Noll, D., and Rondepierre, A. (2008). Mixed
H
2
/H
∞
control via nonsmooth optimization. SIAM
Journal on Control and Optimization, 47(3):1516–
1546.
Astrom, K., Panagopoulos, H., and Hagglund, T. (1998).
Design of PI controllers based on non-convex opti-
mization. Automatica, 34(5):585–601.
Leibfritz, F. (2004). COMPlib - Constrained Matrix-
optimization Problem Library. Technical report, Uni-
versity of Trier. Department of Mathematics, Ger-
many.
S´anchez, G., Villasana, M., and Strefezza, M. (2007).
Multi-Objective Pole Placement with Evolutionary
Algorithms. Springer-Verlag. Berlin. Series: Lecture
Notes in Computer Science, 4403:417–427.
Scherer, C., Gahinet, P., and Chilali, M. (1997). Multi-
objective output-feedback control via LMI optimiza-
tion. IEEE Transactions on Automatic Control,
42(7):896–910.
Takahashi, R., Palhares, R., Dutra, D., and Goncalves,
L. (2001). Synthesis and characterization of Pareto-
optimal solutions for the mixed H2/Hinf problem.
Proceedings of the 40th IEEE conference on decision
and control. Orlando,FL. USA, pages 3997–4002.
Takahashi, R., Palhares, R., Dutra, D., and Goncalves, L.
(2004). Estimation of Pareto sets in the mixed H
2
/H
∞
control problem. International Journal of System Sci-
ence, 35(1):55–67.
GENETIC SOLUTIONS TO MIXED H2/H8 PROBLEMS - Limits of Performance
285