
A FAST ALGORITHM FOR MINING GRAPHS OF PRESCRIBED
CONNECTIVITY
Natalia Vanetik
Deutsche Telecom Laboratories and CS department, Ben Gurion University, Beer Sheva, Israel
Keywords:
Mining graphs, Graph connectivity.
Abstract:
Many real-life data sets, such as social and biological networks and biochemical data, are naturally and easily
modeled as large labeled graphs. Finding patterns of interest in these graphs is an important task, due to
the nature of the data not all of the patterns need to be taken into account. Intuitively, if a pattern has high
connectivity, it implies that there is a strong connection between data items. In this paper, we present a novel
algorithm for finding frequent graph patterns with prescribed connectivity in large single-graph data sets.
We employ the Dinitz-Karzanov-Lomonosov cactus minimum cut structure of a graph to perform the task
efficiently. We also prove that the suggested algorithm generates no more candidate graphs than any other
algorithm whose graph extension procedure we use at the first step.
1 INTRODUCTION
Representing large complex naturally occurring data
structures as labeled graphs has gained popularity in
the last decade due to the simplicity of the translation
process and because such a representation is intuitive
to users. The graph is now a standard format for rep-
resenting social and biological networks, biochemi-
cal and genetic data, and Web and document struc-
ture. Frequent subgraphs that represent substructures
of the dataset, which are characteristic to that dataset,
are considered important and useful indicator of the
nature of the dataset. Frequent subgraphs are used to
build indices for graph datasets (Zhang,Li,Yang2009)
that improve search efficiency, to facilitate classifi-
cation or clustering for machine learning tasks (See-
land,Girschick,Buchwald,Kramer 2010), and to de-
termine normal and abnormal structures within the
data (Horv´ath,Ramon 2010).
Not all of the frequent subgraphs are usually of
interest to the user performing a specific search task,
both because of the subgraph meaning in the particu-
lar database and because of the high complexity of the
graph mining problem. This obstacle becomes espe-
cially disturbing when the dataset in question is rep-
resented by a single very large labeled graph, such
as a Web or a DNA sequence. In this paper, we
concentrate on the problem of finding frequent sub-
graphs that satisfy a user-defined constraint of mini-
mum edge connectivity, that determines how many e-
dges should be removed from a graph in order to
separate it into two parts. A minimal edge connectiv-
ity requirement allows us to discard frequent graphs
that do not characterize strong relations between
data items in the native dataset. Moreover, the edge
connectivity of a graph can be verified fairly easily
(in polynomial time and space), unlike some of the
other constraints, such as symmetry, maximum clique
size etc.
While there is a number of algorithms for the
task of general frequent subgraph mining exist
(see, for instance (Kuramochi,Karypis 2001)), the
issue of finding frequent graphs that are subject to
connectivity constraints has rarely been addressed in
the literature. In (Yan,Zhou,Han 2005), the authors
address the issue of mining all closed frequent graphs
with predefined edge connectivity and propose two
algorithms that handle this problem. The algorithms
do not address the issue of frequent patterns that have
high connectivity but are not closed.
The authors of (Papadopou-
los,Lyritsis,Manolopoulos 2008) have proposed
the ‘CODENSE’ algorithm that finds coherent dense
subgraphs – all edges in a coherent subgraph exhibit
correlated occurrences in the whole graph set; these
graphs naturally have high connectivity.
In this paper, we propose a novel graph mining
algorithm that finds frequent subgraphs with a
user-specified constraint on edge connectivity. Our
algorithm uses the minimum cut structure of a graph
5
Vanetik N..
A FAST ALGORITHM FOR MINING GRAPHS OF PRESCRIBED CONNECTIVITY.
DOI: 10.5220/0003628300050013
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 5-13
ISBN: 978-989-8425-79-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

in order to perform the task efficiently; this structure
can be computed in low polynomial time (even linear,
if one uses the randomized algorithm of (Karger, Pan-
igrahi 2009)), which makes our algorithm especially
suitable for databases consisting of a single large
graph. The mincut structure of a graph also allows
us to increase frequent patterns by more than just a
node or an edge at a time than the standard approach.
We also prove the optimality of this algorithm by
showing that every frequent subgraph produced by
our algorithm (even if it is only used as a building
block for a supergraph satisfying edge connectivity
constraints) has to be produced by a competing
algorithm.
This paper is organized as follows. Section 2 con-
tains the basic definitions and graph theoretic facts
required for our approach. Section 3 describes the
algorithm and contains proofs of the algorithm’s cor-
rectness. Section 4 contains the proof of algorithm’s
optimality.
2 STATEMENT OF THE
PROBLEM
2.1 Basic Definitions
In this paper, we deal with undirected labeled graphs.
In a graph G = (V, E), V denotes the node set, E ⊆
V ×V denotes the edge set, and each node v ∈ V has a
label l(v). A graph G
′
= (V
′
,E
′
) is called a subgraph
of G, denoted by G
′
⊆ G, if V
′
⊆ V, E
′
⊆ E and ev-
ery edge in E
′
has both ends in V
′
. G
′
is an induced
subgraph of G if it is a subgraph of G and for every
pair of nodes v,u ∈ V
′
such that (u,v) is an edge of G,
(u,v) is also an edge of G
′
.
A graph G = (V, E) is disconnected if there exists
a partitionV
1
,V
2
ofV so that no edge in E has one end
in V
1
and another in V
2
. If no such partition exists,
G is called connected. G is called k-edge-connected,
k ∈ N, if G is connected and one has to remove at least
k edges from E to make G disconnected.
A partition of edge set E into X ⊂ E and X :=
E \ X is called a cut. Removing all edges having one
end in X and another in X (called (X, X)-edges) from
G disconnects the graph. The size of a cut (X,X) is
the number of (X,X)-edges, denoted |(X,X)|. The
(X,X)-edges whose removal disconnects the graph
are often also called a cut. A cut of minimum size
is called a minimum cut or a mincut. The smallest
size of a cut in a graph is the edge connectivity of a
graph. In general, for two foreign subsets X,Y ⊂ V
we denote by |(X,Y)| the number of edges in G with
one end in X and another in Y.
We study the problem of graph mining in the fol-
lowing setting: our database is a single large undi-
rected labeled graph G. We are given a user-supplied
support threshold S ∈ N and a connectivity constraint
k and we are looking for all k-edge-connected sub-
graphs of G with a count of at least S (these sub-
graphs are called frequent). The count of a graph
in a database is determined by a function count()
that satisfies the downward closure property: for all
subgraphs g
1
,g
2
of any database graph D such that
g
1
⊆ g
2
we always have count(g
1
,D) ≥ count(g
2
,D).
The main idea of our approach is to employ the spe-
cial structure of mincuts in the database graph in or-
der to make the search for frequent k-edge-connected
subgraphs faster.
2.2 The Cactus Structure of Mincuts
An unweighted undirected multigraph is called a cac-
tus if each edge is contained in exactly one cycle
(i.e., any pair of cycles has at most one node in com-
mon). Dinitz, Karzanov and Lomonosov showed in
(Dinits,Karzanov,Lomonosov1976) that all minimum
cuts in a given graph with n vertices can be repre-
sented as a cactus of size 0(n). This cactus represen-
tation plays an important role in solving many con-
nectivity problems, and we use it here for the efficient
mining of graphs with connectivity constraints.
Formally, let G = (V,E) be an undirected multi-
graph and let {V
1
,...,V
n
} be a partition of V. We de-
note the set of all minimum cuts of G by Cuts(G) .
Let R = (V
R
,E
R
) be a multigraph with node set V
R
:=
{V
1
,...,V
n
} and edge set E
R
:= {(V
i
,V
j
) | (v
i
,v
j
) ∈
E, v
i
∈ V
i
,v
j
∈ V
j
}.
Definition 1. R is a cactus representation of Cuts(G)
if there exists a one-to-one correspondence ρ :
Cuts(G) → Cuts(R) such that for every mincut
(X,X) ∈ Cuts(G) ρ((X,X)) ∈ Cuts(R) and for every
mincut (X, X) ∈ Cuts(R) ρ
−1
((X,X)) ∈ Cuts(G).
Dinitz, Karzanov and Lomonosov
(Dinits,Karzanov,Lomonosov 1976) have proved
that for any undirected multigraph, there exists a
cactus representation (in fact, they showed that this
is always true for any weighted multigraph). A dual
graph to any cactus representation, if the cactus
cycles are taken as nodes, is a tree. The size of a
cactus tree is linear in the number of vertices in the
original graph, and any cut can be retrieved from the
cactus representation in time linearly proportional to
the size of the cut. In addition, the cactus displays
explicitly all nesting and intersection relations among
minimum cuts. Note that a graph can have at most
n
2
mincuts, where n is the size of graph’s node
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
6

set. The following definition and a fundamental
lemma entirely describe the structure of a cactus
representation.
Definition 2. Let λ be the size of a mincut in graph
G = (V,E). A circular partition is a partition of V
into k ≥ 3 disjoint subsets {V
1
,...,V
k
} such that
1. |(V
i
,V
j
)| = λ/2 when j − i = 1 mod k.
2. |(V
i
,V
j
)| = 0 when j − i 6= 1 mod k.
3. For 1 ≤ a < b ≤ k, ∪
b−1
i=a
V
i
is a mincut. Moreover,
if any mincut (X, X) is not of this form, then either
X or X is contained in some V
i
.
Lemma 1. (Dinits,Karzanov,Lomonosov1976; Bixby
1974) If X
1
and X
2
are crossing cuts in G (have a
non-trivial intersection as sets), then G has a circu-
lar partition {V
1
,...,V
k
} such that each of X
1
∩ X
2
,
X
1
∪ X
2
, X
1
\ X
2
and X
2
\ X
1
equal ∪
b−1
i=a
V
i
for appro-
priate choices of a and b.
Corollary 1. (Dinits,Karzanov,Lomonosov1976) Ev-
ery graph has a cactus representation.
Corollary 2. (Fleischer 1998) Every graph on n ver-
tices has a cactus representation with no more than
2n− 2 vertices.
Figure 1 shows a 2-edge-connected multigraph
and its cactus representing all three mincuts that exist
in the graph. In this example, there is a one-to-one
correspondence between the cycles of the cactus and
the circular partitions of G.
2.3 Cactus Construction Algorithms
The earliest well-defined algorithm for finding all
minimum cuts in a graph uses maximum flows
to compute mincuts for all pairs of vertices (see
(Gomory,Hu 1991)). Karzanov and Timofeev
(Karzanov,Timofeev 1986) outlined the first algo-
rithm to build a cactus for an unweighted graph. A
randomized algorithm by Karger (Karger,Stein 1996)
finds all minimum cuts in O(n
2
logn) time. Fleis-
cher in (Fleischer 1998) describes an algorithm that
arranges the minimum cuts into an order suitable for
a cactus algorithm which runs in O(nm + n
2
logn)
time. Finally, Karger and Panigrahi proposed a near-
linear time randomized algorithm in (Karger, Pani-
grahi 2009).
3 FINDING FREQUENT
K-CONNECTED GRAPHS
In this section, we present the CactusMining algo-
rithm for finding all frequent k-connected graphs in
a graph database. For simplicity, we assume here that
the database is a single large graph; when a database
consists of two or more disconnected graphs, graph
decomposition and support counting should be per-
formed once for each transaction. The CactusMining
algorithm searches for all frequent k-connected sub-
graphs in a bottom-up fashion and relies on the search
space reduction that is implied by the cactus structure
of the database.
3.1 Computing the Cactus Structure of
a Graph
To compute the cactus structure for a given graph
G and a connectivity bound k, we employ a cactus-
constructing algorithm, denoted as BuildCactus()
(for instance, the one described in (Fleischer 1998)).
3.2 Basic Properties
In this section, we describe several useful properties
of a cactus mincut structure.
Property 1. Let g be a (k+1)-connected subgraph of
G. Then g is entirely contained in some V
i
, 1 ≤ i ≤ k.
The converse is not true, i.e. non-k-edge-connected
subgraphs of V
i
may exist.
Property 2. Let g be a k-edge-connected subgraph
of G. Let C be a minimal subcactus of G with circu-
lar partition {V
1
,...,V
k
} containing g as a subgraph.
Then either g contains all the (V
i
,V
j
)-edges or it con-
tains no such edges.
Proof. This property is trivial since removing a
(V
i
,V
j
)-edge decreases the edge connectivity of a sub-
cactus C containing g.
Corollary 3. In Property 2, subgraph g∩V
i
contains
all the nodes incident to the (V
i
,V
j
)-edges of a circu-
lar partition.
Proof. Follows from the fact that g contains all
(V
i
,V
j
)-edges.
3.3 Growing Subgraphs
In this section, we describe how an instance of a can-
didate subgraph can be grown from an existing fre-
quent subgraph instance without violating connectiv-
ity constraints.
The intuition behind our subgraph extension ap-
proach relies on properties of its location within the
cactus structure. Let T = (V
T
,E
T
) be a dual cactus
structure of (k + 1)-cuts in database D with nodes
V
T
being the cactus cycles and the adjacency rela-
tion E
T
determining whether two cactus cycles share
A FAST ALGORITHM FOR MINING GRAPHS OF PRESCRIBED CONNECTIVITY
7

C
1
C
3
C
2
C
3
C
1
C
3
a mincut
a mincut
(a) Graph G with mincut size = 2 (b) A corresponding cactus structure of G.
Figure 1: A cactus structure of a graph.
a node. Each cactus cycle C ∈ V
T
is a graph, denoted
by C = (V
C
,E
C
), with the structure of a simple cycle.
In C, the nodes of V
C
are the basic (k + 1)-connected
components of D, i.e. the components that contain no
edge of a k-cut in D. Two such componentsc
1
,c
2
∈V
C
are adjacent if there exist edges of D that belong to a
k-cut and are incident to nodes in c
1
and c
2
(there are
precisely ⌈
k
2
⌉ such edges). To simplify the notation,
we say that (c
1
,c
2
) denotes the set of these edges.
Our goal is to extend instances of frequent graphs
gradually, while complying with the following rule:
• do not produce an extension whose cactus struc-
ture in C does not ensure k-connectivity.
In order to achieve the objective, our extension pro-
cedure depends strongly of the location of an instance
within the database cactus structure. Moreover, our
approach allows to extend an instance by more than
one node.
Let f ⊂ D be a frequent subgraph instance that we
are currently extending. We introduce several addi-
tional parameters of f that are updated by our mining
algorithm:
1. f.type can assume the values node, cycle and
tree,
2. f.cycle denotes the node t ∈ V
T
containing f as a
subgraph (if one exists),
3. f.tree denotes the subtree of T containing f as a
subgraph; | f.tree| denotes the number of nodes in
the said subtree.
For each value of f.type, we propose a separate exten-
sion procedure. The first two procedures extend the
subgraph instance within its own type; they can fail
to extend either because no extension is possible at all
or because the type of extension needs to be changed.
For f.type = cycle and f.type = tree, additional pre-
caution needs to be taken in order to ensure a better
search space reduction. In this case, a subgraph of
such an instance contained within a (k+ 1)-connected
Algorithm 1: Contraction().
Input: subgraph g,
subcactus T containing g.
Output: contraction of g
1: K := a node of T containing g;
2: for all subtrees t ∈ T incident to K do
3: replace t \ {g, cycle edges incident to g}
with a single node;
4: end for
5: return T;
component of the database graph may cause a cut of
size less than k to appear in the extended instance. We
apply the Contraction() procedure (see Section 3.3.1)
that determines exactly if these subgraphs produce a
smaller than required edge cut or not.
3.3.1 The Contraction Procedure
The Contraction() procedure, described in Algorithm
1, receives as an input a subgraph g contained in a
(k + 1)-connectivity component of a cactus structure
T, and contracts all the parts of T that are not adjacent
or incident to g into single nodes. For each subtree
t ∈ T adjacent to g, t \ g is turned into a single node.
In fact, every such subtree is turned into a two-node
cycle with t and t \ g as nodes, and the cycle edges
incident to g as edges.
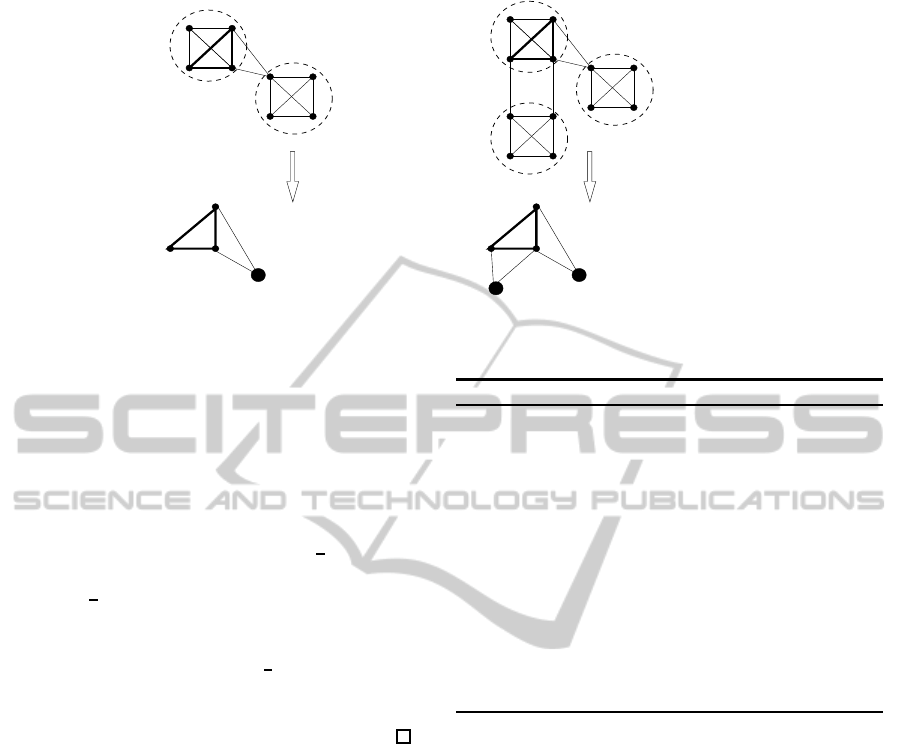
Figure 2 gives two examples of applying the Con-
traction() procedure.
The following claim ensures correctness of the
procedure.
Claim 1. Let T = (V
T
,E
T
) be a cactus structure of
k-cuts in a graph G and let a subgraph f ⊂ G span
the (k+ 1)-connectivity components of T and contain
all the cycle edges of the cactus structure. Then there
exists a (k + 1)-connectivity component K of G such
that Contraction( f ∩ K,T) is not k-connected if and
only if f is not k-connected.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
8
g
T is a treeT is a single cycle
g
cycle edges
g
cycle edges
a contracted node
a contracted node
a contracted node
g
Figure 2: Contracting subgraphs in (k +1)-connected components.
Proof. The “only if” direction is trivial since the con-
traction described in Algorithm 1 does not reduce the
connectivity of f.
For the “if” direction, let us assume an f that is
not k-connected. Then there exists a partition V
1
,V
2
of its node set so that |(V
1
,V
2
)| < k. Since the number
m of cactus components C
1
,...,C
m
in T is at least 2,
there exists i ∈ [1,m] s.t. |(V
1
,V
2
) ∩C
i
<
k
2
. Thus, we
have a partition U
1
,U
2
of a node set of f ∩C
i
so that
|(U
1
,U
2
)| <
k
2
.
Let us denote by f
′
:=Contraction(f ∩ C
i
,T).
Since there are at most k cactus edges incident to
f ∩C
i
, w.l.o.g. there are at most
k
2
cactus edges in-
cident to U
1
in f
′
, which we denote by E
′
. Then
(V
1
,V
2
) ∪ E
′
is an edge cut of f
′
of size less than k,
and f
′
is not k-connected.
3.3.2 Extension Procedures
The procedure for f.type = node is described in Al-
gorithm 2. This procedure simply adds a node or an
edge to an existing subgraph instance within a (k+1)-
connectivity component of D. It uses a basic pre-
existing extension procedure basic-extend(), for in-
stance such as the one in FSG (Kuramochi,Karypis
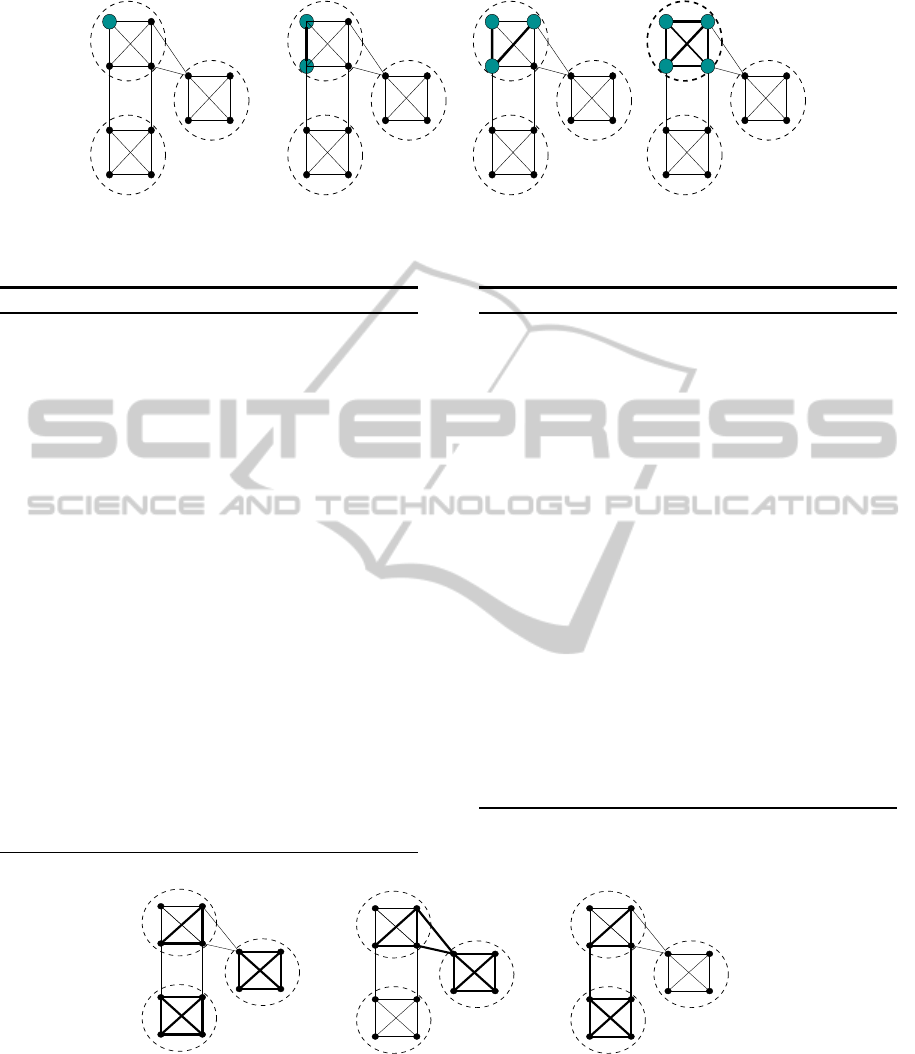
2001). An example of ExtendNodeType() procedure
is given in Figure 3 (extended subgraphs in bold).
The procedure for f.type = cycle is described in
Algorithm 3. It extends an instance f of a frequent
graph within a single cycle C = (V
C
,E
C
) that forms a
node of the cactus dual tree structure. The main con-
cern is to extend a subgraph so as not to create a not-
k-connected instance, and for this purpose the edges
E
C
must be present in an extension. Therefore, a fre-
quent graph instance that is a subgraph of V
C
must be
added to f. An example of joining subgraphs of type
node into subgraphs of type cycle is given in Figure 4
(extended subgraphs in bold).
Algorithm 2: ExtendNodeType().
Input: Cactus T = (V
T
,E
T
) of (k+ 1)-cuts in D,
frequent subgraph f.
Output: extensions of f.
1: Ext( f) :=basic-extend(g);
2: for all h ∈ Ext( f) do
3: if h∩ f.cycle 6= f.cycle then
4: Ext( f) := Ext( f) \ {h};
5: else
6: h.type = node;
7: h.cycle = f.cycle;
8: end if
9: end for
10: return Ext( f);
The final procedure for f.type = tree is described
in Algorithm 4. In this case, f is contained in a sub-
tree of the dual cactus tree structure and it is extended
by an instance of a frequent subgraph of type cycle.
In order not to generate the same instance twice, we
assume that the tree T is a directed out-tree and that
extending a subtree of T by a node is possible only in
the direction of T’s edges. An example of joining two
subgraphs of type cycle into a subgraph of type tree
is given in Figure 5 (extended subgraphs in bold).
3.4 The CactusMining Algorithm
The CactusMining algorithm extends each frequent
graph until it spans beyond connectivity component
of the database, at which point the extension must in-
clude a non-trivial subcactus. If such an extension
is not possible, the frequent subgraph must be aban-
doned. The existence of a counting procedure for sub-
graphs, denoted count(), is assumed.
A FAST ALGORITHM FOR MINING GRAPHS OF PRESCRIBED CONNECTIVITY
9
step 1 step 2
step 3 step 4
Figure 3: Extending frequent subgraphs of type node.
Algorithm 3: ExtendCycleType().
Input: frequent subgraph instances F of type node,
frequent subgraph f.
Output: extensions of f.
1: let C = ({c
1
,...,c
n
},E
C
) := f.cycle;
2: let f ⊆ c
j
;
3: Ext( f) :=
/
0;
4: E =: ∪
i, j
{(c
i
,c
j
) ∈ E
C
} (as edge sets);
5: F
good
:= F ∩C; {frequent subgraphs in C}
6: for all f ∈ F
good
do
7: f
′
:= Contraction(f,C);
8: if f
′
is not k-connected then
9: F
good
:= F
good
\ { f
′
};
10: end if
11: end for
12: for all f
i
∈ F
good
∩ c
i
, 1 ≤ i ≤ n, i 6= j do
13: h := ∪
1≤i≤n, i6= j
f
i
∪ E;
14: if h is a graph then
15: Ext( f) := Ext( f) ∪ {h};
16: h.type = cycle; h.cycle = f.cycle;
17: h.tree = h.cycle;
18: end if
19: end for
20: return Ext( f);
Algorithm 4: ExtendTreeType().
Input: database cactus structure T = (V
T
,E
T
),
frequent subgraph instances F of type cycle,
frequent subgraph f.
Output: extensions of f.
1: T
′
= (V
T
′
,E
T
′
) := f.tree;
2: Ext( f) :=
/
0;
3: for all C ∈ V
T
and C
′
∈ V
T
′
) do
4: if (C
′
,C) ∈ E
T
then
5: for all g ∈ F such that g∩C = f ∩C do
6: T
′′
:= T
′
∪C;
7: g
′
:= Contraction(g ∩C,T
′′
);
8: if g
′
is k-connected then
9: h := f ∪ g;
10: Ext( f) := Ext( f) ∪ {h};
11: h.type = tree;
12: h.tree = (V
T
′
∪ {C},E
T
′
∪ {(C
′
,C)});
13: end if
14: end for
15: end if
16: end for
17: return Ext( f);
g
3
g
2
g
1
g
3
g
2
g
1
g
3
g
2
g
1
g
1
g
2
g
3
g
1
(b)
(c) joining and
joining and
into a subgraph of
into a subgraph of
(a) frequent subgraphs
of type
type
type
node
cycle cycle
Figure 4: Constructing frequent subgraphs of type cycle.
3.5 Proof of Correctness
The aim of this section is to show that every maximal
frequent k-edge-connected subgraph g of G is gener-
ated by the above algorithm at some point (complete-
ness), and no subgraph that is not k-edge-connected is
added to a candidate set (soundness).
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
10

g
1
g
3
g
2
g
2
g
1
g
2
g
1
of type=cycle.
(b) subgraph (a) subgraph
g
3
(a) subgraph
of type=cycle.
from join of and .
of type=tree resulting
Figure 5: Constructing a frequent subgraph of type tree.
Claim 2. The CactusMining algorithm is sound.
Proof. This claim is trivial since step 39 of Algorithm
5 filters out all not-k-connected graphs.
Claim 3. The CactusMining algorithm is complete.
Proof. Let G be a frequent k-connected subgraph of
D, where D has the k-connectivity cactus structure
T. Then every instance of G is contained in a k-
connectivity component of D. Let us assume that
G is not generated by the Algorithm 5 and let G be
minimal in the number of nodes and vertices. We
show that every instance g of G is generated by one of
the procedures ExtendNodeType, ExtendCycleType()
or ExtendTreeType(). If g.type = node, it is gener-
ated by the ExtendNodeType() procedure that filters
out nothing. Otherwise, g.type ∈ {cycle,tree} and by
Claim 1 g is not generated only if g is not-k-connected
- a contradiction.
4 CANDIDATE GRAPHS
GENERATED BY THE
ALGORITHM
In this section, we prove that the CactusMining algo-
rithm is optimal w.r.t. the set of candidate subgraphs
generated by it. We show that any algorithm based on
pattern extension must produce a superset of candi-
date subgraphs generated by the CactusMining algo-
rithm.
Theorem 1. Let AnyAlgorithm be a graph mining al-
gorithm based on pattern extension. Then Cactus-
Mining algorithm produces no more candidates than
AnyAlgorithm.
Proof. We show that any frequent candidate sub-
graph g produced by the CactusMining algorithm has
to be produced by AnyAlgorithm. We denote the
database graph by D and its cactus tree structure by
T = (V
T
,E
T
). We denote the (k + 1)-connectivity of
the cactus structure by C
1
,...,C
n
. Let us assume that
g is produced by the CactusMining algorithm but not
by AnyAlgorithm as a candidate subgraph.
If g ⊆ g
′
, where g
′
is a k-connected frequent graph
in D, then g is produced by AnyAlgorithm (we can
assign labels to g
′
’s nodes so that g is the lexico-
graphically minimal extension of g) – a contradic-
tion. Therefore, g is neither k-connected nor is it
a subgraph of a frequent k-connected graph in D.
Let therefore V
1
,V
2
be a partition of g’s nodes so
that |(V
1
,V
2
)| < k (i.e. an edge cut of size < k sep-
arates V
1
and V
2
). We assume first that g has a
non-empty intersection with cactus nodes C
1
,...,C
m
,
where m > 1. Then g contains all the cactus edges
connectingC
1
,...,C
m
, for otherwise it is not produced
by the CactusMining algorithm (as g.type = cycle or
g.type = node). We denote the edge set (V
1
,V
2
) sep-
arating g by E
1,2
. Since m > 1 and |E
1,2
| < k, there
exists i s.t. |C
i
∩ E
1,2
| <
k
2
. Thus, we have a partition
U
1
,U
2
of a node set of g ∩C
i
so that |(U
1
,U
2
)| <
k
2
.
Let g
′
:=Contraction(g,C
i
). Since there are at most
k cactus edges incident to g ∩C
i
, w.l.o.g. there are at
most
k
2
cactus edges incident to U
1
in g
′
, which we
denote E
′
. Then E
1,2
∪ E
′
is an edge cut of g
′
of size
less than k – in contradiction to step 8 of Algorithm 3
or to step 8 of Algorithm 4. Then g is not produced
by the CactusMining algorithm – a contradiction.
Let us assume now that g ⊆ C
i
for some i ∈ [1, m].
Since g is minimal in the node and edge set, there
exists a node or an edge x such that g − x is either a
k-connected frequent graph in D or is a subset of a
k-connected frequent graph g
′
in D. We can assume
that AnyAlgorithm is locally optimal, and, since Al-
gorithm 2 can use any function as basic-extend(), that
the same function is used. Therefore, g is produced by
both AnyAlgorithm and the CactusMining algorithm
– a contradiction.
A FAST ALGORITHM FOR MINING GRAPHS OF PRESCRIBED CONNECTIVITY
11

Algorithm 5: CactusMining().
Input: graph database D, support S,
connectivity bound k.
Output: frequent k-edge-connected graphs.
1: F
1
:= frequent nodes of D;
2: D := D\ {non-frequent nodes};
3: BuildCactus(D,k− 1);
4: D ← k-connectivity components of D;
5: T := BuildCactus(D, k);
6: F
1
:= frequent nodes; {
type=node
}
7: i := 1;
8: while F
i
6=
/
0 do
9: C
i+1
:=
/
0;
10: for all f ∈ F
i
do
11: C
i+1
:= C
i+1
∪ ExtendNodeType(T, f);
12: end for
13: i := i+ 1;
14: F
i
:= frequent graphs from C
i
;
15: end while
16: F
I
:= ∪
i−1
j=1
F
j
;
17: F
1
:= F
I
; {
type=cycle
}
18: i := 1;
Algorithm 6: CactusMining() contd.
19: while F
i
6=
/
0 do
20: C
i+1
:=
/
0;
21: for all f ∈ F
i
do
22: C
i+1
:= C
i+1
∪ ExtendCycleType(F
I
, f);
23: end for
24: i := i+ 1;
25: F
i
:= frequent graphs from C
i
;
26: end while
27: F
II
:= ∪
i−1
j=1
F
j
;
28: F
1
:= F
II
; {
type=tree
}
29: i := 1;
30: while F
i
6=
/
0 do
31: C
i+1
:=
/
0;
32: for all f ∈ F
i
do
33: C
i+1
:= C
i+1
∪ ExtendTreeType(T,F
II
, f);
34: end for
35: i := i+ 1;
36: F
i
:= frequent graphs from C
i
;
37: end while
38: F
III
:= ∪
i−1
j=1
F
j
;
39: remove < k-connected graphs from F
I
∪ F
II
∪ F
III
;
40: return F
I
∪ F
II
∪ F
III
5 CONCLUSIONS
In this paper, we have presented the CactusMin-
ing algorithm for mining frequent k-edge connected
subgraphs in a graph database, where k is a user-
defined integer constant. The method presented
here is defined and described for a single graph
database case, but is adapted trivially to multiple
graph databases. Our method relies on the Dinitz-
Karzanov-Lomonosov cactus minimum cut structure
theory and on the existence of efficient polynomial
algorithms that compute this structure. Our algorithm
employs the pattern-growth approach, and the cactus
structure of mincuts allows us to grow frequent sub-
graphs by more than a node or an edge at a time. We
haveprovedthat the CactusMining algorithm is sound
and correct, and have also shown that the set of fre-
quent patterns it produces is the least possible, i.e. a
competing graph mining algorithm will produce all
the candidate patterns that our algorithm produces.
ACKNOWLEDGEMENTS
The author thanks the Lynn and William Fraenkel
Center for Computer Science for partially supporting
this work.
REFERENCES
Bixby, R. E. ”The minimum number of edges and vertices
in a graph with edge connectivity n and m n-bonds”,
Networks, 5:253-298, 1975.
Dinits, E. A., Karzanov, A. V., Lomonosov, M. V. ”On the
structure of a family of minimal weighted cuts in a
graph”, Studies in Discrete Optimization (in Russian)
(ed. A.A. Fridman), Nauka, Moscow, 1976, 290-306.
Fleischer, L. ”Building Chain and Cactus Representations
of All Minimum Cuts from Hao-Orlin in the Same
Asymptotic Run Time”, IPCO 1998: 294-309.
Gomory, R. E., Hu, T. C. ”Multi-terminal network flows”,
J. Soc. Indust. Appl. Math, 9(4):551-570, 1991.
Horv´ath, T. and Ramon, J. ”Efficient frequent connected
subgraph mining in graphs of bounded tree-width”,
Theor. Comput. Sci. 411(31-33): 2784-2797, 2010.
Karger, D. R. and Stein, C. ”A new approach to the min-
imum cut problem”, Journal of the ACM, 43(4):601-
640, 1996.
Karger, D. R. and Panigrahi, D. ”A near-linear time algo-
rithm for constructing a cactus representation of min-
imum cuts”, SODA 2009, 246-255.
Karzanov, A. V. and Timofeev, E. A. ”Efficient algorithms
for finding all minimal edge cuts of a nonoriented
graph”, Cybernetics, 22:156-162, 1986. Translated
from Kibernetika 2 (1986) 8-12.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
12

Kuramochi, M. and Karypis, G. ”Frequent Subgraph Dis-
covery”, ICDM 2001: 313-320.
Papadopoulos, A., Lyritsis, A. and Manolopoulos, Y. ”Sky-
graph: an algorithm for important subgraph discov-
ery in relational graphs”, Data Mining and Knowledge
Discovery, 17(1), 2008.
Seeland, M., Girschick, T., Buchwald, F. and Kramer, S.
”Online Structural Graph Clustering Using Frequent
Subgraph Mining”, ECML/PKDD (3) 2010: 213-228.
Yan, X., Zhou, X. J., and Han, J. ”Mining Closed Relational
Graphs with Connectivity Constraints”, ICDE 2005:
357-358.
Zhang, S., Li, S. and Yang, J. ”GADDI: distance in-
dex based subgraph matching in biological networks”,
EDBT 2009: 192-203.
A FAST ALGORITHM FOR MINING GRAPHS OF PRESCRIBED CONNECTIVITY
13
