AN APPROXIMATED EXPRESSION FOR THE CONVERGENCE
TIME OF ADAPTIVE BLIND EQUALIZERS
Monika Pinchas
Department of Electrical and Electronic Engineering, Ariel University Center, 40700 Ariel, Israel
Keywords:
Blind deconvolution, Blind equalization, Acquisition time.
Abstract:
In this paper, closed-form approximated expressions are proposed for the convergence time (or number of
iterations required for convergence) and for the Intersymbol Interference (ISI) as a function of time valid
during the stages of the iterative deconvolution process. The new derivations are valid for the noiseless, real
and two independent quadrature carrier case and for type of blind equalizers where the error that is fed into
the adaptive mechanism which updates the equalizer’s taps can be expressed as a polynomial function of order
three of the equalized output like in Godard’s algorithm. Up to now, the equalizer’s performance (convergence
time and ISI as a function of time) could be obtained only via simulation when the channel coefficients were
known. The new proposed expressions are based on the knowledge of the initial ISI and channel power (which
is measurable) and eliminate the need to carry out any more the above mentioned simulation.
1 INTRODUCTION
It is well known that ISI (Intersymbol Interference)
is a limiting factor in many communication environ-
ments where it causes an irreducible degradation of
the bit error rate (BER) thus imposing an upper limit
on the data symbol rate. In order to overcome the ISI
problem, an equalizer is implemented in those sys-
tems.
The paper is organized as follows: After having de-
scribed the system under consideration in Section 2,
the closed-form approximated expression for the ISI
as a function of time is introduced in Section 3. In
Section 4 simulation results are presented and the
conclusion is given in Section 5.
2 SYSTEM DESCRIPTION
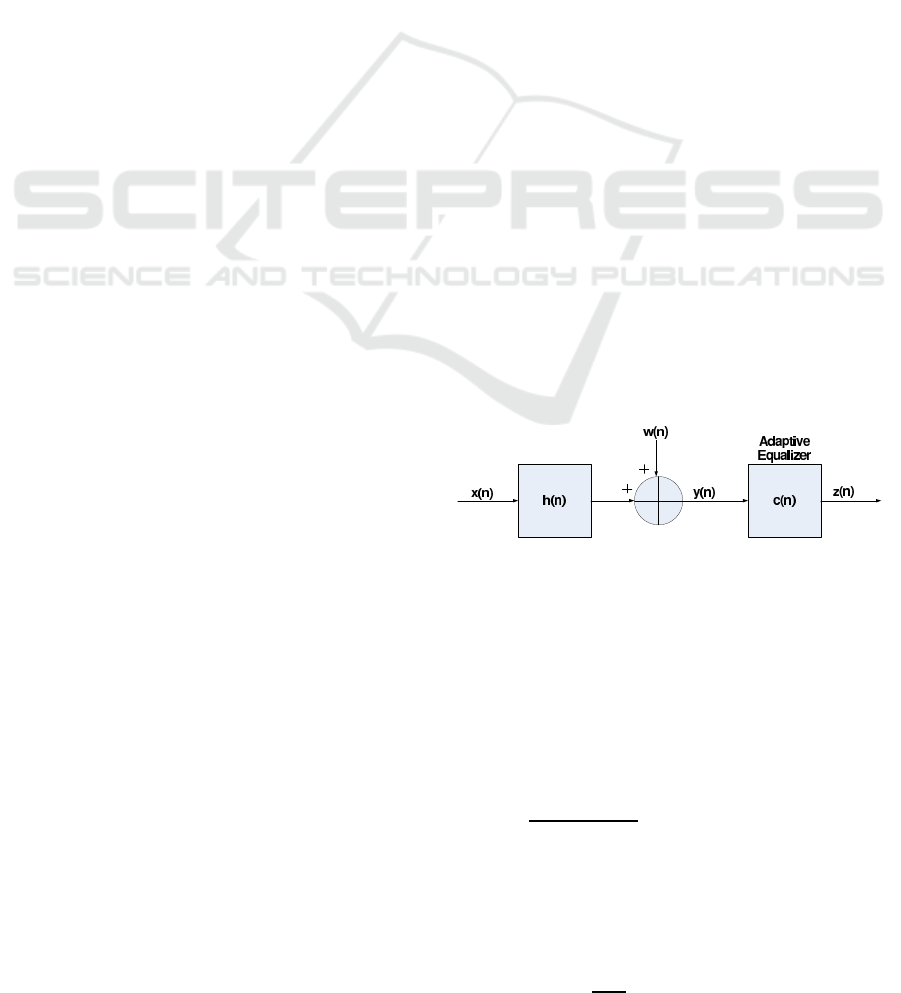
The system under consideration is illustrated in Fig.1,
where we make the following assumptions:
1. The input sequence x[n] belongs to a real or two
independent quadrature carrier case constellation in-
put with variance σ
2
x
where x
1
[n] and x
2
[n] are the real
and imaginary parts of x[n] respectively.
2. The unknown channel h[n] is a possibly nonmin-
imum phase linear time-invariant filter in which the
transfer function has no “deep zeros”, namely, the ze-
ros lie sufficiently far from the unit circle.
3. The equalizer c[n] is a tap-delay line.
4. The noise w[n] is an additive Gaussian white
noise with zero mean and variance σ
2
w
= E[w[n]w
∗
[n]]
(E[·] is the expectation operator). The sequence x[n]
Figure 1: Block diagram of a baseband communication sys-
tem.
is transmitted through the channel h[n] and is cor-
rupted with noise w[n]. The equalized output is de-
fined as: z[n] = x[n] + p[n] + ˜w[n] where p[n] is the
convolutional noise, namely, the residual intersym-
bol interference (ISI) arising from the difference be-
tween the guess c
g
[n] and ideal value c[n] and ˜w[n] =
w[n] ∗ c
g
[n]. The ISI is often used as a measure of
performance in equalizers’ applications, defined by:
ISI[n] =
∑
˜m
| ˜s[ ˜m]|
2
−| ˜s|
2
max
| ˜s|
2
max
where |˜s|
max
is the component
of ˜s, given by ˜s[n] = c
g
[n] ∗ h[n], having the maxi-
mal absolute value. Next we turn to the adaptation
mechanism of the equalizer which is based on a pre-
defined cost function F[n] that characterizes the in-
tersymbol interference, see (Godard, 1980), (Pinchas,
2011) and (Shalvi and Weinstein, 1990). In this paper
we assume that
∂F[n]
∂z[n]
can be expressed as a polyno-
mial function of order three of the equalized output
411
Pinchas M..
AN APPROXIMATED EXPRESSION FOR THE CONVERGENCE TIME OF ADAPTIVE BLIND EQUALIZERS.
DOI: 10.5220/0003529204110414
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 411-414
ISBN: 978-989-8425-74-4
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

namely as P(z[n]). Thus we may write: c
eq
[n+ 1] =
c
eq
[n] − µ
∂F[n]
∂z[n]
y
∗
[n] = c
eq
[n] − µP(z[n]) y
∗
[n] where µ
is the step-size parameter, c
eq
[n] is the equalizer vec-
tor where the input vector is y[n] = [y[n] . . . y[n − L+
1]]
T
and L is the equalizer’s tap length. The opera-
tor ()
T
denotes for transpose of the function (). The
real part of P(z[n]) may be expressed as: P
r
(z[n]) =
a
1
(x
r
+ p
r
[n]) + a
3
(x
r
+ p
r
[n])
3
+
a
12
(x
r
+ p
r
[n])(x
i
+ p
i
[n])
2
where x
r
= x
1
[n], x
i
=
x
2
[n], p
r
[n] and p
i
[n] are the real and imaginary parts
of p[n] respectively and a
1
, a
12
, a
3
are parameters
of the chosen equalizer. In the latter stages where
the blind equalizer has converged we may write that
E[p
2
[n + 1]]
∼
=
E[p
2
[n]]. Since we deal with the
real or two independent quadrature carrier case we
may assume as was done in (Pinchas, 2009) that
E[p
2
r
[n]] = E[p
2
i
[n]]. Thus, in the latter stages where
the blind equalizer has converged we have E[p
2
r
[n+
1]]
∼
=
E[p
2
r
[n]]. Recently, an expression for E[∆p
2
r
] =
E[p
2
r
[n+ 1] − p
2
r
[n]] was derived in (Pinchas, 2009):
E[∆p
2
r
]
∼
=
B(D
1
Bm
3
p
[n] + A
1
m
2
p
[n] + B
1
m
p
[n] +C
1
B)
(1)
where B
1
, B, D
1
, A
1
and C
1
are defined in (Pin-
chas, 2009). E[p
2
r
[n]] = m
p
[n], E[(x
1
[n])
2
] = σ
2
x
r
,
E[(x
2
[n])
2
] = σ
2
x
i
and R is the channel length. With
the help of E[∆p
2
r
] defined in (1), the ISI as a function
of time can be obtained.
3 ISI AS A FUNCTION OF TIME
We start our derivations for the very low ISI case
where the eye diagram is almost open or already open
and then turn to the more general case where the
initial ISI can have much higher values (where the
eye diagram is very closed). Since we deal with the
real and two independent quadrature carrier case, we
start our derivations first with the real valued case and
then turn to the two independent quadrature carrier
case.
The following (additional) assumptions are made:
1. The convolutional noise p[n], is a zero mean, white
Gaussian process with variance σ
2
p
[n] = E[p[n]p
∗
[n]].
2. The source signal x[n] is an independent non-
Gaussian signal with known variance and higher
moments.
3. The convolutional noise p[n] and the source signal
are independent. Thus,
σ
2
z
[n] = E[z[n]z
∗
[n]] = E[(x[n] + p[n])(x[n] +
p[n])
∗
] = E[x[n]x
∗
[n]] + E[p[n]p
∗
[n]]
For the very low ISI case ( B(D
1
Bm
3
p
[n] +
A
1
m
2
p
[n]) ≪ B(B
1
m
p
[n] +C
1
B)) we may approximate
(1) as follows:
E
[
∆p
2
r
]
∆t
∼
=
BB
1
∆t
m
p
[n] +
B
2
C
1
∆t
(2)
Note that for the real valued and two independent
quadrature carrier case we may write: m
p
[n] = σ
2
x
r
·
ISI[n] for | ˜s|
2
max
= 1. By using ISI[n] =
m
p
[n]
σ
2
x
r
(for | ˜s|
2
max
= 1 ), the solution of (2) is given by:
˜m
p
(t)
∼
=
σ
2
x
r
f
ISI(0) +
BC
1
B
1
σ
2
x
r
e
BtB
1
∆t
−
BC
1
B
1
(3)
where
f
ISI(0) is the ISI for the continues time case
obtained at t = 0. Now, by using again that ISI[n] =
m
p
[n]
σ
2
x
r
(for | ˜s|
2
max
= 1 ) and (3) we obtain:
f
ISI(t) =
˜m
p
(t)
σ
2
x
r
∼
=
f
ISI(0) +
BC
1
B
1
σ
2
x
r
e
BtB
1
∆t
−
BC
1
B
1
σ
2
x
r
(4)
As it was already implied, the obtained expression for
the ISI as a function of time given by (4) is only valid
for the very low ISI case where the eye-diagram is
almost open or already open. Obviously, this is not
a case of interest. But in order to obtain a practical
approximated expression for the ISI as a function of
time valid during the whole convergence process of
the equalizer, the expression of (4) was modified as
follows:
f
ISI(t)
∼
=
f
ISI(0) − 10
ISI
r
10
e
γBtB
1
∆t
+ 10
ISI
r
10
(5)
where γ is given by: γ =
min
1
σ
2
x
r
r
B
1
BD
1
,
1
σ
2
x
r
B
1
A
1
1
f
ISI(0)L
and ISI
r
is
the residual ISI expressed in dB units and is defined
for |˜s|
2
max
= 1 in (Pinchas, 2009). It should be pointed
out that (5) is only ad-hoc approximation. Although
this expression (5) was not obtained based on strong
mathematical foundations, it is still interesting to
see the steps that lead to (5). This is exactly what
is done in the following. Since it was already
implied in (Pinchas, 2009) that the expression for
the residual ISI from (4) defined by
−BC
1
B
1
σ
2
x
r
is less
accurate than ISI
r
, it was reasonable to use in (5)
the most accurate expression for the residual ISI that
approximately is known. Next we go back to (1) and
derive some conditions that may lead approximately
to (2). Note that (4) was obtained by assuming the
approximation of (2). In order to get approximately
the expression of (2) from (1), the following con-
ditions should hold:|B
2
Dm
3
p
[n]| << |BB
1
m
p
[n]| and
|A
1
Bm
2
p
[n]| << |BB
1
m
p
[n]| which lead by using the
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
412

relation of ISI[n] =
m
p
[n]
σ
2
x
r
to:
ISI[n] << min
1
σ
2
x
r
r
B
1
BD
,
1
σ
2
x
r
B
1
A
1
(6)
Now, we may say that if the above condition holds,
the obtained expression in (4) for the ISI as a func-
tion of time is approximately valid. Please note that
for the very low ISI case, the convergence time of an
equalizer is much faster compared to the case where
the initial ISI is considered high. In addition, accord-
ing to (Lee and Messerschmitt, 1997), the best rate of
convergenceis dependent on the number of filter coef-
ficients. The more coefficients (in the equalizer), the
longer it takes for the coefficients to converge. The
more coefficients there are, the more ”noise” is intro-
duced into the adaptation of each coefficient by the
simultaneous adaptation of the other coefficients (Lee
and Messerschmitt, 1997). Now, let us go back to the
function of γ in (5). It can be seen that γ functions
as an compensation factor between the very low ISI
condition (6) and any other given initial ISI. There-
fore, when the initial ISI is much higher than given in
(6), γ will slow down the convergence rate.
Next we turn to calculate the total iteration number
that takes to enter the convergence state. The ex-
ponent from (5) can be written as follows: e
γ
BtB
1
∆t
=
e
t
∆t
γBB
1
= e
−
t
τ
where τ = |
∆t
γBB
1
|. Next we assume that
for t = 8τ the equalizer has approximately reached
its steady state position. Note that for a simple RC
circuit (one capacitor and one resistor), it is often as-
sumed that the capacitor is approximatelyfull charged
or discharged after 5τ = 5RC seconds. Since we are
looking for a more accurate solution we choose in-
stead of 5τ, 8τ which was found by simulation tri-
als leading to satisfying results. Thus we may write:
t = 8τ = 8|
∆t
γBB
1
| Now let the sampling time be ∆t.
Thus we may write that t = n∆t = 8|
∆t
γBB
1
| from which
we obtain (for ∆t 6= 0) the total number of iteration
required for convergence:
n =
f
ISI(0)L
min
1
σ
2
x
r
r
B
1
BD
,
1
σ
2
x
r
B
1
A
1
8
B
|
1
B
1
| (7)
4 SIMULATION
In the following we use Godard’s equalizer (Go-
dard, 1980) and the 16QAM constellation (a mod-
ulation using ± {1,3} levels for in-phase and
quadrature components) as the source. The equal-
izer taps for Godard’s equalizer (Godard, 1980)
were updated according to: c
l
[n+ 1] = c
l
[n] −
µ
G
|z[n]|
2
−
E
[
|x[n]|
4
]
E
[
|x[n]|
2
]
z[n] y
∗
[n− l] where µ
G
is the
step-size and l is the equalizer’s tap length. The val-
ues for a
1
, a
12
and a
3
corresponding to Godards’s
(Godard, 1980) algorithm were defined as a
G
1
, a
G
12
and
a
G
3
respectively and were given by: a
G
1
= −
E
[
|x[n]|
4
]
E
[
|x[n]|
2
]
,
a
G
12
= 1 and a
G
3
= 1. Two different channels were con-
sidered.
Channel1 (initial ISI = 0.44): The channel param-
eters were determined according to (Shalvi and Wein-
stein, 1990): h
n
= 0 for n < 0; −0.4 for n =
0 0.84· 0.4
n−1
for n > 0.
Channel2 (initial ISI = 0.5): The channel parame-
ters were determined according to (Fiori, 2001):
h
n
= (−0.0144, 0.0006, 0.0427, 0.0090,
−0.4842, −0.0376, 0.8163, 0.0247, 0.2976, 0.0122,
0.0764, 0.0111, 0.0162, 0.0063)
For Channel1 and Channel2 an equalizer with 13 and
21 taps was used respectively. In the simulation,
the equalizer was initialized by setting the center tap
equal to one and all others to zero. Fig. 2 and Fig. 3
show the simulated performance of Godard’s equal-
ization method for the 16QAM input case, namely
the ISI as a function of iteration number for vari-
ous step-size parameters, channel characteristics and
equalizer’s tap length, compared with the calculated
ISI as a function of iteration number (5) proposed in
this paper. According to Fig. 2 and Fig. 3, the ap-
proximated closed-form expression for the ISI as a
function of time (or iteration number) (5), fits very
well the simulated results. Next, the expression for
the total number of iteration required for convergence
(7) was calculated for each simulation:
Case I – Described in Figure 2. The calculated
number of iteration required for convergence accord-
ing to (7) is 3135.
Case II – Described in Figure 3. The calculated
number of iteration required for convergence accord-
ing to (7) is 1788.
According to Fig. 2 and Fig. 3, there is a high
correlation between the simulated and calculated (7)
results for the number of iteration required for con-
vergence.
Next we turn to the noisy case situation. Fig.4
shows the simulated performance of Godard’s equal-
ization method for the 16QAM input case, namely the
ISI as a function of iteration number for various SNR
values, compared with the calculated ISI as a func-
tion of iteration number (5) proposed in this paper.
AN APPROXIMATED EXPRESSION FOR THE CONVERGENCE TIME OF ADAPTIVE BLIND EQUALIZERS
413
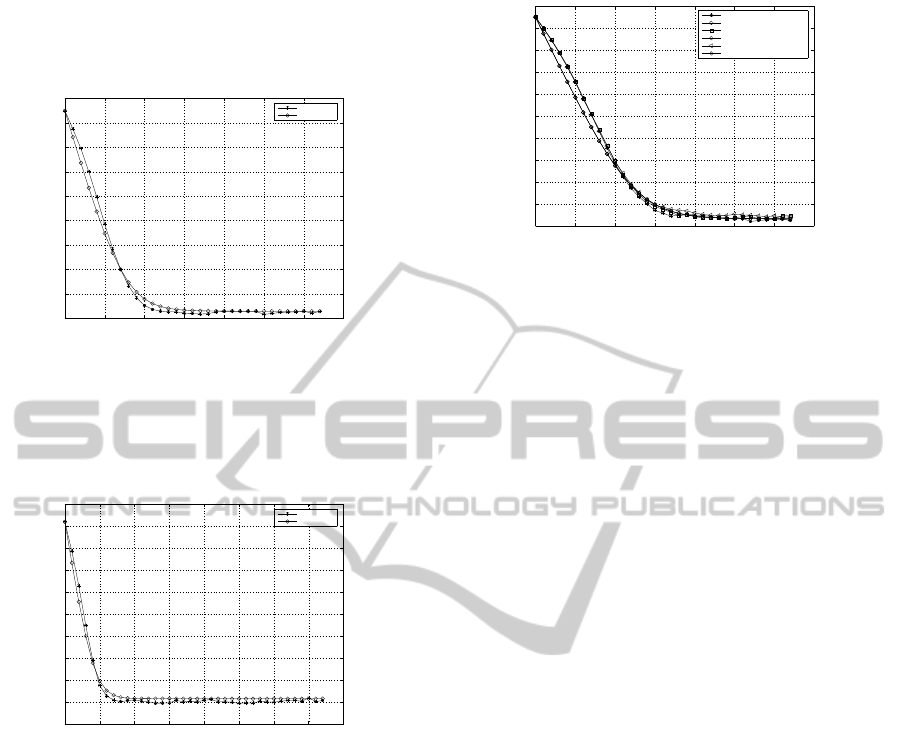
According to Fig.4, the approximated expression for
the ISI as a function of iteration number (5) is valid
also for the noisy case.
0 1000 2000 3000 4000 5000 6000 7000
−20
−18
−16
−14
−12
−10
−8
−6
−4
−2
Iteration Number
ISI [dB]
Simulated ISI
Cal ISI
Figure 2: A comparison between the simulated (with Go-
dard’s algorithm) and calculated ISI as a function of time
for the 16QAM source input going through channel2. The
averaged results were obtained in 100 Monte Carlo trials for
the noiseless case. The equalizer’s length was set to 21 and
µ
G
= 0.00003.
0 1000 2000 3000 4000 5000 6000 7000 8000
−22
−20
−18
−16
−14
−12
−10
−8
−6
−4
−2
Iteration Number
ISI [dB]
Simulated ISI
Cal ISI
Figure 3: A comparison between the simulated (with Go-
dard’s algorithm) and calculated ISI as a function of time
for the 16QAM source input going through channel1. The
averaged results were obtained in 100 Monte Carlo trials for
the noiseless case. The equalizer’s length was set to 13 and
µ
G
= 0.00005.
5 CONCLUSIONS
In this paper, a closed-form approximated expression
was proposed for the (ISI) as a function of time for
type of blind equalizers where the error that is fed
into the adaptive mechanism which updates the equal-
izer’s taps can be expressed as a polynomial func-
tion of the equalized output of order three. Based
on the closed-form approximated expression for the
ISI as a function of time, an approximated closed-
form expression for the convergence time (or num-
ber of iteration required for convergence) as a func-
tion of initial ISI, step-size parameter, equalizer’s tap
length, input signal statistics and channel power was
0 1000 2000 3000 4000 5000 6000 7000
−22
−20
−18
−16
−14
−12
−10
−8
−6
−4
−2
Iteration Number
ISI [dB]
Simulated ISI for SNR=30 [dB]
Cal ISI
Simulated ISI for SNR=25 [dB]
Cal ISI
Simulated ISI for SNR=22 [dB]
Cal ISI
Figure 4: A comparison between the simulated (with Go-
dard’s algorithm) and calculated ISI as a function of time
for the 16QAM source input going through channel2. The
averaged results were obtained in 100 Monte Carlo trials
for the noisy case. The equalizer’s length was set to 21 and
µ
G
= 0.00002.
derived. The new closed-form approximated expres-
sions were tested via simulation where high correla-
tion was found between the calculated and simulated
results. These results indicate that the need to sim-
ulate the whole system in order to find the conver-
gence time or the ISI as a function of time for each
different step-size parameter is eliminated. Although
the approximated expression for the ISI as a function
of time was derived for the noiseless case, simulation
results have shown that it is valid also for the noisy
condition.
REFERENCES
Fiori, S. (2001). A contribution to (neuromorphic) blind
deconvolution by flexible approximated bayesian esti-
mation. In Signal Processing 81, 2131–2153. Elsevier.
Godard, D. (1980). Self recovering equalization and car-
rier tracking in two-dimentional data communication
system. In IEEE Transaction Communication 28 (11)
1867-1875. IEEE.
Lee, E. A. and Messerschmitt, D. G. (1997). Adaptive
Equalization, in: E. A. Lee and D. G. Messerschmitt,
Digital Communication. Kluwer Academic Publisher,
third printing, 2nd edition.
Pinchas, M. (2009). A closed approximated formed
expression for the achievable residual intersym-
bol interference obtained by blind equalizers.
In Signal Processing Journal (Eurasip), DOI:
10.1016/j.sigpro.2009.12.014.
Pinchas, M. (2011). A mse optimized polynomial equal-
izer for 16qam and 64qam constellation. In Signal,
Image and Video Processing, Volume 5, Issue 1, DOI
10.1007/s11760-009-0138-z.
Shalvi, O. and Weinstein, E. (1990). New criteria for blind
deconvolution of nonminimum phase systems (chan-
nels). In IEEE Trans. Information Theory 36 (2), 312-
321.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
414
