
SELF-ADAPTIVE INTEGER AND DECIMAL MUTATION
OPERATORS FOR GENETIC ALGORITHMS
Ghodrat Moghadampour
Vaasa University of Applied Sciences, Wolffintie 30, 65200 Vaasa, Finland
Keywords: Evolutionary algorithm, Genetic algorithm, Function optimization, Mutation operator, Self-adaptive
mutation operators, Integer mutation operator, Decimal mutation operator, Fitness evaluation and analysis.
Abstract: Evolutionary algorithms are affected by more parameters than optimization methods typically. This is at the
same time a source of their robustness as well as a source of frustration in designing them. Adaptation can
be used not only for finding solutions to a given problem, but also for tuning genetic algorithms to the
particular problem. Adaptation can be applied to problems as well as to evolutionary processes. In the first
case adaptation modifies some components of genetic algorithms to provide an appropriate form of the
algorithm, which meets the nature of the given problem. These components could be any of representation,
crossover, mutation and selection. In the second case, adaptation suggests a way to tune the parameters of
the changing configuration of genetic algorithms while solving the problem. In this paper two new self-
adaptive mutation operators; integer and decimal mutation are proposed for implementing efficient
mutation in the evolutionary process of genetic algorithm for function optimization. Experimentation with
27 test cases and 1350 runs proved the efficiency of these operators in solving optimization problems.
1 INTRODUCTION
Evolutionary algorithms are heuristic algorithms,
which imitate the natural evolutionary process and
try to build better solutions by gradually improving
present solution candidates. It is generally accepted
that any evolutionary algorithm must have five basic
components: 1) a genetic representation of a number
of solutions to the problem, 2) a way to create an
initial population of solutions, 3) an evaluation
function for rating solutions in terms of their
“fitness”, 4) “genetic” operators that alter the
genetic composition of offspring during
reproduction, 5) values for the parameters, e.g.
population size, probabilities of applying genetic
operators (Michalewicz, 2000).
Genetic algorithm is an evolutionary algorithm,
which starts the solution process by randomly
generating the initial population and then refining
the present solutions through natural like operators,
like crossover and mutation. The behaviour of the
genetic algorithm can be adjusted by parameters,
like the size of the initial population, the number of
times genetic operators are applied and how these
genetic operators are implemented. Deciding on the
best possible parameter values over the genetic run
is a challenging task, which has made researchers
busy with developing even better and efficient
techniques than the existing ones.
2 GENETIC ALGORITHM
Most often genetic algorithms (GAs) have at least
the following elements in common: populations of
chromosomes, selection according to fitness,
crossover to produce new offspring, and random
mutation of new offspring.
A simple GA works as follows: 1) A population
of
l
-bit strings (chromosomes) is randomly
generated, 2) the fitness
)(xf
of each
chromosome
x
in the population is calculated, 3)
chromosomes are selected to go through crossover
and mutation operators with
p
c
and
p
m
probabilities
respectively, 4) the old population is replace by the
new one, 5) the process is continued until the
termination conditions are met.
However, more sophisticated genetic algorithms
typically include other intelligent operators, which
apply to the specific problem. In addition, the whole
algorithm is normally implemented in a novel way
with user-defined features while for instance
184
Moghadampour G..
SELF-ADAPTIVE INTEGER AND DECIMAL MUTATION OPERATORS FOR GENETIC ALGORITHMS.
DOI: 10.5220/0003494401840191
In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 184-191
ISBN: 978-989-8425-54-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

measuring and controlling parameters, which affect
the behaviour of the algorithm
.
2.1 Genetic Operators
For any evolutionary computation technique, the
representation of an individual in the population and
the set of operators used to alter its genetic code
constitute probably the two most important
components of the system. Therefore, an appropriate
representation (encoding) of problem variables must
be chosen along with the appropriate evolutionary
computation operators. The reverse is also true;
operators must match the representation. Data might
be represented in different formats: binary strings,
real-valued vectors, permutations, finite-state
machines, parse trees and so on. Decision on what
genetic operators to use greatly depends on the
encoding strategy of the GA. For each
representation, several operators might be employed
(Michalewicz, 2000). The most commonly used
genetic operators are crossover and mutation. These
operators are implemented in different ways for
binary and real-valued representations. In the
following, these operators are described in more
details.
2.1.1 Crossover
Crossover is the main distinguishing feature of a
GA. The simplest form of crossover is single-point:
a single crossover position is chosen randomly and
the parts of the two parents after the crossover
position are exchanged to form two new individuals
(offspring). The idea is to recombine building blocks
(schemas) on different strings. However, single-
point crossover has some shortcomings. For
instance, segments exchanged in the single-point
crossover always contain the endpoints of the
strings; it treats endpoints preferentially, and cannot
combine all possible schemas. For example, it
cannot combine instances of 11*****1 and
****11** to form an instance of 11***11*
(Mitchell, 1998). Moreover, the single-point
crossover suffers from “positional bias” (Mitchell,
1998): the location of the bits in the chromosome
determines the schemas that can be created or
destroyed by crossover.
Consequently, schemas with long defining
lengths are likely to be destroyed under single-point
crossover. The assumption in single-point crossover
is that short, low-order schemas are the functional
building blocks of strings, but the problem is that the
optimal ordering of bits is not known in advance
(Mitchell, 1998). Moreover, there may not be any
way to put all functionally related bits close together
on a string, since some particular bits might be
crucial in more than one schema. This might happen
if for instance in one schema the bit value of a locus
is 0 and in the other schema the bit value of the
same locus is 1. Furthermore, the tendency of
single-point crossover to keep short schemas intact
can lead to the preservation of so-called hitchhiker
bits. These are bits that are not part of a desired
schema, but by being close on the string, hitchhike
along with the reproduced beneficial schema
(Mitchell, 1998).
In two-point crossover, two positions are chosen
at random and the segments between them are
exchanged. Two-point crossover reduces positional
bias and endpoint effect, it is less likely to disrupt
schemas with large defining lengths, and it can
combine more schemas than single-point crossover
(Mitchell, 1998). Two-point crossover has also its
own shortcomings; it cannot combine all schemas.
Multipoint-crossover has also been implemented,
e.g. in one method, the number of crossover points
for each parent is chosen from a Poisson distribution
whose mean is a function of the length of the
chromosome. Another method of implementing
multipoint-crossover is the “parameterized uniform
crossover” in which each bit is exchanged with
probability
p , typically
8.05.0 ≤≤ p
(Mitchell,
1998). In parameterized uniform crossover, any
schemas contained at different positions in the
parents can potentially be recombined in the
offspring; there is no positional bias. This implies
that uniform crossover can be highly disruptive of
any schema and may prevent coadapted alleles from
ever forming in the population (Mitchell, 1998).
There has been some successful experimentation
with a crossover method, which adapts the
distribution of its crossover points by the same
process of survival of the fittest and recombination
(Michalewicz, 2000). This was done by inserting
into the string representation special marks, which
keep track of the sites in the string where crossover
occurred. The hope was that if a particular site
produces poor offspring, the site dies off and vice
versa.
The one-point and uniform crossover methods
have been combined by some researchers through
extending a chromosomal representation by
additional bit. There has also been some
experimentation with other crossovers: segmented
crossover and shuffle crossover (Eshelman and
SELF-ADAPTIVE INTEGER AND DECIMAL MUTATION OPERATORS FOR GENETIC ALGORITHMS
185

Schaffer, 1991; Michalewicz, 2000). Segmented
crossover, a variant of the multipoint, allows the
number of crossover points to vary. The fixed
number of crossover points and segments (obtained
after dividing a chromosome into pieces on
crossover points) are replaced by a segment switch
rate, which specifies the probability that a segment
will end at any point in the string. The shuffle
crossover is an auxiliary mechanism, which is
independent of the number of the crossover points.
It 1) randomly shuffles the bit positions of the two
strings in tandem, 2) exchanges segments between
crossover points, and 3) unshuffles the string
(Michalewicz, 2000). In gene pool recombination,
genes are randomly picked from the gene pool
defined by the selected parents.
There is no definite guidance on when to use
which variant of crossover. The success or failure of
a particular crossover operator depends on the
particular fitness function, encoding, and other
details of GA. Actually, it is a very important open
problem to fully understand interactions between
particular fitness function, encoding, crossover and
other details of a GA. Commonly, either two-point
crossover or parameterized uniform crossover has
been used with the probability of occurrence
8.07.0 −≈p
(Mitchell, 1998).
Generally, it is assumed that crossover is able to
recombine highly fit schemas. However, there is
even some doubt on the usefulness of crossover, e.g.
in schema analysis of GA, crossover might be
considered as a “macro-mutation” operator that
simply allows for large jumps in the search space
(Mitchell, 1998).
2.1.2 Mutation
The common mutation operator used in canonical
genetic algorithms to manipulate binary strings
A
A
}1,0{),...(
1
=∈= Iaaa
of fixed length A was
originally introduced by Holland (Holland, 1975)
for general finite individual spaces
A
AAI ...
1
×
=
,
where
},...,{
1
l
k
iii
A
α
α
=
. By this definition, the
mutation operator proceeds by:
i. determining the position
}),...,1{(,...,
1
liii
jh
∈
to
undergo mutation by a uniform random
choice, where each position has the same
small probability
m
p of undergoing mutation,
independently of what happens at other
position
ii. forming the new vector
),...,,,...,,,,...,(
11
1
1
1
1
1
1 A
a
i
a
i
a
i
aa
i
aaa
i
a
hhh
ii
+−
+−
′
′
=
′
, where
ii
Aa
∈
′
is drawn uniformly at random from the
set of admissible values at position
i .
The original value
i
a at a position undergoing
mutation is not excluded from the random choice of
ii
Aa ∈
′
. This implies that although the position is
chosen for mutation, the corresponding value might
not change at all (Bäck, Fogel, Whitely, Angeline,
2000).
Mutation rate is usually very small, like 0.001
(Mitchell 1998). A good starting point for the bit-
flip mutation operation in binary encoding is
L
P
m
1
=
,
where
L is the length of the chromosome
(Mühlenbein, 1992). Since
L
1
corresponds to
flipping one bit per genome on average, it is used as
a lower bound for mutation rate. A mutation rate of
range
[
]
01.0,005.0∈
m
P
is recommended for binary
encoding (Ursem, 2003). For real-value encoding
the mutation rate is usually
[]
9.0,6.0∈
m
P
and the
crossover rate is
[
]
0.1,7.0∈
m
P
(Ursem, 2003).
Crossover is commonly viewed as the major
instrument of variation and innovation in GAs, with
mutation, playing a background role, insuring the
population against permanent fixation at any
particular locus (Mitchell, 1998), (Bäck et al., 2000).
Mutation and crossover have the same ability for
“disruption” of existing schemas, but crossover is a
more robust constructor of new schemas (Spears,
1993; Mitchell, 1998). The power of mutation is
claimed to be underestimated in traditional GA,
since experimentation has shown that in many cases
a hill-climbing strategy works better than a GA with
crossover (Mühlenbein, 1992; Mitchell, 1998).
While recombination involves more than one
parent, mutation generally refers to the creation of a
new solution form one and only one parent. Given a
real-valued representation where each element in a
population is an
n -dimensional vector
n
x ℜ∈
,
there are many methods for creating new offspring
using mutation. The general form of mutation can be
written as:
)(xmx
=
′
,
(1)
where
x
is the parent vector, m is the mutation
function and
x
′
is the resulting offspring vector. The
more common form of mutation generated offspring
vector:
Mxx +=
′
,
(2)
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
186

where the mutation
M
is a random variable.
M
has
often zero mean such that
xxE =
′
)( .
(3)
the expected difference between the real values of a
parent and its offspring is zero (Bäck et al., 2000).
Some forms of evolutionary algorithms apply
mutation operators to a population of strings without
using recombination, while other algorithms may
combine the use of mutation with recombination.
Any form of mutation applied to a permutation must
yield a string, which also presents a permutation.
Most mutation operators for permutations are related
to operators, which have also been used in
neighbourhood local search strategies (Whitley,
2000). Some other variations of the mutation
operator for more specific problems have been
introduced in Chapter 32 in (Bäck et al., 2000).
Some new methods and techniques for applying
crossover and mutation operators have also been
presented in (Moghadampour, 2006).
It is not a choice between crossover and mutation
but rather the balance among crossover, mutation,
selection, details of fitness function and the
encoding. Moreover, the relative usefulness of
crossover and mutation change over the course of a
run. However, all these remain to be elucidated
precisely (Mitchell, 1998).
2.1.3 Other Operators and Mating
Strategies
In addition to common crossover and mutation there
are some other operators used in GAs including
inversion, gene doubling and several operators for
preserving diversity in the population. For instance,
a “crowding” operator has been used in (De Jong,
1975), (Mitchell, 1998) to prevent too many similar
individuals (“crowds”) from being in the population
at the same time. This operator replaces an existing
individual by a newly formed and most similar
offspring. In (Mengshoel and Goldberg, 2008) a
probabilistic crowding niching algorithm in which
subpopulations are maintained reliably, is presented.
It is argued that like the closely related deterministic
crowding approach, probabilistic crowding is fast,
simple, and requires no parameters beyond those of
classical genetic algorithms.
The same result can be accomplished by using an
explicit “fitness sharing” function (Mitchell 1998),
whose idea is to decrease each individual’s fitness
by an explicit increasing function of the presence of
other similar population members. In some cases,
this operator induces appropriate “speciation”,
allowing the population members to converge on
several peaks in the fitness landscape (Mitchell,
1998). However, the same effect could be obtained
without the presence of an explicit sharing function
(Smith, Forrest and Perelson, 1993; Mitchell, 1998).
Diversity in the population can also be promoted
by putting restrictions on mating. For instance,
distinct “species” tend to be formed if only
sufficiently similar individuals are allowed to mate
(Mitchell, 1998). Another attempt to keep the entire
population as diverse as possible is disallowing
mating between too similar individuals, “incest”
(Eshelman and Schaffer, 1991; Mitchell, 1998).
Another solution is to use a “sexual selection”
procedure; allowing mating only between
individuals having the same “mating tags” (parts of
the chromosome that identify prospective mates to
one another). These tags, in principle, would also
evolve to implement appropriate restrictions on new
prospective mates (Eiben and Schut, 2008).
Another solution is to restrict mating spatially.
The population evolves on a spatial lattice, and
individuals are likely to mate only with individuals
in their spatial neighborhoods. Such a scheme would
help preserve diversity by maintaining spatially
isolated species, with innovations largely occurring
at the boundaries between species (Mitchell 1998).
The efficiency of genetic algorithms has also
been tried by imposing adaptively, where the
algorithm operators are controlled dynamically
during runtime (Eiben and Schut, 2008). These
methods cn be categorized as deterministic,
adaptive, and self-adaptive methods (Eiben and
Smith, 2007; Eiben and Schut, 2008). Adaptive
methods adjust the parameters’ values during
runtime based on feedbacks from the algorithm
(Eiben et al., 2008), which are mostly based on the
quality of the solutions or speed of the algorithm
(Smit and Eiben, 2009).
2.1.4 Other Operators and Mating
Strategies
In addition to common crossover and mutation there
are some other operators used in GAs including
inversion, gene doubling and several operators for
preserving diversity in the population. For instance,
a “crowding” operator has been used in (De Jong,
1975), (Mitchell 1998) to prevent too many similar
individuals (“crowds”) from being in the population
at the same time. This operator replaces an existing
individual by a newly formed and most similar
offspring. In (Mengshoel et al., 2008) a probabilistic
SELF-ADAPTIVE INTEGER AND DECIMAL MUTATION OPERATORS FOR GENETIC ALGORITHMS
187

crowding niching algorithm in which
subpopulations are maintained reliably, is presented.
It is argued that like the closely related deterministic
crowding approach, probabilistic crowding is fast,
simple, and requires no parameters beyond those of
classical genetic algorithms.
The same result can be accomplished by using an
explicit “fitness sharing” function (Mitchell 1998),
whose idea is to decrease each individual’s fitness
by an explicit increasing function of the presence of
other similar population members. In some cases,
this operator induces appropriate “speciation”,
allowing the population members to converge on
several peaks in the fitness landscape (Mitchell,
1998). However, the same effect could be obtained
without the presence of an explicit sharing function
(Smith et al., 1993; Mitchell, 1998).
Diversity in the population can also be promoted
by putting restrictions on mating. For instance,
distinct “species” tend to be formed if only
sufficiently similar individuals are allowed to mate
(Mitchell 1998). Another attempt to keep the entire
population as diverse as possible is disallowing
mating between too similar individuals, “incest”
(Eshelman and Schaffer 1991; Mitchell, 1998).
Another solution is to use a “sexual selection”
procedure; allowing mating only between
individuals having the same “mating tags” (parts of
the chromosome that identify prospective mates to
one another). These tags, in principle, would also
evolve to implement appropriate restrictions on new
prospective mates (Eiben et al., 2008).
Another solution is to restrict mating spatially.
The population evolves on a spatial lattice, and
individuals are likely to mate only with individuals
in their spatial neighborhoods. Such a scheme would
help preserve diversity by maintaining spatially
isolated species, with innovations largely occurring
at the boundaries between species (Mitchell, 1998).
The efficiency of genetic algorithms has also
been tried by imposing adaptively, where the
algorithm operators are controlled dynamically
during runtime (Eiben et al., 2008). These methods
cn be categorized as deterministic, adaptive, and
self-adaptive methods (Eiben & Smith, 2007; Eiben
et al., 2008). Adaptive methods adjust the
parameters’ values during runtime based on
feedbacks from the algorithm (Eiben et al., 2008),
which are mostly based on the quality of the
solutions or speed of the algorithm (Smit et al.,
2009).
3 SELF-ADAPTIVE MUTATION
OPERATORS
One major problem with the classical
implementation of binary mutation, the multipoint
mutation or the crossover operator is that it is
difficult to control their effect or to restrict changes
caused by them within certain values.
Therefore, several techniques are developed here
to implement the genetic operators intelligently so
that the resulting modifications on the binary string
will cause changes in the real values within the
desired limits. This idea is implemented so that the
real value of the variable is randomly changed
within the desired limits and the modified value then
is converted to the binary representation and stored
as the value of the variable. In this way we can
cause more precise mutations in the bit strings and
make sure that changes in real values are within the
desired bounds.
Apparently, changes of different magnitudes are
required at different stages of the evolutionary
process. Thus, two types of decimal mutation
operators have been implemented:
1. For modifying variables with integer
values. The bounds for the absolute values of
such changes are at least 1 and at most the
integer part of the real value representation of
the variable. This means that the upper bound
of the range may vary even for each variable
of the same individual. The randomly
selected mutation value may be either
positive or negative. Thus, if the integer part
of the variable is
)int(variable , the integer
mutation range is
)int(var,1 iable±
.
2. For modifying variables with values from
the range
(
)
1,0 . The lower bound for the
absolute value of such changes is determined
by the required precision of the real value
presentation of the variable, like
10
6−
. The
upper bound for the absolute value of such
changes is determined by decimal part of the
variable. Here also the mutation value can be
either positive or negative. Thus, if the
number of digits after the decimal point for a
variable is
)varprecision( iable , and the decimal
part of the variable is
)rdecimal(va iable , the
range for the real mutation values is
[
]
)rdecimal(va ,
10
)varprecision(
iable
iable−
±
.
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
188

3.1 The Integer Mutation Operator
The integer mutation (IM) operator mutates the
individuals of the population in relatively great
magnitudes. This operator is naturally applied only
to individuals with integer part equal or greater or
than 1. During this operation an integer mutation
value
Δ is selected randomly from the following
range:
[
]
)(nti ,1 variable±∈Δ
(4)
and added to the variable under mutation. Here,
)(nti variable
stands for the absolute value of the
integer part of the variable. Clearly, this integer part
does not necessarily cover the whole range of the
variable. To avoid wasting resources special care is
taken to make sure that the generated random
number is not 0. Thus, the upper bound for the
integer mutation value is different for each variable
and is defined by the absolute value of the integer
part of the variable. This will make the process more
flexible and smart. If the resulting value of the
variable is outside of its pre-defined variable range,
the change will be rejected.
If the upper bound of the mutation value is set to
a fixed value, the operator becomes inefficient or the
probability for its failure will rise. For instance, if
the optimal value of a variable is 0.05 and its present
value 80.64, we will need 80 successful integer
mutations of magnitude 1 in order to get close to the
optimal value of the variable. However, if the
magnitude of the integer mutation value can be
dynamically determined by the magnitude of the
variable, the operator will have a much greater
chance to improve the value of the variable
dramatically in a short time.
During this operation a randomly generated
integer number within the specified bounds is added
to the value of the variable and the binary
representation of the resulting offspring is updated.
The offspring is then evaluated and put through the
survivor selection procedure. There is no fixed rate
for this operator. All population members go
through this operator at least once.
3.2 The Decimal Mutation Operator
The decimal mutation (DM) operator is used in
order to implement changes of smaller magnitudes
on individuals. This operator is naturally applied
only to variables with decimal part greater than 0.
During this operation non-zero decimal numbers in
the specific range are randomly generated and added
to the randomly selected variables in the individual.
The upper bound for the decimal mutation values is
determined by the absolute value of the decimal part
of variables. If the decimal part of a variable is
denoted by
)decimal(variable
, the maximum distance
of the mutation values from 0 is
)decimal(variable
.
The lower bound of the mutation range is
determined by the number of digits after the decimal
point. Thus, if
)precision(variable shows the number
of required decimal places of a variable, the decimal
mutation value is determined in the following way:
[
]
)rdecimal(va ,
10
)varprecision(
iable
iable−
±
σ
(5)
If the resulting value of the variable is outside of
the pre-defined range of the variable, the change
will be rejected. The difference between this
operator and the integer mutation operator is the
way the mutation value is determined. Otherwise,
these operators are similar.
After each operator application, new offspring
are evaluated and compared to the population
individuals. Newly generated offspring will replace
the worst individual in the population if they are
better than the worst individual. Therefore, the
algorithm is a steady state genetic algorithm.
4 EXPERIMENTATION
The self-adaptive integer and decimal mutation
operators were applied as part of a genetic algorithm
to solve the following minimization problems:
Ackley’s function, Colville’s function, Griewank’s
function F1, Rastrigin’s function, Rosenbrock’s
function and Schaffer’s F6 and F7 functions. For
multidimensional problems with optional number of
dimensions (
n
), the algorithm was tested for
50 ,10 ,5 3, ,2 ,1
=
n
. The population size was set to 9.
The efficiency of the proposed operators was
compared against classical crossover (with 55%-
88% crossover rate) and mutation operator (with 1%
mutation rate). Experimentations were carried out
with three different configurations. In the first
configuration only classical mutation and crossover
operators were used to solve the problems. In the
second configuration classical mutation and
crossover and proposed self-adaptive integer and
decimal mutation operators were used to solve the
problems. Finally, in the third configuration only
proposed self-adaptive integer and decimal mutation
operators were used to solve the problems. For each
SELF-ADAPTIVE INTEGER AND DECIMAL MUTATION OPERATORS FOR GENETIC ALGORITHMS
189
configuration the worst individual in the population
was replaced by a better offspring produced as a
result of applying an operator. Each algorithm was
run 50 times for each problem.
The following table summarises the results of
applying three different sets of operators to solve
functions mentioned earlier. Functions and different
variations of their variables make 27 different test
cases.
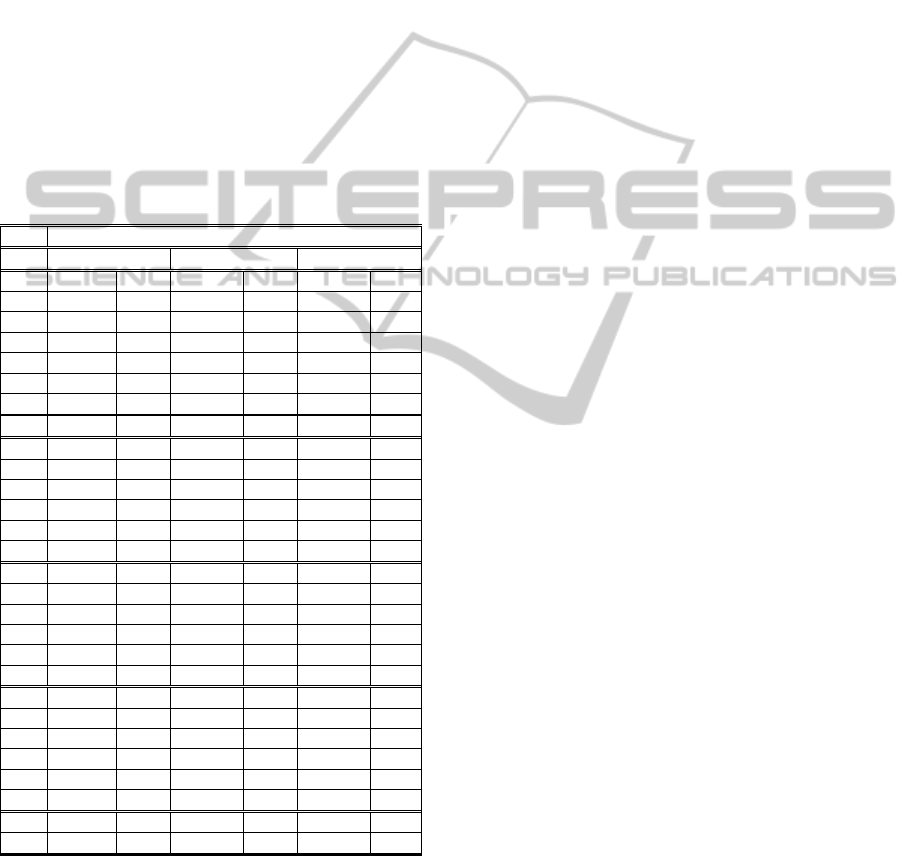
Table 1: Summary of test runs with three different
operator sets: CoMu (crossover & mutation), CoMuImDm
(crossover, mutation, integer mutation & decimal
mutation) and ImDm (integer mutation & decimal
mutation) to solve Ackely’s functions (A1-A50),
Colville’s function (C4), Grienwank’s functions (G1-
G50), Rastrigin’s function (Ra1-Ra50), Rosenbrock’s
function (Ro1-Ro50), Schaffer’s F6 (S62) and F7 (S72)
functions. Fn. stands for function, F. for fitness and FE.
for function evaluation.
Fn.
Operator Set
CoMu CoMuIm_Dm ImDm
F. FE. F. FE. F. FE.
A1 1.12E-06
5804 8.00E-08 3276 4.00E-06
10005
A2 2.98E-01
10017 1.76E-06 8174 4.00E-06
10005
A3 1.440
10009 8.30E-01 9844 8.02E-01
10006
A5 4.390
10015 0.278 10010 1.89
10006
A10 9.495
10009 1.188 10011 3.86
10006
A50 18.754
10019 8.925 10013 10.17
10005
C4 5.486
10012 0.564 5380 1.57
6688
G1 1.10E-03
5960 0.000 1740 7.89E-04
2723
G2 0.022
9998 0.017 9391 0.036
9644
G3 0.147
10017 0.110 10012 0.633
10005
G5 0.911
10007 0.531 10008 1.273
10004
G10 5.412
10006 2.860 10014 5.248
10006
G50 349.603
10018 56.67 10005 88.485
10006
Ra1 0.000
2650 0.000 494 0.00E+00
177
Ra2 0.073
9772 0.000 1111 0.00E+00
695
Ra3 0.593
10020 0.000 1867 0.239
4268
Ra5 2.951
10014 0.388 6300 2.688
9617
Ra10 19.720
10020 3.987 9417 9.830
10006
Ra50 149.98
10154 119.41 10076 114.50
10008
Ro1 0.000
18 6.46E-06 9832 5.56E-05
10008
Ro2 11.61
10013 5.32E-04 8259 3.56E-05
8474
Ro3 39.21
10010 0.111 10008 1.48
10008
Ro5 1.96E+04
10006 55.95 10012 116.87
10008
Ro10 3.29E+04
10011 1576 10026 9651
10008
Ro50 8.55E+07
10112 3.87E+05 10144 4.58E+07
10006
S62 1.07E-02
8746 5.05E-03 6822 3.69E-03
4807
S72 5.28E-02
7976 0.00E+00 780 0.00E+00
388
Studying results in Table 1 reveals that the
integer and decimal mutation operators have
successfully managed to improve the efficiency of
the algorithm either by decreasing the required
number of function evaluations or improving the
quality of the solutions or by resulting in both
improvements simultaneously. Using the integer and
decimal mutation operators in conjunction with
classical crossover and mutation operators resulted
in better fitness values in 93% of test cases and in
less required function evaluations in 74% of test
case. Furthermore, using integer and decimal
mutation operators in combination with the
crossover and mutation operator improved the
quality of the solution by at least 90% in 44% of test
cases.
The integer and decimal mutation operators
proved to outperform the classical crossover and
mutation operators in 78% of test cases in terms of
the quality of the solution and in 85% of test cases
in terms of required function evaluations. In 56% of
test cases the integer and decimal mutation operators
resulted in at least 50% of improvement in the
quality of solutions than the classical crossover and
mutation operators.
5 CONCLUSIONS
Two new genetic operators namely integer and
decimal mutation operators were proposed in this
paper. The operators were described and tested for
solving some classical minimization problems.
Furthermore, the efficiency of the proposed
operators against the classical crossover and
mutation operators was tested. Experimentation
proved that the proposed operators are efficient and
can lead into better results in solving optimization
problems.
REFERENCES
A. Eiben and J. Smith 2007. Introduction to Evolutionary
Computing. Natural Computing Series. Springer, 2nd
edition.
Bäck, Thomas, David B. Fogel, Darrell Whitely & Peter J.
Angeline 2000. Mutation operators. In: Evolutionary
Computation 1, Basic Algorithms and Operators. Eds
T. Bäck, D. B. Fogel & Z. Michalewicz. United
Kingdom: Institute of Physics Publishing Ltd, Bristol
and Philadelphia. ISBN 0750306645.
De Jong, K. A. 1975. An Analysis of the Behavior of a
Class of Genetic Adaptive Systems. Ph.D. thesis,
University of Michigan. Michigan: Ann Arbor.
Eshelman, L. J. & J. D. Schaffer 1991. Preventing
premature convergence in genetic algorithms by
preventing incest. In Proceedings of the Fourth
International Conference on Genetic Algorithms. Eds
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
190

R. K. Belew & L. B. Booker. San Mateo, CA: Morgan
Kaufmann Publishers.
G. Eiben and M. C. Schut 2008. New Ways To Calibrate
Evolutionary Algorithms. In Advances in
Metaheuristics for Hard Optimization, pages 153–177.
Holland, J. H. 1975. Adaptation in Natural and Artificial
Systems. Ann Arbor: MI: University of Michigan
Press.
Mengshoel, Ole J. & Goldberg, David E. 2008. The
crowding approach to niching in genetic algorithms.
Evolutionary Computation, Volume 16, Issue 3 (Fall
2008). ISSN:1063-6560.
Michalewicz, Zbigniew 2000. Introduction to search
operators. In Evolutionary Computation 1, Basic
Algorithms and Operators. Eds T. Bäck, D. B. Fogel
& Z. Michalewicz. United Kingdom: Institute of
Physics Publishing Ltd, Bristol and Philadelphia.
ISBN 0750306645.
Mitchell, Melanie 1998. An Introducton to Genetic
Algorithms. United States of America: A Bradford
Book. First MIT Press Paperback Edition.
Moghadampour, Ghodrat 2006. Genetic Algorithms,
Parameter Control and Function Optimization: A New
Approach. PhD dissertation. ACTA WASAENSIA
160, Vaasa, Finland. ISBN 952-476-140-8.
Mühlenbein, H. 1992. How genetic algorithms really
work: 1. mutation and hill-climbing. In: Parallel
Problem Solving from Nature 2. Eds R. Männer & B.
Manderick. North-Holland.
S. K. Smit and A. E. Eiben 2009. Comparing Parameter
Tuning Methods for Evolutionary Algorithms. In
IEEE Congress on Evolutionary Computation (CEC),
pages 399–406, May 2009.
Smith, R. E., S. Forrest & A. S. Perelson 1993. Population
diversity in an immune system model: implications for
genetic search. In Foundations of Genetic Algorithms
2. Ed. L. D. Whitely. Morgan Kaufmann.
Spears, W. M. 1993. Crossover or mutation? In:
Foundations of Genetic Algorithms 2. Ed. L. D.
Whitely. Morgan Kaufmann.
Ursem, Rasmus K. 2003. Models for Evolutionary
Algorithms and Their Applications in System
Identification and Control Optimization (PhD
Dissertation). A Dissertation Presented to the Faculty
of Science of the University of Aarhus in Partial
Fulfillment of the Requirements for the PhD Degree.
Department of Computer Science, University of
Aarhus, Denmark.
Whitley, Darrell 2000. Permutations. In Evolutionary
Computation 1, Basic Algorithms and Operators. Eds
T. Bäck, D. B. Fogel & Z. Michalewicz. United
Kingdom: Institute of Physics Publishing Ltd, Bristol
and Philadelphia. ISBN 0750306645.
SELF-ADAPTIVE INTEGER AND DECIMAL MUTATION OPERATORS FOR GENETIC ALGORITHMS
191
