
ULTRASONIC OFDM PULSE DETECTION FOR TIME OF FLIGHT
MEASUREMENT OVER WHITE GAUSSIAN NOISE CHANNEL
Daniel F. Albuquerque, Jos
´
e M. N. Vieira, Carlos A. C. Bastos and Paulo J. S. G. Ferreira
Signal Processing Lab – IEETA/DETI, University of Aveiro, 3810-193 Aveiro, Portugal
Keywords:
Pulse Detection, OFDM, Ultrasonic Location System.
Abstract:
In this paper we evaluate the probability of detection and the probability of false alarm for an OFDM pulse
over AWGN channel. This type of pulse is useful for indoor location systems using ultrasounds due to the
ability to accurately measure the time of flight by pulse detection while transmitting some data. Moreover, we
can avoid the RF auxiliary channel by using an OFDM-based sync. The probability of OFDM pulse detection
over white Gaussian noise will be presented as function of the probability of false alarm when a threshold
technique is employed at the receiver. Furthermore, the pulse detection probability will be compared with a
chirp pulse.
1 INTRODUCTION
Indoor location is an active area of research in the sig-
nal processing community with a large potential from
the point of view of applications (Sayed et al., 2005;
Liu et al., 2007). To perform indoor location, there are
2 main types of solutions: Ultrasonic (US) and Radio
Frequency (RF) based systems. RF power strength
based systems are inexpensive but require the profil-
ing of the entire location scenario to get a RF finger-
print resulting in an accuracy from 1 to 5 meters ap-
proximately (Stuntebeck et al., 2008; Bahl and Pad-
manabhan, 2000). On the other hand, the ultrasound
technology is the best suited to achieve the accuracy
required on indoor environments, that can be less than
1 cm in some cases (Gonzalez and Bleakley, 2009;
Prieto et al., 2007). Our location system, LocUS, aim
to be entirely based on ultrasound signals. Most of
the known ultrasonic location systems use an auxil-
iary RF channel for synchronization. An RF pulse is
used as a time reference for measuring the propaga-
tion delay between the source and the receiver (Hazas
and Hopper, 2006). Although this auxiliary RF chan-
nel allows very simple clock synchronization and de-
lay measurement solutions, it also gives away two im-
portant advantages that US-based systems bear in ref-
erence to RF-based ones: the immunity to RF interfer-
ence, and the ability to safely operate in the presence
of critical electronic instrumentation such as medical
or life-support systems. Therefore, one way to avoid
the use of an auxiliary RF signal to measure the time-
of-flight (TOF) is to synchronize the clocks of the
nodes (Skeie et al., 2001). To achieve this, the nodes
should be able to send to each other the clock infor-
mation using the ultrasonic channel. Due to the reflec-
tion of the ultrasonic signals on the walls the acoustic
communication channel presents a strong multipath
effect causing inter-symbolic interference.
LocUS solved this problem by using OFDM (Or-
thogonal Frequency Division Multiplexing) to per-
form data transmission. This technique has al-
ready been used in ultrasonic underwater communi-
cations (Mason et al., 2007; Nakashima et al., 2006).
OFDM is a very flexible modulation technique, robust
to multipath and that simplifies the channel equal-
ization. It is also very sensitive to synchronization,
which may be an advantage when the application re-
quires the measurement of the TOF (Levanon and
Mozeson, 2004). As we intend to send just one
OFDM data pulse with the carriers phase modulated,
to measure the phases we need to send another pulse
to measure the phases difference. That way, the first
pulse has a double purpose, it should have a high en-
ergy to be effectively detected by a matched filter and
it will be used as a phase reference by the second
pulse to decode the transmitted data.
In this paper it will be presented an analytical ex-
pression for the probability of OFDM pulses detec-
tion in the presence of white Gaussian noise. For
that propose it will be presented, in section 2, the
345
F. Albuquerque D., M. N. Vieira J., A. C. Bastos C. and J. S. G. Ferreira P..
ULTRASONIC OFDM PULSE DETECTION FOR TIME OF FLIGHT MEASUREMENT OVER WHITE GAUSSIAN NOISE CHANNEL.
DOI: 10.5220/0003375103450350
In Proceedings of the 1st International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2011), pages
345-350
ISBN: 978-989-8425-48-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
asynchronous data transmission with OFDM pulses.
In section 3 it is presented the probability of detec-
tion and the the probability of false alarm for OFDM
pulses over a white Gaussian noise channel when a
threshold technique is used in the receiver. Some sim-
ulation results will be presented in section 4. At the
end it will be presented a brief conclusion.
2 ASYNCHRONOUS DATA
TRANSMISSION WITH OFDM
An architecture for asynchronous data transmission
using OFDM pulses is proposed. We use two con-
catenated OFDM pulses, one for time synchroniza-
tion (e.g. time-of-flight measurement) and another for
some data information transmission (e.g. source iden-
tification). The group of the synchronization pulse
and the data information pulse is called frame.
2.1 Frame Prototype
Figure 1 presents the proposed frame prototype, as
mention before, there are two different main pulses in
the frame: The OFDM Sync. and the OFDM Data.
The first pulse is detected by the receiver by matched
filter and used to synchronization. It will also be used
to demodulate the second pulse, the OFDM Data, by
a differential demodulation scheme (Haykin, 2001).
This method was chosen manly because the OFDM
pulse is robust to environments with multipath but it
does not produce a very high resolution in time syn-
chronization, as will be seen later on. Therefore, the
differential demodulation will be robust to this small
jitter.
Guard
FFT
OFDM Sync.
Guard
Time
OFDM Data
Figure 1: Asynchronous data transmission with OFDM,
frame prototype.
The Guard FFT, presented in Figure 1 is a cyclic
extension to protect the demodulation process due to
the time synchronization jitter. The Guard Time is
a cyclic extension of the OFDM data pulse to avoid
inter-symbolic interference caused by the room im-
pulse response (Schulze and Luders, 2005).
3 OFDM PULSE DETECTION
Two different techniques to perform pulse detec-
tion can be used, the conventional time domain MF
(Matched Filter) or the FFT (Fast Fourier Transform)
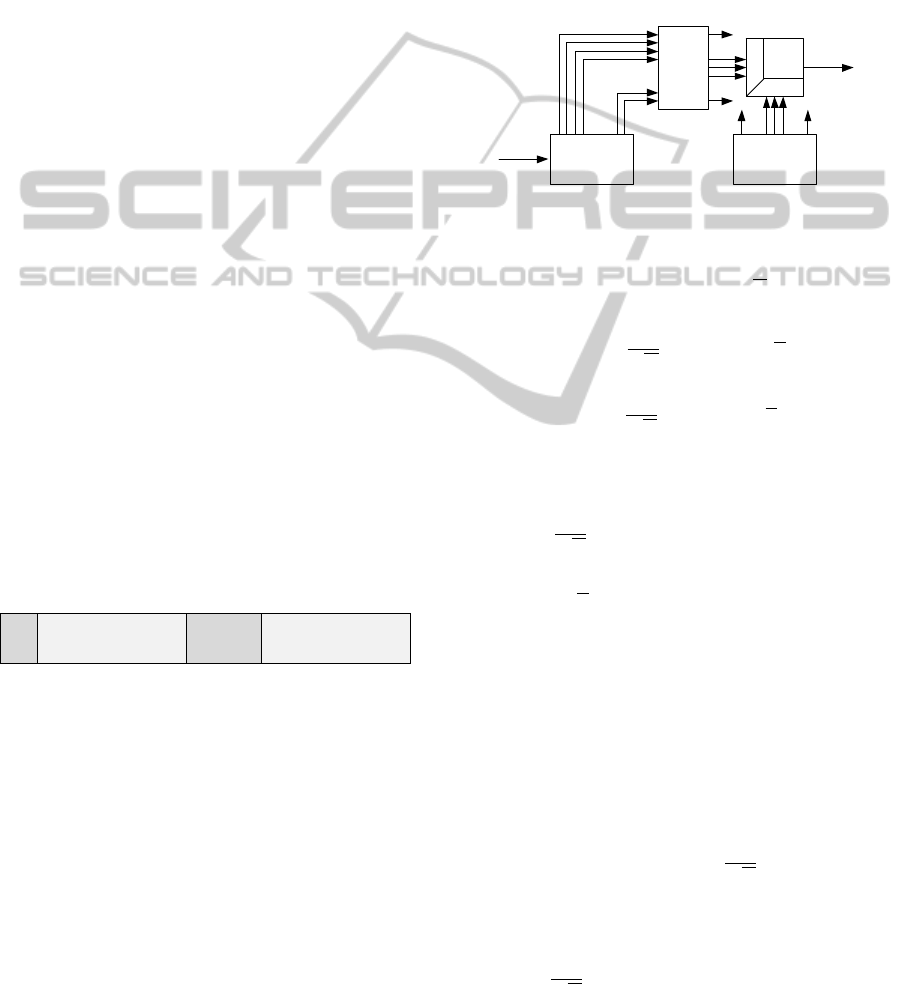
followed by a small scalar product. Figure 2 presents
the FFT technique, where the incoming signal, x
(pulse to detect plus noise) enters in a Buffer Delay
that has the same size of the pulse s. Therefore, the
information in the buffer is converted to the frequency
domain. Moreover, due to the OFDM properties S(k)
(Fourier transform of s) is only different from zero in
the information carriers so the system only needs to
perform the dot product in that carriers.
Delay
Buffer
FFT
...
S*(k)
a¢b
a
x(n)
y(n)
...
b
... ...
... ...
Figure 2: Pulse detection with FFT.
In the following sections is considered that the
FFT and IFFT are normalize to 1/
√
N:
X(k) =
1
√
N
N−1
∑
n=0
x(n)e
−j2π
nk
N
(1)
x(n) =
1
√
N
N−1
∑
k=0
X(k)e
j2π
nk
N
. (2)
Therefore, the output y
FFT
(n) of FFT detector can
be written as:
y
FFT
(n) =
1
√
N
N−1
∑
k=0
S
∗
(k)
N−1
∑
m=0
x(m + n −N + 1)W
−mk
.
(3)
where W = e
j
2π
N
and ()
∗
is the conjugate.
On the other hand, the output of the MF detector
y
MF
(n) is given by (Levanon and Mozeson, 2004):
y
MF
(n) =
N−1
∑
m=0
s
∗
(N −1 −m)x(n −m)
=
N−1
∑
m=0
x(m + n −N + 1)s
∗
(m)
(4)
where s(m) is the inverse Fourier transform of S(k):
y
MF
(n) =
N−1
∑
m=0
x(m+n−N +1)
1
√
N
N−1
∑
k=0
S(k)W
mk
!
∗
(5)
reorganizing the terms in the equation:
y
MF
(n) =
1
√
N
N−1
∑
k=0
S
∗
(k)
N−1
∑
m=0
x(m + n −N + 1)W
−mk
.
(6)
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
346

As can be seen, equation (6) is equal to equation (3).
In the FFT technique the scalar product has the
size of the number of carriers. On the other hand, the
MF technique needs to have a filter with the size of the
pulse. So the choice between one of these techniques
depends on the pulse size and the number of carri-
ers. If the pulse is small and there is a large number
of carriers, the MF is better than the FFT technique,
otherwise, if the pulse is big and there are only a few
carriers the FFT is better than the MF technique.
In order to simplify equation (6) and without loss
of generalization in the next section we will consider
the detector output with a time advance of (N −1)
y(n) =
1
√
N
N−1
∑
k=0
S
∗
(k)
N−1
∑
m=0
x(m + n)W
−mk
. (7)
3.1 Probability of Detection
In order the detect the presence of a pulse the output
y(n) must be compared to a given threshold. There-
fore, we consider that a pulse is detected if the output
y(n) is greater than the given threshold. Therefore,
the threshold must be chosen in a way that a very
weak pulse must be detected and the noise does not
produce false alarms. In this way, it is very impor-
tant to keep the probability of false alarm, which is
the probability of detecting the pulse when in the in-
put there is only noise, very small and the probability
of detection very high. To evaluate these probabilities
we must consider two competing hypotheses:
H
0
: x(n) = w(n)
H
1
: x(n) = w(n) + As(n)
(8)
which is equivalent to:
H
0
: x(n) = w(n) + As(n) , A = 0
H
1
: x(n) = w(n) + As(n) , A 6= 0
(9)
where H
0
is called the null hypothesis, H
1
the alter-
native hypothesis and w(n) is white Gaussian noise.
The system choose the hypothesis by the magnitude
of the signal y(n). Therefore, if the magnitude of y(n)
is greater than a given threshold γ the system decides
H
1
otherwise the system decides H
0
. This procedure
is shown in Figure 3.
> °
< °
jy(n)j
2
H
1
H
0
j j
2
y(n)
Figure 3: Detection decision block.
The output of the first block, after the compara-
tors, is given by:
|y(n)|
2
=
1
N
N−1
∑
k=0
S
∗
(k)
N−1
∑
m=0
x(m + n)W
−mk
2
(10)
Using (9):
|y(n)|
2
=
1
N
N−1
∑
k=0
S
∗
(k)
N−1
∑
m=0
w(m + n)W
−mk
+
+A
N−1
∑
m=0
s(m + n)W
−mk
!
2
(11)
The signal S(k) is only different from zero in a set
of carriers of the OFDM pulse, k ∈ (k
0
,k
1
,...,k
N
p
−1
)
(where N
p
is the number of OFDM pulse carriers),
they will be real due to the differential demodulation
and without loss of generalization we can consider
that |S(k)| = 1 for k ∈ (k
0
,k
1
,...,k
N
p
−1
). So we can
simplify the equation 11 to:
|y(n)|
2
=
1
N
k
N
p
−1
∑
k=k
0
S(k)
U
k
N
+ jV
k
N
!
+
A
k
N
p
−1
∑
k=k
0
S(k)
N−1
∑
m=0
s(m + n)W
−mk
2
(12)
where U(k/N) and V (k/N) for k = 1, 2,..., N/2 −
1 are random independent and Gaussian vari-
ables (Steven, 1993). Therefore, if w(m) is white
noise with zero mean and variance σ
2
, the U(k/N)
and V (k/N) also has zero mean and variance Nσ
2
/2.
Normalizing U and V to have unit variance, |y(n)|
2
becomes:
|y(n)|
2
=
N
p
σ
2
2
U(k/N)
p
Nσ
2
/2
+ j
V (k/N)
p
Nσ
2
/2
+ µ(n)
2
(13)
where µ(n) can be seen as the mean of the sum of this
two variables, moreover, it is dependent of the pulse
and it is only different from zero when the pulse is
present, µ(n)can be written as:
µ(n) =
A
σ
k
N
p
−1
∑
k=k
0
k
N
p
−1
∑
l=k
0
S(k)S(l)W
l(n−n
i
)
P(k −l, n)
N
p
N
p
/2
(14)
where n
i
is the first sample of the pulse and P(k,n) is
the Fourier transform of the boxcar function:
P(k, n) = W
−
(N−1+n
i
−n)k
2
ψ(k, n) (15)
ULTRASONIC OFDM PULSE DETECTION FOR TIME OF FLIGHT MEASUREMENT OVER WHITE GAUSSIAN
NOISE CHANNEL
347

where, for k 6= 0 ψ(k,n) is defined as:
ψ(k, n) =
sin
(N+n
i
−n)πk
N
sin
(
πk
N
)
n
i
≤ n < n
i
+ N
sin
(N+n−n
i
)πk
N
sin
(
πk
N
)
n
i
−N < n < n
i
0 otherwise.
(16)
Rewriting this equation, ψ(k, n) becomes:
ψ(k, n) =
sin
(n−n
i
)πk
N
sin
πk
N
(−1)
k
υ(n) (17)
were υ(n) is:
υ(n) = u(n −n
i
−1 + N) −2u(n −n
i
) +u(n −ni −N)
(18)
and u(n) is a unitary step (it is zero for n < 0 and one
otherwise). For k = 0, ψ(k, n) is defined as:
ψ(0,n) = Nυ(n)
2
+ (n −n
i
)υ(n) (19)
So the equation 14 can be simplified to:
µ(n) =
A
σ
k
N
p
−1
∑
k=k
0
k
N
p
−1
∑
l=k
0
S(k)S(l)W
(k+l)(n−n
i
)
2
ψ(k −l, n)
N
p
N
p
/2
(20)
Separating µ(n) in real and complex part it can be
written as:
µ(n) = µ
U
(n)+ jµ
V
(n) =
√
η
h
µ
0
U
(n)+ jµ
0
V
(n)
i
(21)
where η is:
η =
A
2
σ
2
. (22)
As S is real, µ
0
U
(n) and µ
0
V
(n) can be written sepa-
rately:
µ
0
U
(n) =
k
N
p
−1
∑
k=k
0
k
N
p
−1
∑
l=k
0
S(k)S(l)ψ
U
(k, l; n)
N
p
N
p
/2
(23)
µ
0
V
(n) =
k
N
p
−1
∑
k=k
0
k
N
p
−1
∑
l=k
0
S(k)S(l)ψ
V
(k, l; n)
N
p
N
p
/2
(24)
where ψ
U
(k, l; n) and ψ
V
(k, l; n) for k 6= l are defined
as:
ψ
U
(k, l; n) =
sin
2πl(n−n
i
)
N
−sin
2πk(n−n
i
)
N
2sin
π(k−l)
N
υ(n)
(25)
ψ
V
(k, l; n) =
cos
2πl(n−n
i
)
N
−cos
2πk(n−n
i
)
N
2sin
π(k−l)
N
υ(n)
(26)
for k = l ψ
U
(k, l; n) and ψ
V
(k, l; n) are defined as:
ψ
U
(l, l;n) = cos
2πl(n −n
i
)
N
ψ(0,n) (27)
ψ
V
(l, l;n) = −sin
2πl(n −n
i
)
N
ψ(0,n) (28)
Rewriting the equation 13, |y(n)|
2
becames:
|y(n)|
2
=
N
p
σ
2
2
"
U(k/N)
p
Nσ
2
/2
+ µ
U
(n)
!
2
+
+
V (k/N)
p
Nσ
2
/2
+ µ
V
(n)
!
2
#
(29)
The two quadratic terms in equation 29 can be
seen as a Chi-Squared distribution with two Gaussian
white independents variables (χ
0
2
2
(λ(n))) (Steven,
1993), one with µ
U
(n) mean and another with µ
V
(n)
mean. Where λ(n) is given by (Steven, 1993):
λ(n) = µ
U
(n)
2
+ µ
V
(n)
2
= ηλ(n)
0
(30)
where λ(n)
0
is given by:
λ(n)
0
= µ
0
U
(n)
2
+ µ
0
V
(n)
2
(31)
From equations 23, 24, 30 and 31 we can get two
important conclusions: First, the value of N does not
change the magnitude of λ
0
, second, λ is proportional
to η consequently λ is proportional to the signal to
noise ratio.
For the particular case when n = n
i
, (first sample
of the pulse), λ
0
takes the value 2N
p
so λ becomes:
λ(n
i
) = η2N
p
(32)
The Signal to Noise Ratio (SNR) is equal to
ηN
p
/N, therefore, λ can also be written in function
of the SNR and the size of the pulse:
λ(n
i
) = 2N ×SNR (33)
With these results it would be easy to compute the
probability of false alarm (P
f a
) and the probability of
detection (P
d
(n)) for any instant n.
The probability of false alarm can be seen as the
probability of choose H
1
when the system is in the
presence of H
0
i.e. the system believes to be in the
presence of the pulse but it only has noise in the input
(µ
U
(n) and µ
V
(n) are equal to zero). The probability
of false alarm can be defined as:
P
f a
= Pr
n
|y(n)|
2
> γ;H
0
o
(34)
Replacing |y(n)|
2
we obtain:
P
f a
= Pr
U(k/N)
√
Nσ/2
2
+
V (k/N)
√
Nσ/2
2
>
>
2γ
N
p
σ
2
;H
0
(35)
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
348

Therefore the probability of false alarm is:
P
f a
= Q
χ
0
2
2
(0)
2γ
N
p
σ
2
= Q
χ
2
2
2γ
N
p
σ
2
= e
−
γ
N
p
σ
2
(36)
where χ
2
2
represent a Chi-Squared distribution with
two Gaussian white independents variables with unit
variance and zero mean (Steven, 1993).
The probability of detection can be seen as the
probability of choosing H
1
when the system is in the
presence of the pulse i.e. the system considers that a
pulse was received and and one is present. The prob-
ability of detection can be defined as:
P
d
(n) = Pr
n
|y(n)|
2
> γ;H
1
o
(37)
Doing the same for P
d
that it was done for P
f a
P
d
(n) = Q
χ
0
2
2
λ(n)
2γ
N
p
σ
2
. (38)
Using (36) P
d
can be written as function of P
f a
P
d
(n) = Q
χ
0
2
2
λ(n)
ln(P
f a
−2
)
(39)
or
P
d
(n) = Q
χ
0
2
2
ηλ
0
(n)
ln(P
f a
−2
)
. (40)
4 RESULTS
In order to validate the theoretical detection probabil-
ity a test for a probability of false alarm of 10
−16
was
performed. In this test, it was considered the follow-
ing practical situation:
• An OFDM pulse with 17 carriers sampled at
100 kHz with the following amplitudes
S(k) = {1, 1,-1, -1,-1,-1,1,1, -1,1, 1,...
...-1,1,-1,1,-1,1}, k = k
0
.. .k
N
p
−1
;
• the lowest carrier frequency was set to 40 KHz
(k
0
= 400);
• the pulse has 1000 samples;
• the signal to noise ratio was set to 0 dB;
• for each sample 1000 simulations were per-
formed;
Figures 4 and 5 present the probability of detection
for a probability of false alarm of 1 ×10
−16
and 1 ×
10
−8
respectively. The horizontal axis represents the
incoming instant sample of the pulse with n
i
as the
instant when the last sample of the pulse was received.
Figure 4 shows that there is a great probability to
detect the pulse before the system receive the whole
ni−1000 ni ni+1000
0
0.5
1
P
d
Samp l e
expression
simulation
Figure 4: Probability of detection for a probability of false
alarm of the 1 ×10
−16
.
ni−1000 ni ni+1000
0
0.5
1
P
d
Samp l e
expression
simulation
Figure 5: Probability of detection for a probability of false
alarm of the 1 ×10
−8
.
pulse. Therefore, to improve the detection capabilities
we can use a very simple algorithm: When the system
detects a pulse it can wait for a period of time equal
to the length of the pulse and choose the maximum
value at the match filter output.
4.1 Comparison with other Usual Pulse
It was chosen a linear chirp also known as a linear
frequency-modulated pulse (Levanon and Mozeson,
2004) to compare with the proposed pulse. A lin-
ear chirp is a signal where its instantaneous frequency
change linearly with time. Moreover, this type of sig-
nals are usually used in radar and sonar systems (Lev-
anon and Mozeson, 2004).
For this test we chosen a chirp pulse with similar
characteristics (bandwidth, length, maximum ampli-
tude) to the OFDM pulse. The autocorrelation func-
tions of the OFDM and chirp pulses are shown in Fig-
ure 6.
−N 0 N
0
0.5
1
Sample
Amplitude
OFDM
Chirp
Figure 6: Comparison of the autocorrelation functions of a
chirp pulse and an OFDM pulse.
From Figure 6 it is possible to say that the Chirp
pulse is better for detection over noise environments
than the proposed OFDM pulse. Manly because it
ULTRASONIC OFDM PULSE DETECTION FOR TIME OF FLIGHT MEASUREMENT OVER WHITE GAUSSIAN
NOISE CHANNEL
349

produces a bigger amplitude in the matched filter out-
put. To prove this statement we evaluated the proba-
bility of detection as a function of the probability of
false alarm for 0 dB ratio of signal amplitude to noise
standard deviation. The results are presented in Fig-
ure 7.
10
−200
10
−150
10
−100
10
−50
10
0
0
0.2
0.4
0.6
0.8
1
P
fa
P
d
OFDM
Chirp
Figure 7: Probability of detection in function of probability
of false alarm.
5 CONCLUSIONS
In this paper we evaluated the probability of detection
of an OFDM pulse over white Gaussian noise chan-
nels for a given probability of false alarm. Therefore,
the resultant expression was validated with computer
simulations. The results demonstrated that the proba-
bility of detection of an OFDM pulse is lower than a
chirp with similar characteristics. This lower perfor-
mance comes from the reduced energy of the OFDM
compared to the chirp, this energy difference is due
to the amplitude concerns. However, this worst per-
formance does not compromise the potential for us-
ing OFDM pulses for asynchronous communication.
Simulation results have sown that if the probability of
false alarm is set to 10
−50
the pulse has a 90% prob-
ability of detection. Moreover, the proposed OFDM
pulse will be used not only for TOF measurements but
also for some data communication.
REFERENCES
Bahl, P. and Padmanabhan, V. N. (2000). RADAR: an in-
building RF-based user location and tracking system.
In Nineteenth Annual Joint Conference of the IEEE
Computer and Communications Societies, volume 2,
pages 775–784 vol.2.
Gonzalez, J. R. and Bleakley, C. J. (2009). High-Precision
Robust Broadband Ultrasonic Location and Orienta-
tion Estimation. IEEE Journal of Selected Topics in
Signal Processing, 3(5):832–844.
Haykin, S. (2001). Communication Systems. John Wiley &
Sons, 4th edition.
Hazas, M. and Hopper, A. (2006). Broadband ultrasonic lo-
cation systems for improved indoor positioning. IEEE
Transactions on Mobile Computing, 5(5):536–547.
Levanon, N. and Mozeson, E. (2004). Radar Signals. JOHN
WILEY & SONS.
Liu, J., Chu, M., and Reich, J. E. (2007). Multitarget Track-
ing in Distributed Sensor Networks. Signal Process-
ing Magazine, IEEE, 24(3):36–46.
Mason, S., Anstett, R., Anicette, N., and Zhou, S. (2007). A
Broadband Underwater Acoustic Modem Implemen-
tation Using Coherent OFDM. In The National Con-
ference On Undergraduate Research, California.
Nakashima, Y., Matsuoka, H., and Yoshimura, T. (2006).
Evaluation and Demonstration of Acoustic OFDM. In
Fortieth Asilomar Conference on Signals, Systems and
Computers, pages 1747–1751.
Prieto, J. C., Jimenez, A. R., and Guevara, J. I. (2007).
Subcentimeter-accuracy localization through broad-
band acoustic transducers. In IEEE International Sym-
posium on Intelligent Signal Processing, pages 1–6.
Sayed, A. H., Tarighat, A., and Khajehnouri, N. (2005).
Network-based wireless location: challenges faced
in developing techniques for accurate wireless loca-
tion information. Signal Processing Magazine, IEEE,
22(4):24–40.
Schulze, H. and Luders, C. (2005). Theory and Applica-
tions of OFDM and CDMA. John Wiley & Sons, first
edition.
Skeie, T., Johannessen, S., and Holmeide, O. (2001).
Highly accurate time synchronization over switched
Ethernet. In 8th IEEE International Conference
on Emerging Technologies and Factory Automation,
pages 195–204 vol.1.
Steven, M. K. (1993). Fundamentals of statistical signal
processing: estimation theory. Prentice-Hall, Inc.
Stuntebeck, E. P., Patel, S. N., Robertson, T., Reynolds,
M. S., and Abowd, G. D. (2008). Wideband powerline
positioning for indoor localization. In Proceedings of
the 10th international conference on Ubiquitous com-
puting, pages 94–103, Seoul, Korea. ACM.
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
350
