
LINE SEGMENT BASED STRUCTURE AND MOTION FROM TWO
VIEWS
A Practical Issue
Saleh Mosaddegh, David Fofi
Le2i, UMR CNRS 5158, Universit
´
e de Bourgogne, Le Creusot, France
Pascal Vasseur
MIS, Universit
´
e de Picardie Jules Verne, 33 Rue Saint Leu, 80039 Amiens, France
Keywords:
Motion estimation, Line segment correspondences, Two views, Optimization.
Abstract:
We present an efficient measure of overlap between two co-linear segments which considerably decreases the
overall computational time of a Segment-based motion estimation and reconstruction algorithm already exist
in literature. We also discuss the special cases where sparse sampling of the motion space for initialization of
the algorithm does not result in a good solution and suggest to use dense sampling instead to overcome the
problem. Finally, we demonstrate our work on two real data sets.
1 INTRODUCTION
Using lines for estimating motion is advantageous be-
cause they are easier to extract and have less localiza-
tion error than other features of interest such as points.
However, one can find several works in literature in
which the impossibility of motion determination from
the line correspondences between only two views are
mentioned (Zhang, 1995; Holt and Netravali, 1996;
Netravali and Huang, 2002; Faugeras, 2001). Clas-
sical methods such as (Taylor and Kriegman, 1995;
Bartoli and Sturm, 2005) which use supporting lines
(geometric abstraction of straight line segments) need
many line correspondences across at least three im-
ages. To our knowledge, the algorithm introduced
in (Zhang, 1995) is, so far, the only work based on
only two views which tries to recover motion and
structure by maximizing the total overlap of line seg-
ments in correspondence. In this paper we introduce
a unique and efficient way of computing overlap be-
tween two segments which considerably decreases the
overall computational time of this algorithm. We im-
prove the speed of proposed method by replacing its
objective function with a less computationally expen-
sive one without affecting the output of the algorithm.
For all our data sets in hand, it was also found that the
sampling strategy of the proposed method often is not
dense enough to obtain a good initial guess and one
need to sample the motion space with very small steps
to obtain an acceptable solution. On the other hand,
after densely sampling of the motion space, the best
initial guess is already enough close to the good so-
lution and further optimization does not improve the
estimation considerably. This observation also moti-
vated us to work on decreasing the time for calculat-
ing the objective function in order to be able to search
for a good solution over a densely sampled motion
space in a shorter time. The rest of this text is or-
ganized as follows. First a brief explanation of the
Zhang method as it is introduced in (Zhang, 1995). In
section 3 the new objective function is defined and its
performance compared to the previous function is dis-
cussed. The results in section 5 demonstrate how this
new function lead to a significant improvement in per-
formance in terms of execution time through applying
the method on a set of real data.
2 MOTION ESTIMATION BY
MAXIMIZING OVERLAPS
In this section, we present a brief summary of the al-
gorithm for solving the motion problem by maximiz-
ing the overlap of line segments introduced in(Zhang,
1995). The problem to be solved is that given the
680
Mosaddegh S., Fofi D. and Vasseur P..
LINE SEGMENT BASED STRUCTURE AND MOTION FROM TWO VIEWS - A Practical Issue.
DOI: 10.5220/0003357106800684
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 680-684
ISBN: 978-989-8425-47-8
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Overlap of two line segments in correspondence.
cameras intrinsic parameters and two sets of line seg-
ments, which are in correspondence, estimate the
camera extrinsic parameters (motion R and t).
Consider the pair of line segments(l, l
0
) in corre-
spondence as shown in Fig. 1. The line l
0
s
in the sec-
ond image is the epipolar line of end point s from the
first image, i.e. l
0
s
= E
e
s, where E = [t]
×
R is the essen-
tial matrix (Hartley and Zisserman, 2004).
e
s is the ray
which pass through end point s and center of first cam-
era and it can be easily computed since the camera
intrinsic parameters are assumed to be known. Sim-
ilarly the line l
0
e
is the epipolar line of the other end
point e. Taking cross product of each of these two
epipolar lines with the segment e
0
s
0
results in their in-
tersection, s” and e” with the segment. Provided that
the epipolar geometry (i.e. matrix E, or the motion
(R , t)) between two images is correct, then s and s”
correspond to a single point in space; so do e and e”.
Thus, the statement that two line segments l and l
0
share a common part of a 3D line segment is equiva-
lent to saying that line segment s”e” and line segment
s
0
e
0
(i.e.l
0
) overlap. The overlap length, L
0
, for two
line segments in correspondence can then be com-
puted from:
L
0
=
min(||e
0
− s
0
||,||e” − s
0
||,||e
0
− s”||,||e” − s”||)
i f
(s” − s
0
).(e
0
− s”) > 0
or (s” − s
0
).(e
0
− s”) > 0
or (s” − s
0
).(e
0
− s”) > 0
or (s” − s
0
).(e
0
− s”) > 0
−min(||e
0
− s”||,||e” − s
0
||)
otherwise
(1)
where . stands for dot product of two vectors. The
overlap length is positive if two line segments over-
lap, otherwise it is negative. We assume that the ori-
entation information of a line segment is not available
(i.e. the correspondence between end points of the
segments is not known). The overlap length in the
first image, denoted by L, can be computed exactly
in the same way . Since a small overlap length for a
short line segment is as important as a large overlap
length for a long line segment, we should use the rel-
ative overlap length, L
0
/||l
0
|| and L/||l|| to measure
the overlap of the pair of line segments. The relative
overlap length takes a value between 0 and 1 when
two segments overlap; otherwise it will be negative.
We define relative non-overlap length between two
corresponding segments l
i
and l
0
i
in the second image
as:
H
i
= (1 −
L
0
i
||l
0
i
||
) (2)
which is 0 when two segments completely overlap,
between 0 and 1 when they partially overlap and big-
ger than one when there is a gap between two seg-
ments. We can now formulate the motion problem as
estimating the camera motion parameters (R ; t) by
minimizing the following non-linear objective func-
tion:
F =
n
∑
i=1
(H
i
+ H
0
i
)
where n is the number of lines. The algorithm can be
summarized as the following pseudo-code:
Sample the rotation and the translation space with
sufficient steps.
for each sample R(i) in the rotation space do
for each t( j) in the translation space do
For hypothesized motion E = [t( j)]R(i) cal-
culate objective function F
0
=
n
∑
k=1
(H
k
+ H
0
k
)
end for
end for
for 10 best solution in matrix F
0
do
Using downhill simplex method, minimize F
starting with the best solution as initial guess.
end for
If sampling of motion space is with adequate small
steps, at least one of the ten minimization efforts in
the last loop converges to a good solution.
3 THE NEW MEASURE OF
OVERLAP
In above algorithm, H
0
(or H ), the function for com-
puting relative non-overlap length for each line cor-
respondence is the most frequently called function
and reducing computational time of this function can
largely decrease the overall computational time of the
algorithm. Consider the two possible configurations
of two collinear line segments as shown in Fig. 2.
The coordinates of two endpoints of the overlap part,
(Xmin,Y min) and (Xmax,Y max) can be found by:
X
min
= max(min(s
0
x
,e
0
x
), min(s”
x
,e”
x
)),
X
max
= min(max(s
0
,e
0
), max(s”
x
,e”
x
)),
LINE SEGMENT BASED STRUCTURE AND MOTION FROM TWO VIEWS - A Practical Issue
681
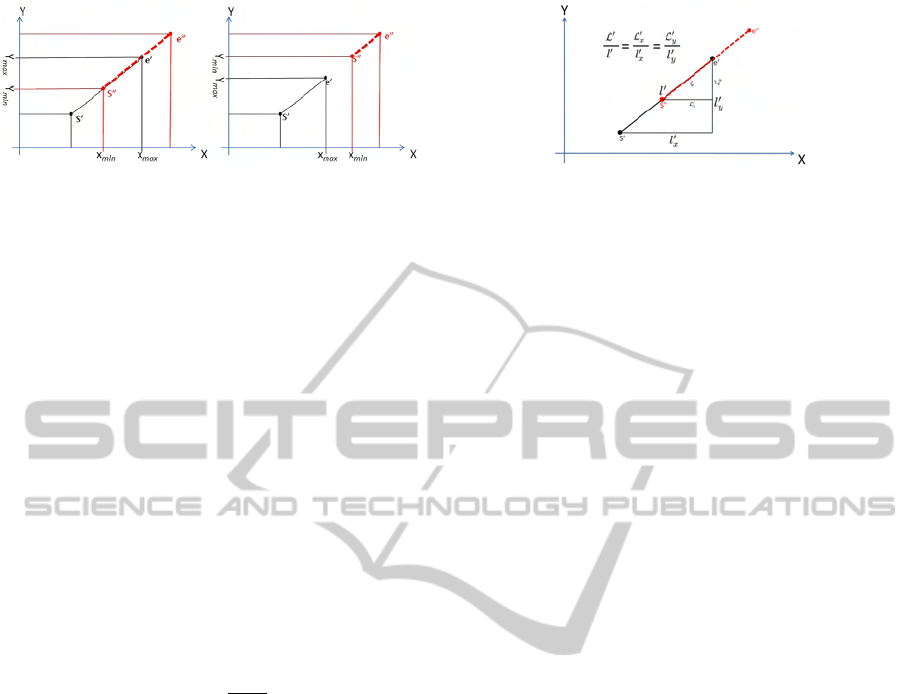
Figure 2: Two possible configurations of two collinear line
segments.
Y
min
= max(min(s
0
y
,e
0
y
), min(s”
y
,e”
y
)),
Y
max
= min(max(s
0
y
,e
0
y
), max(s”
y
,e”
y
)),
therefore, overlap length can be expressed by its
Cartesian length by:
L
0
i
= L
0
ix
+ L
0
iy
where
L
0
ix
= (X
max
− X
min
), L
0
iy
= (Y
max
−Y
min
)
Note that the output of this new measure of overlap
length is exactly equal to that of Equ. 1 but with-
out need for a i f − then construct with four OR con-
ditions. While computing the relative non-overlap
length, computational time can further be reduced by
half by considering only one of the Cartesian com-
ponents of the overlap part and the segment in the
second image (we chose x component) based on the
relation shown in Fig. 3:
H
i
= (1 −
L
0
ix
||l
0
ix
||
) (3)
However care should be taken when the segment
is vertical where y components should be used to
avoid undefined division 0/0. In order to have a very
accurate comparison between two measures, we care-
fully counted the number of CPU cycles needed to
run the assembly instructions for the new non-overlap
length measure as defined by Equ. 3 versus the mea-
sure defined by Equ. 2 compiled using a C com-
piler on an Intel Pentium machine. Our new non-
overlap length measure needs 302 clockticks (includ-
ing the conditional i f for proper treating of verti-
cal segments). The original measure of non-overlap
needs a minimum of 720 clockticks (if the first in-
equality condition among four inequalities in Equ. 1
is satisfied) and a maximum of 858 clockticks (if none
of four inequalities are satisfied). We can not use
clockticks average since for the majority of samples
in motion space and except for some random lines,
the rest of lines do not exhibit an overlap therefore the
computation of the objective function for these sam-
ples requires maximum number of clockticks. This
means our new measure can be computed on average
slightly less than 858/302 = 2.841 times faster than
Figure 3: The relation between Cartesian components of
the overlap part and the segment in the second image. The
ratios of corresponding sides of two right triangles are con-
stant.
the measure introduced in (Zhang, 1995), assuming
that the variation of the line segments is random. Re-
fer to the result section for a comparison using real
data.
4 RECOVERING MOTION BASED
ON DENSE SAMPLING
Sparse sampling of the 5 dimensional motion space
(3 for the rotation and 2 for the translation) followed
by refinement of the best samples as suggested in
(Zhang, 1995) is problem-in-hand dependent and de-
pending on how far the best initial guesses are to the
global minimum, the optimization stage can use con-
siderable iterations to converge to a good solution or
it may not be able to converge at all. Thanks to our
faster method for calculating the objective function,
we are able to sample the motion space more densely,
resulting in a better initial guess closer to the global
minimum with less time required by optimization al-
gorithm to converge to a good solution. The results in
the next section demonstrate how this new approach
can help to recover the motion for the examples where
the sparse sampling followed by a refinement of the
best samples cannot converge to a good solution.
5 RESULTS
We have already shown the efficiency of the new ob-
jective function in the terms of execution cycles. In
this section, however, we give the results on two real
data sets where for the last set the original algorithm
fails to recover the motion due to sparse sampling of
the motion space. The first set of real data is an image
pair of a bakery (Fig. 4). The position and rotation
of the second camera with respect to the first one was
obtained through a very careful setup and use of a gy-
roscope:
R = [−0.0073,−0.3049, −0.0036],
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
682
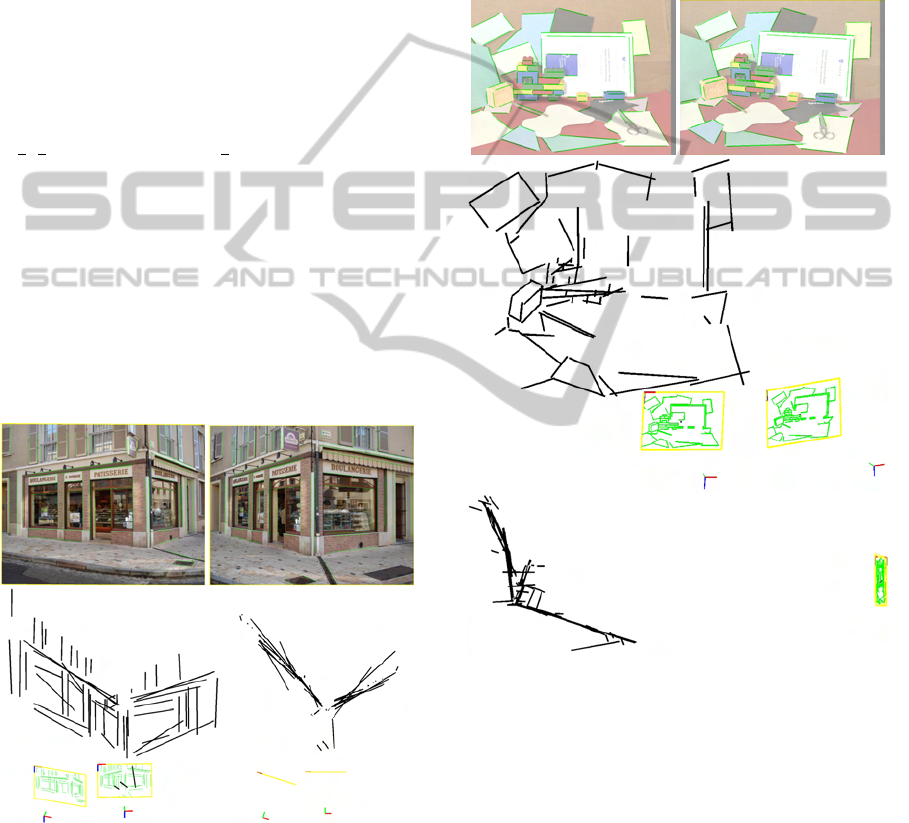
T
tra
= [0.9318,−0.0123, 0.3629],
where the translation T
tra
is normalized and the ro-
tation R is represented by a 3D vector whose direction
is that of the rotation axis and whose norm is equal to
the rotation angle. The segments which are aligned
with the epipolar lines are neglected during comput-
ing total overlap and later for the scene reconstruction
since in this case computed intersections, s and s” are
instable and the result overlap can be irrationally big,
resulting in eliminating a good solution.
For speed comparison, we applied the algorithm
with both original and new objective functions on this
data. We extracted and matched 85 lines between two
views manually. Through searching for the initial mo-
tion estimation by the sampling strategy as described
in the original algorithm (i.e. sampling the range
[−
π
4
,
π
4
] with steps equal to
π
8
for the rotation and 40
uniform sampling of a Gauss hemisphere based on
the icosahedron for the translation), only 1 of 10 best
samples converged to the good solution. The result of
the best solution is shown in Fig. 4. The whole pro-
cess (excluding the time for line extraction and match-
ing) took 3159 seconds composed of 1479 seconds
for evaluating the objective function over the motion
space and 1680 seconds for optimization of 10 best
initial guesses (both algorithm were implemented in
Matlab and were executed on the same computer).
Figure 4: Top row: Two images of a bakery with 85
matched line segments superimposed on the images (in
green) . Bottom row: 3D reconstruction of the bakery by
the structure from motion technique described in (Zhang,
1995). The right image corresponds to the top view.
Though replacing the function for computing rela-
tive non-overlap with our function does not alter the
output of the new algorithm, however it reduces the
overall computational time to 1215 seconds (around
2.6 times faster including all overhead computations).
The error in the translation direction is 1.0847
◦
. The
error in the rotation angle is 0.3087
◦
and the error in
the rotation axis is 1.9147
◦
.
Fig. 5 shows the second pair of images taken from
the real stereo image data set available at (INRIA, ).
The transformation from the first camera to the sec-
ond camera is:
Figure 5: Top row: A stereo pair with 104 matched line
segments superimposed on the images (in green) . Middle
row: A perspective view of the 3D reconstruction by classi-
cal stereo including two camera image planes. Bottom row:
a view from the side.
R = [−0.0004,0.3133, 0.0717],
T
tra
= [−0.9859,−0.0441, 0.1617],
We extracted and matched 104 lines between two
views manually. Through searching for the initial mo-
tion estimation by original sampling, none of the best
samples converged to a good solution. The best solu-
tion reconstruction corresponding to the initial guess
with the smallest value of objective function is shown
in Fig. 6.
As a matter of fact, this is an example of a scene
LINE SEGMENT BASED STRUCTURE AND MOTION FROM TWO VIEWS - A Practical Issue
683

Figure 6: 3D reconstruction of the scene by the best solution
of the structure from motion technique described in (Zhang,
1995). The bottom image corresponds to a side view. Ap-
parently this is not a good solution.
where it can be shown that the global minimum is
closely located to many local minima and only a fine
sampling of the motion space can result in a good
solution. Therefore we applied our dense sampling
strategy by 90 sampling of translation space and 1330
sampling of rotation space. The evaluation of the ob-
jective function for all these samples takes around
3120 seconds. The best solution’s reconstruction is
shown in Fig. 7. The error in the translation direc-
tion is 1.9
◦
. The error in the rotation angle and ro-
tation axis are 0.94
◦
and 1.986
◦
respectively. This
result is already very good and further optimization
is not necessary. One can notice that even though we
are benefiting from a faster objective function, how-
ever the evaluation of all samples in the dense motion
space is quite time consuming and except inevitable
evaluation of all these samples, there is not any other
deterministic alternative approach for such particular
examples.
6 CONCLUSIONS
We introduce a new measure of overlap which in-
creases the speed of the calculating the overlap be-
tween two line segments in correspondence. It also
allows a denser sampling of the motion space for find-
ing initial guesses for optimization of the non-linear
objective function for recovering motion based on line
segment correspondences and therefor facilitating the
search for a good solution where due to the nature
of the scene, sparse sampling followed by optimiza-
Figure 7: 3D reconstruction of the scene corresponding to
the sample with minimum value of objective function from
densely partitioned motion space.
tion does not converge to a good solution. We demon-
strated this situation by giving the results on two real
data sets including the scene where the original algo-
rithm fails to recover the motion.
REFERENCES
Bartoli, A. and Sturm, P. (2005). Structure-from-motion
using lines: Representation, triangulation, and bundle
adjustment. CVIU, 100(3):416–441.
Faugeras, O. (2001). Three-dimensional computer vision :
a geometric viewpoint. MIT Press, Cambridge, Mass.
Hartley, R. and Zisserman, A. (2004). Multiple View Geom-
etry in Computer Vision. Cambridge University Press.
Holt, R. and Netravali, A. (1996). Uniqueness of solutions
to structure and motion from combinations of point
and line correspondences. In JVCIR, volume 7, pages
126–136.
INRIA. Syntim stereo images. http://perso.lcpc.fr/
tarel.jean-philippe/syntim/paires.html.
Netravali, A. and Huang, T. (2002). Motion and structure
from feature correspondences: A review. In AIPU02,
pages 331–348.
Taylor, C. and Kriegman, D. (1995). Structure and mo-
tion from line segments in multiple images. PAMI,
17(11):1021–1032.
Zhang, Z. (1995). Estimating motion and structure from
correspondences of line segments between two per-
spective images. In ICCV95, pages 257–262.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
684
