
AFFINE SPHARM REGISTRATION
Neural Estimation of Affine Transformation in Spherical Domain
Valentina Pedoia, Ignazio Gallo and Elisabetta Binaghi
Dipartimento di Informatica e Comunicazione, Universit`a dell’Insubria, Varese, Italy
Keywords:
3D Surface registration, SPHARM registration, Affine transformation, RBF neural nework.
Abstract:
In this work we propose an algorithm to perform the affine 3D surface registration using the shape model-
ing based on SPHerical HARMonic: called SPHARM. In the existing SPHARM registration algorithms the
alignment is obtained using the rotation properties, that allows to perform the 3D surface rotation transforming
only the spherical coefficients. The major limit is that this approach aligns the surface only by rotation. We
propose a method to generalize this solution without lose the advantage to perform whole the registration pro-
cess in the spherical domain. An estimation of the coefficients transformation that guarantees an affinity in the
spatial domain is obtained by regression, using a set of RBF networks. The description of the 3D surface with
the spherical harmonic coefficients is brief but comprehensive and provides directly a metric of the shape sim-
ilarity. Therefore, the registration is obtained aligning the SPHARM model thought the minimization of the
root mean square distance between the coefficients vectors. Many experiments are performed to test the affine
SPHARM registration algorithm which appears efficient and effective compared with a standard registration
algorithm in the spatial domain.
1 INTRODUCTION
The 3D surface registration is dealt with extensively
in machine vision and computer graphics literature.
In the last few years a lot of techniques were pro-
posed (Xiao et al., 2005). Particular attention was
given on a parametric surface modeling. The most
widely used technique employs a description of a
radial or stellar surfaces v(θ, ϕ) with the spherical
harmonic decomposition (Ballard and Brown, 1982).
An extension of this work allows to describe more
general 3D simply connected surface using three
radial functions v(θ, ϕ) = x(θ, ϕ), y(θ, ϕ), z(θ, ϕ))
T
called SPHARM (SPHerical HARMonic modeling):
(Brechb¨uhler et al., 1995).
One of the most important field of application of
SPHARM is medical imaging, where a good regis-
tration allows to compare shapes from the patients
acquired in different moments, or different patients,
or a comparison with standard atlas. In this spe-
cific field an accurate and fast registration algorithm
is required. In most cases little transformations can
align two different anatomical surfaces, therefore ap-
proaches that solve efficiently and effectively the reg-
istration problem in this specific domain sacrificing
the generality are still well-regarded. The spheri-
cal harmonic domain lends itself well to perform the
3D surface registration. The reasons are the follow-
ing: the SPHARM allows a brief representation of
the 3D shapes and directly provides a shape descrip-
tor. Moreover, the correlation of the harmonic coef-
ficient’s degree and the level of detail of the descrip-
tion allows a hierarchical approach to the solution. Li
Shen (Shen et al., 2007) proposed a spherical surface
registration algorithm based on the minimization of
the root mean squared distance (RMSD) between two
SPHARM models. The major disadvantage is that
this approach solves the alignment problem only by
rotation, that is sufficient for shape analysis but not
enough for registration.
In this paper we present a novel method based on
neural networks for registration SPHARM model by
affine transformations. To obtain an analytical form
of the “affine transformation” of the coefficients is
an hard task. Indeed the orthogonality of the bases
is no longer guaranteed, hence the transformation of
each coefficient is function of all the other. Pro-
ceeding from these considerations a numerical ap-
proach based on neural network was chosen. The
registration is obtained through the minimization of
the root mean squared distance (RMSD) between two
SPHARM models by the Broyden-Fletcher-Goldfarb-
Shanno (BFGS) algorithm (Head and Zerner, 1985).
The whole registration process is developed in the
197
Pedoia V., Gallo I. and Binaghi E..
AFFINE SPHARM REGISTRATION - Neural Estimation of Affine Transformation in Spherical Domain.
DOI: 10.5220/0003318301970200
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 197-200
ISBN: 978-989-8425-47-8
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

spherical domain ensuring the algorithm efficiency.
The experimental results show a good regression ca-
pability of the network and a good level of gen-
eralization. The dimensionality reduction obtained
through the SPHARM modeling and the goodness of
the shape descriptor allow an efficient and effective
affine registration algorithm. The standard SPHARM
alignment algorithm and our extension of this work
to perform affine registration are described in the fol-
lowing.
2 SPHARM REGISTRATION
The aim of the SPHARM registration technique is the
use of the spherical parametrization of a 3D closed
surface for the description of the moving shape and
static template. Consider a 3D radial object repre-
sented by a set of vertices in the cartesian space v =
(x, y, z). The mapping of these vertices in the spherical
domain v(θ, ϕ) = ρ where θ ∈ [0, π] and ϕ ∈ [0, 2π] is
performed with surface parametrization (Floater and
Hormann, 2005). The spherical homogeneous sam-
pling of the space is obtained starting with an icosa-
hedron and iteratively subdividing each triangle into
four smaller triangles. A spherical surface can be de-
composed in a set of orthogonal bases through an in-
tegral transformation. The synthesis functions is the
following:
v(θ, ϕ) =
L
∑
l=0
l
∑
m=−l
c
m
l
Y
m
l
(θ, ϕ) (1)
SPHARM surface modeling of a radial object bene-
fits of the rotation property. The rotation of a sur-
face, defined trough the three Euler angles (α, β, γ)
can be compute directly in the spherical domain. If
the spherical function represents a radial object, the
coefficients rotation rotates, the parametrization and
also the object. The possibility to rotate a surface
only by rotating the harmonic expansion coefficients
makes the SPHARM alignment algorithms very effi-
cient but restricted only to the rigid transformations.
The spherical description of a surface is intrinsically
a metric of the shapes similarity. The surfaces align-
ment is obtained by aligning the SPHARM models
minimizing the root mean squared distance (RMSD)
between the harmonic coefficients.
RMSD =
v
u
u
t
1
4π
L
max
∑
l=0
l
∑
m=−l
||c
m
1,l
− c
m
2,l
||
2
(2)
3 AFFINE SPHARM
REGISTRATION
In this section our novel method is presented, aimed
to generalize the SPHARM registration algorithm for
affine transformations. To exploit the good features of
SPHARM modeling is necessary to perform the reg-
istration in the spherical domain. To this purpose, a
transformation of the spherical coefficients that guar-
antees an affine transformation in a space domain is
necessary. Instead of finding an analytical solution,
we attempt to solve the problem trough a Radial Ba-
sis Function (RBF) Neural Network. The affinity is
a class of linear transformations that maps variables
in new variables, it consists of a linear transformation
followed by a translation.
x
′
= Ax+t (3)
To find the affine transformation in the SPHARM
domain we start by considering, at first, only the
rotation: as shown by Li Shan, all the coefficients
c
m
l
(α, β, γ) of the rotated surface are a linear combi-
nation of all the coefficients of the same order and
lower degree.
c
m
l
(α, β, γ) =
l
∑
n=−l
D
l
mn
(α, β, γ)c
n
l
(4)
Observing that the affinity is a linear transformation
but don’t preserve the orthogonality of the basis we
can suppose that all the coefficients c
m
l
(a) of the sur-
face after affine transformation are a linear combina-
tion of all the other coefficients.
c
m
l
(a) =
L
′
∑
k=0
k
∑
n=−k
T
lk
mn
(a)c
n
k
(5)
The analytical definition of the function T
kl
nm
(a) is a
critical aspect and is not guaranteed a closed-form
expression. To asses this problem the RBF net-
works were introduced to regress this function. One
of the easiest and effective way to model regression
is that of using a finite dimensional space of func-
tion spanned by a given basis. The RBF neural net-
work solves the regression problem by this way with
a very simple structure and, differently from other
types of neural network, like Multy Layer Percep-
tron (MLP), with a faster training (Buhmann and Buh-
mann, 2003). Moreover, the RBF works well if is
trained with many examples, as will be shown be-
low, in this specific application, the ground truth set
can be arbitrarily large. For each c
m
l
(a) one RBF
network is involved. As mentioned above the gen-
eration of the training set is easy: let be v
′
(θ, ϕ) the
surface v(θ, ϕ) after the affine transformation A(a)
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
198

we can extract the c
m
l
of the original surface and the
c
m
l
(a) of the transformed surface. The input pat-
tern of the RBF network approximates the c
m
l
(a) is
[a
1
, ...a
12
, c
0
0
, c
−
1
1
, c
1
0
, c
1
1
....c
l
l
, c
l
l
]. The training set is
composed of a series of affine transformations of the
same object, the network can generalize only in the
domain of the training shape and the affine transfor-
mations of this. Depending to the training set the net-
work can be specialized to a particular affine deforma-
tions (scaling shearing,reflection...). The alignment
process is performed, like in the SPHARM registra-
tion by Li Shen , minimizing the root mean squared
distance (RMSD) between the harmonic coefficients
(Eq. 2).
4 EXPERIMENT RESULTS
Several experiments, to asses the capability of the pro-
posed method and to find the best network tuning are
performed. Once we have established the best net-
work configuration in terms of number of radial basis
function and training cardinality, the performance are
evaluated for the two steps:
• the performance of the neural estimation of affine
transformation of coefficients: that involve the
network capability to regress the function and
generalize.
• the performance of affine SPHARM registration:
that include the goodness of the SPHARM shape
descriptor and the capability of the minimization
algorithm to find the affine transformation that
best aligns the 3D surfaces. Our algorithm is
compared with a classical registration algorithm:
Demon registration (Kroon and Slump, 2009) in
terms of RMSE and execution time.
The networks are trained on 750 examples of affine
transformation with scaling (s
x
, s
y
, s
z
) from 0.8 to 1.2,
shearing (s
hxy
, s
hxz
, s
hyx
, s
hyz
, s
hzx
, s
hzy
) from -0.2 to 0.2
and rotation angles (α, β, γ) from −
π
10
to
π
10
. The
RMSE is computed between the surface transformed
in space domain trough the application of the affine
matrix and performing a bicubic interpolation and
the surface obtained transforming the spherical coeffi-
cients with the network and reconstruction the surface
with the synthesis equation (Eq. 1). The networks
performance are tested, with the K-fold technique (10
experiments). In Figure 1 the results of one of the K-
fold experiment is shown for the training and test set,
the mean of RMSE is 0.95 for the first and 1.16 for
the second. As expected the performances are better
for the training set but not so considerably, that is a
symptom of a good generalization.
50 100 150 200 250
0
1
2
3
Experiments
RMSE (mm)
RBF Affine transformation of Spherical Coefficients − Test Set
Transformation Error
Mean = 1.1623
100 200 300 400 500 600 700
0
1
2
3
Experiments
RMSE (mm)
RBF Affine transformation of Spherical Coefficients − Training Set
Transformation Error
Mean = 0.95315
Figure 1: Neural estimation of affine coefficients transfor-
mation performance on training set and test set.
The performance of the Affine SPHARM regis-
tration are evaluated through the comparison with
a standard registration algorithm the ”MRI Modal-
ity transformation in Demon Registration” proposed
by Kroon and Slump. The algorithm is based on
a Thirlon Demon Registration (Thirion, 1998). The
experiments are performed with different types of
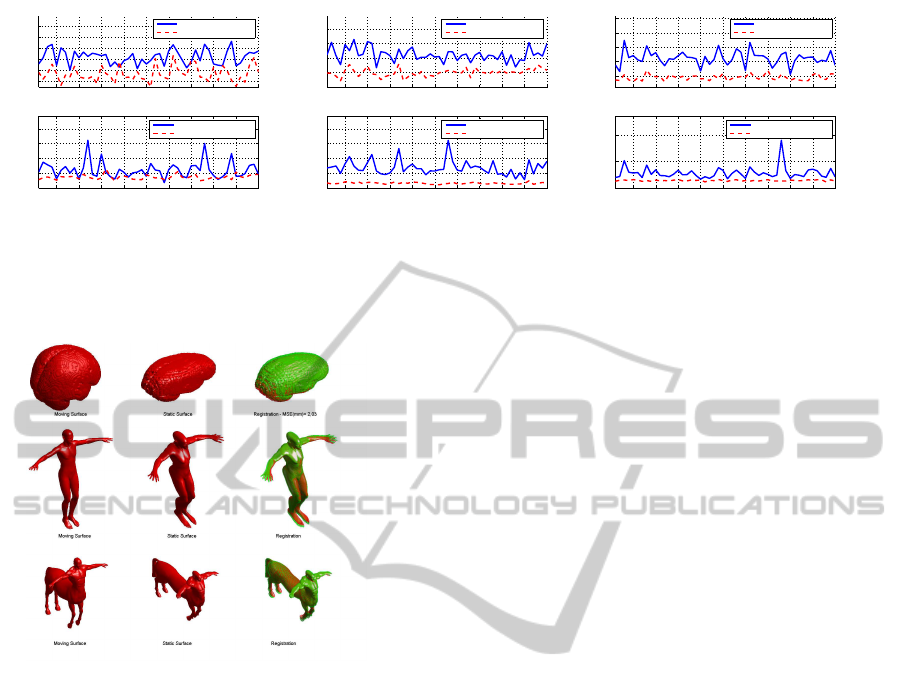
affine transformations: scaling and rotation Figure
2(a), scaling and shearing 2(b), and a general affine
transformation 2(c). The performance are evaluated
in term of RMSE and execution time. Note, the data
used are randomly chosen in the test set.
Observing the mean of the registration error the
good performance of the affine SPHARM registration
is clear. The RMSE means in these experiments are
always lower for our algorithm rather the demon reg-
istration. Moreover, differently to the Demon Regis-
tration the affine SPHARM performances appear in-
variant to the type of transformation.
In Figure 3 examples of surfaces alignment per-
formed by the affine SPHARM registration are
shown. In the three cases the RBF networks are
trained with examples of the specific shape and affine
transformations of these. These examples show how
the performance are good also with more complex
shape. Both the second and third examples belong
to TOSCA data set (Toolbox for Surface Comparison
and Analysis) (A. M. Bronstein, 2008):”david” and
”centaur”.
5 CONCLUSIONS
In this paper we propose an innovative method
to solve the 3D surface registration based on the
SHARM modeling. The results show good perfor-
mance of the neural approach for the estimation of the
coefficients transformation. The chosen RBF network
allows a fast and easy training phase. Moreover the
possibility of creating an arbitrary large training set
AFFINE SPHARM REGISTRATION - Neural Estimation of Affine Transformation in Spherical Domain
199
5 10 15 20 25 30 35 40 45 50
2
4
6
8
10
12
Experiment
RMSE (mm)
Brain Data Set − Scaling And Rotation Affine Transform
Demon, Mean: 6.4338
SPHARM, Mean: 3.3772
5 10 15 20 25 30 35 40 45 50
0
20
40
60
80
Experiments
Matlab Time (s)
Demon, Mean: 24.3298
SPHARM, Mean: 14.5796
5 10 15 20 25 30 35 40 45 50
0
5
10
15
20
Experiments
RMSE (mm)
Brain Data Set − Scaling And Shearing Affine Transform
Demon, Mean: 11.121
SPHARM, Mean: 4.9678
5 10 15 20 25 30 35 40 45 50
0
20
40
60
80
Experiments
Matlab Time (s)
Demon, Mean: 27.4018
SPHARM, Mean: 6.3784
(a)
5 10 15 20 25 30 35 40 45 50
5
10
15
20
25
Experiments
RMSE (mm)
Brain Data Set − General Affine Transform
Demon, Mean: 11.1269
SPHARM, Mean: 4.3949
5 10 15 20 25 30 35 40 45 50
0
50
100
Experiments
Matlab Time (s)
Demon, Mean: 28.4175
SPHARM, Mean: 14.0552
(b)
Figure 2: Performance comparison between Affine SPHARM Registration and Demon Registration in terms of registration
error end execution time for different affinity class: (a) Scaling and Rotation (6 D.O.F.), Scaling and Shearing (9 D.O.F.),
General Affinity (12 D.O.F.).
Figure 3: Examples of Surface registration: in the first col-
umn the moving surfaces, in the second the static surfaces
and in the third the superposition of the static surfaces (red)
and the registered surfaces (green) are shown.
or specializing it to a particular set of transformation,
makes our approach very attractive. The experimen-
tal results shown good performance of the algorithm
in terms of execution time and registration error for
little deformation while the affine SPHARM perfor-
mances worse in cases of big deformation. This prob-
lem is imputable to the loss of the basis orthogonality
thought the affinity transform. In our future works we
want to establish a theoretical limit to application of
the affine SPHARM, and a method to solve this limi-
tation.
REFERENCES
A. M. Bronstein, M. M. Bronstein, R. K. (2008). Numerical
geometry of non-rigid shapes. Springer.
Ballard, D. H. and Brown, C. M. (1982). Computer Vision.
Prentice-Hall, Englewood Cliffs, N.J.
Brechb¨uhler, C., Gerig, G., and K¨ubler, O. (1995).
Parametrization of closed surfaces for 3-d shape de-
scription. Comput. Vis. Image Underst., 61(2):154–
170.
Buhmann, M. D. and Buhmann, M. D. (2003). Radial Basis
Functions. Cambridge University Press, New York,
NY, USA.
Floater, M. S. and Hormann, K. (2005). Surface parameter-
ization: a tutorial and survey.
Head, J. D. and Zerner, M. C. (1985). A broyden–fletcher–
goldfarb–shanno optimization procedure for molecu-
lar geometries. Chemical Physics Letters, 122(3):264
– 270.
Kroon, D.-J. and Slump, C. H. (2009). Mri modalitiy trans-
formation in demon registration. In ISBI’09: Proceed-
ings of the Sixth IEEE international conference on
Symposium on Biomedical Imaging, pages 963–966,
Piscataway, NJ, USA. IEEE Press.
Shen, L., Huang, H., Makedon, F., and Saykin, A. J. (2007).
Efficient registration of 3d spharm surfaces. In CRV
’07: Proceedings of the Fourth Canadian Conference
on Computer and Robot Vision, pages 81–88, Wash-
ington, DC, USA. IEEE Computer Society.
Thirion, J. P. (1998). Image matching as a diffusion process:
an analogy with maxwell’s demons. Medical Image
Analysis, 2(3):243–260.
Xiao, G., Ong, S. H., and Foong, K. W. C. (2005). Effi-
cient partial-surface registration for 3d objects. Com-
put. Vis. Image Underst., 98(2):271–294.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
200
