
DISPERSION EFFECT ON GENERALISATION ERROR
IN CLASSIFICATION
Experimental Proof and Practical Algorithm
Beno
ˆ
ıt Gandar
1,2
, Ga
¨
elle Loosli
1
1
Clermont Universit
´
e, Universit
´
e Blaise Pascal, 63000 Clermont-Ferrand, France
and CNRS, UMR 6158, LIMOS, 63 173 Aubi
`
ere, France
Guillaume Deffuant
2
2
Cemagref de Clermont-Ferrand, Laboratoire LISC, 24 avenue des Landais, 63 172 Aubi
`
ere Cedex 1, France
Keywords:
Machine Learning, Classification, Space Filling Design, Dispersion.
Abstract:
Recent theoretical work proposes criteria of dispersion to generate learning points. The aim of this paper is
to convince the reader, with experimental proofs, that dispersion is a good criterion in practice for generating
learning points for classification problems. Problem of generating learning points consists then in generating
points with the lowest dispersion. As a consequence, we present low dispersion algorithms existing in the
literature, analyze them and propose a new algorithm.
1 INTRODUCTION
In the context of classification tasks, we address the
question of optimal position of points in the feature
space in the case one as to define a given number of
training points anywhere in the space. Those train-
ing points will be named sequence from now on. To
that purpose, we want to use the dispersion of the se-
quence, which is an estimator of the spread. The dis-
persion is defined in the next section as well as ref-
erences to a paper stating that this criterion is likely
to be more efficient for classification tasks than other
well known criteria such as discrepancy. Our point
in this position paper is to convince the reader that a)
the dispersion is in practice a good criterion and b)
we can provide an efficient algorithm to use it, even
though evaluating this dispersion is costly.
2 DEFINITION OF DISPERSION
Dispersion is an estimator of the spread of a sequence
used in numerical optimization. It is usually used
in iterative algorithms in order to approximate the
extremum of a non derivable function in a compact
set. The error approximation can also be theoretically
expressed by a function of dispersion (Niederreiter,
1992).
Dispersion of a Sequence: Let I
s
be the unit cube in
dimension s with the euclidian distance d. The dis-
persion of a sequence x =
{
x
1
,...,x
n
}
is defined by:
δ(x) = sup
y∈I
s
min
i=1,...,n
d(y,x
i
)
Figure 1: Estimation of dispersion. The dispersion is the
radius of the largest ball containing no point.
The dispersion of a sequence is the radius of the
largest empty ball of I
s
(see Figure 1).
Bounds of Dispersion of a Sequence: (Niederre-
iter, 1992) shows that dispersion of a sequence x =
{
x
1
,...,x
n
}
in I
s
is lower bounded by:
δ(x) ≥
1
2
b
s
√
n
c
. (1)
Moreover, he proves that for each dimension s, it ex-
703
Gandar B., Loosli G. and Deffuant G..
DISPERSION EFFECT ON GENERALISATION ERROR IN CLASSIFICATION - Experimental Proof and Practical Algorithm.
DOI: 10.5220/0003293007030706
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 703-706
ISBN: 978-989-8425-40-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
ists a sequence x in I
s
such:
lim
n→+∞
s
√
nδ(x) =
1
log(4)
.
As a consequence, for each dimension s, it exists a
sequence x in I
s
such δ(x) = O
1
s
√
n
. Considering
previous inequality, this order is the lowest.
3 EXPERIMENTAL EVIDENCE
In order to illustrate theoretical results and to observe
the effects of decreasing dispersion of training points,
we present experiments involving the following three
steps:
1. Learning with k-NN from random samples of
fixed size for different classification functions,
and estimating the generalization error.
2. Then we decrease the sequence dispersion by run-
ning a few iterations of the algorithm described in
section 4. We apply the classification algorithm
using these new samples and estimate the gener-
alization error. This step is repeated until the dis-
persion algorithm stops.
3. Finally, we represent the generalization error rate
depending on the dispersion rate (decreasing)
with boxes and whiskers. Note that the disper-
sion is observed on sequences and is not a param-
eter. Each box has lines at the lower quartile, me-
dian, and upper quartile values. Whiskers extend
from each end of the box to the adjacent values in
the data. The most extreme values are within 1.5
times the interquartile range from both end of the
box. Adjacent values represent 86.6% of popula-
tion for a gaussian distribution.
We have generated two types of classification rules in
spaces of dimension 2 to 5:
• The first type of rules is relative to simple classi-
fication problems. The classification boundaries
have small variations and are smooth.
• The second type of rules is relative to difficult
classification problems. Classification bound-
aries have more important variations and are less
smooth. Moreover classifications surfaces have
more connected components.
Experimental Protocol: We have made experiments
with 2000 learning points and 5000 test points on 500
learning problems, in space of dimension 2 to 5. The
results are similar in all tested dimensions, and we
report here for dimension 5 in Figures 2 and 3.
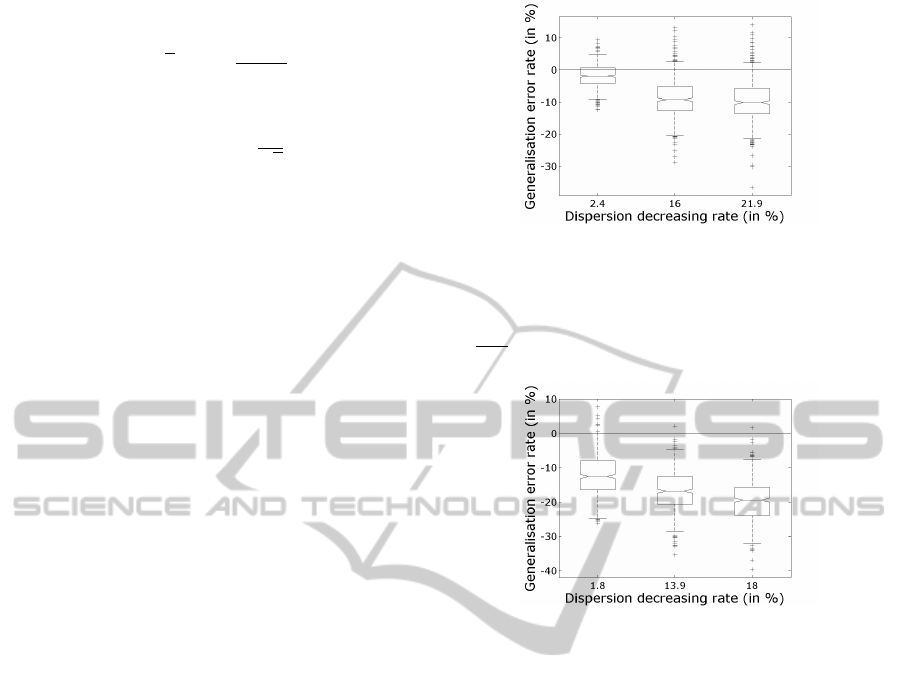
Figure 2: Relative decrease of generalization error vary-
ing with the relative decrease of dispersion for 500 sim-
ple learning problems in dimension 5 with 2000 learning
points. (if δ
i
is the initial dispersion and δ
t
the dispersion
after several iterations of the algorithm, the relative decrease
is
δ
i
−δ
t
δ
i
). The boxes represent distribution of error rates.
Figure 3: Relative decrease of generalization error varying
with the relative decrease of dispersion for 500 hard learn-
ing problems in dimension 5 with 2000 learning points.
Conclusion and Discussion: We can see that lines of
median value (middle lines of boxes) are below zero
in the majority of problems. It shows that decreasing
dispersion reduces error generalization in more than
50% of cases. We can also remark that the higher
the dispersion decrease, the lower the generalization
error rate. Upper liners of boxes (they represent 75%
of population) are also below zero once dispersion
minimizing algorithm has converged. Moreover it
seems that more complex learning problems are,
more k-NN algorithm is sensitive to dispersion of
learning points.
4 LOW DISPERSION
ALGORITHMS
In this part, we look for generating a sequence with
the lowest dispersion as possible for a fixed size. Pi-
oneering works of (Johnson et al., 1990) about gener-
ation of low dispersion sequences proposed two dif-
ferent criteria: a criterion to minimize called minimax
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
704

and a criterion to maximize called maximin. In a first
part, we present in first criterion of minimax and al-
gorithms based on it. In a second part, we present
criterion of maximin and also algorithms based on it.
In each part, we explain why different algorithms pre-
sented are not optimal.
4.1 Minimax
Minimax criterion based algorithms try to minimize
the maximal distance between points of the sequence
and candidate points.
Algorithms based on Swaping Points Process:
(Johnson et al., 1990) have proposed an algorithm
which makes the reduction of minimax criterion by
a simple swap of points, starting from random. The
convergence of the algorithm is guaranteed, but no
guarantee is given to have generated the best possi-
ble sequence.
Algorithms based on Adding Points Process:
(Lindemann and LaValle, 2004) have developed an
incremental algorithm reducing dispersion of se-
quences by adding points. They reduce also disper-
sion and get around the initial global problem of min-
imization. However, this method reduces incremen-
tally the dispersion by adding points and is not op-
timal when the user has a fixed maximal number of
points.
4.2 Maximin
An alternative to minimizing the dispersion consists
in maximizing the distance between the points of
the sequence. It is easier to optimize numerically
and corresponds to the maximin criterion defined by
δ
2
(x) = inf
(x
1
,x
2
)∈I
s
2
d(x
1
,x
2
). We can once more distin-
guish two types of algorithms: Algorithms based on
Deleting Points Process: (Sergent et al., 1997) have
proposed to generate a sequence with a lot of points
and to delete superfluous points until we obtain a se-
quence with a fixed minimal distance between points.
The major disadvantage of this algorithm is the quasi-
impossibility to predict the size of the final sequence.
Algorithms based on Adding Points Process: It is
also possible to generate a low dispersion sequence
by adding points to an initial sequence according to
maximin criterion where the dispersion is high . How-
ever the algorithms based on maximisation of δ
2
(x) =
inf
(x
1
,x
2
)∈x
2
d(x
1
,x
2
) push generally points towards the
frontier of cube. This effect can be avoided by con-
sidering the criterion δ
3
(x) = inf
(x
1
,x
2
)∈x
2
d(x
1
,{x
2
}∪I
s
0
)
where I
s
0
=
{
x ∈R
s
|x /∈ I
s
}
. A set which maximizes
δ
3
(x) is also said a maximin set. Being inspired by
works of (Lindemann and LaValle, 2004), (Teytaud
et al., 2007) have developed an algorithm based on
criterion δ
3
(x) and random trees to explore the space.
At first step, they generate a point in the middle of unit
cube. Then, at each step, they add a point with maxi-
mization of criterion δ
3
(x). As a consequence, adding
this point is optimum toward the previous space con-
figuration. However the obtained configuration is not
necessarily the best one with this total number of
points.
To Summarize. All theses methods are not op-
timal and we have to considers the total number of
points to generate low dispersion sequence: it is the
purpose of the next part.
5 A NEW LOW DISPERSION
ALGORITHM
We propose an algorithm using the properties of dis-
persion established by (Niederreiter, 1992), and based
on maximin criterion together with spring variables.
Those spring variables are function of the distance
between the points of the sequence and between the
points and the borders of unit cube. This algorithm
has good properties in practice: for an appropriate
number of points, it converges to the Shukarrev grid
which minimizes dispersion and it converges gener-
ally quickly. Its complexity is about O
n
2
k
for a
sequence of size n and k iterations.
Sketch of the Algorithm: The basic idea of
the algorithm is to achieve two tasks : spread the
points as much as possible and remain inside the unit
cube and not too close to the boundaries (similarly to
Shukkarev grids). Hence we have defined two steps,
each dealing with one of the tasks. The algorithm it-
erates over those steps until convergence. In practice,
we also have to deal with some local minima (leading
to oscillations) and the stopping criteria.
Description of Each Step:
Initialization. We generate randomly a sequence
S with n points preferably in the middle of the unit
cube, S =
{
x
i
}
i=1,...,n
in dimension s. At each step,
each point pushes away its neighbors that are closer
that d
m
=
1
b
s
√
n
c
. Indeed, we know from inequality
(1), that δ(S) ≥ d
m
.
Spreading the Points. For each point x of S,
we only consider as neighbors the points x
i
of S
with distance inferior to d
m
. We compute a spring
variable between x and each neighbor x
i
defined by
DISPERSION EFFECT ON GENERALISATION ERROR IN CLASSIFICATION - Experimental Proof and Practical
Algorithm
705

2 ∗d
m
−d(x,x
i
)
2 ∗d
m
p
. Parameter p is a positive inte-
ger and we have observed experimentally that p = 4
is satisfactory. With p = 4, the value of the spring
variable varies from 1/16 (further points) to 1 (nearest
points). Then, we move point x proportionally to each
spring variable into the direction of vector x −x
i
: the
closer the points are, the more the algorithm spaces
them. Moreover proportionality used is decreasing in
time until a threshold value, from which it becomes
constant.
This process is similar to the minimax approach and
pushes the points outside of the unit cube. Problem
of generating a low dispersion sequence consists then
in a minimization criteria with box constraints. We
apply also these contraints: cube’s borders are repul-
sive in the direction of cube’s center, depending on
the distance between these points and borders.
Applying box Constraints. In order to keep points
inside the hypercube, we apply a repulsive force on
points near borders. These points are detected with
one of their coordinates which is inferior to
d
m
2
+ ε
m
or superior to 1 −
d
m
2
−ε
m
: these values are the coor-
dinates of extremum points of a Sukharev grid with
a tolerance about ε
m
=
d
m
4
. Intensity of this force
has the same proprieties as forces used in step called
Spreading the points. Globally, we perform a local
dispersion minimization which becomes global after
iterating this process.
Avoiding Configuration with Local Minimum. Ap-
plying iteratively these two previous steps can lead to
local minimum and oscillations : a high number of
points can be aligned on the edge. Repulsive forces
push points on the same direction with the same in-
tensity and the trend to push points outside hypercube
at the step called Spreading the points nullifies the ac-
tion of repulsive forces. There are then oscillations of
these points. In order to avoid development of theses
local minimum configurations, after a few number of
iterations, we select randomly a point on each borders
in each dimension and change their coordinate along
these dimensions to a random value near the middle
of cube.
Stopping Criteria: Different stopping criteria
can be used to end the iterations: a maximal num-
ber of iterations, the stabilization of the dispersion or
a minimum threshold on the average changes of the
points during one iteration. This point still requires
some further exploration.
6 CONCLUSIONS
In this paper, we illustrate experimentally the theoret-
ical result established by (Gandar et al., 2009), show-
ing that dispersion is probably a pertinent criterion
for generating samples for classification and we deal
with the question of generating the best low disper-
sion samples. We provide a quite simple algorithm
able to minimize the dispersion for a fixed size se-
quence.In experimental design, grids are usually used
to select sets of parameters for experiments. How-
ever, using grids imposes hard limits to the number
of parameters that can be explored (often less than 6).
We believe that being able to efficiently generate low
dispersion sequences can help in this context, since
the number of points can be fixed to any value and in
any dimension (obviously, the number of points has
be realistic depending on the dimension). In active
learning, the learning algorithm has to select which
training point will be used (implying that its label is
asked for, which has a cost). Most of times, the train-
ing points pre-exist but it happens that one can ask for
any point in the space. In that particular case, given
a limited budget for labels (which provides the max-
imum number of training points), the proposed algo-
rithm could be directly applied. Concerning the se-
lection task, our algorithm can be adapted to be able
to select an existing point nearby the ideal position.
This is our future work.
REFERENCES
Gandar, B., Loosli, G., and Deffuant, G. (2009). How to op-
timize sample in active learning : Dispersion, an opti-
mum criterion for classification ? In European confer-
ence ENBIS European Network for Business and In-
dustrial Statistics.
Johnson, M., Moore, L., and Ylvisaker, D. (1990). Mimi-
max and maximin distance designs. Journal of Statis-
tical Planning Inference, 26(2):131–148.
Lindemann, S. and LaValle, S. (2004). Incrementally
Reducing Dispersion by Increasing Voronoi Bias in
RRTs. In IEEE International Conference on Robotics
and Automation.
Niederreiter, H. (1992). Random Number Generation and
Quasi-Monte Carlo Methods. Society for Industrial
and Applied Mathematics.
Sergent, M., Phan Tan Luu, R., and Elguero, J. (1997). Sta-
tistical Analysis of Solvent Scales. Anales de Quim-
ica, 93(Part. 1):3–6.
Teytaud, O., Gelly, S., and Mary, J. (2007). Active learning
in regression, with application to stochastic dynamic
programming. In Proceedings of International Con-
ference on Informatics to Control, Automation and
Robotics.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
706
