
AN ASYNCHRONOUS MULTI-AGENT SYSTEM
FOR OPTIMIZING SEMI-PARAMETRIC SPATIAL
AUTOREGRESSIVE MODELS
Matthias Koch and Tamás Krisztin
Vienna University of Economics and Business, Institute for Economic Geography and GIScience, Vienna, Austria
Keywords: Agent-based modelling, Asynchronous teams, ATeams, Semi-parametric spatial autoregressive modelling,
Evolutionary algorithms.
Abstract: Classical spatial autoregressive models share the same weakness as the classical linear regression models,
namely it is not possible to estimate non-linear relationships between the dependent and independent
variables. In the case of classical linear regression a semi-parametric approach can be used to address this
issue. Therefore we propose an advanced semi-parametric modelling approach for spatial autoregressive
models. Advanced semi-parametric modelling requires determining the best configuration of independent
variable vectors, number of spline-knots and their positions. To solve this combinatorial optimization
problem we propose an asynchronous multi-agent system based on genetic-algorithms. Three teams of
agents work each on a subset of the problem and cooperate through sharing their most optimal solutions.
Through this system we can derive more complex relationships, which are better suited for the often large
and non-linear real-world problems faced by applied spatial econometricians.
1 INTRODUCTION
Spatial autoregressive (SAR) models have seen a
wide approach in dealing with empirical problems.
The key difference between a classical regression
and a spatial model is that the latter incorporates a so
called spatial lag of the dependent variable. Both
model classes assume that the impact of the
independent variables on the depended variable can
be modelled in a linear fashion. This might not be
true in many applied cases. Therefore, the linear
regression model was extended by the semi-
parametric regression models. These semi-
parametric regression models are able to cope with
most kind of nonlinearity [see for example Fahrmeir
et al]. As a result, we want to extend the SAR-
models by semi-parametric modelling techniques.
Our suggested semi-parametric spatial
autoregressive (SPSAR) estimation-method is based
on so called truncated-splines (for details see
Fahrmeir et al., 2009, page 296) and Akaike
Information Criteria (AIC) minimization. The
truncated spline and the spatial autoregressive
estimators will be calculated via a maximum
likelihood (ML). In order to model complex
nonlinear relationships between the dependent and
independent variables we will first choose suitable
combinations of the independent variables and use
them to as argument for the truncated splines. The
truncated spline has an optimized number and
position of knots. Therefore, we are partly faced
with a combinatorial optimization problem.
In the first section of the paper we will
introduce asynchronous multi-agent systems and
discuss their characteristics and why they are well-
suited for solving the combinatorial optimization
problem at hand. The next section details the
nonlinear spatial autoregressive models, the SPSAR
estimation method and the nature of the optimization
problem. The third section outlines the asynchronous
agent architecture, while the fourth section
introduces our proposed testing methodology.
2 ASYNCHRONOUS
MULTI-AGENT SYSTEMS
This section provides a brief introduction to agents,
multi-agent systems (MAS) and a more specific
483
Koch M. and Krisztin T..
AN ASYNCHRONOUS MULTI-AGENT SYSTEM FOR OPTIMIZING SEMI-PARAMETRIC SPATIAL AUTOREGRESSIVE MODELS.
DOI: 10.5220/0003292704830486
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 483-486
ISBN: 978-989-8425-41-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
overview of asynchronous MAS for solving large
combinatorial optimization problems.
The definition of agents is laid down by
Jennings and Wooldridge (1995), namely an agent is
defined by possessing one or more of the four
characteristics:
• Autonomy is the agent’s ability to work
without human interaction and have a
control of their own state and actions.
• Social ability is the ability to communicate
with other agents.
• Reactivity denotes the ability to respond to
actions and to perceive the environment.
• Pro-Activeness is the agent’s ability to
work towards a goal and take initiative in
actions.
A multi-agent system is a collection of loosely
coupled agents, who cooperate to solve a problem
(Sycara, 1998). In an MAS each agent has only
limited information and problem solving capacity, so
that the posed problem can only be solved through
cooperation. Furthermore there is no central entity
that manages the system, instead data and problem-
solving are decentralized and managed by individual
agents.
Asynchronous problem-solving teams
(ATeams), have been proposed by Talukdar et al.
(1998). They are a form of MAS, where the system-
wide current best solutions of a problem are stored
in a central memory. Problem-solving agents try to
generate more optimal solutions, each agent with
another problem-solving algorithm, while destroyer
agents are deleting sub-optimal solutions from the
central memory. The architecture of such an ATeam
is asynchronous, agents act in an autonomous way
and they exchange information through the shared
memory.
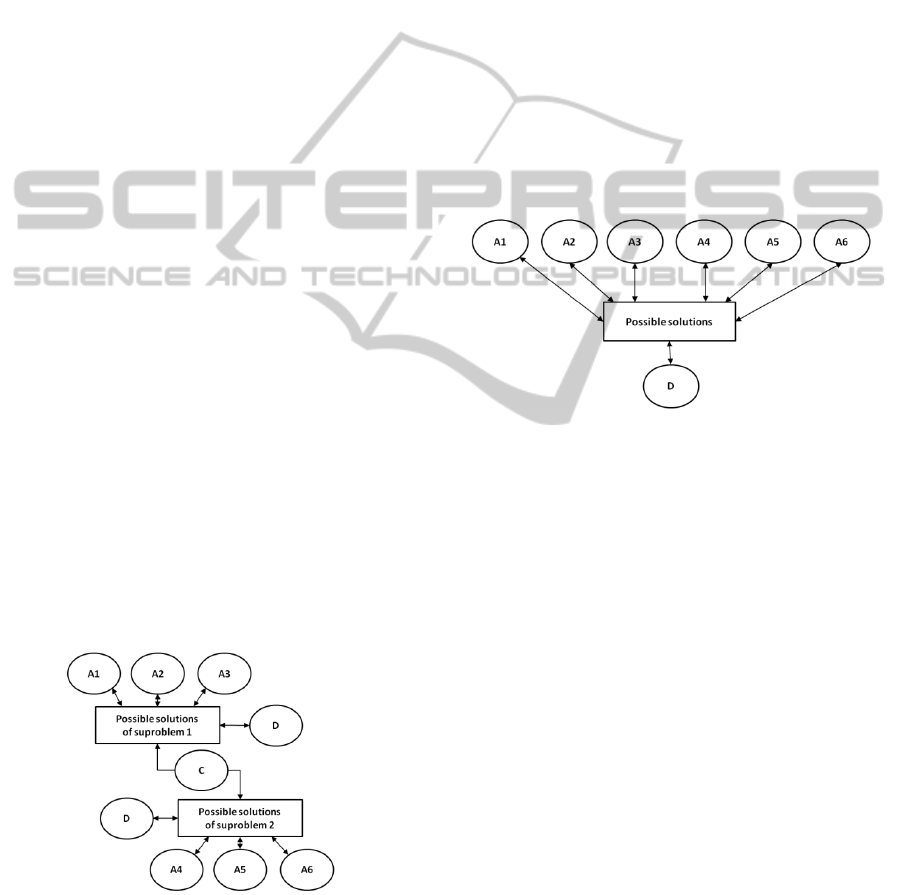
Figure 1: Multiple ATeams cooperating on subsets of a
problem.
Fig 1 illustrates this principle, where agents A1
through A6 are working to solve the problem using
algorithms a1 through a6. They add their most
optimal solutions to the solution population in the
memory M. Other agents review these solutions
periodically and try to come up with more optimal
solutions. The destroyer agent D is checking the
population of solutions and deletes any inferior
solution which is below a threshold t.
For more complicated problems, multiple
ATeams can be employed, with each team of agents
working on a subset of a problem. Communication
between the teams depends on the organization of
the problem and by what degree the subsets of the
problem depend on each other. Fig. 2 shows two
agent teams, the first team is A1 through A3 and the
second team A4 through A6, cooperating in this way.
The second team of agents builds on the population
of the first and an coordinator agent C provides
subproblems for the second team from the solutions
of the first team.
Figure 2: Architecture of an ATeam.
In some sense ATeams are similar to
blackboard systems, where problem-solvers
cooperate by posting the results of their calculations
on a blackboard. In ATeams though the agents
operate independently and unlike in blackboard
systems, there is no central instance of control and
agents work independently from each other (Aydin
et al., 2004).
It is possible to combine ATeams with
evolutionary methods, such as genetic algorithms.
This can be done either with each agent as an
instance of an algorithm or each agent performing
the individual steps of the algorithm. In such a case
one agent would implement the population selection,
while others implement crossovers and genetic
mutations. It is easy to implement hybrid methods,
with different evolutionary algorithms, in an
ATeam, since agents can be easily added or
substracted from the system; this offers a flexible
way of solving complex optimization problems
through addition of different selection and crossover
methods (Aydin et al., 2004).
Talukdar et al. (1998) used the well-known
shortest path problem as a benchmark for ATeams.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
484

By applying this methodology to the problem they
demonstrated that the solutions provided by ATeams
offer more reachability and can solve the problem in
a more efficient manner, than more conventional
methods. Other applications of similarly structured
asynchronous MAS can be found in the supply-chain
literature (Kazemi et al. 2007. Aydin et al. 2004)
where they are still popular. We are not aware of any
other applications of ATeams in the field applied
spatial econometrics.
3 NONLINEAR
AND SEMI-PARAMETRIC
SPATIAL AUTOREGRESSIVE
MODELS
This section introduces nonlinear spatial
econometric models and then suggests semi-
parametric modelling to account for the nonlinearity.
Since this paper focuses primarily on the
asynchronous multi Agent systems, this section
should only be seen as a sketch for the actual
SPSAR-econometric problem.
We consider the following nonlinear spatial
autoregressive model (1):
=
+
,
,…,
,
+
where
~.
0,
(1)
In (1)
is a n by 1 vector containing the dependent
variable.
is a n by k matrix of observations on k
independent variables,
is a n by n spatial
weighting matrix of known constants, ρ is the spatial
autoregressive parameter and
is an independently
normal distributed random vector with zero mean
and
variance.
,
,…,
,
is a nonlinear
continuous function with continuous derivatives
form ℝ
×
→ℝ
×
. Additionally we assume that
only contains metric variables. For notational
simplicity we ignore in this section the constant term
of the spatial regression model.
We assume that
is either row or maximum
row standardized and that the true parameter of is
smaller one in absolute value. Therefore, we can
solve (1) for
and get (2)
=
−
,
,…,
,
+
−
(2)
Since we do not know the specific form
,
,…,
,
we first use a finite truncated
Taylorseries. Since this series is not practicable, we
use a series of truncated splines
,
of optimized length m, where
is the set
containing the optimized knots for the truncated
spline and
∈
,
⨀
,
|
j,o
∈ Τ
×Τ
,
l,h
∈ Τ
×
Τ
∪
,
,…,
,
|j∈ Τ
where Τ
=
1,2,…,x
. Hence
,
,…,
,
will be approximated by
∑
,
. Since
,
represents a
truncated spline,
∑
,
must have a linear
representation:
∑
,
=
̅ for given
vectors
, the set
and the length m. If we use
this approximation of
,
,…,
,
we can
rewrite (2) to (3)
≈
+
̅
+
(3)
Estimators for , ̅ and
(we will denote
estimators with ^) in (3) can be found via ML. ML
leads to the following maximization problem (4) (Le
Sage and Pace, 2009):
=
,
,
1
2π
det
exp −
1
2σ
−
̅
′
−
̅
(4)
where
=
−
. With the estimators ,
and
we are able to calculate the AIC. We
consider
a good estimator for
,
,…,
,
if we find a minimal AIC. Since most of the
econometric issues like ML are already sufficiently
solved, the next section discusses the optimization
procedure for finding optimal
and number and
position of the truncated spline knots.
4 SOLUTION METHODOLOGY
To optimize the problem of semi-parametric spatial
autoregressive models, which we introduced in the
previous section, we propose three asynchronous
teams of agents, each working on a subset of the
optimization. The first team attempts to optimize the
number of splines, the second team adjusts the
position of the spline-knots, while the third team
tries to find the optimal variable vectors for the
selected number of splines and positions. A
coordinator agent is responsible for informing the
other teams about the current most optimal results of
the three problem subsets. Based on the AIC of these
results, each team of agents attempts to improve
upon the solution. A destroyer agent deletes in each
AN ASYNCHRONOUS MULTI-AGENT SYSTEM FOR OPTIMIZING SEMI-PARAMETRIC SPATIAL
AUTOREGRESSIVE MODELS
485

cycle the worst solution from each of the three
populations.
The system starts with a pool of randomly
selected population samples, with uniform
distribution. Each team consists of three agents.
These agents encapsulate the selection, crossover
and mutation of genetic algorithms. They deposit the
new samples into a population pool, shared by all
three agents. The agents differ in the crossover
methods, which are applied to the members of the
population. The three agent teams use the same three
genetic algorithms. The termination criteria for the
system is either 1000 cycles or the system terminates
when no change has been detected in either of
optimal solutions of the agent teams, for the last 20
cycles.
Each agent implements the following steps:
1. The first step is the evaluation of the
current solution population, according to
the AIC criteria.
2. In the second step a subset of individuals
are selected from the population, for
producing a new generation of solutions.
This is done through roulette wheel
selection for all agents.
3. The offspring are created by recombining
elements of their parents and by mutation.
The mutation is done throughout all agent
types by stochastical perturbation for the
newly created generation.
4. In the final step, the new generation is
inserted into the population.
As mentioned 3previously, there are three types of
agents in the system; each of them uses different
crossover methods:
• The first type of agent (g1) uses single-
point crossover for creating new solutions,
• the second agent type (g2) employs two-
point crossover and
• the third type of agents (g3) uses a random
crossover method, whereby a binary
random vector - corresponding to the length
of the first parent - is created. Where the
vector has a value of 1, the matching value
of the first parent is chosen, else the
equivalent value of the second parent is
selected for the offspring.
The communication agent selects in each cycle the
best solution – determined by the AIC value – from
each of the three ATeams and informs the other
ATeams about the parameters of this selection.
5 CONCLUSIONS
This paper derives an optimization for semi-
parametric spatial autoregressive models, through
asynchronous multi-agent teams. The agent teams
employ genetic algorithms and cooperate to find the
optimal solution for this large combinatorial
optimization problem.
This agent-based model offers an elegant
method for applied spatial econometrics. Through
combined agent teams the problem can be
subdivided and solved on separate levels. In addition
it is also possible to try other then evolutionary
methods for the agents, even combining hybrid
approaches. Due to the characteristics of ATeams
such an extension can be implemented to utilise the
proposed methodology for other spatial econometric
problems.
REFERENCES
Aydin, E. M., Fogarty, T. C., 2004. Teams of autonomous
agents for job-shop scheduling problems: an
experimental study. Journal of Intelligent
Manufacturing, 15, 455-462.
Fahrmeier, L., Kneib, T., Lang, S., 2009. Regression:
Modelle, Methoden und Anwendungen. Springer,
Berlin/Heidelberg/New York.
LeSage, J., Pace, R. K., 2009. An introduction to spatial
econometrics. Tylor & Francis Group, Boca
Raton/London/New York.
Kazemi, A., Fazel Zarandi, M. H., Moattar Husseini, S. M.
2007. A multi-agent system to solve the production-
distribution planning problem for a supply-chain: a
genetic algorithm approach. International Journal of
Advanced Manufacturing Technology, 44, 180-193.
Sycara, K. P., 1998. Multiagent systems. Artificial
Intelligence Magazine, 19(2), 79-92.
Talukdar, S., Baerentzen, L., Gove, A., De Souza, P.,
1998. Asynchronous teams: cooperation schemes for
autonomous agents. Journal of Heuristics, 4(4), 295—
321.
Wooldridge, M., Jennings, N. R., 1995. Intelligent agents:
theory and practice. Knowledge Engineering Review,
10, 115-152.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
486
