
DECISION MAKING BASED ON DUALITY BETWEEN POSITIVE
AND NEGATIVE EVALUATIONS
Rumiko Azuma
Graduate School of Engineering and Science, University of the Ryukyus, Nishihara, Japan
Hayao Miyagi, Yui Miyagi
Faculty of Engineering, University of the Ryukyus, Nishihara, Japan
Keywords:
Decision-making, Dual hierarchy, Reachability.
Abstract:
This paper proposes a model of dual hierarchy to study a decision-making structure with positive and negative.
It is necessary to evaluate a decision in negative stand point, such as insufficient, hatred, pressure, as a cause
of fraud, as well as positive evaluation. In order to treat the positive and negative elements, we propose a
model of dual hierarchy process which can evaluate from positive and negative points. Moreover, a technique
to judge a consistency of dual evaluation is presented, using a concept of reachability matrix.
1 INTRODUCTION
On the decision-making problem under risk environ-
ment, it is important subjects how a risk is quantified
and modeled. There is a fraud as one of the risks that
exist in the company organization etc., and it appears
as the serious problem.
AHP(Analytic Hierarchy Process) proposed by
Saaty (T.L.Saaty, 1980) is one of the decision-making
method which evaluates human’s subjective feeling.
AHP for risk management (Azuma and Miyagi, 2009)
is a research treating the risk in the decision mak-
ing problem. In the research, degree of satisfaction
is regarded as positive utility, and degree of risk is
regarded as negative utility. It is based on positive
decision-making same as existing methods because
negative utility depends on statistical data. However,
in fraud prevention assessment, it is necessary to eval-
uate a decision in negative stand point, such as insuf-
ficient, hatred, pressure, as a cause of fraud, as well
as positive evaluation.
In this paper, in order to solve this problem,
we discuss a development of decision-making model
which can be analyze the human’s double psychology
in fraud prevention.
2 DUALITY IN ORDER
RELATION
In decision-making process, there are some cases that
decision maker can not allow a rational and logical
consistent evaluation. As an example, there is the
deadlock in a three-cornered tie, and that is the order
relation of preferences is uncertain. Such discrepancy
can be discovered by calculating consistency index.
However, if the order relation is not the deadlock in
a three-cornered tie, it is difficult to discover a dis-
crepancy. To discover the discrepancy in decision-
maker, it is the one of way to check a fraud action. In
the present study, in order to develop a new approach
to discover a discrepancy under the human’s subcon-
scious, we focus on the duality relation of order as
follows:
When the elements of the ordered set X = x
i
satis-
fies the following three rules, the set X has the former
theorem p, at the same time, it has new theorem p
∗
that replaced all relations of order.
• x ≤ x (reflexivity)
• If x ≤ y and y ≤ x then x = yiasymmetryj
• If x ≤ y and y ≤ z then x ≤ zitransitivityj
This concept is the duality theorem (Ataka, 1966).
That is, p
∗
is the duality theorem of p. In this paper,
we propose the procedure that the discrepancy gener-
685
Azuma R., Miyagi H. and Miyagi Y..
DECISION MAKING BASED ON DUALITY BETWEEN POSITIVE AND NEGATIVE EVALUATIONS.
DOI: 10.5220/0003287006850688
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 685-688
ISBN: 978-989-8425-40-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
ated in the decision-making process can be shown by
utilizing the concept.
3 DUAL STRUCTURED
DECISION-MAKING MODEL
Existing decision making system is type of selecting
superiority. However, it is not easy to deal with nega-
tive elements such as ”pressure”, ”recognition of op-
portunity” and ”self-justification” which may appear
in fraud problem. In particular, ”pressure” and ”self-
justification” influence psychological factor of deci-
sion maker.
Then, we propose inferiority decision procedure
on opposite point of superiority in order to treat hu-
man’s negative psychology. We believe there is a
close relationship between superiority model and in-
feriority model because they are in the relation of
the flip side. In the present study, we discuss both
decision-making mechanism and propose the model
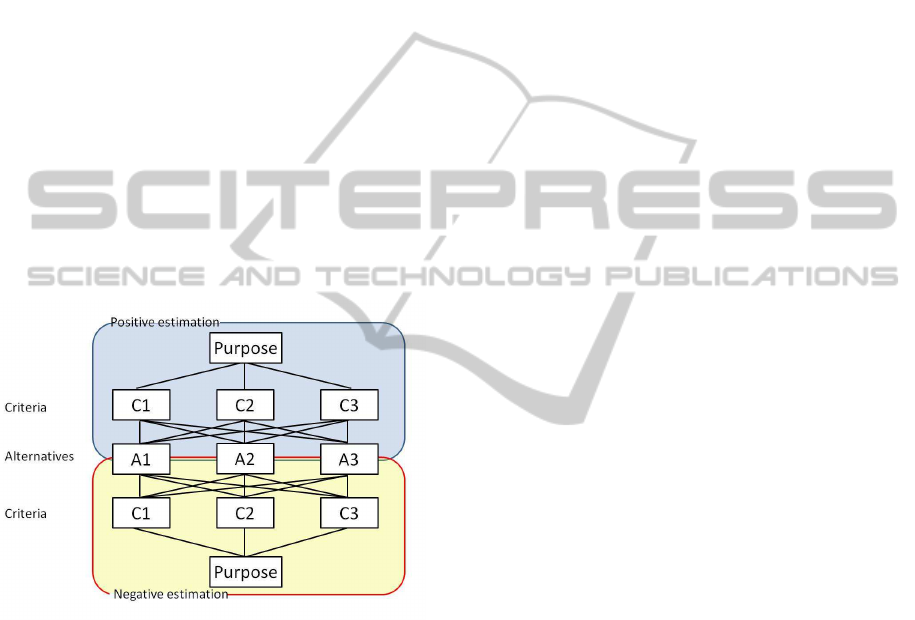
with dual construction in Fig. 1.
Figure 1: Dual hierarchy process.
Flowchart for proposed model is described as fol-
lows:
Step 1) decision-maker is asked to evaluate the de-
cision criteria and alternatives and to make up a pair-
wise comparison matrix in positive or negative.
Step 2) the consistency index between positive
matrix and negative matrix is calculated.
Step 3) If the judgments are consistent, final eval-
uation is obtained.
3.1 Positive Pairwise Comparison
Matrix
We define two matrices in order to propose new de-
cision model which has dual construction. One is the
superiority pairwise comparison matrix (positive ma-
trix) and another one is the inferiority pairwise com-
parison matrix (negative matrix).
The positive matrix is described by the ratio scale
of criterion, the same as AHP. The ordered set of
sequenced item by positive evaluation is defined as
X = x
1
,...,x
n
, in an certain decision problem. If the
magnitude relation of x
i
and x
j
is x
i
≥ x
j
and its ra-
tio is ω
i
: ω
j
, then positive matrix P having ω
i
/ω
j
is
constructed:
P =
ω
1
/ω
1
... ω
1
/ω
j
... ω
1
/ω
n
ω
2
/ω
1
... ω
2
/ω
j
... ω
2
/ω
n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
ω
n
/ω
1
... ω
n
/ω
j
... ω
n
/ω
n
(1)
The relation between matrix P and its eigenvector
is given as
Pω = nω (2)
where
ω
T
= [ω
1
,ω
2
,...,ω
n
].
3.2 Negative Pairwise Comparison
Matrix
We consider the opposite problem which has the order
relation x
j
≥ x
i
. When the ratio scale of each item is
defined as ω
j
: ω
i
, the negative matrix N constructed
by x
j
≥ x
i
is defined as
N =
ω
1
/ω
1
... ω
j
/ω
2
... ω
n
/ω
1
ω
1
/ω
2
... ω
j
/ω
2
... ω
n
/ω
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
ω
1
/ω
n
... ω
j
/ω
n
... ω
n
/ω
n
. (3)
where N = P
T
and P and N is the duality relation for
≥. Then, the relation between N and its eigenvector
is given as
Nω
′
= nω
′
(4)
where
ω
′T
= [1/ω
1
,1/ω
2
,...,1/ω
n
].
By the above definition, Eq. (4) could be derivedfrom
Eq. (2) and we acquire that both matrices is the dual-
ity relation by duality theorem: They are in the rela-
tion that the order is reversed.
In Step 1, positive matrix and negative matrix are
obtained by each evaluation of decision-maker. Se-
lect n − 1 combinations (nFnumber of elements) of
element he want in order to reduce the burden on
decision-maker’s task to compare. Then, it is not nec-
essary to check each consistency of matrix because 2
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
686

combinations is minimum number of combinations to
be able to calculate all evaluations.
All order, whether in human thinking, involves
proportionality among the parts. Thus, to create pos-
itive matrix or negative matrix, we must use ratio
scales to capture and synthesize the relations inherent
in that order. If, for example, to create positivematrix,
decision-maker is comparing each element according
to wight we ask: ”How much important is the ele-
ment i than the element j in proportion ?” or ”How
much inferior is the element i than the element j in
proportion ?” If the answer, ” i is more important than
j in proportion of 8 parts to 2” is gotten, the score of
pairwise comparison is ω
i
/ω
j
= 8/2. In positive and
negative evaluations, it is better to compare pair of el-
ements as differently as possible. Thus, the contradic-
tion between positive question and negative question
can be made easy to discover.
3.3 Consistency
In step 2, we must judge the consistency for the con-
structed matrix. There are two kinds of consistency.
One is the consistency of each matrix. Another is the
consistency of duality matrices. In this paper, Saaty’s
method (T.L.Saaty, 1980) is adopted for the former
and new method is proposed for the latter.
3.3.1 Consistency for Each Matrix
Next, consistency of each matrix is checked. The pro-
posed positive matrix and negative matrix are consis-
tent because their values are consisted by n−1 of ratio
and other values are calculated at the them.
However, if values are obtained by comparing
the pair of elements as AHP, we adopt the Saaty’s
method. Saaty proved that for consistent reciprocal
matrix, the largest eigen value is equal to the size of
comparison matrix, or λ
max
= n. Then a measure of
consistency, called Consistency Index is given as de-
viation or degree of consistency using the following
formula
CI =
λmax− n
n− 1
. (5)
3.3.2 Consistency in Duality
We propose how to judge the consistency in duality
between P and N. The consistency in duality means
that positive and negative have same order of priority
in criteria and alternatives. It is necessary to examine
the consistency of duality to discover implicit contra-
diction of the decision-maker.
We apply the concept of reachability matrix to
our procedure. If proposed consistency is satisfied
completely, the order relation between P and N is
duality. We defined, the relation of priorities in
positive and negative matrices is not reversed and it
should be considered within the acceptable limits.
Step1) creation of adjacency matrix
Both matrix P and N can be represented by a ma-
trix M, called the adjacency matrix, as shown below.
There is a row and column for each node; M[i, j] = 1
if (i, j) element of matrix is more than 1, if (i, j) ele-
ment is otherwise M[i, j] = 0.
M
P
= [m
P
ij
]
M
N
= [m
N
ij
] (6)
m
ij
=
1 :ω
ij
≥ 1
0 :ω
ij
< 1orunknown
where M
P
is the adjacency matrix of P and M
N
is the
adjacency matrix of N.
Step2) creation of reachability matrix
The next step derives the reachability matrices R
P
and R
N
. It is calculated on gotten the adjacency ma-
trices with Boolean OR operation as follows:
R
P
=
m
∑
k=1
M
k
P
(7)
R
N
=
m
∑
k=1
M
k
N
(8)
When the number of k(≤ m) is added up, the ele-
ments of adjacency matrix M converge in specific k.
Then, the convergent matrix is reachability matrix. If
R(i, j) = 1 then it means i element is more important
than j element. if R(i, j) = 0 then i is less important
than j, respectively. Thus, R represents the relation
of important degree in n-tuple pairwise comparison.
Step3) judgement of the consistency of duality
In the last step, we judge the consistency of dual-
ity on P and N. When obtaining R
P
and R
N
in step2
have same elements, it is defined by ω = 1/ω
′
that
both matrices are consistent in duality. To judge the
consistency, matrix C is defined as
R
P
⊕ R
T
N
= C (9)
where operator ⊕ represents exclusive OR. As C =
O(where O is zero matrix)Cwe define the relation be-
tween P and N as being consistent. On the other hand,
as C 6= O, it suggests that there is an inconsistency of
order about i and j where 1 in C.
DECISION MAKING BASED ON DUALITY BETWEEN POSITIVE AND NEGATIVE EVALUATIONS
687

4 APPLICATION
The following example is taken from the paper pre-
sented by H.S.Rian and T.Sekiguchi (RIAN and
Takashi, 1995). Suppose that a company choices a
excellent person in three persons A
1
, A
2
and A
3
, on
decision-making for person perception. Decision cri-
teria are as follows:
• sense of responsibility (C
1
)
• inventive idea (C
2
)
• knowledge (C
3
)
Decision-maker gives two values (n = 3) through
a pairwise comparison of above criteria in positive
and negative. In positive criteria, for example, to ask
a decision-maker ”Which is more important a sense
of responsibility or an inventive idea for person per-
ception ?”. In negative, ”Which doesn’t need a sense
of responsibility or an inventive idea for person per-
ception ?”. Then, he gives the ratio as pairwise com-
parison value. Table 1 and Table 2 are results given
by a decision-maker through a pairwise comparison.
Values in square are calculated by given comparison
value. Both tables consisted of n − 1 values are satis-
fied in Saaty’s C.I..
Table 1: Positive pairwise comparison by personality.
C
1
C
2
C
3
C
1
1 8/2 24/4
C
2
1 6/4
C
3
1
Table 2: Negative pairwise comparison by personality.
C
1
C
2
C
3
C
1
1 3/7 2/8
C
2
1 7/12
C
3
1
In next step, we check the dual consistency. Two
adjacency matrixes are created from Table 1 and Table
2 by Eq. (7).
M
P
=
1 1 1
0 1 1
0 0 1
,M
N
=
1 0 0
1 1 0
1 1 1
.
Then, reachability matrixes R
P
and R
N
are ob-
tained as
R
P
=
1 1 1
0 1 1
0 0 1
,R
N
=
1 0 0
1 1 0
1 1 1
.
Finally, the dual consistency index C can be calcu-
lated by Eq. (9).
C = O
In the calculation, C is zero matrix. It shows that
the dual consistency is satisfied under criteria. More-
over, both eigen vectors of maximum eigen values are
weight vector on criteria, givens as
W
T
P
= (0.706,0.176,0.118)
W
T
N
= (0.136,0.318,0.546).
By the above result, the order relation isC
1
≥ C
2
≥ C
3
in positive and negative. It shows that they are duality
in order relation.
5 CONCLUSIONS
This paper suggested a new decision-making model
to analyze the human’s double psychology in fraud
prevention.
We proposed the dual hierarchy, having posi-
tive matrix and negative matrix to evaluate two-sided
question. We discussed about the relation that both
matrixes are duality. Further, the technique to judge
a dual consistency of both matrixes, provides consis-
tency index based on a concept of reachability matrix
through the order relation of both matrixes. As a re-
sult, we are able to check any inconsistency between
positive and negative mentals.
In our future work, we plan to develop a method
for fraud detection with our decision-making model.
REFERENCES
Ataka, H. (1966). Boolean algebra. Kyouritsu, Japan.
Azuma, R. and Miyagi, H. (2009). Ahp for risk manage-
ment based on expected utility theory. In IEEJ C,
EISS. IEEJ.
RIAN, H. S. and Takashi, S. (1995). Decision-making of
person perception by the observed quantities : Prob-
lem of the person perception and personnel choice by
the extended fuzzy relation equation. Japan Society
for Fuzzy Theory.
T. L. Saaty (1980). The Analytic Hierarchy Process. Mc-
GrawHill.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
688
