
A SPATIAL QUERY LANGUAGE
FOR PRESENTATION-ORIENTED DOCUMENTS
Ermelinda Oro
DEIS, University of Calabria, Via P. Bucci 41/C, 87036 Rende (CS), Italy
Francesco Riccetti, Massimo Ruffolo
ICAR-CNR, University of Calabria, Via P. Bucci 41/C, 87036 Rende (CS), Italy
Keywords:
Information extraction, Web wrapping, PDF wrapping, Spatial reasoning, Grammars, Chart parsing.
Abstract:
In last years the huge relevance of accessing and acquiring information made available by Web (HTML) pages
and business (PDF) documents has grown much further. In this paper we present a textual query language,
named ViQueL, whose main feature is to identify and extract relevant information from HTML and PDF docu-
ments on the base of their visual appearance by using easy-to-write queries. The proposed language is founded
on spatial grammars, i.e. context free grammars extended by spatial constructs. Despite a considerable ex-
pressive power, combined complexity of ViQueL is in P-Time. Moreover, experiments show that ViQueL is
reasonably efficient for real-life extraction tasks.
1 INTRODUCTION
In the literature is available a large body of work
on formalisms and approaches aimed at manipulat-
ing contents of HTML and PDF documents. Exist-
ing approaches broadly fall in the following main ar-
eas: (i) visual languages aimed at manipulating visual
information for extraction and transformation scopes
(Kong et al., 2006); (ii) web information extraction
approaches that allow for extracting relevant infor-
mation by exploiting mainly the visual appearance of
Web pages (Baumgartner et al., 2001), or their inter-
nal representation (Cafarella et al., 2008); (iii) PDF
wrapping approaches that enable to acquire informa-
tion from PDF documents (Hassan and Baumgartner,
2005); (iv) approaches aimed at manipulating con-
tents of presentation-oriented documents (Adali et al.,
2000; Lee et al., 1999). Nevertheless existing ap-
proaches suffer from the following main drawbacks:
(i) they do not allow for querying the visual structure
of both HTML and PDF documents in a user friendly
way; (ii) they are frequently task oriented so each of
them deal with a specific problem like record extrac-
tion, table extraction and so on; (iii) frequently their
computational costs are unknown.
In this paper we present a query language, named
ViQueL and based on our previous work (Oro et al.,
2009), that allows for querying both Web and PDF
documents in order to recognize a wide variety of
content structures (e.g. repetitive records, tables,
news, infoboxes, profiles, etc) by exploiting their spa-
tial arrangement. The proposed language is founded
on spatial grammars (SGs), i.e. context free grammars
extended by spatial constructs coming from the rect-
angular cardinal relation formalism (Navarrete and
Sciavicco, 2006). ViQueL exploits a spatial docu-
ment model (SDM) in which each document is viewed
as a two-dimensional Cartesian plan on which are
placed rectangles called content items (CIs). A query
on a document is constituted by a set of spatial pro-
duction rules (SPR) of the SG. Basically SPRs de-
scribe how to spatially compose CIs on the plane in
order to identify meaningful content structures. Doc-
ument querying is obtained by parsing the SDM using
SPRs in the query. The parsing strategy is an ad hoc
extension of the CYK parsing algorithm. It is note-
worthy that ViQueL queries can be used for recogniz-
ing a given content structure in different documents
having also different internal encodings. In fact, the
SDM constitutes an abstraction of underlying inter-
nal representation. Experiments on real cases show
how the ViQueL language is pretty much simple and
how it allows users for querying presentation oriented
documents on the base of what they see. Experiments
306
Oro E., Riccetti F. and Ruffolo M..
A SPATIAL QUERY LANGUAGE FOR PRESENTATION-ORIENTED DOCUMENTS.
DOI: 10.5220/0003177603060312
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 306-312
ISBN: 978-989-8425-40-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

show also that the adopted parsing strategy make the
extraction process reasonably efficient.
The paper is organized as follows. Section 2
presents the spatial document model. In Section
3 syntaxt and semantics of ViQueL is presented
by using some running examples. Section 4 for-
mally presents syntax and semantics of the ViQueL
language, describes the spatial CYK algorithm and
shows languages complexity issues. Section 5 is
about results of experiments. Finally Section 6 con-
cludes the paper and sketches future work.
2 THE SPATIAL DOCUMENT
MODEL
In this paper we subsume documents encoded by
HTML or PDF formats as presentation-oriented doc-
uments (PODs). In the rest of the paper we will as-
sume PODs as represented by the spatial document
model (SDM). Broadly speaking the main idea which
this model is based on is that the area of the screen
aimed at visualizing a POD can be viewed as a 2-
dimensional Cartesian plane on which is arranged a
set of content items (CIs). A CI is an atomic piece
of content (i.e. an images, an alphanumeric string
written with unique font features, a graphical or typo-
graphical element like: a line, a circle etc.) visualized
in a rectangular area of the plane. So the spatial doc-
ument model of a POD consists in a set of CIs which
are formally defined as follows.
Definition 1. Let T be a set of type names arranged
in a taxonomy, a content item is a 6-tuple of the form:
CI = hτ,σ, r
−
x
, r
−
y
, r
+
x
, r
+
y
i
where:
• τ ∈ T is the type of the content item (e.g. image,
text, number, percentage, currency, etc).
• σ is the value of the content item (e.g. a string, the
URL of an image, etc).
• The pairs (r
−
x
, r
−
y
) and (r
+
x
, r
+
y
) represent two
points on the Cartesian plane that identify the
bottom-left, and top-right vertices respectively, of
the rectangle that surround the contents σ (see
Figure 1).
Figures 1 and 3 show some CIs computed as de-
scribed in Section 5.
3 QUERYING PODS BY VIQUEL
The scope of this section is to give a by example and
intuitive explanation of ViQueL capabilities and fea-
tures. The language is more rigorously presented and
discussed in following Sections.
Example 1. The example in Figure 1 shows a charac-
teristic Deep Web page in which are contained a set
of repetitive records. In Figure 2 is highlighted one
of the record in Figure 1. The spatial arrangement
of CIs, and the type of their contents, help human
readers to immediately understand the meaning of the
record. For identifying and extracting all records in
that page, the user can pose the following ViQueL
query.
1. S
W
→ img A
2. A
E
→ B C
3. B
W
→ text B
4. B
W
→ text text
5. C
N
→ text text
The query is constituted by spatial production
rules of the spatial grammar (see Section 4.2). The
SPR 5 express that a new composed CI (identified by
the non-terminal symbol C) can be derived when two
CIs of type text are in the spatial relation north (
N
→).
In Figure 2 such a production compose the name of
the product (first terminal text) and its description
(second terminal text). The name of the product, in
fact, is on top (north) of the description. SPRs 3 and
4 allow for recursively identifying sequence of CIs.
So the non terminal B identifies a sequence of CIs in
which each CI is at west (
W
→) of the others (the be-
havior of the rules is shown in Figure 2 by using the
non-terminal symbol B two times). The SPR 2 allows
for obtaining a new composed CI (represented by the
nonterminal A) by combining non terminals B and C
along the east (
E
→) direction. Finally, the SPR 1 com-
pletes the records (axiom S) including the picture (ter-
minal img) which is located at west (
W
→) of A.
Figure 1: The Ebay Web Page with some Highlighted CIs.
Example 2. Figure 3 depicts information in tabular
form contained in a PDF document. The query for
this example is shown in the following.
1. S
N
→ HEADER BODY
A SPATIAL QUERY LANGUAGE FOR PRESENTATION-ORIENTED DOCUMENTS
307

Figure 2: A Record with Associated CIs.
2. HEADER
E
→ HEADER text
3. HEADER
E
→ text text
4. BODY
S
→ ROW BODY
5. BODY
S
→ ROW ROW
6. BODY → ROW
7. ROW
W
→ text DATA
8. DATA
E
→ percent NUMBERS
9. NUMBERS
W
→ NUMBERS number
10. NUMBERS
W
→ number number
The following set of CI types are used: text that
represents plain text, number that represents inte-
ger and floating point numbers and is is
a of text,
percent that represents percentage and is a sub type
of number.
Figure 3: Table in a PDF Document with Highlighted CIs.
SPRs 9 and 10 (that use nonterminal symbol
NUMBERS) constitute a recursion that allow for cap-
turing composed CIs constituted by sequence of num-
bers (terminal symbol number) along the west direc-
tion (
W
→). SPR 8 allows for creating composed CIs
(identified by nonterminal DATA) constituted by the
composition, along the east direction (
E
→), of a per-
centage (terminal symbol percent) and a composed
CI identified as a NUMBERS. A row of the table (non-
terminal ROW) is obtained by composing, along the
west direction, a text CI and a composed CI DATA.
SPRs 4, 5 and 6 use non-terminal BODY to identify the
body of the table as a sequence of rows. A BOBY is
a composed CI that can correspond to a single ROW
(SPR 6 that acts as an isa relation) or to a recursive
sequence of ROWs in the south direction (
S
→). SPRs
2 and 3, based on nonterminal HEADER, identify the
header of the table as a sequence of text-type CIs.
Finally, rule 1 combines header and body in order to
identify the whole table in the axiom S. It is notewor-
thy that tables can be identified and extracted from
Web documents in the same way. For lack of space we
don’t show here a related example.
4 VIQUEL
In this section we give the formal definition of
ViQueL. We first introduce the preliminary concept
of Rect used for defining the language, then present
language syntax, semantics and complexity issues.
4.1 Rectangular Cardinal Relations
In the Rectangular Cardinal Relations model (RCR)
proposed in (Navarrete and Sciavicco, 2006), let
r
1
and r
2
be two rectangles, spatial relations are
expressed by analyzing the 9 regions (cardinal
tiles) formed by the projections of the sides of a
reference rectangle along the axes of the Carte-
sian plane. By considering cardinal tiles, atomic
RCRs are traditionally expressed by means of the
9 symbols contained in the following set R
A
card
=
{B, S, SW, W, NW, N, NE, E, SE}. The sym-
bol B denotes the central tile and the relation be-
longs to. Other symbols in R
A
card
correspond to the
peripheral tiles and denote the eight RCRs South,
SouthWest, West, NorthWest, North, NorthEast,
East, and SouthEast. Given ρ ∈ R
A
card
, the expres-
sion r
1
ρ r
2
means that r
2
lies entirely on the tile ρ of
r
1
. When a rectangle r
2
overlaps with several tiles rel-
ative to a reference rectangle r
1
, we call the relation
that links r
2
to r
1
multi-tile relation and represent it by
ρ
1
: ··· : ρ
k
where ρ
1
, ..., ρ
k
are atomic RCRs. Atomic
and multi-tile relations are called Basic RCR. For in-
stance, by considering the RCR r
1
E:NE r
2
between
a reference rectangle r
1
and another rectangle r
2
, the
RCR relation E:NE means that the rectangle r
2
lies on
the tiles that are on east and north-east of the rectangle
r
1
. In the RCR model, the set R
card
of all basic RCRs
between any couple of MBRs contains 36 elements
(Navarrete and Sciavicco, 2006).
4.2 Language Syntax and Semantics
In the following we introduce the concept of spa-
tial grammar, give language semantics in terms of
the parsing technique adopted for computing ViQueL
queries, and present complexity results.
Definition 2. A spatial grammar is a 5-tuple of the
form:
SG = (Σ, N, S, R
rec
, Π)
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
308

where: (i) Σ is a set of terminal symbols that corre-
sponds to CI types and identifies all the CIs in a SDM.
(ii) N is a set of nonterminal symbols that identifies
composed content items which structure is in Defini-
tion 3 below. (iii) S ∈ N is the grammar axiom. (iv)
R
rec
is the set of basic cardinal direction relation in-
troduced in Section 4.1. (iv) Π is a finite set of spa-
tial production rules (SPRs) of the form A
dir
→ αβ and
A→α, where: A ∈ N, α, β ∈ (Σ ∪ N), and dir ∈ R
rec
.
Sets Σ, N and R
rec
, are disjoint and finite.
In order to explain how spatial grammars works
we have to define the concept of composed content
item (CCI) as follows.
Definition 3. A composed content item (CCI) is a 6-
tuple of the form:
CCI = hΓ,A, r
−
x
, r
−
y
, r
+
x
, r
+
y
i
where:
• Γ is a non empty set of spatially contiguous CIs.
• A is the identifier of the CCI corresponding to a
nonterminal symbol of the SG.
• r
−
x
= min (r
−
x
γ
|γ ∈ Γ ∧ γ = (τ, σ, r
−
x
γ
, r
−
y
γ
, r
+
x
γ
, r
+
y
γ
))
• r
−
y
= min (r
−
y
γ
|γ ∈ Γ ∧ γ = (τ, σ, r
−
x
γ
, r
−
y
γ
, r
+
x
γ
, r
+
y
γ
))
• r
+
x
= max (r
+
x
γ
|γ ∈ Γ ∧ γ = (τ, σ, r
−
x
γ
, r
−
y
γ
, r
+
x
γ
, r
+
y
γ
))
• r
+
y
= max (r
+
y
γ
|γ ∈ Γ ∧ γ = (τ, σ, r
−
x
γ
, r
−
y
γ
, r
+
x
γ
, r
+
y
γ
))
CIs in Γ are spatially contiguous when the area de-
fined by r
−
x
γ
, r
−
y
γ
, r
+
x
γ
, r
+
y
γ
do not overlaps with other CIs
not in Γ.
A SPR of the form A→α, where α ∈ Σ, and A ∈ N
allows for creating a CCI corresponding to a CI iden-
tified by the terminal symbol α. This operation con-
stitutes a generalization of the terminal α into the non-
terminal A, and at the same time a transformation of
the CI related to α into the CCI related to A. Rules of
the form A
dir
→ α β, where α, β ∈ Σ, and A ∈ N, com-
pose the two contiguous CIs related to the terminal
symbols α and β, along the direction specified by the
relation
dir
→, in order to obtain a new CCI A having the
structure described in Definition 3. SPRs having the
form A
dir
→ BC, where A, B,C ∈ N, compose the sets Γ
B
and Γ
C
of CIs in the CCIs related to the nonterminals
B and C respectively, in order to obtain a new CCI
having coordinates computed as specified in Defini-
tion 3. Similar considerations can be done for rules
that combine terminal and nonterminal symbols.
4.2.1 The Spatial CYK Algorithm
In the following we present the pseudo-code of the
SCYK algorithm. Computational complexity aspects
are discussed in Section 4.2.2. Before presenting the
algorithm we define a CNF-like normal form that al-
lows a shortest and more intuitive pseudo-code. It is
obviously possible and easy to extend the algorithm
to parse any type of rules.
Definition 4. A SG is in SG-normal form if all its
production rules are either in the form A
dir
→ BC, or
A → α where A,B and C are non-terminals, while α
is a terminal symbol. Production of type A → α are
called unary spatial production rules.
The algorithm takes as input a SG Q and a set of CIs
D. In instruction 1 the algorithm creates two ordered
sets L
x
and L
y
that contain coordinates r
−
x
and r
−
y
of
all CIs ∈ D respectively.
In the worst case n = |L
x
| and m = |L
y
| can be at
most equal to the size of the document |D|, but in real
cases both have a size smaller than |D|. In instruction
4 SPRs in Q are acquired in the set RS. Instruction 6
assigns to RS
U
all unary SPRs in RS. In instruction
7 non unary SPRs are split in two subsets RS
H
and
RS
V
that contain rules of the type V
dir
→ XY , where dir
is a RCR that expresses relations obtained from the
subsets of basic RCR {E, SE, NE, W, SW, NW , B} for
RS
H
and {N, NW, NE, S, SE, SW , B} for RS
V
.
Instructions 8 and 9 generate tables T
1
and T
2
re-
spectively. Indices in the first four positions of T
1
and
T
2
, namely i
2
, i
1
, j
2
, and j
1
identify the CCI having as
bottom-left vertex (L
x
[i
2
], L
y
[ j
2
]) and as top-rigth ver-
tex (L
x
[i
2
+ i
1
], L
y
[ j
2
+ j
1
]). The last position in table
T
1
contains a nonterminal symbol.
The general idea which guides the algorithm is
that elements in T
2
represent CCIs by the correspond-
ing coordinates, while elements in T
1
are boolean val-
ues that state if a given nonterminal symbol V in the
grammar is associated to the corresponding CCI in T
2
(it is noteworthy that a CCI can have different asso-
ciated nonterminal symbols). Instruction 10 creates a
two-dimensional table I where elements I[i
1
, j
1
] con-
tain a set of couples < i
2
, j
2
> which indicate that
the CCI in T
2
[i
2
, i
1
, j
2
, j
1
] is not null. Instruction 11
creates the table res that represents the result of the
algorithm (i.e. the set of CCIs that satisfies the ax-
iom S in the grammar Q). Instruction 12 initializes
tables T
1
, T
2
, and I by using the set D of input CIs
and the set RS
U
of unary SPRs. The initialization
procedure works as follows: if an area having as ver-
tices (L
x
[i
2
], L
y
[ j
2
]) and (L
x
[i
2
+ i
1
], L
y
[ j
2
+ j
1
]) con-
tains only one CI, the couple < i
2
, j
2
> is added to
I[i
1
, j
1
] and T
2
[i
2
, i
1
, j
2
, j
1
] is filled by entering coor-
dinates of that CI. Let α be a CI type (i.e. a terminal
symbol), then for each unary rule V → β, where β
isa α (isa is computed by using the taxonomy of CI
types), element T
1
[i
2
, i
1
, j
2
, j
1
,V ] is set to true (such
an operation corresponds to the generation of a CCI
for each initial CI). Remaining values in tables T
1
, T
2
and I are computed in the main loop (instructions 13-
A SPATIAL QUERY LANGUAGE FOR PRESENTATION-ORIENTED DOCUMENTS
309

Algorithm 1: Spatial CYK.
Input : A SG Q and a set D of CIs (i.e. the document)
Output: A set of CCIs that satisfy the grammar Q
1 < L
x
, L
y
> = createOrderedCoordinateSets(Q);
2 n = |L
x
|;
3 m = |L
y
|;
4 RS =getRuleSet(Q);
5 R = getNonTerminalNumber(RS);
6 RS
U
= getRuleSet(RS);
7 < RS
H
, RS
V
> = splitRuleSetByDirection(RS − RS
U
);
8 createTable T
1
[n, n, m, m, R];
9 createTable T
2
[n, n, m, m];
10 createTable I[n, m];
11 createSet res;
12 < T
1
, T
2
, I >=initialize(D, RS
U
);
13 for i
1
← 1 to n do
14 for j
1
← 1 to m do
15 for j
3
← 1 to j
1
− 1 do
16 indexSet = I[i
1
, j
3
];
17 foreach < i
2
, j
2
> ∈ indexSet do
18 if j
2
+ j
1
≤ m then
19 for i
3
← i
1
downto 1 do
20 ver(i
2
, i
1
, j
2
, j
1
,i
1
, j
3
,
i
2
, i
3
, j
2
+ j
3
, j
1
− j
3
,
T
1
, T
2
, RS
V
, res);
21 end
22 end
23 end
24 end
25 for i
3
← 1 to j
1
− 1 do
26 indexSet = I[i
3
, j
1
];
27 foreach < i
2
, j
2
> ∈ indexSet do
28 if i
2
+ i
1
≤ n then
29 for j
3
← j
1
downto 1 do
30 ver(i
2
, i
1
, j
2
, j
1
,i
3
, j
1
,
i
2
+ i
3
, i
1
− i
3
, j
2
, j
3
,
T
1
, T
2
, RS
H
, res);
31 end
32 end
33 end
34 end
35 end
36 end
37 return < res, T
1
>;
36). CCIs of increasing sizes are discovered by iterat-
ing with the two most external cycle by using indexes
i
1
(to increase length) and j
1
(to increase height) in
instructions 13 and 14 respectively. Two different in-
ternal loops are then used in order to find larger CCIs
in horizontal and vertical directions respectively, by
merging contiguous CCIs. In instruction 15 each iter-
ation uses pairs < i
2
, j
2
> in the entry I[i
1
, j
3
] of table
I (instruction 16) in order to consider each existing
CCI cci
1
having width equals to |L
x
[i
2
+ i
1
] − L
x
[i
2
]|
and height equals to |L
y
[ j
2
+ j
3
] − L
y
[ j
3
]|. The inner
Procedure ver(i
2
,i
1
, j
2
, j
1
,i
1
0
, j
1
0
,i
2
00
, i
1
00
, j
2
00
, j
1
00
,T
1
,
T
2
, RS, res).
1 p
1
= Q[i
2
, i
1
0
, j
2
, j
1
0
];
2 p
2
= Q[i
2
00
, i
1
00
, j
2
00
, j
1
00
];
3 if p
2
6= null then
4 foreach V
dir
→ XY ∈ RS
V
do
5 c
1
= T
1
[i
2
, i
1
0
, j
2
, j
1
0
, X ] ∧ T
1
[i
2
00
, i
1
00
, j
2
00
, j
1
00
,Y ] ∧
(p
1
dir p
2
);
6 c
2
= T
1
[i
2
, i
1
0
, j
2
, j
1
0
,Y ] ∧ T
1
[i
2
00
, i
1
00
, j
2
00
, j
1
00
, X ] ∧
(p
2
dir p
1
);
7 if c
1
∨ c
2
then
8 T
1
[i
2
, i
1
, j
2
, j
1
,V ] ← true;
9 update(T
2
[i
2
, i
1
, j
2
, j
1
]);
10 if V is axiom then add(res,T
2
[i
2
, i
1
, j
2
, j
1
]);
11 end
12 end
13 break;
14 end
cycle (Instruction 19 and procedure veri f y in instruc-
tion 20) takes (if exists) the widest CCI cci
2
contigu-
ous to cci
1
. It is necessary to iterate from i
1
to 1 with
index i
3
because we have to consider also inclusion
relations (B) between two CCIs. If we don’t con-
sider inclusion relation we can take as contiguous CCI
cci
2
the one having as corners (L
x
[i
2
], L
y
[ j
2
+ j3])
and (L
x
[i
2
+ i
3
], L
y
[( j
2
+ j3), ( j
1
− j3)]). If such CCI
exists the algorithm examines each rule V
dir
→ XY ∈
RS
V
. If values of the two elements in T
1
referring to
(cci
1
, X ) and (cci
2
,Y ) are true and cci
1
is at dir to
cci
2
then T
1
[i
2
, i
1
, j
2
, j
1
,V ] is set to true and value of
T
2
[i
2
, i
1
, j
2
, j
1
] is set to the proper dimension of the
CCI. If V is the start symbol in Q, the CCI just found
is added to the result set res. Specular operations are
done in the second sub-loop in order to evaluate SPRs
in RS
H
. At the end the algorithm returns the set res
containing founded CCIs and the table T
1
that can be
used for generating the query (grammar) parse tree by
a trace-back procedure.
4.2.2 Complexity Issues
Theorem 1. Let D be the SDM of a presentation-
oriented document, the evaluation of a ViQueL
query Q, performed by Algorithm 1, requires space
O(|D|
4
· |Q|) and time O(|D|
6
· |Q|), where |D| and |Q|
are the size of the document in terms of CIs and the
size of the query in terms of SPRs respectively.
Proof. Space complexity. Memory usage of the
algorithm corresponds to the size of table T
1
. In ta-
ble T
1
, R represents the number of nonterminals in
the query Q, so the space complexity is O(m
2
· n
2
· R).
Since the number of non terminals can be at most |Q|,
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
310
and in the worst case we have that m = n = |D|. The
space complexity bound O(|D|
4
· |Q|) follows. ♦
Proof. Time complexity. Filling ordered sets L
x
and L
y
can be done in O(|D| · lg(|D|)). Comparisons
in the algorithm can be all done in constant time
using appropriate data structures. Remember also
that m and n are both bounded by |D|. Operations
concerning splitting of SPRs in Q are done in linear
time, i.e. O(|Q|). Initialization procedure can be
performed in O(|D|
2
· |Q|). Main loop is clearly the
part of the algorithm that takes more time. Procedure
veri f y is manifestly in O(|Q|). The maximum
number of couple < i
2
, j
2
> that can be contained in
a element I[i
1
, j
1
] of table I is O(m · n), in the worst
case scenario we have O(|D|
2
)) because m = n = |D|.
So time complexity in the worst case is computed
as O(n · m · (m
2
· n · (n · |Q|) + n
2
· m · (m · |Q|))) =
O(n
3
· m
3
· |Q|) , i.e. O(|D|
6
· |Q|). ♦
5 EXPERIMENTS
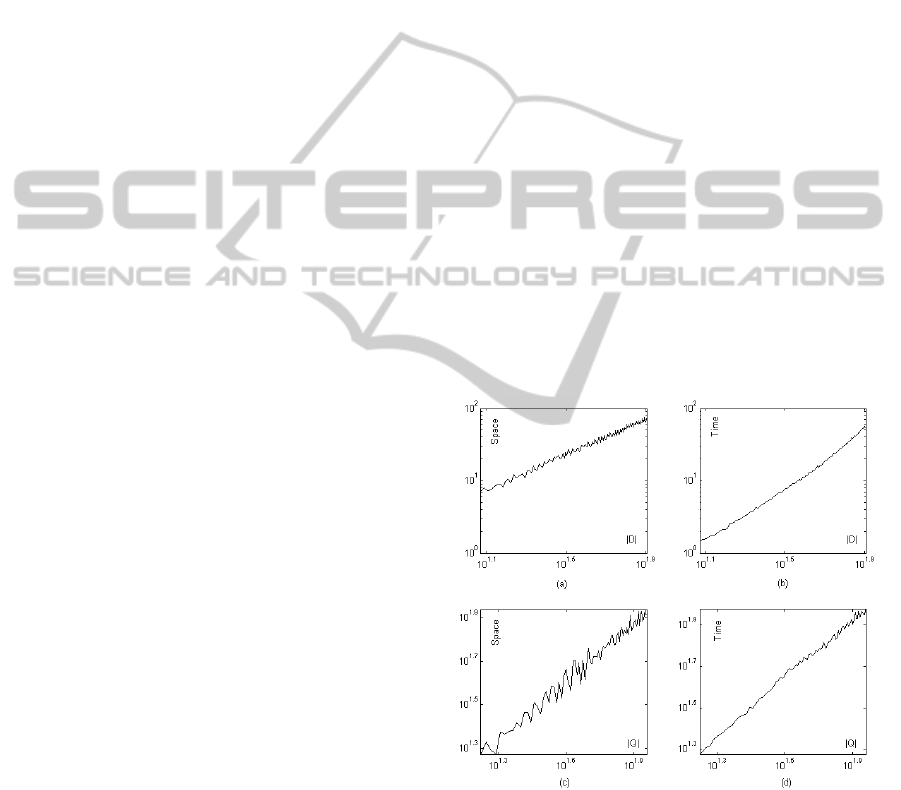
In Figure 4 are shown results of experiments carried
out for empirically verify Theorem 1. We ran experi-
ments on a Windows 7 machine with 2,53 GHz Intel
core-duo processor and 4 GB of RAM. We considered
the table and the query in Example 2 and linearly in-
creased their sizes by adding table rows and dummy
rules respectively. Figures 4a and 4b show required
space and time for document sizes that grown from
|D| = 25 to |D| = 1020. Figures 4c and 4d show re-
quired space and time considering query sizes form
|Q| = 10 to |Q| = 108. Curves in the figures refer to
normalized values and has been drown in loglog scale.
Experiments show that required space in the average
case is linear w.r.t. both the size of Q and D, while
required time, in the average case, is linear w.r.t. the
size of Q and polynomial (with a degree smaller that
in the worst case) w.r.t. the size of D. In Example 2
the system takes about 200 milliseconds for recogniz-
ing the table, so the implemented system results effec-
tively usable in real cases. We have, also, performed
usability experiments by asking 10 user to learn the
language and apply it for extracting tables and data
records from a dataset composed of 5 PDF documents
and 5 web pages. Experiments have shown that the
language is easy to learn and that can by intuitively
applied for real extraction tasks. We don’t give further
details about usability experiments for lack of space.
6 CONCLUSIONS AND FUTURE
WORK
In this paper we presented ViQueL, a spatial
query language that allow for querying presentation-
oriented documents on the base of their visual ap-
pearance. The language is founded on spatial gram-
mars that are obtained by combining classical con-
text free grammars and qualitative spatial reasoning
constructs. The main feature of ViQueL is that it al-
lows for easily defining visual queries that enable to
recognize complex content structures in both HTML
and PDF documents. ViQueL queries are computed
by the SCYK algorithm, a spatial extension of the
well known CYK algorithm. Despite the increased
expressiveness of spatial grammars, the complexity
of the SCYK algorithm remains in P-Time. Further-
more, experiments prove that the algorithm is effi-
cient and usable in real-life cases with satisfactory
results. The proposed approach can be improved by
adopting a stochastic extension to SGs in order to
better manage ambiguous queries. As future work
we intend to apply inductive approaches for learning
ViQueL from portions of documents visually selected
by users. This way no manual code writing will be
required to the users.
Figure 4: Results of Experiments.
REFERENCES
Adali, S., Sapino, M. L., and Subrahmanian, V. S. (2000).
An algebra for creating and querying multimedia pre-
sentations. Multimedia Syst., 8(3):212–230.
Baumgartner, R., Flesca, S., and Gottlob, G. (2001). Vi-
sual web information extraction with lixto. In VLDB
A SPATIAL QUERY LANGUAGE FOR PRESENTATION-ORIENTED DOCUMENTS
311

’01: Proceedings of the 27th International Conference
on Very Large Data Bases, pages 119–128, San Fran-
cisco, CA, USA. Morgan Kaufmann Publishers Inc.
Cafarella, M. J., Halevy, A., Wang, D. Z., Wu, E., and
Zhang, Y. (2008). Webtables: exploring the power of
tables on the web. Proc. VLDB Endow., 1(1):538–549.
Hassan, T. and Baumgartner, R. (2005). Intelligent text
extraction from pdf documents. In CIMCA/IAWTIC,
pages 2–6.
Kong, J., Zhang, K., and Zeng, X. (2006). Spatial graph
grammars for graphical user interfaces. ACM Trans.
Comput.-Hum. Interact., 13(2):268–307.
Lee, T., Sheng, L., Bozkaya, T., Balkir, N. H.,
¨
Ozsoyoglu,
Z. M., and
¨
Ozsoyoglu, G. (1999). Querying multime-
dia presentations based on content. IEEE Trans. on
Knowl. and Data Eng., 11(3):361–385.
Navarrete, I. and Sciavicco, G. (2006). Spatial reasoning
with rectangular cardinal direction relations. In ECAI,
pages 1–9.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
312
