ANNEXATIONS AND MERGING IN WEIGHTED VOTING GAMES

The Extent of Susceptibility of Power Indices

Ramoni O. Lasisi and Vicki H. Allan

Department of Computer Science, Utah State University, Logan, UT 84322-4205, U.S.A.

Keywords:

Agents, Manipulations, Annexation, Merging, Power indices.

Abstract:

This paper discusses weighted voting games and two methods of manipulating those games, called annexation

and merging. These manipulations allow either an agent, called an annexer to take over the voting weights of

some other agents in the game, or the coming together of some agents to form a bloc of manipulators to have

more power over the outcomes of the games. We evaluate the extent of susceptibility to these manipulations

in weighted voting games of the following prominent power indices: Shapley-Shubik, Banzhaf, and Deegan-

Packel indices. We found that for unanimity weighted voting games of n agents and for the three indices: the

manipulability, (i.e., the extent of susceptibility to manipulation) via annexation of any one index does not

dominate that of other indices, and the upper bound on the extent to which an annexer may gain while annexing

other agents is at most n times the power of the agent in the original game. Experiments on non unanimity

weighted voting games suggest that the three indices are highly susceptible to manipulation via annexation

while they are less susceptible to manipulation via merging. In both annexation and merging, the Shapley-

Shubik index is the most susceptible to manipulation among the indices.

1 INTRODUCTION

Weighted voting games (WVGs) are mathematical ab-

stractions of voting systems. In a voting system, vot-

ers express their opinions through their votes by elect-

ing candidates to represent them or inﬂuence the pas-

sage of bills. Each member of the set of voters, V, has

an associated weight w :V → Q

. A voter’s weight is

the number of votes controlled by the voter, and this

is the maximum number of votes she is permitted to

cast. The homogeneous voting system is a special case

in which all voters have unit weight (Levchenkova

and Levchenkov, 2002). In our context, a subset of

agents, called the coalition, wins in a WVG, if the

sum of the weights of the individual agents in the

coalition meets or exceeds a certain threshold called

the quota. In the more traditional homogeneous vot-

ing system, the winning coalition is determined by the

majority of the agents. However, in WVGs with all

agents having different weights, a coalition with sum

of the individual agents’ weights meeting or exceed-

ing the quota determines the winning coalition.

It is natural to naively think that the numeri-

cal weight of an agent directly determines the cor-

responding strength of the agent in a WVG. The

measure of the strength of an agent is termed its

power. This is the ability of an agent to inﬂuence

the decision-making process. Consider, for example,

a WVG of three voters, a

, a

, and a

with respective

weights 6, 3, and 1. When the quota for the game is

10, then a coalition consisting of all the three vot-

ers is needed to win the game. Thus, each of the

voters are of equal importance in achieving the win-

ning coalition. Hence, they each have equal power

irrespective of their weight distribution, in that ev-

ery voter is necessary for a win. The three prominent

power indices for measuring agents’ power are the

Shapley-Shubik, Banzhaf, and Deegan-Packel indices

(Matsui and Matsui, 2000). All the three methods as-

sign equal power to the voters in this example.

This paper discusses WVGs and two methods

of manipulating those games, called annexation and

merging (Aziz and Paterson, 2009). In annexation,

a strategic agent, termed an annexer, may alter a

game by taking over the voting weights of some other

agents in the game in order to use the weights in

her favor. As a straightforward example of annexa-

tion, consider when a shareholder buys up the vot-

ing shares of some other shareholders (Machover and

Felsenthal, 2002). We refer to the agents whose vot-

ing shares were bought as the assimilated voters. The

new game consists of the previous agents in the orig-

124

O. Lasisi R. and H. Allan V..

ANNEXATIONS AND MERGING IN WEIGHTED VOTING GAMES - The Extent of Susceptibility of Power Indices.

DOI: 10.5220/0003177201240133

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 124-133

ISBN: 978-989-8425-41-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

inal game whose weights were not annexed by the

strategic agent and the bloc of agent made up of the

annexer and the assimilated voters. The annexer also

incurs some annexation cost to allow purchasing the

votes of the assimilated voters. In this situation, only

the annexer beneﬁts from the annexation as the power

of the bloc in the new game is compared to the power

of the annexer in the original game.

On the other hand, merging is the voluntary co-

ordinated action of would-be manipulators who come

together to form a bloc. The agents in the bloc are

also assumed to be assimilated voters since they can

no more vote as individual voters in the new game,

rather as a bloc. The new game consists of the pre-

vious agents in the original game that are not assim-

ilated as well as the bloc formed by the assimilated

voters. The power of the bloc in the new game is com-

pared to the sum of the individual powers of all mem-

bers of the assimilated bloc in the original game. No

annexation costs occur as individual voters in the bloc

are compensated via power. All the agents in the bloc

beneﬁt from the merging in case of power increase,

having agreed on how to distribute the gains from

their collusion.

In both annexation and merging, strategic agents

anticipate that the value of their power in the new

games to be at least the value of their power in

the original games. (Machover and Felsenthal, 2002)

show that this anticipation of power increase due

to annexation is always achieved by the annexer

when the Shapley-Shubik index is used to compute

power. This is not true for the Banzhaf index as the

power of the annexer can decrease compared to its

power in the original game. For the case of merging

and for both the Shapley-Shubik and Banzhaf indices,

there are situations where the power of the bloc de-

creases compared to the sum of the individual powers

of all members of the assimilated bloc in the original

games.

To date, the more detailed analysis of players

merging into blocs remains unexplored (Aziz and Pa-

terson, 2009). This paper evaluates the susceptibility

to manipulation via annexation and merging in WVGs

of the following power indices: Shapley-Shubik,

Banzhaf, and Deegan-Packel indices. This is the ex-

tent to which strategic agents may gain power with re-

spect to the original games they manipulate. We pro-

vide empirical analysis of susceptibility to annexation

and merging in WVGs among the three indices. The

main results of this paper are the following:

1. For any unanimity WVGs of n agents:

a. Contrary to (Aziz and Paterson, 2009) that for

both Shapley-Shubik and Banzhaf indices it is

advantageous for a player to annex, we show

that this is not true in its entirety. Apart from the

fact that annexation always increases the power

of other agents that are not annexed by the same

factor of increment as the annexer achieved, the

annexer also incurs annexation costs that re-

duce the beneﬁt the agent thought it gained.

b. Using the Shapley-Shubik, Banzhaf, and

Deegan-Packel indices to compute power, the

manipulability of any one index does not dom-

inate the manipulability of other indices.

c. The upper bound on the extent to which a

strategic agent may gain (i.e., the factor of in-

crement) while annexing other agents in the al-

tered game is at most n times the power of the

agent in the original game. The result holds for

the Shapley-Shubik, Banzhaf, and the Deegan-

Packel power indices.

2. The Shapley-Shubik, Banzhaf, and the Deegan-

Packel indices are all highly susceptible to

manipulation via annexation in non unanimity

WVGs. However, the Shapley-Shubik index is the

most susceptible of the three indices.

3. Unlike manipulation via annexation in the non

unanimity WVGs, the Shapley-Shubik, Banzhaf,

and the Deegan-Packel indices are all less sus-

ceptible to manipulation via merging. Again, the

Shapley-Shubik index is the most susceptible of

the three indices.

4. Finally, the Shapley-Shubik index manipulability

dominates that of the Banzhaf index, which in

turn dominates that of the Deegan-Packel index

for both manipulation via annexation and merg-

ing in non unanimity WVGs.

The remainder of the paper is organized as fol-

lows. Section 2 discusses related work. Section 3 pro-

vides the deﬁnitions and notations used in the pa-

per. In Section 4, we provide examples using the three

power indices to illustrate manipulation via annexa-

tion and merging in WVGs. Section 5 considers una-

nimity and non unanimity WVGs. We also provide

evaluation of manipulation via annexation for una-

nimity WVGs. Section 6 provides empirical evalua-

tion of susceptibility of the three power indices to ma-

nipulations via annexation and merging for non una-

nimity WVGs. We conclude in Section 7.

2 RELATED WORK

Weighted voting games and power indices are widely

studied (Matsui and Matsui, 2000; Leech, 2002;

Alonso-Meijide and Bowles, 2005; Bachrach et al.,

ANNEXATIONS AND MERGING IN WEIGHTED VOTING GAMES - The Extent of Susceptibility of Power Indices

125

2008; Aziz and Paterson, 2009). WVGs have many

applications, including economics, political science,

neuroscience, threshold logic, reliability theory, dis-

tributed systems (Aziz et al., 2007), and multia-

gent systems (Bachrach and Elkind, 2008). Prominent

real-life situations where WVGs have found applica-

tions include the United Nations Security Council, the

Electoral College of the United States and the Interna-

tional Monetary Fund (Leech, 2002; Alonso-Meijide

and Bowles, 2005).

The study of WVGs has also necessitated the

need to fairly determine the power of players in a

game. This is because the power of a player in a game

provides information about the relative importance of

that player when compared to other players. To eval-

uate players’ power, prominent power indices such

as Shapley-Shubik, Banzhaf, and Deegan-Packel in-

dices are commonly employed (Matsui and Matsui,

2000). These indices satisfy the axioms that charac-

terize a power index, have gained wide usage in po-

litical arena, and are the main power indices found in

the literature (Laruelle, 1999). These power indices

have been deﬁned on the framework of subsets of

winning coalitions in the game they seek to evalu-

ate. A wide variation in the results they provide can

be observed. This is due to the different deﬁnitions

and methods of computation of the associated subsets

of the winning coalitions. Then, comes the question

of which of the power indices is the most resistant to

manipulation in a WVG. The choice of a power index

depends on a number of factors, namely, the a priori

properties of the index, the axioms characterizing the

index, and the context of decision making process un-

der consideration (Laruelle, 1999).

The three indices we consider measure the in-

ﬂuence of voters differently. There are many situ-

ations where their values are the same for similar

games. However, there exists an important example

of the US federal system while using the Shapley-

Shubik and Banzhaf indices where they do not agree

(Kirsch and Langner, 2010). According to (Laruelle

and Valenciano, 2005), and (Kirsch, 2007), the deci-

sion of which index to use in evaluating a voting situ-

ation is largely dependent on the assumptions about

the voting behavior of the voters. When the voters

are assumed to vote completely independently of each

other, the Banzhaf index has been found to be ap-

propriate. On the other hand, Shapley-Shubik index

should be employed when all voters are inﬂuenced by

a common belief on their choices. Deegan-Packel in-

dex is appealing in that it assigns powers based on

size of the winning coalition, thus giving preference

to smaller coalitions (which may be easier to form).

Under certain assumptions in the WVGs, com-

puting the power indices of voters using any of

Shapley-Shubik, Banzhaf, or Deegan-Packel indices

is NP-hard (Matsui and Matsui, 2000). (Deng and

Papadimitriou, 1994) also show that computing the

Shapley value in WVGs is #P-complete. However,

the power of voters using any of the three indices

can be computed in pseudo-polynomial time by dy-

namic programming (Garey and Johnson, 1979; Mat-

sui and Matsui, 2000). There are also approxima-

tion algorithms for computing the Shapley-Shubik

and Banzhaf power indices (Bachrach et al., 2008).

(Bachrach and Elkind, 2008) have studied a form

of manipulation in WVGs called false name manipu-

lation. In false name manipulation, a strategic agent

may alter a game in anticipation of power increase by

splitting its weight among several false identities that

are not in the original game. They use the Shapley-

Shubik index to evaluate agents’ power and consider

the case when an agent splits into exactly two false

identities. The extent to which agents increase or de-

crease their Shapley power is also bounded. Similar

results using Banzhaf index were obtained by (Aziz

and Paterson, 2009). Furthermore, (Lasisi and Al-

lan, 2010) extends existing work by (Bachrach and

Elkind, 2008), and (Aziz and Paterson, 2009). Their

work empirically considers the effects of false name

manipulation in WVGs when an agent splits into

more than two identities. Results of their experi-

ments suggest that the three indices are susceptible

to false name manipulation in WVGs. However, that

the Deegan-Packel index is more susceptible than the

Shapley-Shubik and Banzhaf indices.

As mentioned in the introduction, very little work

exists on manipulation via annexation and merging

in WVGs, and the more detailed analysis of players

merging into blocs, until now, has remained unex-

plored (Aziz and Paterson, 2009). We discuss some

notable exceptions. (Machover and Felsenthal, 2002),

prove that if a player annexes other players, then the

annexation is always advantageous for the annexerus-

ing the Shapley-Shubik index. The annexation can be

advantageous or disadvantageous using the Banzhaf

index. For the case of merging, and for both the

Shapley-Shubik and Banzhaf indices, merging can be

advantageous or disadvantageous. (Aziz and Pater-

son, 2009) show that for some classes of WVGs, and

for both Shapley-Shubik and Banzhaf indices, it is

disadvantageous for a coalition to merge, while ad-

vantageous for a player to annex. They also prove

some NP-hardness results for annexation and merging

in WVGs. They show that for both Shapley-Shubik

and Banzhaf indices, ﬁnding a beneﬁcial annexation

is NP-hard. Also, determining if there exists a beneﬁ-

cial merge is NP-hard for the Shapley-Shubik index.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

126

(Machover and Felsenthal, 2002), and (Aziz and

Paterson, 2009) have shown that it can be advanta-

geous for strategic agents to engage in annexation or

merging for Shapley-Shubik and Banzhaf indices in

some classes of WVGs. The authors stop short of ad-

dressing the question of upper bounds on the extent

to which strategic agents may gain with respect to the

games they manipulate. In view of this, our work dif-

fer from those of these authors. We extend the work of

(Lasisi and Allan, 2010), as we study the susceptibil-

ity of the three indices to manipulation via annexation

and merging. We empirically consider the extent to

which strategic agents may gain by engaging in such

manipulation and show how the susceptibility among

the indices compares for different WVGs.

3 DEFINITIONS & NOTATIONS

We give the following deﬁnitions and notations used

throughout the paper.

Weighted Voting Game. Let I = {1, ··· , n} be a

set of n agents. Let w = {w

, ··· , w

} be the corre-

sponding positive integer weights of the agents. Let S

be a non empty set of agents. S ⊆ I is a coalition. A

WVG G with quota q involving agents I is deﬁned as

G = [w

, ··· , w

;q]. Denote by w(S), the weight of a

coalition S derived from the summation of the indi-

vidual weights of agents in S i.e., w(S) =

∑

i∈S

. A

coalition, S, wins in the game G if w(S) ≥ q oth-

erwise it loses. q is constrained as follows

w(I) <

q ≤ w(I). Thus, disjoint winning coalitions cannot

emerge.

Simple Voting Game. Each of the coalitions S ⊆ I

has an associated value function v : S → {0, 1}. The

value 1 implies a win for the coalition and 0 a loss. In

the game G, v(S) = 1 if w(S) ≥ q and 0 otherwise.

Dummy and Critical Agents. An agent i ∈ S is

dummy if its weight in S is not needed for S to be a

winning coalition, i.e., w(S\{i}) ≥ q. Otherwise, it is

critical to S, i.e., w(S) ≥ q and w(S\{i}) < q.

Unanimity Weighted Voting Game. A WVG in

which there is a single winning coalition and every

agent is critical to the coalition is unanimity weighted

voting game.

Shapley-Shubik Power Index. The Shapley-

Shubik power index is one of the oldest power

indices and has been used widely to analyze political

power. The index quantiﬁes the marginal contribution

of an agent to the grand coalition. Each agent in a

permutation is given credit for the win if the agents

preceding it do not form a winning coalition but by

adding the agent in question, a winning coalition is

formed. The power index is dependent on the number

of permutations for which an agent is critical. For

the n! permutations of agents used in determining

the Shapley-Shubik index, there exists exactly one

critical agent in each of the permutations. Denote by

Π the set of all permutations of n agents in a WVG G.

Let π ∈ Π deﬁne a one-to-one mapping where π(i) is

the position of the ith agent in the permutation order.

Denote by S

(i), the predecessors of agent i in π, i.e.,

(i) = { j : π( j) < π(i)}. The Shapley-Shubik index,

(G), of agent i in G is given by

(G) =

∑

π∈Π

[v(S

(i) ∪{i}) − v(S

(i))] (1)

Banzhaf Power Index. Another index that has also

gained wide usage in the political arena is the Banzhaf

power index. Unlike the Shapley-Shubik index, its

computation depends on the number of winning coali-

tions in which an agent is critical. There can be more

than one critical agent in a particular winning coali-

tion. The Banzhaf index, β

(G), of agent i in the same

game, G, as above is given by

(G) =

(G)

∑

i∈I

(G)

(2)

where η

(G) is the number of coalitions in which i is

critical in G.

Deegan-Packel Power Index. The Deegan-Packel

power index is also found in the literature for com-

puting power indices. The computation of this power

index for an agent i takes into account both the num-

ber of all the minimal winning coalitions (MWCs) in

the game as well as the sizes of the MWCs having i as

a member (Matsui and Matsui, 2000). Thus, it is more

impressive to be one in three (who elicited the win)

rather than one in ten. A winning coalition C ⊆ I is a

MWC if every proper subset of C is a losing coalition,

i.e., w(C) ≥ q and ∀T ⊂ C, w(T) < q. The Deegan-

Packel power index, γ

(G), of an agent i in G is given

(G) =

|MWC|

∑

S∈MWC

|S|

(3)

where MWC

are the sets of all MWCs in G that in-

clude i.

Susceptibility of Power Index to Manipulation.

Consider a coalition S ⊂ I, let &S deﬁnes a bloc of

assimilated voters formed by agents in S.

ANNEXATIONS AND MERGING IN WEIGHTED VOTING GAMES - The Extent of Susceptibility of Power Indices

127

Annexation : Let Φ be a power index. Denote by

(G), the power of an agent i in a WVG G. Suppose

i alters G by annexing a coalition S. Let G

′

be the

resulting game after the annexation. We say that Φ

is susceptible to manipulation via annexation if there

exists a G

′

, such that Φ

&(S∪{i})

′

) > Φ

(G); the an-

nexation is termed advantageous. If Φ

&(S∪{i})

′

) <

(G), then the annexation is disadvantageous.

Merging : Let Φ be a power index. Denote by

(G), the power of an agent i in a WVG G. Suppose

a coalition, S, alters G by merging into a bloc. Let

′

be the resulting game after the merging. We say

that Φ is susceptible to manipulation via merging if

there exists a G

′

, such that Φ

′

) >

∑

i∈S

(G);

the merging is termed advantageous. If Φ

′

) <

∑

i∈S

(G), then the merging is disadvantageous.

Factor of Increment (Decrement). Let Φ be a

power index. Denote by Φ

(G), the power of an agent

i in a WVG G. Let G

′

be the resulting game when i al-

ters G by manipulation. The factor of increment (resp.

decrement) of the original power from the manipula-

tion is

′

)

(G)

. The value represents an increment (or

gain) if it is greater than 1 and decrement (or loss) if

it is less than 1. The factor of increment provides an

indication of the extent of susceptibility of power in-

dices to manipulation. A higher factor of increment

by a power index in a game indicates that the index is

more susceptible to manipulation in that game.

Domination of Manipulability. Let Φ and Θ be

two different power indices. Denote by Φ

(G) and

(G), the respective power of an agent i in a WVG G

as determined by Φ and Θ. Let i be an annexer. Sup-

pose the corresponding power of the agent in a new

game G

′

when i alters G by assimilating agents S

are Φ

&(S∪{i})

′

) and Θ

&(S∪{i})

′

). We say that the

manipulability of one index say Φ

′

, dominates the

manipulability of another index Θ

′

for a particu-

lar game G, if the factor by which i gain in Φ is

greater than the factor by which it gain in Θ, i.e.,

&(S∪{i})

′

)

(G)

&(S∪{i})

′

)

(G)

, and hence, Φ is more sus-

ceptible to manipulation than Θ in G. The domination

of manipulability can be similarly deﬁne for manipu-

lation via merging.

4 ANNEXATIONS & MERGING

This section provides examples illustrating manipula-

tion via annexation and merging in WVGs. The power

of the strategic agents, i.e., the annexer or the bloc of

manipulators, and the factor of increment (decrement)

are also summarized in a table for each example using

the three power indices.

4.1 Manipulation via Annexation

Example 1. Annexation Advantageous. Let G =

[5, 8, 3, 3, 4, 2, 4;18] be a WVG. The assimilated

agents are shown in bold, with agent 1 being the an-

nexer. In the original game, the Deegan-Packel in-

dex of the annexer is γ

(G) = 0.1722. In the new

game, G

′

= [9, 8, 3, 3, 2, 4;18], its Deegan-Packel in-

dex is γ

′

) = 0.2604, a factor of increase of 1.51.

Table 1: The annexer power in the original

game G = [5, 8, 3, 3, 4, 2, 4;18], the altered game

′

= [9, 8, 3,3, 2, 4;18], and the factor of increment

for the three indices.

Power Index G G

′

Factor

Shapley-Shubik 0.1714 0.3500 2.04

Banzhaf 0.1712 0.3400 1.99

Deegan-Packel 0.1722 0.2604 1.51

Example 2. Annexation Disadvantageous. Let

G = [8, 9, 9, 5, 7, 3, 9;29] be a WVG. The assimilated

agents are shown in bold, with agent 1 being the an-

nexer. In the original game, the Deegan-Packel index

of the annexer is γ

(G) = 0.1711. In the new game,

′

= [11, 9, 9, 5, 7, 9;29], its Deegan-Packel index is

′

) = 0.1591, a factor of decrease of 0.93.

Table 2: The annexer power in the original

game G = [8, 9, 9, 5, 7, 3, 9;29], the altered game

′

= [11, 9, 9, 5, 7, 9;29], and the factor of increment

(decrement) for the three indices.

Power Index G G

′

Factor

Shapley-Shubik 0.1786 0.2167 1.21

Banzhaf 0.1774 0.2167 1.22

Deegan-Packel 0.1711 0.1591 0.93

4.2 Manipulation via Merging

Example 3. Merging Advantageous. Let G =

[4, 2, 1, 1, 8, 7, 4;17] be a WVG. The assimilated

agents are shown in bold. In the original game, the

Deegan-Packel indices of these agents are, γ

(G) =

0.0926, γ

(G) = 0.1889, and γ

(G) = 0.1704. Their

cummulative power is 0.4519. In the new game, G

′

[13, 4, 1, 1, 8;17], the Deegan-Packel index of the bloc

is γ

′

) = 0.5000, a factor of increase of 1.11.

Example 4. Merging Disadvantageous. Let G =

[5, 8, 3, 4, 9, 1, 5;30] be a WVG. The assimilated

agents are shown in bold. In the original game, the

Deegan-Packel indices of these agents are, γ

(G) =

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

128

Table 3: The cummulaive power of the assimilated agents

in the original game G = [4, 2, 1, 1, 8, 7, 4;17], the power of

the bloc in the altered game G

′

= [13, 4, 1, 1, 8;17], and the

factor of increment for the three indices.

Power Index G G

′

Factor

Shapley-Shubik 0.4881 0.6667 1.37

Banzhaf 0.4851 0.6000 1.24

Deegan-Packel 0.4519 0.5000 1.11

0.1833, γ

(G) = 0.1333, and γ

(G) = 0.1417. Their

cummulative power is 0.5083. In the new game, G

′

[22, 5, 3, 4, 1;30], the Deegan-Packel index of the bloc

is γ

′

) = 0.3056, a factor of decrease of 0.60.

Table 4: The cummulaive power of the strategic agents in

the original game G = [5, 8, 3, 4, 9, 1, 5;30], the power of the

bloc in the altered game G

′

= [22, 5, 3, 4, 1;30], and the fac-

tor of decrement for the three indices.

Power Index G G

′

Factor

Shapley-Shubik 0.6762 0.4667 0.69

Banzhaf 0.5789 0.3684 0.64

Deegan-Packel 0.5083 0.3056 0.60

5 WEIGHTED VOTING GAMES

This section considers manipulatons via annexation

and merging for both unanimity and non unanim-

ity WVGs. For the sake of simplicity in our discus-

sion, we assume that for the case of manipulation

via annexation, the annexer has enough resources to

cover the annexation costs for all the agents it an-

nexes. Also, we assume that only one of the agents

is engaging in the annexation at a time. However, we

are not oblivious of the fact that other agents also

have similar motivations to engage in annexation in

anticipation of power increase. For the case of manip-

ulation via merging, we assume that the assimilated

agents in the bloc can easily distribute the gains from

their collusion among themselves in a fair and stable

way. Thus, making them agree to engage in the ma-

nipulation if it is proﬁtable.

5.1 Unanimity Weighted Voting Games

We recall that a WVG in which there is a single win-

ning coalition and every agent is critical to the coali-

tion is unanimity WVG. (Aziz and Paterson, 2009)

have shown that for unanimity WVGs and for both the

Shapley-Shubik and Banzhaf indices: it is disadvan-

tageous for a coalition to merge and advantageous

for a player to annex other players. We observe that

these results naturally extend to the Deegan-Packel

index too. This is because for unanimity WVGs, the

deﬁnitions of the Shapley-Shubik, Banzhaf, and the

Deegan-Packel indices using Formulas 1, 2, and 3,

respectively, are equivalent. In fact, the power of all

agents in any unanimity WVGs is the same for the

three indices. In view of the annexation result of (Aziz

and Paterson, 2009) above, and the fact that strategic

agents are interested in annexations and merging that

improve their power, we consider only manipulation

via annexation for the unanimity WVGs.

Note that (Aziz and Paterson, 2009) have not con-

sidered the bounds on the extent to which strate-

gic agents may gain with respect to games they ma-

nipulate. This is important as it provides motiva-

tions for strategic agents to engage in manipulation

when derivable gains are appreciable. Apart from this,

the gains or the factor of increments show the ex-

tent of susceptibility to manipulation and provide a

measure of domination of manipulability among the

indices. The magnitude of this gain for unanimity

WVGs, as we shall see shortly, depends on the num-

ber of agents in the original game, the number of

agents the annexer is able to annex, as well as the

annexation costs. Example 5 illustrates a unanim-

ity WVG where an annexer appears to achieve three

times its original power annexing other agents.

Example 5. Annexation Advantageous:

Unanimity WVGs. Consider G =

[7, 6, 9, 2, 5, 3, 1, 1, 8, 2, 2, 8, 4, 9, 6;73], a unanim-

ity WVG of 15 agents. The Deegan-Packel index

of any agent in the game is 0.0667. Suppose the

ﬁrst agent with weight 7, alters G by annexing

the next ten agents in the game. The new game

′

= [46, 8, 4, 9, 6;73]. The annexer has improved its

weight to 46. The Deegan-Packel index of the annexer

in G

′

is γ

′

) = 0.2000. The agent beneﬁts from the

annexation and increases its power by a factor of 3.

Table 5: The annexer power in the original game

G = [7, 6, 9, 2, 5, 3, 1, 1, 8, 2, 2, 8,4, 9, 6;73], the altered game

′

= [46, 8, 4, 9, 6;73, and the factor of increment for the

three indices.

Power Index G G

′

Factor

Shapley-Shubik 0.0667 0.2000 3.00

Banzhaf 0.0667 0.2000 3.00

Deegan-Packel 0.0667 0.2000 3.00

It appears that the annexer has achieved a gain of

three times its original power while annexing other

agents, but this is not true in its entirety. We provide

the following arguments. Since the original and the

altered games are unanimity, the power of all agents

in each game is the same. While the annexer has im-

provedits weight, and consequentlyits power by three

ANNEXATIONS AND MERGING IN WEIGHTED VOTING GAMES - The Extent of Susceptibility of Power Indices

129

times its original power, other agents that were not as-

similated have also had their power increased by the

same factor, even though their weights in the origi-

nal and altered games remain the same. Clearly, these

agents do not incur any cost like the annexer whose

improved weight and power must have been achieved

at annexation costs. The annexation costs reduce the

beneﬁts the agent thought it gained, making the an-

nexer’s beneﬁt worse than the beneﬁts of other agents

not engaging in annexation. This weakens (Aziz and

Paterson, 2009) result that for unanimity WVG and

for both Shapley-Shubik and Banzhaf indices it is ad-

vantageous for a player to annex.

Now, suppose we assume that the annexer still ac-

crues some gains even after the application of the an-

nexation costs, then these gains are the same for the

three indices. We see that the extents of susceptibil-

ity to manipulation among the three indices are the

same. Hence, for any unanimity WVGs, the manipu-

lability of any one index does not dominate the ma-

nipulability of other indices.

Finally, the generalization of the upper bound on

the extent to which a strategic agent may gain with re-

spect to games it manipulate in any unanimity WVGs

follows from (Aziz and Paterson, 2009). For any una-

nimity WVG of n agents, the power of each agent

. If a strategic agent annexes k − 1 other agents,

the power of the strategic agent as well as that of the

other agents in the new game is

n−k+1

. Hence, the fac-

tor of increment for each agent is

n−k+1

. This factor

of increment is the same for the three indices. When

k = 1, (i.e., the strategic agent is not annexing any

other agent), then the factor of increment is 1, and

this implies the same game we started with. Whereas,

when k = n, the strategic agent is able to annex the

remaining n− 1 agents in the original game, then the

factor of increment is n times the power of the agent

in the original game. This is the upper bound on the

extent to which a strategic agent may achieve while

annexing other agents in any unanimity WVG. This

bound holds for the three power indices.

5.2 Non Unanimity Weighted Voting

Games

Manipulation by annexation and merging in the gen-

eral case of WVGs is more interesting as it pro-

vides more complex and realistic scenarios that are

not well-understood. As the structure of the WVGs

changes due to annexation and merging, the number

of winning coalitions as well as the minimal winning

coalitions in the games also changes.

Consider a WVG G of I agents with quota q. If

any agent i ∈ I has weight w

≥ q, then the agent

will always win without forming coalitions with other

agents. The more interesting games we consider are

those for which w

< q, and such that q satisﬁes the in-

equality q < w(I) − m, where m is at least the weight

of exactly one of the agents in the game. When the

grand coalition (i.e., a coalition of all the agents)

emerges, it will always contain some agents that are

not critical in the coalition. It is easy to see that all

the winning coalitions in this type of games are non

unanimity; hence, all the games here are non una-

nimity WVGs. In order to evaluate the behaviors of

the indices for non unanimity WVGs, we conduct

experiments to evaluate the effects of manipulation

when a strategic agent annexes some other agents in

the games or when some manipulators merge to form

blocs using each of the three indices. The simulation

environment and simulation results are discussed in

Subsections 6.1 and 6.2, respectively.

6 EXPERIMENTS

This section provides detail descriptions of the sim-

ulation environment used for the conduct of experi-

ments, and analysis of the experimental results used

for the evaluation of the effects of manipulation via

annexation and merging in non unanimity WVGs.

6.1 Simulation Environment

We perform experiments to evaluate the effects of

manipulation via annexation and merging by agents

using each of the three power indices. To facilitate

comparison, we have 15 agents in each of the origi-

nal WVGs. The weights of our agents in these games

are chosen so that no weight is larger than ten. These

weights are reﬂective of realistic voting procedures

as the weights of agents in real votings are not too

large (Bachrach and Elkind, 2008). When creating a

new game, all agents are randomly assigned weights

and the quota of the game is also generated to satisfy

the inequality of non unanimity WVGs of Subsection

5.2. The least possible weight for any agent is one.

For the case of manipulation via annexation, we

randomly generate WVGs and assume that only the

ﬁrst agent in the game is engaging in the manip-

ulation, i.e., the annexer. Then, we determine the

three power indices (i.e., Shapley-Shubik, Banzhaf,

and Deegan-Packel power index) of this agent in the

game. After this, we consider annexation of at least

one agent in the game by the annexer, while the

weights of other agents not annexed remain the same

in the altered games. For a particular game, the an-

nexer may annex 1 ≤ i ≤ 10 other agents; we refer to

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

130

i as the bloc size. The bloc size is randomly generated

for each game. The weight of the annexer in the new

game is the sum of the weights of the agents it an-

nexed plus the annexer’s initial weight in the original

game. We compute the new power index of the an-

nexer in the altered games next. Now, we determine

the factor of increment by which the annexer gains or

loses in the manipulation for the corresponding bloc

sizes i, in the range 1 ≤ i ≤ 10.

We use the same procedure as described above for

the case of manipulation via merging with the fol-

lowing modiﬁcations. Since merging requires coor-

dinated action of the manipulators, we randomly se-

lect strategic agents among the agents in the WVGs

to form the blocs of manipulators. The bloc size 2 ≤

i ≤ 10, for mergng is also randomly generated for

each game. The weight of a bloc in a new game is

the sum of the weights of the assimilated agents in

the bloc. The bloc participates in the new game as

though a single agent. We compute the new power in-

dex of the bloc in the altered games next. Again, we

determine the factor of increment by which the bloc

gains or loses in the manipulation for the correspond-

ing bloc sizes. Unlike in annexation, the power of the

bloc is compared with the sum of the original powers

of the individual agents in the bloc.

For our study, we generate 2, 000 original WVGs

for various bloc sizes and allow manipulation by the

annexer or the bloc of manipulators. For each game,

we compute the factor of increment by which the an-

nexer or the bloc gains or loses. Finally, we compute

the average value of these factors of increment overall

the games for each bloc size. We use 2, 000 WVGs in

order to capture a variety of games that are represen-

tative of the non unanimity WVGs and to minimize

the standard deviation from the true factors when we

compute the average values. The average value of the

factors of increment provides the extent of suscepti-

bility to manipulation by each of the three indices. We

estimate the domination of manipulability among the

three indices by comparing their average factors of in-

crement simultaneously in similar games.

6.2 Simulation Results

We present the results of our simulations. Experi-

ments conﬁrm the existence of advantageous annexa-

tion and merging for the non unanimity weighted vot-

ing games when agents engage in manipulation us-

ing the three indices. However, the extent to which

agents gain varies with both annexation and merging,

and among the indices.

Consider manipulation by annexation in non una-

nimity WVGs ﬁrst. We provide a comparison of sus-

ceptibility to manipulation among the three indices by

comparing the population of factors of increment at-

tained by strategic agents in different games for each

of the indices. A summary of susceptibility to ma-

nipulation among the three indices for 2, 000 WVGs

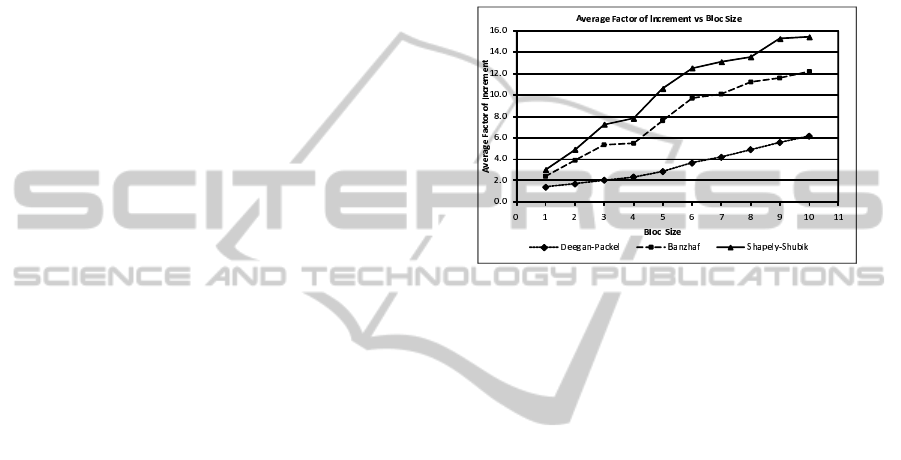
is shown in Figure 1. The x-axis indicates the bloc

sizes while the y-axis is the average factor of incre-

ment achieved by agents in the 2, 000 WVGs for cor-

responding bloc sizes.

Figure 1: Susceptibility to Manipulation via Annexation

among the Shapley-Shubik, Banzhaf, and Deegan-Packel

indices for Non Unanimity WVGs.

The effect of manipulation via annexation is pro-

nounced for the three power indices, as all the in-

dices are highly susceptible to manipulation. How-

ever, the higher susceptibility of the Shapley-Shubik

and Banzhaf indices than the Deegan-Packel index

can be observed from Figure 1. While the aver-

age factor of increment for manipulation rapidly

grows with the bloc sizes for the Shapley-Shubik

and Banzhaf indices, that of the Deegan-Packel index

grows more slowly. By the average factor of incre-

ment, the Shapley-Shubik index manipulability dom-

inates that of Banzhaf index, which in turn dominates

that of Deegan-Packel index. Also, there is a positive

correlation between the average factor of increment

and the bloc sizes for the three indices. The average

factor of increment increases with the bloc sizes.

This analysis suggests that the Shapley-Shubik

and Banzhaf power indices are more susceptible to

manipulation via annexation than the Deegan-Packel

power index. Since all the three power indices are

susceptible to manipulation via annexation, this pro-

vides some motivation for strategic agents to gener-

ally engage in such manipulation for the non unanim-

ity WVGs when they are being evaluated using any

of the three power indices, and in particular, when the

Shapley-Shubik index is employed.

Figure 2 provides similar results for the non una-

nimity WVGs when there are coordinated efforts

among manipulators that culminate in merging. We

ANNEXATIONS AND MERGING IN WEIGHTED VOTING GAMES - The Extent of Susceptibility of Power Indices

131

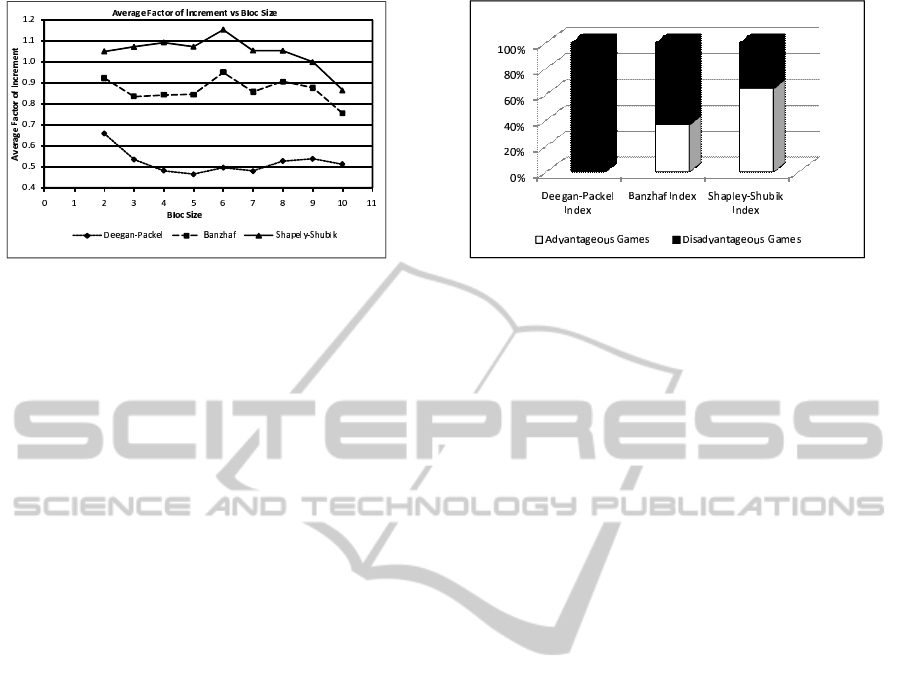
Figure 2: Susceptibility to Manipulation via Merging

among the Shapley-Shubik, Banzhaf, and Deegan-Packel

indices for Non Unanimity WVGs.

again compare susceptibility to manipulation among

the three power indices. Unlike manipulation via

annexation, only the Shapley-Shubik index appears

to be susceptible to manipulation for this type of

game. Also, there appears not to be any correlation

between the average factor of increment achieved by

the bloc of manipulatorsand the bloc size for the three

power indices. Thus, it is unclear to the would-be ma-

nipulators what bloc size would be advantageous or

disadvantageous to the bloc, and to what extent.

It is easy to see from the trends of the three power

indices in Figure 2, that, using the average factor of

increment over the games we consider, the Shapley-

Shubik index manipulability dominates that of the

Banzhaf index, which in turn dominates that of the

Deegan-Packel index. Another positive result that is

observable from Figure 2 is that the highest aver-

age factor of increment for the three power indices

is less than a factor of 1.2 as compared to a factor

of 15, found for the Shapley-Shubik index, 12 for

the Banzhaf index, and 6 for the Deegan-Packel in-

dex under the manipulation via annexation. See Fig-

ure 1. Again, examination of the 2, 000 WVGs reveals

that many of the games are advantageous for Shapley-

Shubik index, few for the Banzhaf index, and virtually

none for the Deegan-Packel index. Figure 3 shows

the percentage of advantageous and disadvantageous

games for manipulation via merging among the three

indices for the 2, 000 non unanimity WVGs. Even for

the cases where the games are advantageous for the

three indices, the factor of increment achieved by the

blocs of manipulators are not very high, and in all

cases are less than a factor of 2.

The analysis suggests that the the Shapley-Shubik

index is more susceptible to manipulation via merging

than the Banzhaf and Deegan-Packel power indices

for non unanimity WVGs, even though the factor of

increment is not high. Now, since only the Shapley-

Shubik index is more susceptible to manipulations via

Figure 3: Percentage of Advantageous and Disadvanta-

geous Games for Manipulation via Merging among the

three indices for 2, 000 Non Unanimity WVGs.

merging, and also, since the factor by which the bloc

of manipulators gains is very low, we suspect that this

may provide less motivation for strategic agents to

generally engage in manipulation via merging for the

non unanimity WVGs when they are being evaluated

using any of the three power indices, and in particular,

when the Deegan-Packel index is employed.

7 CONCLUSIONS

We have considered the effects of manipulation by

annexation and merging in weighted voting games

focusing on the indices used in evaluating agents’

power in such games. The following prominent

power indices are used to evaluate the power of

agents: Shapley-Shubik, Banzhaf, and the Deegan-

Packelindices. We consider the extent to which strate-

gic agents may gain by engaging in such manipula-

tion and show how the susceptibility among the three

indices compares for unanimity and non unanimity

weighted voting games.

For unanimity weighted voting games of n agents,

we show that apart from the fact that annexation al-

ways increases the power of other agents that are

not annexed by the same factor of increment as the

annexer achieved, the annexer also incurs annexa-

tion costs that reduce the beneﬁt the agent thought

it gained, making the annexer’s beneﬁt worse than

the beneﬁts of other agents not engaging in annexa-

tion. Also, for the three power indices, the manipula-

bility of any one index does not dominate the manipu-

lability of other indices for manipulation via annexa-

tion. Finally, the upper bound on the extent to which a

strategic agent may gain while annexing other agents

in the altered game is at most n times the power of the

agent in the original game. This bound holds for the

three power indices.

For non unanimity weighted voting games, we

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

132

show that the games are less vulnerable to manip-

ulation via merging, while they are extremely vul-

nerable to manipulation via annexation for the three

power indices. Also, while the factor of increment

from manipulation grows with bloc sizes for manip-

ulation via annexation, there exists no correlation be-

tween the factor of increment and the bloc size for

manipulation via merging. Finally, we show that the

Shapley-Shubik index manipulability dominates that

of the Banzhaf index, which in turn dominates that

of the Deegan-Packel index for both manipulation via

annexation and merging. Hence, the Shapley-Shubik

index is more susceptible to manipulation via an-

nexation and merging than the Banzhaf and Deegan-

Packel indices, with Deegan-Packel index being the

least susceptible among the indices.

We have some comments regarding these re-

sults. First, we found that our results of manipula-

tion via annexation and merging for non unanimity

weighted voting games are consistent with those of

(Lasisi and Allan, 2010). They consider false name

manipulation in weighted voting games. The manip-

ulation allows an agent to have more power over

the outcomes of the games by splitting into multiple

names and distributing its weights across all associ-

ated names. They showed that for the non unanimity

weighted voting games; the Deegan-Packel index is

more susceptible to false name manipulation than the

Banzhaf and Shapley-Shubik indices, with Shapley-

Shubik index being the least susceptible among the

three indices. The implication of this consistency is

that a scenario where splitting by a strategic agent is

disadvantageous corresponds to a scenario where it is

advantageous for several strategic agents to merge.

Second, we have assumed throughout this paper

that for the case of manipulation via merging, the as-

similated agents in the bloc can easily distribute the

gains from their collusion among themselves in a fair

and stable way. Thus, making them agree to engage in

the manipulation if it is proﬁtable. This assumption is

strong. Even at that, we see that all the three indices

are less vulnerable to manipulation via merging.

ACKNOWLEDGEMENTS

This work is supported by NSF research grant

#0812039 entitled “Coalition Formation with Agent

Leadership”.

REFERENCES

Alonso-Meijide, J. M. and Bowles, C. (2005). Generating

functions for coalitional power indices:an application

to the imf. Annals of Operations Research, 137:21–

44.

Aziz, H. and Paterson, M. (2009). False-name manipu-

lations in weighted voting games: splitting, merging

and annexation. In Proceedings of the Intl. Joint Conf.

on Autonomous Agents and Multiagent Systems, pages

409–416, Budapest, Hungary.

Aziz, H., Paterson, M., and Leech, D. (2007). Combina-

torial and computational aspects of multiple weighted

voting games. The Warwick Economics Research Pa-

per Series (TWERPS) 823, University of Warwick, De-

partment of Economics.

Bachrach, Y. and Elkind, E. (2008). Divide and con-

quer: false-name manipulations in weighted voting

games. In 7th Intl. Conf. on Autonomous Agents and

Multiagent Systems, pages 975–982, Estoril, Portugal.

Bachrach, Y., Markakis, E., Procaccia, A. D., Rosenschein,

J. S., and Saberi, A. (2008). Approximating power

indices. In 7th Intl. Conf. on Autonomous Agents and

Multiagent Systems, pages 943–950, Estoril, Portugal.

Deng, X. and Papadimitriou, C. H. (1994). On the complex-

ity of cooperative solution concepts. Mathematics of

Operations Research, 19(2):257–266.

Garey, M. and Johnson, D. (1979). Computers and

Intractability: A Guide to the Theory of NP-

Completeness. W.H. Freeman, San Fransisco.

Kirsch, W. (2007). On penrose’s squareroot law and be-

yond. Homo Oeconomicus, 24(3,4):357–380.

Kirsch, W. and Langner, J. (2010). Power indices and min-

imal winning coalitions. Social Choice and Welfare,

34(1):33–46.

Laruelle, A. (1999). On the choice of a power index.

Instituto Valenciano de Investigaciones Economicas,

2103:99–10.

Laruelle, A. and Valenciano, F. (2005). Assessing success

and decisiveness in voting situations. Social Choice

and Welfare, 24(1):171–197.

Lasisi, R. O. and Allan, V. H. (2010). False name manip-

ulations in weighted voting games: Susceptibility of

power indices. In proceedings of the 13th Workshop

on Trust in Agents Societies of the Autonomous Agents

and Multiagents Systems Conference, pages 139–150,

Toronto, Canada.

Leech, D. (2002). Voting power in the governance of the in-

ternational monetary fund. Annals of Operations Re-

search, 109(1):375–397.

Levchenkova, L. and Levchenkov, V. (2002). A power index

in weighted voting systems. Journal of Computational

Mathematics and Modelling, 13(4):375–392.

Machover, M. and Felsenthal, D. S. (2002). Annexation

and alliances: When are blocs advantageous a priori.

Social Choice and Welfare, 19(2):295–312.

Matsui, T. and Matsui, Y. (2000). A survey of algorithms

for calculating power indices of weighted majority

games. Journal of the Operations Research Society

of Japan, 43(1).

ANNEXATIONS AND MERGING IN WEIGHTED VOTING GAMES - The Extent of Susceptibility of Power Indices

133