
ECG P-WAVE SMOOTHING AND DENOISING BY QUADRATIC
VARIATION REDUCTION
Antonio Fasano
1
, Valeria Villani
1,2
, Luca Vollero
1
and Federica Censi
2
1
Universit`a Campus Bio-Medico di Roma, Rome, Italy
2
Department of Technology and Health, Italian National Institute of Health, Rome, Italy
Keywords:
ECG, P-wave, Atrial fibrillation, Smoothing, Denoising, Quadratic variation, Convex optimization.
Abstract:
Atrial fibrillation is the most common persistent cardiac arrhythmia and it is characterized by a disorganized
atrial electrical activity. Its occurrence can be detected, and even predicted, through P-waves time-domain and
morphological analysis in ECG tracings. Given the low signal-to-noise ratio associated to P-waves, such anal-
ysis are possible if noise and artifacts are effectively filtered out from P-waves. In this paper a novel smoothing
and denoising algorithm for P-waves is proposed. The algorithm is solution to a convex optimization problem.
Smoothing and denoising are achieved reducing the quadratic variation of the measured P-waves. Simulation
results confirm the effectiveness of the approach and show that the proposed algorithm is remarkably good
at smoothing and denoising P-waves. The achieved SNR gain exceeds 15 dB for input SNR below 6 dB.
Moreover the proposed algorithm has a computational complexity that is linear in the size of the vector to be
processed. This property makes it suitable also for real-time applications.
1 INTRODUCTION
Atrial fibrillation (AF) is a cardiac arrhythmia charac-
terized by disorganized atrial electrical activity caus-
ing loss of effective contraction. AF is the most com-
mon persistent cardiac arrhythmia and it is also the
most common cause of arrhythmia-related hospital-
izations (Feinberg et al., 1995; Go et al., 2001). It has
an enormous social impact because of its very high
incidence and its clinical consequences. Moreover, it
is often difficult to diagnose and its management is
not optimized. The incidence of AF increases with
age and given the life expectancies increasing in both
developed and developing countries, AF is projected
to become an important burden on most health care
systems (McBride et al., 2008).
AF is the most common arrhythmia in the west-
ern countries, it is responsible for 70 to 100 thousand
strokes per year in the US and is independently asso-
ciated with up to 1.9-fold increase in the risk of death
(Benjamin et al., 1998).
AF is also associated with extensive atrial struc-
tural, contractile, and electrophysiological remodel-
ing, which can sustain AF itself (Nattel et al., 2008).
Current pharmacological treatments of AF present
some limits because they can be ventricular proar-
rhythmic and not able to prevent recurrences of AF.
A great deal of research on AF has focused on the
identification of factors that can predict its first occur-
rence or recurrence. This could help in defining the
best treatment in individual patients.
Promising results have been obtained from ECG
signal processing, particularly from the analysis of
P-waves. Electrocardiographic characteristics of AF
have proven to be helpful in identifying patients at
risk (Dilaveris and Gialafos, 2002; Platonov et al.,
2000; Carlson et al., 2001; Bayes de Luna et al.,
1999).
Prolonged and highly variable P-waves have been
observed in patients prone to AF. Time-domain and
morphological characteristics of P-waves from sur-
face ECG recordings turned out to significantly dis-
tinguish patients at risk of AF (Bayes de Luna et al.,
1999; Perez et al., 2009).
Most of these studies rely on measurements based
on visual inspection; however, computerized auto-
matic analyses can now be performed and have been
recently introduced to estimate P-wave duration and
morphological indices (Censi et al., 2007; Censi et al.,
2008).
Due to the low signal-to-noise ratio associated
with P-waves, this portion of ECG signal is usu-
ally analyzed performing signal averaging in order
to build a P-wave template. Then, waves duration
289
Fasano A., Villani V., Vollero L. and Censi F..
ECG P-WAVE SMOOTHING AND DENOISING BY QUADRATIC VARIATION REDUCTION.
DOI: 10.5220/0003169202890294
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 289-294
ISBN: 978-989-8425-35-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

and morphological features are extracted from this
template. The unavoidable drawback of this ap-
proach is that some information is lost in the aver-
aging operation. Each P-wave provides important in-
formation about the correspondingdepolarization pat-
tern throughout the atrial substrate. Thus, tracking
changes between consecutive P-waves turns out to be
extremely important in improving the understanding
of the pathophysiological mechanisms of atrial sub-
strates predisposing to AF.
However, the analysis of the temporal variabil-
ity of consecutive P-waves is possible only if reliable
beat-to-beat P-waves are available. This is attainable
only if noise and artifacts are effectively filtered out
from each single P-wave.
The aim of this investigation is to propose a novel
method to smooth and denoise P-waves extracted
from high-resolution DC-coupled ECG recordings, in
order to improve the signal-to-noise ratio (SNR) of
each single P-wave.
2 RATIONALE
From the previous section, it is evident that the abil-
ity to conduct a meaningful analysis of predisposing
factors to AF strongly depends on the availability of
reliable P-waves. In this regard, P-waves are reliable
if the detrimental effects of noise and artifacts are re-
duced to an acceptable level.
In this section we propose an algorithm that is par-
ticularly effective for P-waves smoothing and denois-
ing. It is based on the following idea. The measured
P-wave is affected by noise and artifacts whose ef-
fect is to introduce additional “variability” into the
observed P-wave with respect to the true one. Thus,
provided that we introduce a suitable index of vari-
ability, smoothing and denoising can be performed by
searching for a version of the P-wave that is close, in
some sense, to the observed one, but has less “vari-
ability”. We make this idea precise in the following.
Denote by z
z
z = [z
1
···z
n
]
T
the vector collecting n
samples of a noisy P-wave extracted from an ECG
tracing. The variability of a generic vector can be
quantified introducing the following
Definition 1. Given a vector x
x
x = [x
1
···x
n
]
T
∈ R
n
, the
quadratic variation of x
x
x is defined as
[x
x
x]
.
=
n−1
∑
k=1
(x
k
− x
k+1
)
2
(1)
and is denoted by [x
x
x].
The quadratic variation is a well-known property
used in the analysis of stochastic processes (Shreve,
2004). However, in this context we consider it as a
function of deterministic or random vectors.
Introducing the (n− 1) × n matrix
D
D
D =
1 −1 0 . . . 0
0 1 −1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0
0 . . . 0 1 −1
, (2)
the quadratic variation of x
x
x can be expressed as
[x
x
x] = kD
D
Dx
x
xk
2
, (3)
where k·k denotes the Euclidean norm.
The quadratic variation is a consistent index of
variability and its use is motivated by the following
property. For vectors affected by additive noise, on
average it does not decrease and moreover it is an
increasing function of noise variances. In fact, let
x
x
x = x
x
x
0
+ w
w
w, where x
x
x
0
is a deterministic vector and
w
w
w = [w
1
···w
n
] is a zero-mean random vector with co-
variance matrix K
K
K
w
= E
w
w
ww
w
w
T
. We do not make any
assumption about the distribution of w
w
w, so the follow-
ing considerations hold regardless of it. Computing
the averaged quadratic variation of x
x
x we get
E
n
kD
D
Dx
x
xk
2
o
= kD
D
Dx
x
x
0
k
2
+ E
tr
D
D
Dw
w
ww
w
w
T
D
D
D
T
= kD
D
Dx
x
x
0
k
2
+ tr
D
D
DK
K
K
w
D
D
D
T
(4)
where, in the first equality, we have exploited the in-
variance of the trace under cyclic permutations. Note
that tr
D
D
DK
K
K
w
D
D
D
T
≥ 0, since it is the trace of a positive
semidefinite matrix (Horn and Johnson, 1990), but in
all practical cases the inequality is strict. In fact, we
have
tr
D
D
DK
K
K
w
D
D
D
T
=
n−1
∑
k=1
E
n
(w
k
− w
k+1
)
2
o
=
n−1
∑
k=1
σ
2
k
+ σ
2
k+1
− 2σ
k,k+1
(5)
where σ
2
k
= E
w
2
k
and σ
k,k+1
= E {w
k
w
k+1
}. From
(5) it follows that tr
D
D
D
T
D
D
DK
K
K
w
= 0 if and only if allthe
components of the noise vector w
w
w are almost surely
equal
1
and that E
n
kD
D
Dx
x
xk
2
o
is an increasing function
of noise variances.
For example, in typical scenarios of ECG trac-
ings w
w
w = m
m
m + a
a
a, where m
m
m is due to white Gaussian
noise whereas a
a
a is due to the residual 50Hz or 60Hz
power-line noise. We may assume m
m
m ∼ N
0
0
0, σ
2
m
I
I
I
and a
a
a = [a
1
···a
n
] vector of samples from a harmonic
process, i.e., a
k
= Acos
h
2π
f
0
F
c
k+ φ
i
, with A and φ
1
That is w
1
= w
2
= · · · = w
n
with probability 1.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
290

independent, φ uniformly distributed in [0, 2π), f
0
∈
{50Hz, 60Hz} and F
c
being the sampling frequency.
Moreover m
m
m and a
a
a are independent. In this case it is
easy to verify that
tr
D
D
DK
K
K
w
D
D
D
T
=
= 2(n− 1)
σ
2
m
+ 2E
A
2
sin
2
π
f
0
F
c
=
2kx
x
x
0
k
2
(n− 1)
n
1
SNR
+
4
SIR
sin
2
π
f
0
F
c
(6)
where SNR =
kx
x
x
0
k
2
nσ
2
m
denotes the signal-to-noise ra-
tio and SIR =
2kx
x
x
0
k
2
nE
{
A
2
}
is the signal-to-interference ra-
tio, considering the power-line noise as interference.
From (6) it is evident that the average quadratic vari-
ation is a decreasing function of SNR and SIR.
In the following section we devise an efficient
smoothing algorithm for P-waves exploiting the con-
cept of quadratic variation.
3 SMOOTHING P-WAVES
In this section we denote by p
p
p the vector collecting
samples from the measured P-wave, the one that is
affected by noise and artifacts, and by x
x
x the corre-
sponding vector after smoothing. Following the line
of reasoning presented in the previous section, we de-
termine x
x
x solving the following optimization problem
minimize kx
x
x− p
p
pk
2
subject to kD
D
Dx
x
xk
2
≤ a
(7)
where D
D
D is defined in (2) and a is a positive con-
stant that controls the degree of smoothness for p
p
p.
Its value is chosen in accordance with the peculiar-
ity of the problem and satisfies a < kD
D
Dp
p
pk
2
in order
to avoid trivial solutions.
2
Note that we do not need
to know in advance the appropriate value for a in any
particular problem. In fact, as it will be clear later,
the solution to the optimization problem (7) can be
expressed in terms of a parameter that controls the
degree of smoothness, i.e., the quadratic variation of
the solution, and that is related to the value of a in (7).
In this way, smoothing can be performed without car-
ing about a in the constraint kD
D
Dx
x
xk
2
≤ a, and reducing
parametrically the quadratic variation of the solution
to the desired level. In general, the optimal value for
the controlling parameter can be found, as the one that
entails the maximum SNR gain.
2
When a ≥ kD
D
Dp
p
pk
2
the solution is x
x
x = p
p
p and no smooth-
ing is performed.
Let us consider (7) in more detail. It is a convex
optimization problem, since both the objective func-
tion and the inequality constraint are convex. As a
consequence, any locally optimal point is also glob-
ally optimal and Karush-Kuhn-Tucker (KKT) condi-
tions provide necessary and sufficient conditions for
optimality (Boyd and Vandenberghe, 2004). More-
over, since the objective function is strictly convex
and the problem is feasible the solution exists and is
unique. The Lagrangian is
L (x
x
x, λ) = kx
x
x− p
p
pk
2
+ λ
kD
D
Dx
x
xk
2
− a
(8)
from the KKT conditions we get
∇L (x
x
x, λ) = 2(x
x
x− p
p
p)+ 2λD
D
D
T
D
D
Dx
x
x = 0, (9)
λ
kD
D
Dx
x
xk
2
− a
= 0, (10)
and the nonnegativity of the Lagrange multiplier λ ≥
0. However, if λ = 0 from (9) it follows that x
x
x = p
p
p,
which is infeasible since the inequality constraint is
not satisfied. Hence λ > 0 and from (10) it results
that the inequality constraint is active, i.e., kD
D
Dx
x
xk
2
= a.
Thus, solving (9) we get eventually
x
x
x =
I
I
I + λD
D
D
T
D
D
D
−1
p
p
p (11)
where I
I
I denotes the identity matrix, and λ is deter-
mined by
kD
D
Dx
x
xk
2
=
D
D
D
I
I
I + λD
D
D
T
D
D
D
−1
p
p
p
2
= a. (12)
Note that in (11) the inverse exists for any λ ≥
0 and when λ = 0 the solution corresponds to not
smoothing. It is interesting that the solution to (11) is
a linear operator acting on p
p
p. Moreover, the Lagrange
multiplier λ plays the role of a parameter controlling
the degree of smoothing applied to p
p
p. In fact, it is pos-
sible to prove that the quadratic variation of the solu-
tion, namely [x
x
x] = kD
D
Dx
x
xk
2
, is a continuous and strictly
decreasing function of λ for λ ∈ [0, +∞) regardless
of p
p
p, provided that it is not a constant vector.
3
This
is equivalent to say that (12), when p
p
p is not a con-
stant vector, establishes a one-to-one correspondence
between a ∈
0, kD
D
Dp
p
pk
2
i
and λ ∈ [0, +∞), with λ = 0
corresponding to a = kD
D
Dp
p
pk
2
and
lim
λ→+∞
[x
x
x] = 0. (13)
A consequence of this is that we do not need to
know in advance the value of a in (7), as smooth-
ing can be performed according to (11) and λ can be
3
If p
p
p is a constant vector [x
x
x] = [p
p
p] = 0 regardless of λ.
ECG P-WAVE SMOOTHING AND DENOISING BY QUADRATIC VARIATION REDUCTION
291

adapted to fulfill some performance criterion. For ex-
ample, considering the SNR gain
4
as a quality index,
λ can be chosen as the one that entails the maximum
gain.
It is important to consider the computational as-
pects related to the smoothing operation, since a ma-
trix inversion is involved in (11). If the size of the
vector p
p
p is large enough computational problems may
arise. Actually this is not an issue for the typical
length of vectors representing P-waves. However,
if the same algorithm is applied to a complete ECG
recording the computational burden, in terms of time
and memory, and the accuracy become serious issues,
even for batch processing.
It is possible to prove that due to the special struc-
ture of the matrix I
I
I + λD
D
D
T
D
D
D, which is tridiagonal,
smoothing in (11) can be performed with complex-
ity O(n), i.e., linear in the size of vector p
p
p (Golub and
Van Loan, 1996). This property is very important and
makes the proposed algorithm suitable also for real-
time applications.
Eventually, it is worthwhile noting that the algo-
rithm we propose is not limited to P-wave smoothing,
but it can be applied in very general situations, when-
ever smoothing and/or denoising are needed. This is
due to the fact that the formulation and the rationale
behind it, i.e., quadratic variation reduction, havegen-
eral validity. In this regard, we successfully applied it
also to EEG tracings denoising.
4 SIMULATION RESULTS
In order to evaluate performance of the proposed al-
gorithm, a noiseless reference model of P-wave is
needed. In this regard, we considered the P-wave
model reported in (Censi et al., 2007), obtained fitting
linear combinations of Gaussian functions to mea-
sured P-waves. Such a model can be reliably used
to represent real P-waves as documented in the cited
reference.
The noiseless reference model considered is re-
ported in Figure 2. It has a duration of 200ms and
its bandwidth essentially does not exceed 100Hz. It
has been sampled at 2048Hz and the corresponding
samples have been collected in a vector denoted by
p
p
p
0
.
The noiseless P-wave reference model p
p
p
0
has been
corrupted by additive noise, denoted by w
w
w, where the
components of w
w
w are i.i.d.
5
zero mean Gaussian ran-
4
This is the ratio between the SNR after and before
smoothing.
5
Independent identically distributed.
dom variables with variance σ
2
w
. Thus, the corre-
sponding noisy P-wave is
p
p
p = p
p
p
0
+w
w
w. (14)
In order to assess performance of the proposed algo-
rithm the following quantities have been considered:
- the signal-to-noise ratio before smoothing
SNR =
kp
p
p
0
k
2
n· σ
2
w
(15)
where n is the size of vector p
p
p
0
;
- the signal-to-noise ratio after smoothing
SNR
s
=
kp
p
p
0
k
2
kx
x
x− p
p
p
0
k
2
(16)
where (x
x
x− p
p
p
0
) is the error vector with respect to
the reference model p
p
p
0
.
In definition (16), we consider as noise affecting the
smoothed vector x
x
x, both the residual Gaussian noise
and the reconstruction error.
Performances are measured in terms of SNR gain,
defined as
G
snr
=
SNR
s
SNR
=
n· σ
2
w
kx
x
x− p
p
p
0
k
2
. (17)
Simulations have been carried out applying smooth-
ing in accordance with (11) and choosing for λ the
value, denoted by λ
opt
, that entails the maximumSNR
gain.
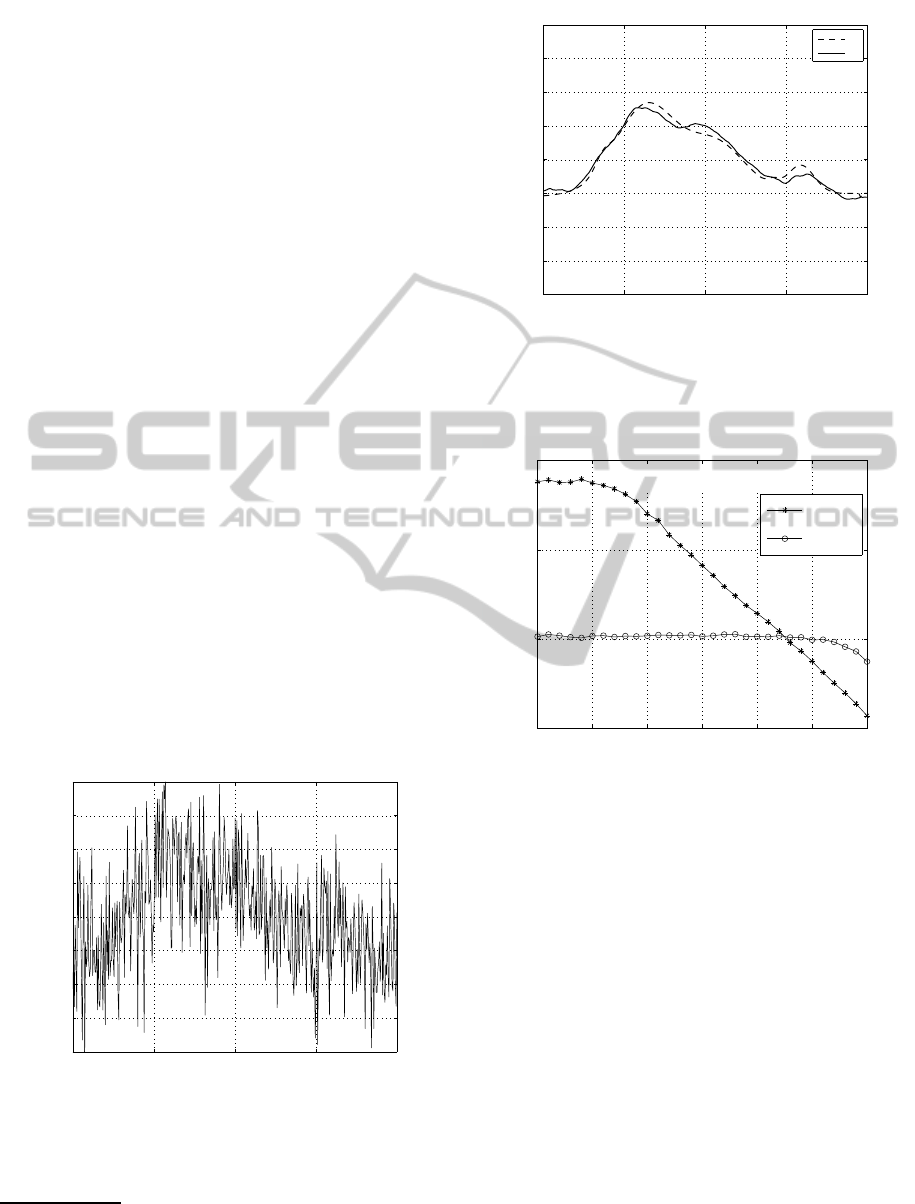
In Figure 2 the noiseless P-wave reference model
p
p
p
0
(dashed-line)is reported. Figure 1 showsthe corre-
sponding noisy version p
p
p, corrupted by additive noise
according to (14), with SNR = 0dB. Note that the
SNR in this case is quite low, nevertheless the pro-
posed algorithm is very effective in denosing p
p
p and
the resulting smoothed vector, namely x
x
x, is plotted
in Figure 2 (continuous-line) for an easy compari-
son with the reference model. In this case the re-
sulting SNR gain is quite remarkable and amounts to
G
snr
= 19.4dB. It is important to point out that we
evaluated the proposed algorithm on different models
of P-wave and the resulting gains were all consistent
with the ones reported in this work.
In order to evaluate how gain varies as input SNR
changes, in Figure 3 we report the average SNR gain
versus input SNR (bottom axis), when the reference
P-wave model of Figure 2 is corrupted by additive
noise with SNR ranging from −20dB to 40dB. The
top axis of Figure 3 represents the corresponding in-
band SNR, computed using the 100Hz bandwidth of
the P-wave reference model. The in-band SNR is
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
292
about
6
10.1dB greater than the corresponding input
SNR.
For each input SNR we considered the solutions
with λ = λ
opt
for 300 noise realizations and then we
averaged the corresponding SNR gains. As Figure 3
highlights, the proposed algorithm exhibits a remark-
able ability in smoothing P-waves. It achieves consid-
erable gains over the whole range of practical input
SNRs and for input SNR ≤ 6dB the average gain ex-
ceeds 15dB. It is remarkable that even when the SNR
is quite high the algorithm exhibits considerable gain.
It is worth noting that the proposed algorithm is
able to reject both out-of-band and in-band noise. In
this regard, low-pass filtering cannot reject in-band
noise without altering the signal. Indeed, an ideal
100Hz low-pass filter, in the same setting of our simu-
lation, would exhibit a constant average gain of about
10.1dB over the whole range of input SNR, as a re-
sult of rejection of the sole out-of-band noise. This
is confirmed by simulation where we considered a
linear-phase FIR low-pass filter synthesized applying
the window method (Oppenheim et al., 1999) to an
ideal 100Hz low-pass filter, using a Kaiser window
and requiring 0.1dB ripple in passband and 80dB at-
tenuation in stopband. In Figure 3 we report the filter
SNR gain versus input SNR, averaged over the same
300 noise realizations used before.
Figure 3 highlights the effectiveness of the pro-
posed algorithm and shows, in particular considering
the in-band SNR, that it outperforms low-pass filter-
ing for all practical values of SNR.
0 50 100 150 200
−0.15
−0.10
−0.05
0
0.05
0.10
0.15
0.20
0.25
Time [ms]
Amplitude [mV]
Figure 1: P-wave reference model of Figure 2 corrupted by
additive Gaussian noise with SNR = 0dB.
6
Actually it is 10log(10.24)dB ≈ 10.1dB, where 10.24
is the ratio between half of the sampling frequency and
bandwidth of the P-wave reference model.
0 50 100 150 200
−0.15
−0.10
−0.05
0
0.05
0.10
0.15
0.20
0.25
Time [ms]
Amplitude [mV]
p
0
x
Figure 2: P-wave reference model p
p
p
0
(dashed-line) and
smoothed solution x
x
x (continuous-line) from the noisy P-
wave of Figure 1.
−20 −10 0 10 20 30 40
5
10
15
20
Input SNR [dB]
Average G
snr
[dB]
Proposed
algorithm
Low−pass
filter
−9.9 0.1 10.1 20.1 30.1 40.1 50.1
In−band SNR [dB]
Figure 3: Average SNR gain G
snr
versus input SNR (bottom
axis) and in-band SNR (top axis).
5 CONCLUSIONS
This work has been motivated by the need to have re-
liable beat-to-beat P-waves, as tracking changes be-
tween consecutive waves turns out to be very impor-
tant in understanding the mechanisms underlying AF.
This is attainable only if noise and artifacts are filtered
out effectively from each single P-wave.
To solve this problem we have developed a
smoothing and denoising algorithm. It is based on
the notion of quadratic variation meant as a suitable
index of variability for vectors or sampled functions.
The algorithm is the closed-form solution to a con-
strained convexoptimization problem, where smooth-
ing and denoising are achieved by reducing the
quadratic variation of noisy P-waves. The compu-
tational complexity of the algorithm is linear in the
ECG P-WAVE SMOOTHING AND DENOISING BY QUADRATIC VARIATION REDUCTION
293

size of the vector to be processed, and this makes it
suitable also for real-time applications. Simulation
results confirm the effectiveness of the approach and
highlight a remarkable ability to smooth and denoise
P-waves.
Eventually, it is worthwhile noting that the pro-
posed algorithm can be effectively applied to a wider
range of signals, e.g., whole ECG or EEG tracings,
whenever smoothing and/or denoising are needed.
REFERENCES
Bayes de Luna, A., Guindo, J., Vinolas, X., Martinez-
Rubio, A., Oter, R., and Bayes-Genis, A. (1999).
Third-degree inter-atrial block and supraventricular
tachyarrhythmias. Europace, 1:43–46.
Benjamin, E. J., Wolf, P. A., D’Agostino, R. B., Silbershatz,
H., Kannel, W. B., and Levy, D. (1998). Impact of
atrial fibrillation on the risk of death: the Framingham
Heart Study. Circulation, 98:946–952.
Boyd, S. and Vandenberghe, L. (2004). Convex Optimiza-
tion. Cambridge University Press.
Carlson, J., Johansson, R., and Olsson, S. B. (2001). Classi-
fication of electrocardiographic P-wave morphology.
IEEE Trans Biomed Eng, 48:401–405.
Censi, F., Calcagnini, G., Ricci, C., Ricci, R. P., Santini,
M., Grammatico, A., and Bartolini, P. (2007). P-
wave morphology assessment by a gaussian functions-
based model in atrial fibrillation patients. IEEE Trans
Biomed Eng, 54:663–672.
Censi, F., Ricci, C., Calcagnini, G., Triventi, M., Ricci,
R. P., Santini, M., and Bartolini, P. (2008). Time-
domain and morphological analysis of the P-wave.
Part I: Technical aspects for automatic quantifica-
tion of P-wave features. Pacing Clin Electrophysiol,
31:874–883.
Clifford, G. D., Azuaje, F., and McSharry, P. (2006). Ad-
vanced Methods And Tools for ECG Data Analysis.
Artech House, Inc., Norwood, MA, USA.
Dilaveris, P. E. and Gialafos, J. E. (2002). Future concepts
in P wave morphological analyses. Card Electrophys-
iol Rev, 6:221–224.
Feinberg, W. M., Blackshear, J. L., Laupacis, A., Kron-
mal, R., and Hart, R. G. (1995). Prevalence, age
distribution, and gender of patients with atrial fibril-
lation. Analysis and implications. Arch. Intern. Med.,
155:469–473.
Go, A. S., Hylek, E. M., Phillips, K. A., Chang, Y., Henault,
L. E., Selby, J. V., and Singer, D. E. (2001). Preva-
lence of diagnosed atrial fibrillation in adults: na-
tional implications for rhythm management and stroke
prevention: the AnTicoagulation and Risk Factors in
Atrial Fibrillation (ATRIA) Study. JAMA, 285:2370–
2375.
Golub, G. H. and Van Loan, C. F. (1996). Matrix compu-
tations. Johns Hopkins University Press, Baltimore,
MD, USA, 3 edition.
Horn, R. A. and Johnson, C. R. (1990). Matrix Analysis.
Cambridge University Press.
McBride, D., Mattenklotz, A. M., Willich, S. N., and
Bruggenjurgen, B. (2008). The Costs of Care in Atrial
Fibrillation and the Effect of Treatment Modalities in
Germany. Value Health.
Nattel, S., Burstein, B., and Dobrev, D. (2008). Atrial re-
modeling and atrial fibrillation: mechanisms and im-
plications. Circ Arrhythm Electrophysiol, 1(1):62–73.
Oppenheim, A. V., Schafer, R. W., and Buck, J. R. (1999).
Discrete-time signal processing (2nd ed.). Prentice-
Hall, Inc.
Perez, M. V., Dewey, F. E., Marcus, R., Ashley, E. A.,
Al-Ahmad, A. A., Wang, P. J., and Froelicher, V. F.
(2009). Electrocardiographic predictors of atrial fib-
rillation. Am. Heart J., 158:622–628.
Platonov, P. G., Carlson, J., Ingemansson, M. P., Roijer,
A., Hansson, A., Chireikin, L. V., and Olsson, S. B.
(2000). Detection of inter-atrial conduction defects
with unfiltered signal-averaged P-wave ECG in pa-
tients with lone atrial fibrillation. Europace, 2:32–41.
Shreve, S. E. (2004). Stochastic Calculus for Finance II:
Continuous-Time Models. Springer Finance. Springer
Science+Business Media, Inc.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
294
