PadeNA: A PARALLEL DE NOVO ASSEMBLER

Gaurav Thareja, Vivek Kumar

Aditi Technologies, Manyata Tech Park, Bangalore, India

Mike Zyskowski, Simon Mercer, Bob Davidson

Microsoft Research, One Microsoft Way, Redmond, WA 98052, U.S.A.

Keywords: DNA Sequence Assembly, Genomics, de Bruijn Graph, Scaffold Generation.

Abstract: Recent technological advances in DNA sequencing technology are resulting in ever-larger quantities of

sequence information being made available to an increasingly broad segment of the scientific and clinical

community. This is in turn driving the need for standard, rapid and easy to use tools for genomic

reconstruction and analysis. As a step towards addressing this challenge, we present PadeNA (Parallel de

Novo Assembler), a parallelized DNA sequence assembler with a graphical user interface. PadeNA is

designed using interface-driven architecture to facilitate code reusability and extensibility, and is provided

as part of the open source Microsoft Biology Foundation. Installers and documentation are available at

http://research.microsoft.com/bio/.

1 INTRODUCTION

Many attempts have been made to address the DNA

sequence assembly problem and all give way to

heuristic methods at some stage. Traditionally,

Sanger sequencing projects have relied on a heuristic

assembly method known as overlap-layout-

consensus, in which overlaps between reads are used

to guide the assembly. This graph-based model has

inspired the development of applications such as the

TIGR (Sutton, 1995), Celera (Myers 2000), Phrap

(Green, 1996), CAP3 (Huang, 1999), Atlas (Havlak,

2003) and ARACHNE (Batzoglou, 2002)

assemblers.

The latest generation of DNA sequencing

technologies is capable of producing far greater

volumes of data, but these tend to be in the form of

short sequence reads. With short reads eliminating

the reliability of read overlaps, the pioneering work

of Pevzner et al. (Pevzner, 2001) on de Bruijn

graphs now forms the basis of many of the current

generation of short-read assemblers. Velvet

(Zerbino, 2008), ALLPATHS (Butler 2008), Euler

SR (Chaisson, 2008) and ABySS (Simpson, 2009)

all have de Bruijn graphs at the heart of their

algorithms.

Many of the currently available short read de novo

assemblers are single-threaded applications

accessible through a command line interface and

designed to run on a single processor or distributed

memory architectures. While sufficient for the

current requirements of genomics, the increasing

availability of cheap DNA sequence is already

revolutionizing the many branches of genomics

research and finding increasingly broad application

in healthcare and non-traditional fields from

environmental studies to law enforcement. This

radically broadened user base will demand tools that

are compatible with the latest sequencing

technologies, are adapted to their specific needs and

are responsive and intuitive. This in turn requires a

code base that can leverage the capabilities of

computer hardware with shared memory

architectures and facilitate rapid application

development and intuitive user interface design.

Many of these needs can be met within a modular

framework of reusable bioinformatics componentry

open to community contribution and freely available

for both commercial and academic developers. Such

a framework would be able to evolve along with the

technologies it supported, extending as needed to

accommodate new experimental techniques and

computer architectures while reducing the level of

196

Thareja G., Kumar V., Zyskowski M., Mercer S. and Davidson B..

PadeNA: A PARALLEL DE NOVO ASSEMBLER.

DOI: 10.5220/0003164301960203

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 196-203

ISBN: 978-989-8425-36-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

effort needed to support an increasingly diverse user

community.

2 IMPLEMENTATION

PadeNA (the Parallel de Novo Assembler) has been

implemented with the principles of code

modularization and reusability in mind, and focuses

on the concept of parallelization in shared memory

architecture. This is the first application of its kind

developed for Windows-based users. The major

improvement in PadeNA is interface driven design

(Pattison, 1999) which promotes reusability and

extensibility of code without affecting its data

handling capabilities. In effect, PadeNA is a

sequence of more basic functions, and developers

can easily customize the default algorithm by

inserting or substituting their own custom classes to

meet the needs of their users. In order to

demonstrate the functionality of PadeNA, we have

also developed a graphical user interface using

Windows Presentation Foundation, providing a

usable and intuitive interface to this and other

assembly algorithms.

PadeNA is built as a part of a .NET based open-

source bioinformatics library, the Microsoft Biology

Foundation (MBF). It uses .NET 4.0 constructs for

multi-core parallelization and performance scales

well on computers with two or more processors as

compared to single-core systems.

Microsoft .NET framework uses a method to

improve the runtime performance of computer

programs. This is known as just-in-time compilation

(JIT), also known as dynamic translation. JIT

compilers represent a hybrid approach, with

translation occurring continuously, as with

interpreters, but with caching of translated code to

minimize performance degradation. It also offers

other advantages over statically compiled code at

development time, such as handling of late-bound

data types and the ability to enforce security

guarantees.

Moreover, Native Image Generator, or simply

NGEN is the Ahead-of-time compilation service of

the .NET Framework. It allows a .NET assembly to

be pre-compiled instead of letting the Common

Language Runtime do a Just-in-time compilation at

runtime (Biswas, 2006).

Further, bioinformatics researchers working in

Unix/Linux environment can take advantage of

Mono 2.8 for extending PadeNA. Mono is an open

source, cross-platform, implementation of C# and

the CLR that is binary compatible with

Microsoft.NET (Mono, 2004).

2.1 Microsoft Biology Foundation

The Microsoft Biology Foundation is an open source

reusable .NET library and application programming

interface for bioinformatics research. Application

developers can use MBF to perform a wide range of

tasks; DNA, RNA and protein sequences can be

imported from files in a variety of standard data

formats, including FASTA, FASTQ, GenBank,

GFF, BED, SAM and BAM. Analysis of these

sequences can be performed using one of several

sequence alignment algorithms including Smith-

Waterman, Needleman-Wunsch, pairwise overlap

aligner, MUMmer and NUCmer (Kurtz, 2004).

These sequences can also be queried against various

databases using BLAST (Altschul, 1997) services,

hosted at different locations and accessible through a

web service interface. File formatters can be used to

write sequences in the desired supported output

format irrespective of the original input format.

Data files are sometimes large enough that hardware

limitations prevent a parser from loading the entire

data set into memory – this may occur when

handling one very large sequence, or a very large

file (or files) containing many smaller sequences.

MBF implements data virtualization by dividing the

data into blocks and providing the data block by

block to the parser as required by the application.

MBF represents sequence data and metadata with

format-independent Sequence and SequenceRange

objects. These objects efficiently store sequence data

in a variety of encoded formats and provide a

flexible and robust way to represent sequences in the

MBF environment.

MBF applications can be implemented in any .NET-

compatible language. Over 70 of these exist, suiting

many different programming styles and levels of

expertise; examples include C#, F#, Visual Basic

and Python.

2.2 Input Parameters

Kmer Length: The choice of kmer length is a

critical task. The search space depends upon kmer

length, with smaller kmer length increase the

number of vertices in the graph. Larger kmer length

reduces the number of ambiguous edges in the graph

but also significantly impact the true overlaps

between kmers. For optimal graph formation, kmer

length should not be less than half the length of the

PadeNA: A PARALLEL DE NOVO ASSEMBLER

197

longest input sequence and cannot be more than the

length of the shortest input sequence.

Dangle Threshold: Maximum length to traverse

from dead ends till point of ambiguity is reached.

This value is dependent on kmer length. (Default:

Kmer length + 1)

Redundant Path Length Threshold: Maximum

length to traverse from point of ambiguity till paths

converge in the graph. (Default: 3 * (Kmer length +

1))

Erosion Threshold: The parameter erodes bases at

the ends of blunt contigs with coverage less than the

specified threshold. (Default: Square root of median

of kmer coverage)

Contig Coverage Threshold:

The parameter

removes low coverage contigs. (Default: Square root

of median of kmer coverage)

Scaffold Redundancy:

The number of mate pair

connections required to connect a pair of contigs.

(Default: 2)

Depth:

This parameter defines the threshold while

performing depth first search on contig overlap

graph. (Default: 10)

3 ASSEMBLY ALGORITHM

Sequence assembly algorithms typically have two

major phases. In the first phase, contigs are extended

until either they cannot be unambiguously extended

further or they reach an end due to lack of read

coverage.

During the second phase, information from paired-

end reads is used to resolve ambiguities and order

and merge contigs to generate scaffolds. We have

used similar steps to those already available in

ABySS (Simpson, 2009), Euler SR (Chaisson,

2008), BAMBUS (Pop, 2004) and the Greedy Path

Merging Algorithm (Huson, 2002). However we

have parallelized many of them, as described later.

3.1 Building the de Bruijn Graph

The sequence reads are first loaded using the data-

virtualized parser of MBF and read sequences with

ambiguous characters are removed prior to

construction of the graph. The remaining sequences

are broken into kmers by defining a window of

length k and moving it along each sequence one base

at a time. The forward and reverse complementary

sequence of a kmer are considered equivalent. We

consider lexicographically larger kmer sequence as

sequence from positive strand.

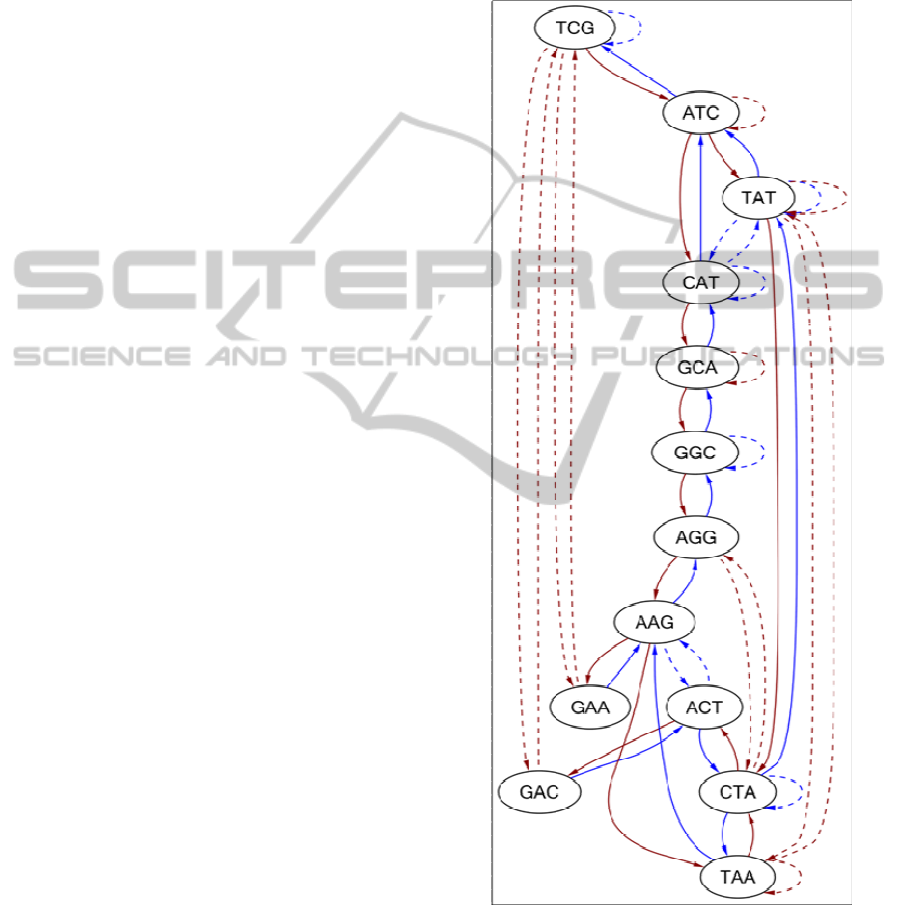
A de Bruijn Graph is a edit distance graph in which

nodes corresponds to objects, and two nodes are

connected if the edit distances between the objects

represented by those nodes is one. Each node in the

Figure 1: Bi-directed de Bruijn Graph for sequence

ATCGACTATAAGGCATCGAA using kmer length = 3.

Where, blue solid lines indicate forward edges, Brown

solid lines indicate backward edges, blue dotted lines

indicate forward edges for reverse complementary

sequence and brown dotted lines indicate backward edges

for reverse complementary sequence.

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

198

graph corresponds to a unique kmer present in some

input sequence or its reverse complement. A

directed edge connects two nodes labeled aα and αb,

where α is a string of length k-1. A bi-directed de

Bruijn Graph is a natural model for the assembly

problem because the two labels for nodes

corresponds two strands of DNA molecule.

3.2 Error Removal

This is the most critical step for assembly. The steps

involved here will remove sequencing errors in the

reads. This process also removes single nucleotide

polymorphisms.

3.2.1 Dangling Link Removal

Any kmer containing a sequencing error is likely to

be unique and will therefore have only a single

connection to a preceding kmer in the graph,

forming a short side branch. The graph is traced for

branches with dead ends and then these branches are

traced back to a point of ambiguity is reached. If the

count of the nodes traversed is less than threshold

value then nodes are removed from the graph. This

step is iteratively performed for bigger branches

with large number of nodes as removal of small

branches may create longer dangling links until the

threshold is reached. The effectiveness of the

dangling link removal step also depends on kmer

length (longer kmers may contain multiple sequence

errors, in turn creating longer dangling links).

3.2.2 Redundant Path Removal

Another common structure found in de Bruijn

graphs is often caused by sequencing errors or single

nucleotide polymorphisms in the middle of reads.

Sequence variation of this kind creates ambiguity in

the graph and impairs contig extension. The graph is

traversed to find all points of divergence, and at each

point of divergence the path is traced forward until a

user-defined threshold is reached. If the paths

converge and contain equal number of nodes, then

the path with lower coverage is removed from the

graph.

3.3 Contig Builder

In the final step of the first phase of sequence

assembly, the graph is traversed to find nodes with

ambiguous edges and these edges are removed,

breaking the graph into a number of sub graphs. The

DNA sequence of each sub-graph is reconstructed

from its constituent kmers to create the initial set of

contigs.

3.4 Scaffold Generation

The second phase takes into consideration mate-pair

information to determine an overall ordering of

contigs.

Libraries of DNA fragments used in sequencing are

frequently generated by experimental techniques that

guarantee all fragments fall within a defined size

range.

Mate-pairs are pairs of reads corresponding to the

DNA sequence at each end of the same fragment of

DNA and have a known strand and orientation

relative to each other. Where the mean and standard

deviation of fragment length is known for a library,

we can estimate the distance between reads in a

mate-pair and use this information to find an order

and orientation of all contigs – a process known as

scaffolding.

Mate pairs from multiple DNA libraries can also be

used in this step. Each library is considered for

distance estimation between contigs.

3.4.1 Aligning Reads to Contigs

Reads are aligned to contigs before attempting to

establish links between contigs. In PadeNA, we

create ungapped alignments by converting each read

to a list of kmers and matching these kmers to a list

of kmers similarly generated from the contig.

3.4.2 Establishing Mate-pair Links

between Contigs

Potential links between contigs are determined from

mate-pair information in the aligned reads. The

information is encoded in the read id, and PadeNA

supports several standard naming conventions.

3.4.3 Filtering Mate-pairs

Mate-pairs are initially filtered based on contig

orientation. The orientation of pair of contigs is the

orientation supported by the largest number of mate-

pairs that connect them. A mate-pair connection is

confirmed between a pair of contigs only if the

number of mate-pairs supporting a particular

orientation is greater than or equal to a threshold

value. This removes spurious links between contigs

and helps in the correct estimation of distance

between contigs. (Pop, 2004)

PadeNA: A PARALLEL DE NOVO ASSEMBLER

199

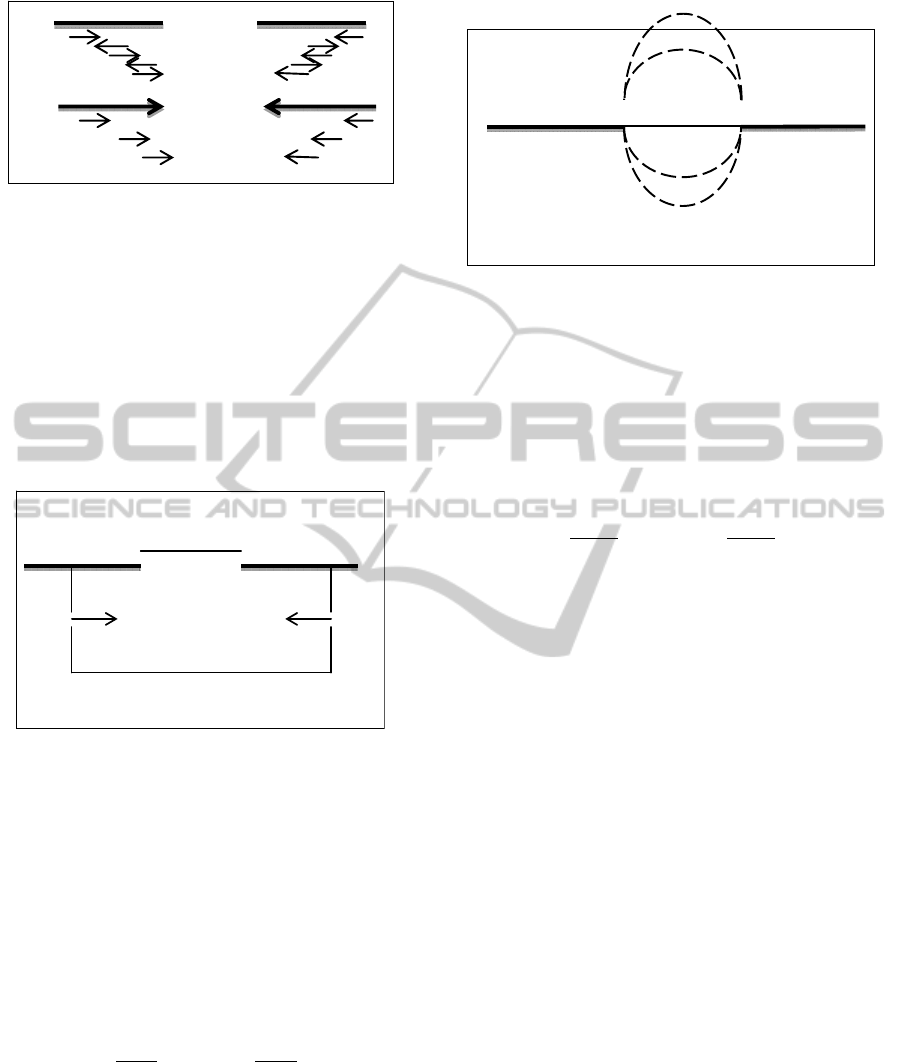
Figure 2: (a) Five mate-pairs are aligned to contig 1 and

contig 2. Out of five mate-pairs, three support forward

contig orientation of contig 1 and two support reverse

orientation. (b) After filtering, the two mate-pairs

supporting reverse orientation for contig 1 are removed

and both contigs are given orientation based on the

majority of mate-pairs.

3.4.4 Distance Calculation

The distance between contigs is calculated using

mate-pair links. Each edge distance is given weight

= 1.

Figure 3: D = m – (l – F(i)) – R(j) where D is the distance

between contigs, m is mean length of fragments in the

library, l is length of contig 1, F(i) and R(j) are respective

positions of alignment between the contig and read.

3.4.4.1 Edge Bundling

If there is more than one-mate pair link between a

pair of contigs, these mate-pairs are bundled into a

single distance provided that mate pair distances lie

in ± 3σ range from the median distance between

contigs. The length of the new edge after bundling is

p/q and standard deviation = 1/ √q where:

=

∑























and =

∑















(1)

This process is repeated until no edges fall in this

range. The weight of the new edge is equal to the

sum of the weights of the bundled edges. (Huson,

2002).

Figure 4: D1, D2, D3, D4 are distances between a pair of

contigs with different mate pairs. D represents distance

between contigs after edge bundling.

3.4.4.2 Weighted Reduction

If there are still edge distances which cannot be

bundled using the above criterion, we perform

weighted bundling, taking the weight of all edges

into account:





∑











∑











and 







∑











∑











(2)

Where l(e) denotes length of the new edge and σ(e)

denotes the standard deviation of the new edge. The

weight of the new edge will be the sum of the

weights of all merged edges.

3.4.5 Contig Overlap Graph

A contig overlap graph is created for a given set of

contigs. Each node represents a contig and contigs

are connected to other contigs if there is k -1

overlap, where k denotes kmer length used for

construction of contigs. (Huson, 2002).

3.4.6 Graph Traversal

The graph is traversed in a depth-first search manner

to look for a single unique path from start contig C

until all contigs paired with C

are included in the

path. As the graph can be extremely dense in

repetitive areas, parameter threshold value is defined

to limit the depth of search in the graph. This

process is repeated for each contig C

The final step

removes overlapping contigs and stitches together

the consistent paths to generate the scaffolds.

(

)

(

)

Contig 1

Contig 2

Mean and standard deviation of library (m, σ)

Distance D

F(i)

R(j)

Distance D

Conti

istance D

Distance D

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

200

4 PARALLELIZATION

IN PADENA

Each step in PadeNA is individually parallelized

which aids in extensibility and reusability of code.

4.1 Parallel de Bruijn Graph

Construction

A de Bruijn Graph is the core data structure used in

the assembly process. In PadeNA, we have

developed a unique implementation of the de Bruijn

Graph for shared memory architecture systems. The

entire read set is portioned using .NET Partitioner

equal to the number of cores in the system. Then

individual core constructs kmer dictionary on

portioned reads. Finally, dictionaries are merged into

a single dictionary. While constructing dictionary

forward and reverse complement are treated as

same. Each kmer sequence as key in dictionary is

defined as a node of a de Bruijn Graph. The

adjacency information of each node is generated

independently. Each node can be connected to a

maximum of 8 neighbors, each sharing a (k -1)

overlap with the node either in the forward or

reverse direction. This connectivity information is

also stored in nodes to fasten the step of graph

traversal.

4.2 Error Removal

Dangling links identification and removal steps are

both performed as a parallelized activity. Redundant

paths which are also present can be similarly

removed in parallel. For definitions of dangling links

and redundant paths, please refer to the assembly

algorithm section.

4.3 Scaffold Generation

Scaffold generation is the second phase of assembly.

As with previous phase of assembly, each step is

individually parallelized.

4.3.1 Contig Overlap Graph

The contig overlap graph is a core data structure for

the second phase of assembly. Each contig is

considered as a node of the graph. Each contig

independently locates its neighbor such that each

neighbor should have a (k-1) overlap in either

forward or reverse complement direction.

4.3.2 Depth-First Search

The contig overlap graph is traversed in a depth-first

fashion to generate all possible paths meeting the

distance constraints imposed by mate-pair data. This

step can be parallelized because each path

originating from different node can be traversed

independently and a list of paths generated. These

paths may then be merged to generate scaffolds.

4.4 Scalability of PadeNA

on different cores

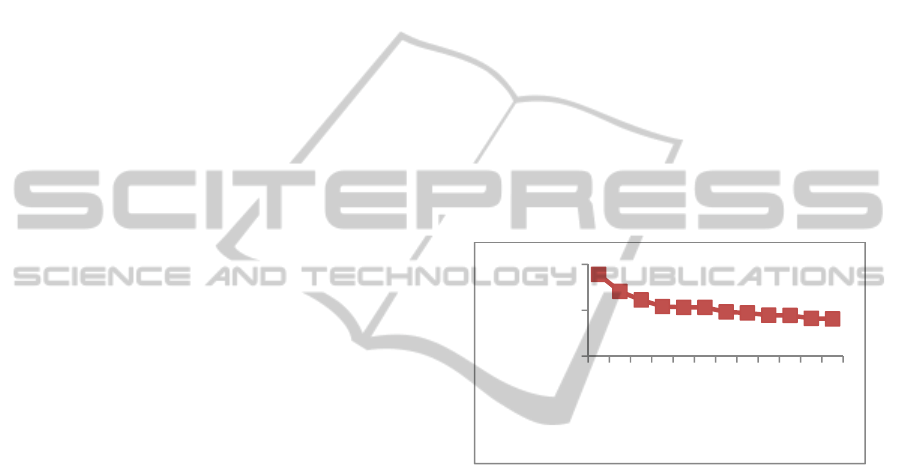
The scalability of the algorithm is a major concern

while parallelization of algorithm. The Euler dataset

as explained in results section is used to assemble

using default parameters on various system

configurations.

The scalability of the algorithm depends on size of

the data and error rate.

Figure 5: Variation of time taken for assembly vs. number

of processors.

5 ASSEMBLY ANALYSIS

For all data sets, only contigs ≥ 100 bp in length

were used for evaluation. In addition, contigs are

only considered to be aligned, if they align ≥ 95% to

a reference genome, if available. The parameters

used to estimate quality of assembly are:

• N50: N50 is a statistical measure given in base

pairs, such that 50% of the assembled genome

lies in contigs of at least this length.

Genomic Coverage: The percentage of bases

of reference genome covered by contigs or

scaffolds. This is computed using the MUMmer

(Kurtz, 2004) tool where a reference genome is

available.

• Largest contig/Mean size of contigs/number

of contigs ≥ 100 bp

These parameters are calculated and used as a

guideline to denote relative quality of the

100

24681012141618202224

Time (in seconds)

Number of Cores

PadeNA: A PARALLEL DE NOVO ASSEMBLER

201

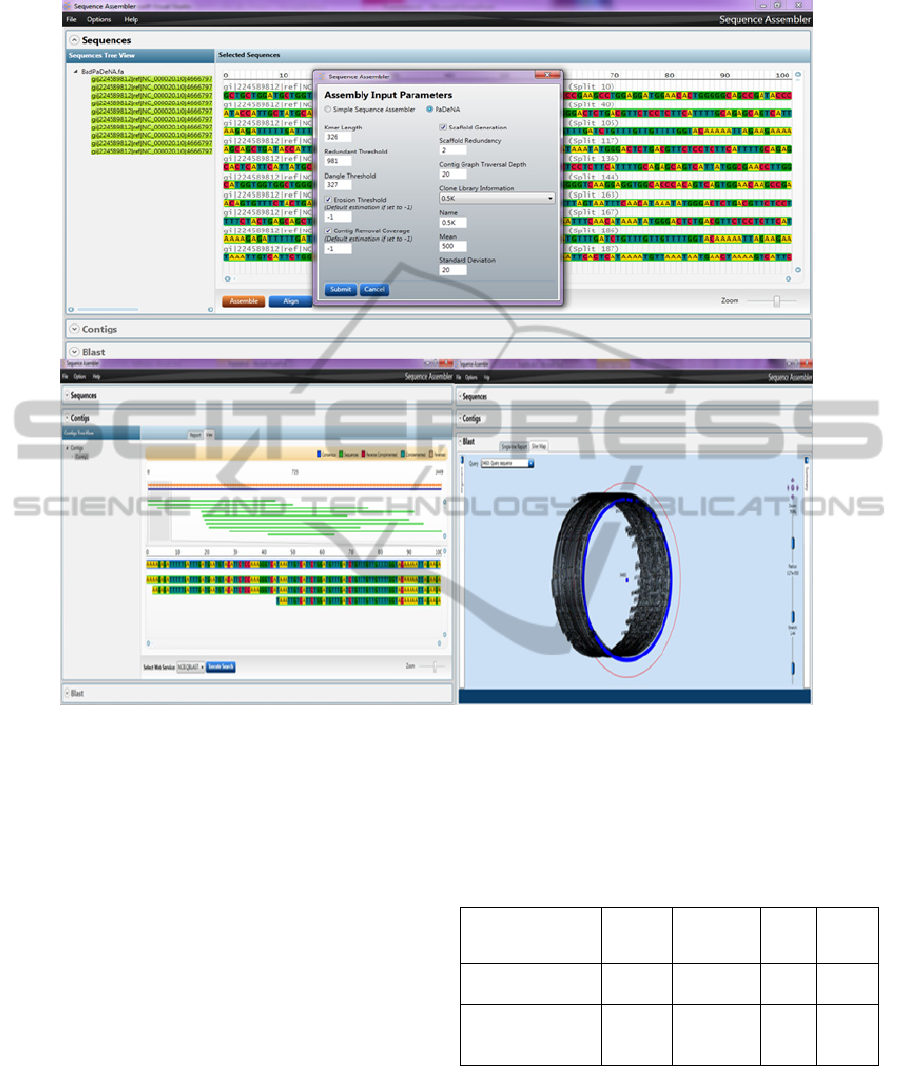
Figure 6: Sequence assembler view of sequence assembly and BLAST result for assembled sequence.

assembly performed (De Novo, 2009). MUMmer is

used for alignment because of its speed and

suitability for genome-level alignments

6 RESULTS

6.1 Evaluation of PadeNA Assembly

using Euler Data

The data used for the analysis is the data provided

by the Euler SR (Chaisson, 2008) tool as test data. It

is a 6.8 MB paired-read dataset with mean insert

length of 1000bp and standard deviation of 500bp.

We performed assemblies with Euler SR. version

1.1.2 and PadeNA version 1.0. Assemblies were

analyzed using the above-mentioned assembly

analysis parameters.

The results show PadeNA produces more

contigs, which may be due to repeats in the base

sequence. The reference sequence was not available

and so we were not able to calculate genomic

coverage and analyze the reason for a large number

of contigs.

Table 1: Comparison of PadeNA output quality against

Euler SR.

Assembler

Contigs

≥ 100 bp

Mean Size

(in bp)

N50

Largest

Contig

(in bp)

Euler SR version

1.1.2 (k = 20)

19 5185 14335 30523

PadeNA

(k = 20 and Depth =

50 10543 30628 30673

7 DISCUSSION

The PadeNA algorithm described above is included

as part of the broader Microsoft Biology Foundation

(MBF) library of general bioinformatics

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

202

functionality, and is available directly to the

application developer or may be accessed by the

user via the included Sequence Assembler

demonstration application (Fig. 6). The Sequence

Assembler application is a GUI-based interface to a

range of MBF functions and uses rich user interface

elements to enable visualization and manipulation of

genomic data. The user can perform assembly,

alignment and multiple sequence alignment of DNA,

RNA and protein sequences, visualizing the output

in a graphical alignment display built using the

Windows Presentation Foundation and Silverlight.

The Sequence Assembler also provides a connector

to various BLAST (Altschul, 1997) web services,

which can be used to characterize an assembled

sequence using public databases.

While our initial results are promising, some work is

needed to further improve the quality and utility of

the assembled output, especially for large size

genomes. Nonetheless, PadeNA can currently be

used for assembling bacterial genomes on shared

memory architectures and each step can be

customized to handle datasets with different

characteristics, or better meet the needs of different

groups of scientific users.

ACKNOWLEDGEMENTS

We would like to thank the Aditi-Microsoft MBF

Engineering team for their continued support to

make this de novo assembler design and technical

implementation deep, robust and of very high

quality. We would also like to thank Steve Jones,

Inanc Birol and other staff at Canada’s Michael

Smith Genome Center for their kind assistance in

understanding the field of genomics. Last but not

least, a very special thanks to Prasanth Koorma for

his constant motivation and encouragement

throughout the project.

REFERENCES

Altschul Stephen F., Madden Thomas L., Schaffer

Alejandro A., Zhang Jinghui, Zhang Zheng, Miller

Webb, & Lipman David J. 1997,’ Gapped BLAST and

PSI-BLAST: a new generation of protein database

search programs’, Nucleic Acids Res. 25:3389-3402.

Batzoglou S., Jaffe D.B., Stanley K., Butler J., Gnerre S.,

Mauceli E., Berger B., Mesirov J. P., & Lander E. S.,

2002, ‘ARACHNE: a whole-genome shotgun

assembler’, Genome Research, 12:177–189.

Biswas Surupa 2006, The Performance Benefits of NGen.,

Viewed July 5

2010, < http://msdn. microsoft.com/

en-us/magazine/cc163610.aspx>

Butler J., MacCallum I., Kleber M., Shlyakhter I. A.,

Belmonte M. K., Lander E. S., Nusbaum C. N., &

Jaffe D. B., 2008, ‘ALLPATHS: De novo assembly of

whole-genome shotgun microreads’, Genome

Research, 18:810–820.

Chaisson M.J. & Pevzner P.A., 2008, ‘Short fragment

assembly of bacterial genomes’, Genome Research,

pages 18:324–330.

De Novo Assembly using Illumina reads – technical note:

Illumina sequencing, 2009, retrieved July 5

2010,

<http://www.illumina .com/Documents/products/tech

notes/technote_denovo_assembly.pdf>

Green P., 1996, ‘Documentation for Phrap. Technical

report’ Genome Center, University of Washington.

Havlak P., Chen R., Durbin K. J., Egan A., & Ren Y.,

2003, ‘The atlas genome assembly system’, Genome

Research, 14:721–731.

Huang X. & Madan A., 1999, ‘CAP3: A whole-genome

assembly program’, Genome Research, 9:868–877.

Huson Daniel H., Reinert Knut, & Myers Eugene W.,

2002, ‘The greedy path-merging algorithm for contig

scaffolding’, Journal of the ACM (JACM) archive,

Volume 49, Issue 5.

Kurtz S., Phillippy A., Delcher A. L., Smoot M.,

Shumway M., Antonescu C., & Salzberg S. L., 2004,

‘Versatile and open software for comparing large

genomes’, Genome Biology.

Mono: Cross platform, open source .NET development

framework, 2004. Viewed July 5

2010, <

http://mono-project.com/Main_Page>

Myers E. W., Sutton G. G., Delcher A. L., & Dew I. M.,

2000, ‘A whole-genome assembly of Drosophila’,

Science, 287(5461):2196–2204.

Pattison Ted 1999, Understanding Interface-based

Programming, Viewed July 5

2010, <

http://msdn.microsoft.com/en-us/library/aa 260635

(VS.60).aspx>

Pevzner P. A., Tang H., & Waterman M. S., 2001, ‘An

eulerian path approach to DNA fragment assembly’,

Proceedings of the National Academy of Sciences,

98(17):9748–9753.

Pop M., Kosack D. S., & Salzberg S. L., 2004,

‘Hierarchical scaffolding with Bambus’, Genome

Research, 14 (1), pp. 149-159.

Simpson J. T., Wong K., Jackman S. D., Schein J. E.,

Jones S. J., & Birol I., 2009, ‘ABySS: A parallel

assembler for short read sequence data’, Genome

Research.

Sutton G. G., White O., Adams M. D., & Kerlavage A. R.,

1995, ‘TIGR assembler: A new tool for assembling

large shotgun sequencing projects’, Genome Science

and Technology, 1:9–19.

Zerbino D. & Birney E., 2008. ‘Velvet: Algorithms for de

novo short read assembly using de Bruijn graphs’,

Genome Research, 18:821–829

PadeNA: A PARALLEL DE NOVO ASSEMBLER

203