
A FRAMEWORK FOR ACOUSTIC CARDIAC SIGNAL
ANALYSIS
P. Carvalho, R. P. Paiva, D. Kumar, J. Ramos, S. Santos and J. Henriques
Department of Informatics Engineering, University of Coimbra, Pólo II, Coimbra, Portugal
Keywords: Non-cardiac Sound Detection, Heart Sound Segmentation, S3 Detection, S2 Split Detection, Heart Murmur,
Systolic Time Intervals.
Abstract: Cardiac auscultation is a traditional, yet highly sensitive and specific diagnosis technique for cardiovascular
diseases. We present a Matlab framework for cardiac signals processing and analysis, which includes a new
toolbox specifically designed for the main processing tasks related to heart sound analysis. Existing
frameworks for acoustic cardiac signal analysis usually limit themselves to noise contamination detection,
S1 and S2 segmentation and murmur diagnosis. Besides these operations, the proposed framework includes
algorithms developed for segmentation of the main heart sound components capable of handling situations
with high-grade murmur, S3 detection and identification, S2 split identification as well as systolic time
intervals (STI) measurement using heart sound. Methods for cardiac function parameter extraction based on
STI are also included. Most of the algorithms outlined in the paper have been extensively evaluated using
data collected from patients with several types of cardiovascular diseases under real-life conditions. The
achieved results suggest that the algorithms developed for the framework exhibit performances that are
comparable and, in most cases, surpass existing state of the art methods.
1 INTRODUCTION
Cardiovascular diseases (CVD) are the leading cause
of death worldwide. According to the European
cardiovascular disease statistics report (Allender, et
al. 2008), 44% of all deaths in men in Europe are
due to CVD, whereas the disease accounts for 54%
of all deaths in women. CVD is not solely a problem
of developed countries, quite the contrary. In fact, as
is mentioned in the WHO report on chronic diseases
(WHO, 2005), 80% of all deaths worldwide due to
chronic diseases occur in middle and low-income
countries, being CVD by far the most prevalent
chronic disease. Recent studies have shown that
premature CVD and its consequences can be largely
prevented and controlled by fostering healthy
lifestyles and by timely detection/control of
progression of the disease. For the population that
already exhibits the disease, the later is of paramount
importance since timely diagnosis usually leads to
more successful and cost effective therapies. Due to
the unprecedented aging of the world population
(Rechel et al., 2009), timely action has decisive
impact on health provision systems’ sustainability.
The first line of defense against CVD is the regular
follow-up by primary care physicians. Given the
medical, social and economical implications of
CVD, a significant research trend is observed in
science and technologies to deploy personal health
(pHealth) systems for CVD management (e.g.
Habetha, 2006). The goal of these systems is to
support physicians and patients in detecting trends
and in collecting data for clinical decision support.
In order to implement cost effective CVD
prevention strategies, pHealth systems as well as
physicians require affordable, comfortable and
highly discriminative information sources for
diagnosis. Traditionally, the electrocardiogram
(ECG) and heart sound (HS) auscultation are among
the most used signals for CVD diagnosis. These
information sources provide complementary
information: the ECG enables to assess the electrical
activity of the heart, while heart sounds provide
information on the mechanical activity of the heart
(Tavel, 1967). Other signals, such as the impedance
cardiogram (ICG) as well as the
photoplethysmogram (PPG), are less common in
daily practice or are still used mainly in research
scenarios.
151
Carvalho P., P. Paiva R., Kumar D., Ramos J., Santos S. and Henriques J..
A FRAMEWORK FOR ACOUSTIC CARDIAC SIGNAL ANALYSIS.
DOI: 10.5220/0003134701510160
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 151-160
ISBN: 978-989-8425-35-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

In this paper we introduce a Matlab framework for
the acquisition and processing of cardiac signals.
The framework (see fig. 1) includes a general real-
time signal acquisition toolbox to interface medical
Figure 1: (top) Layer architecture of the proposed
framework. (bottom) Detailed layer architecture of the
heart sound processing toolbox.
sensor networks and a collection of signal analysis
toolboxes for the most pertinent signals to deploy
portable and non-invasive devices for CVD
diagnosis. Regarding the signal processing layer of
the framework, the focus of this paper will be to
present the algorithms developed by the team for the
HS toolbox. These include methods for noise
detection, heart sound segmentation into its main
components (S1, S2 and S3) as well as higher level
operations such as S2 split detection (important to
assess pulmonary artery pressure), regurgitation and
stenosis murmur detection and classification, and left
ventricle cardiac function assessment (systolic time
intervals, contractility and stroke volume). The
remaining toolboxes are presented elsewhere: a
description of the ECG toolbox can be found in
(Henriques et al., 2008); the ICG algorithms
implemented in the ICG toolbox are described in
(Carvalho et al., 2011), whereas the PPG toolbox is
based on the segmentation method introduced in
(Chan et al., 2007).
Heart sound is a consequence of turbulent blood
flow and vibrating cardiovascular structures, which
propagate to the chest. These vibrations typically
result from myocardial and valvular events that are
affected by the function, the hemodynamics and
electrical activity of the cardiac muscle. The later
have a direct impact on the morphological, spectral
and the timing characteristics of the main heart
sounds (S1, S2 and S3), which have been found to be
highly sensitive and specific for several important
diagnosis tasks ranging from heart valve dysfunction
(Durand & Pibarot 1995), (Abbas&Bassam, 2009) to
systolic cardiac function (Paiva et al. 2009; Tavel
1967).
Unfortunately, cardiac auscultation - the
interpretation of heart sounds - requires highly
proficient physicians. Several studies (e.g. Lam et
al., 2005) have shown that the ability of physicians
to perform cardiac auscultation is reduced and
significantly impaired as time progresses. It is
estimated that this might lead to a number of missed
diagnosis and to a high rate of unnecessary referrals
to cardiologists with a consequence of waste of
scarce resources (Pease, 2001). Hence, the existence
of signal analysis algorithms for HS to deploy
decision support systems, both for the physicians in
their clinical practice as well as to deploy pHealth
systems, are one possible solution to fully explore
this highly informative, low cost and non-invasive
information source on cardiac state.
There are few known integrated frameworks for
heart sound acquisition and processing. Most of the
existing literature is concentrated on algorithms for
elementary processing functions (most of the efforts
focus on HS segmentation and murmur
classification). An extensive review on algorithms
for heart sound analysis as well as CVD diagnosis
algorithms based on HS can be found in
(Abbas&Bassam, 2009; Durand&Pibarot, 1995;
Tavel, 1967). Rajan et al. (1998) introduce an
integrated framework for HS processing based on
Morlet wavelet bank of correlators. Their framework
tackles the problems of noise detection, S1 and S2
segmentation and murmur/click/snap classification.
Javed et al. (2006), describe a signal processing
module that includes a signal acquisition
functionality. Time-frequency processing is wavelet-
based and is limited to HS segmentation and murmur
detection. More recently, Syed et al. (2007)
introduced a framework with similar functionalities
as the one described in (Rajan et al., 1998).
Kudriavtsev et al. (2007) introduce a framework for
HS analysis based on time-frequency signatures
assessed using the Wigner-Ville distribution. This
framework enables HS segmentation, including S3
and S4 detection, as well as murmur detection. It is
observed that none of the sited frameworks include
modules for systolic time interval measurement, i.e.
the pre-ejection period (PEP) and the left ventricle
ejection time (LVET), which is related directly to the
left ventricle function. Some of these frameworks
include facilities to assess the so-called
electromechanical time interval, RS2, defined by the
ECG’s R-peak and the S2 sound; it should be noted
that RS2≈PEP+LVET. However, as was mentioned
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
152
by Oh and Tajik (2003), reduced systolic left
ventricle function will have opposite effects on PEP
and LVET, possibly cancelling each other out.
The paper is organized as follows: Section 2 outlines
the algorithms that have been developed by the team
and are integrated into the heart sound processing
toolbox. In section 3 we present and discuss results
of the main modules that comprise the toolbox.
Finally, in section 4 some main conclusions are
drawn and the main directions for future work are
outlined.
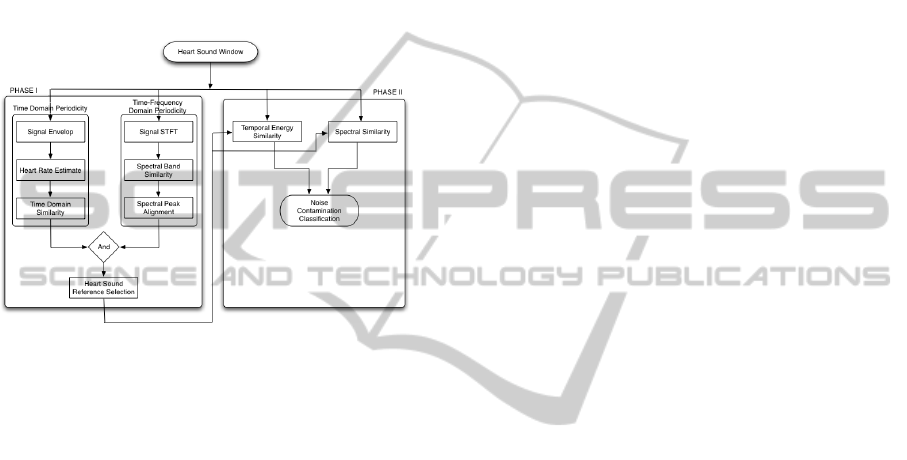
Figure 2: Noise detection algorithm.
2 HEART SOUND ANALYSIS
TOOLBOX
2.1 Noise Detection
The first step in developing a clinical application
based on HS is to exclude signal portions with noise
contaminations. Noise interference in HS might
come from internal (e.g. physiological noises) as
well as external (e.g. noises by bystander) sources
and interfere in highly complex and unpredictable
ways. These noise sources exhibit a very broad range
of spectral bands, loudness and durations. Noise
detection is tackled in the toolbox by observing that
HS are quasi-periodic signals. This characteristic
manifests itself both in the time domain as well as in
the time-frequency domain for different frequency
bands. The proposed strategy is depicted in the
flowchart in fig. 2: in phase I a non-contaminated HS
clip of one complete heart cycle is selected. This HS
will serve as a reference template for further
processing; since this selection operation is always
performed at the start of the signal acquisition
process, it ensures that the method exhibits resilience
towards auscultation site, posture changes and
changing physiological characteristics. In order to
grant that this reference template does not exhibit
noise contamination, the template is selected from
candidates that exhibit the aforementioned quasi-
periodicity characteristics. In the second phase this
template is applied to each signal window using
temporal energy and spectral similarity criteria to
check for noise contamination.
Regarding phase I, first each individual heart
beat is identified in the HS signal. If an ECG is
available, this can be obtained using the R-peaks.
Otherwise, the heart cycle limits can be estimated
from the prominent peaks (which correspond to S1
and S2) of the signal’s envelop and the heart rate
assessed from the singular value decomposition
(SVD) of the envelop of the signal. Let
y
(t) be the
envelop of the HS obtained using the Hilbert
transform. Let
k(wT) = [y(wT), …, y((w+1)T)] and
S(T) = [k
T
(T), …, k
T
(nT)]
T
, nT is limited by the
available duration of y(t). The cardiac beat period T
can be obtained from T = argmax
γ
∈
Ω
(
α
2
/
α
1
)
2
, where
α
1
and
α
2
are the singular values of S(γ) and the
search interval
Ω
is defined using physiological
limits of admissible heart rates. Once each heart
cycle section of the signal’s envelop has been
identified, time domain similarity is checked using
the inner product. Only those cycles which exhibit a
similarity towards its neighbor greater than 0.8 are
retained for further processing. The second test
performed during this phase is performed in the
time-frequency bands. First the spectrogram (0-
600Hz) is split into 15 contiguous, non-overlapping
frequency bands. Since the main energy sources in
HS are due to the S1 and S2 components, it is
observed that the envelops in each time-frequency
band tend to exhibit linear dependent auto-
correlation functions (with decreasing linear
dependency for natural and bioprosthetic valves and
with increasing linear dependency for mechanical
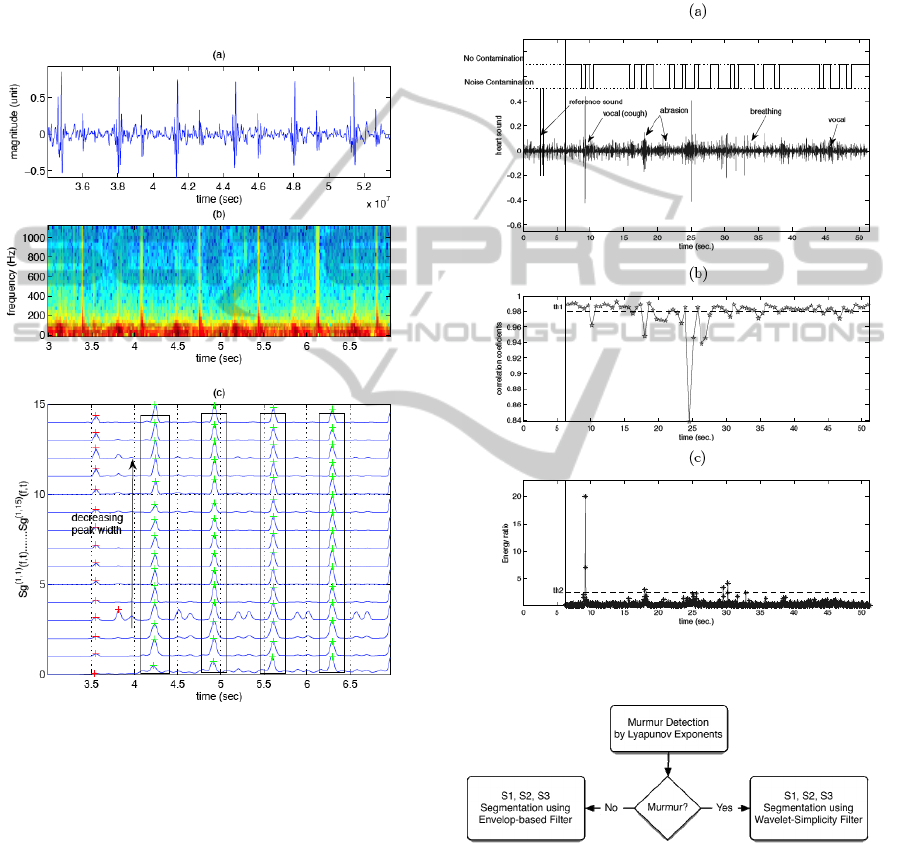
valves) with aligned peaks (see fig. 3). The linear
dependency is assessed using the SVD of the matrix
Λ, whose rows are the autocorrelation functions of
the time-frequency bands. Namely, it is observed
that it has to verify
ρ
1
≥
ρ
2
≥
ρ
3
or
ρ
1
≤
ρ
2
≤
ρ
3
, where
ρ
k
=(
α
k+1
/
α
k
)
2
and
α
k
represents the kth singular value
of
Λ. The heart cycle with the highest average
similarity (radial distance) with respect to all
available heart cycle template candidates is selected
as the template.
Once the reference heart sound has been defined,
phase II is initiated where a template matching
approach is applied to each HS signal window using
the following spectral and temporal features: first the
A FRAMEWORK FOR ACOUSTIC CARDIAC SIGNAL ANALYSIS
153
correlation between spectral power of the template
and the signal under analysis is assessed. If it is
greater than 0.98, then the signal is subject to a
temporal energy test (required to capture very short
duration contaminations). In this test, the energy of
each 50ms signal window is checked against the
energy of the template. The complementary
contributions of these two features in the noise
contamination problem are shown in fig.4.
Figure 3: a) Heart sound from mechanical valve. b)
Spectrogram. c) Auto-correlation functions of the time-
frequency bands.
2.2 Segmentation
HS segmentation into its main constituent parts is
approached using two distinct methods: one is based
on the signal’s envelogram, the other is based on a
wavelet-simplicity filter. The former algorithm is
very efficient computationally. However, its
performance degrades rapidly for HS with murmur.
This type of HS are segmented using a method
developed by the team based on the wavelet-
simplicity filter, which is computationally more
demanding. To automatically select between both
methods, a selection stage has been incorporated into
the segmentation module (see fig. 5).
Heart sounds, particularly those with murmur,
contain nonlinear and non-Gaussian information that
is not tackled by the widely known Fourier or time-
frequency based analysis techniques. Nonlinear
Figure 4: (a) Noise contamination detection results. (b)
Spectral correlation feature. (c) Temporal energy feature.
Figure 5: HS segmentation method.
dynamic techniques not only enable to deal with the
nonlinearity and the non-Gaussianity of a signal, but
also project its dynamic behavior, such as chaos and
complexity, in the state space or the phase space that
is constructed using embedding theory. Based upon
the constructed phase space, the features of a heart
sound signal can be computed. In the proposed
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
154
method, the degree of chaos is measured via the
Lyapunov exponents estimation.
Suppose the heart is considered as a nonlinear
dynamical system X(t + 1) = F[X(t)] that generates
the heart sound time series x(t), t = 1....N . Signal x(t)
can be treated as a one dimensional projection of the
unknown multidimensional dynamic variable X(t).
Phase space transformation of the one dimensional
observation x(t) is performed using the embedding
theorem, attributed to Taken’s theorem, which states
that, using some suitable assumptions, a phase space
can be formed that is topologically equivalent to an
original system (Abarbanel, 1996). The method of
delay is applied to reconstruct the attractor in the
multidimensional space or embedding space P, i.e.
y
i
(t) = [x(t), x(t −
τ
), ....., x(t − (m − 1) τ))]
∈
IR
m
,
where i = 1, 2, 3...P and yi(t) are row vectors of the
embedding matrix Y(t). To determine the exponents
from the embedded matrix Y(t), the nearest neighbor
points are located to measure their distance from the
initial points as given in equation.
λ
=
1
t
M
− t
0
log
2
L
'
t
k
()
L
'
t
k−1
()
k=1
M
∑
where M is the number of repetitions the trajectory
takes in traversing the entire data and denotes the
Lyapunov exponents. For a chaotic dynamical
system it is observed that the Lyapunov exponents
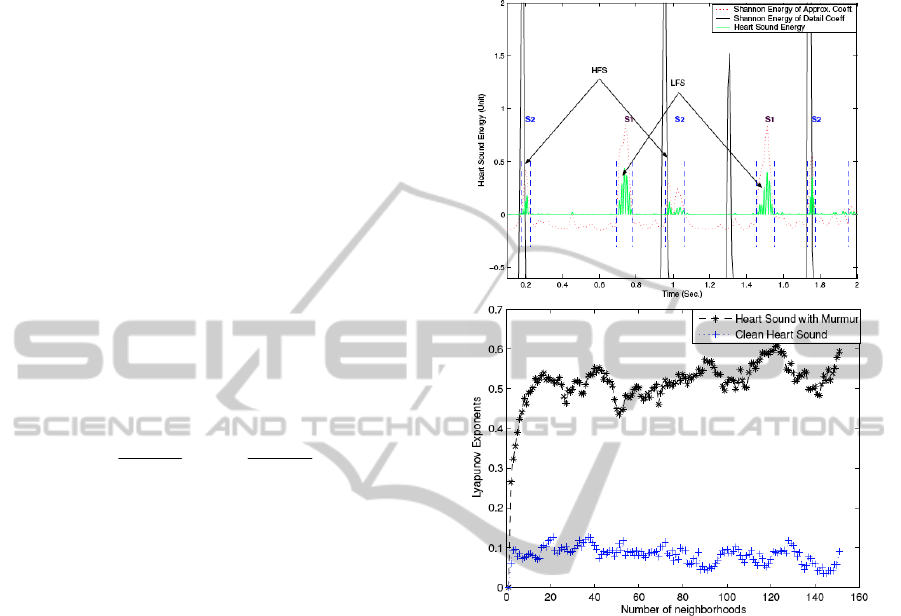
are positive (Abarbanel, 1996). Fig. 6 depicts the
average of 150 exponents obtained from 35 HS clips
(20 clips without murmur and 15 clips with murmur).
As can be observed, HS without murmur are
significantly less chaotic. The decision stage in fig. 5
is implemented using a simple threshold decision
rule.
The segmentation method based on the signal’s
envelop is basically formed by two simple steps
(Kumar et al., 2006a): (i) first the S1 and S2
candidates are identified using the zero-crossings of
the envelop of the approximation coefficients of the
5
th
level wavelet decomposition. The envelop is
computed with a running average of the Shannon
energy. The identification of the S1 and S2
components is based on the observation that pressure
gradients are higher across the aortic valve compared
to the mitral valve. Hence, the S2 heart sound should
exhibit more pronounced high frequency
components compared to S1 or S3. In order to
capture this, a new high frequency feature was
introduced. This new feature is composed by the
Shannon energy of the detail coefficients of the
wavelet transform. As can be seen in fig. 6 (top), this
signature coupled to some simple physiological
motivated rules enable the discrimination between
the different components of the heart sound.
Figure 6: (top) High frequency signature applied to detect
the S2 sounds; HFS and LFS stand for high and low
frequency segment, respectively.. (bottom) Lyapunov
exponents for sound heart sounds with and without
murmur.
Regarding the wavelet-simplicity filter algorithm, it
follows the same steps of the algorithm we
developed using the Wavelet-Simplicity transform
(Kumar et al., 2006). Therefore, only fundamental
changes in the steps of the basic algorithm are
described herein. Murmurs occur between S1 and S2
or S2 and S1 sounds. Therefore, the first task
consists of the identification of the boundaries of the
S1 and S2 sounds. The main steps for achieving S1,
S2 and murmur separation using the strength and
simplicity features are (see fig.7):
Step 1: Heart sound is decomposed using the
wavelet db6. The approximation coefficients are
used in further processing.
Step 2: Simplicity (S
l
) and global strength (GS
l
),
where l is the depth of wavelet decomposition, of the
decomposed signal is computed.
A FRAMEWORK FOR ACOUSTIC CARDIAC SIGNAL ANALYSIS
155
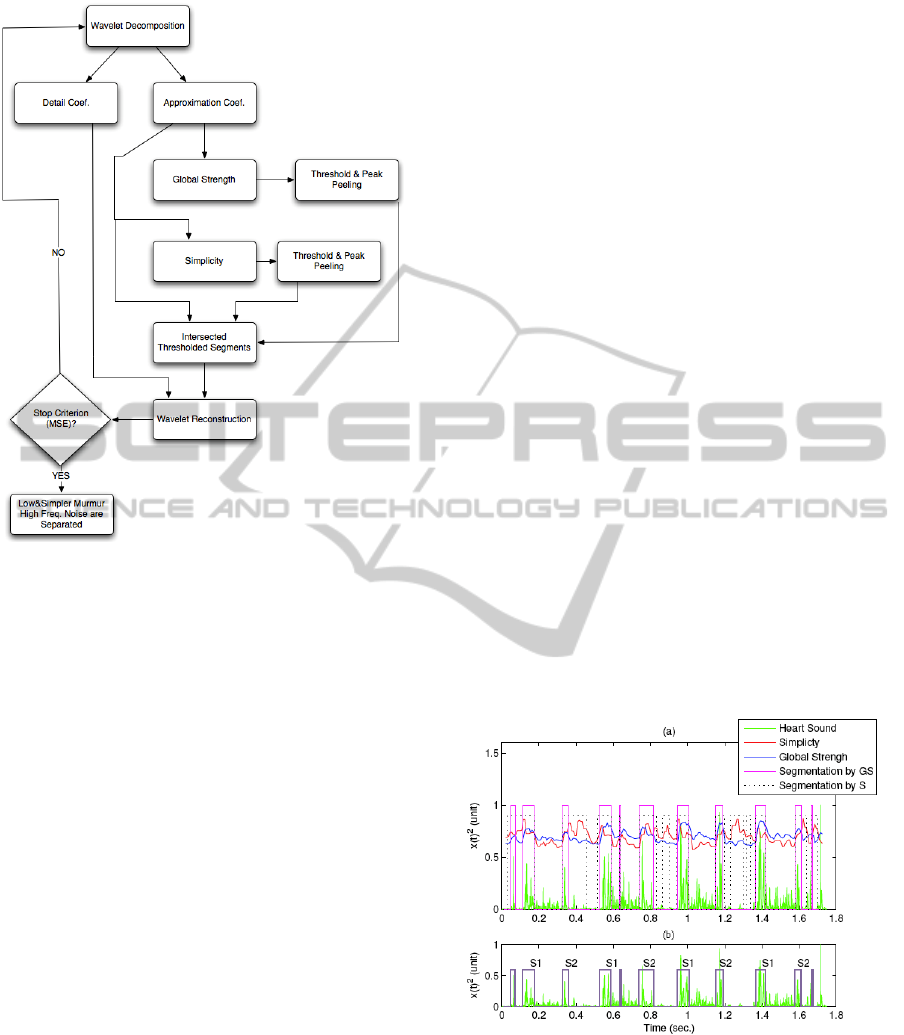
Figure 7: Wavelet-Simplicity Filter segmentation
algorithm.
Step 3: The S1 and S2 components of a heart sound
exhibit high strength and simplicity, hence clear
peaks can be seen in these curves (see fig. 8). In
severe heart murmurs, murmurs overlap S1 or S2
sounds. Other unknown sounds may occur due to
physiological events (e.g. S3) that exhibit similar
characteristics of S1 and S2 components. Usually,
S1 and S2 sounds exhibit relatively high simplicity
as well as strength, whereas other artifacts exhibit
high simplicity but on the contrary low strength.
Therefore, the width (or duration) of S1 and S2
sounds are separately segmented using both feature
curves. For this task, the peak peeling algorithm
(PPA) (Hadjileontiadis and Rekanos, 2003) based
upon an iterative thresholding process is applied.
PPA is applied first to the GS curve and then to the S
curve successively. Subsequently, start and stop
times of S1 and S2 sounds are achieved and can be
gated. The segmented time gates using both feature
curves are shown in fig. 8.
Step 4: It is observed from fig. 8 that correct start
and stop times of S1 and S2 sounds can be achieved
by common segmented time gates in both
thresholded feature curves.
Step 5: The suitable decomposition depth is found
by applying the mean square error criterion on gated
decomposed heart sound signal.
To segment occurrences of the S3 sound, two
additional steps are carried out using physiological
motivated criteria:
1 - Availability of S3 check: two criteria have been
considered to check for the availability of S3 sounds
in a heart sound sample: (i) if the duration of more
than 75% of S2 sounds exceed 250ms. This occurs
when the segmentation algorithm was not able to
separate the S2 and S3 boundaries. (ii) If more than
75% small low complexity segments exhibiting low
duration (50ms-70ms) are detected in the diastolic
phase.
2 – Recognition of S3: S3 are characterized by low
loudness, small duration, low frequency range
(typically between 25-70Hz) and their diastolic
nature, i.e. S3 tend to originate around 150ms after
the onset of the A2 (aortic component of the S2).
Using these properties the following validation
criteria are considered:
-
Loudness: (loudness)
S3
<1/3(loudness)
{S1,S2}
-
Simplicity: due to their lower spectral
content, S3’s simplicity tends to be higher
compared to simplicity of S1 and S2, i.e.
S
S3
>S
{S1,S2}
.
-
The time interval between the onset of S3
and the onset of the preceding S2 is
between 120-180ms.
-
The duration of S3 is between 40-70ms).
Figure 8: Segmentation results in severe (grade V) mitral
regurgitation murmur.
2.3 Murmur Characterization
This module of the toolbox performs murmur
classification using features extracted from the
systolic, i.e. S1-S2, or the diastolic intervals, i.e. S2-
S1. The approach followed is a classical pattern
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
156

recognition approach composed by two layers:
feature extraction and classifier (a SVM with cubic
polynomial kernel function, trained using the one-
against-one binary classification). The classifier
considers seven distinct classes of mrmur: 1) Aortic
Regurgitation (AR), 2) Aortic Stenosis (AS), 3)
Mitral Regurgitation (MR), 4) Pulmonary
Regurgitation (PR), 5) Pulmonary Stenosis (PS), 6)
Subaortic Stenosis+Ventricular Septal Defect
(SAS+VSD), 7) Systolic Ejection (SE). It should be
noted that murmur presence detection is based on
Lyapunov exponents described earlier.
Murmur classification is a challenging task, whose
success is mainly conditioned by the quality of the
features. The features implemented in this toolbox
have been obtained using a feature selection
approach from a pool of 256 features. These features
have been collected using a two-fold approach:
features have been collected from two well-known
methods described in literature and a set of new
features has been introduced (Kumar et al., 2010).
Regarding the feature sets taken from the literature,
the sets introduced by Alhstrom et al. (2006) and by
Olmez and Dokur (2003) have been considered. The
most discriminative features have been selected
using Pudil’s sequential floating point forward
selection method. The module allows for two
alternative sets of features: the first set is composed
by 17 features that have been selected from the
aforementioned 256 feature pool, and the second one
is composed by 10 features selected among a much
smaller pool of features defined by the team. By
default we favor the less complex solution, although
(as will be discussed later) it exhibits a slightly
smaller sensitivity and specificity compared to the
first set. The implemented features in the second
feature set are those listed in table 1. The transition
rate is defined by transition rate = T
asc
/T
desc
, where
Tasc is the transition time taken from the first
minimum of the energy curve to the maximum
energy, and T
dsc
is the time interval from the energy
maximum to the last subsequent minimum energy.
The remaining features are well-known in signal
processing.
Table 1: feature set for murmur classification.
Loudness
Transition Ratio
Fundamental frequency
Spectral power (100-200Hz)
Spectral power (200-300Hz)
Zero crossing rate
Skewness (time domain)
Spectral Shape
Spectral Flux
Max. Lyapunov Exponent
2.4 Cardiac Function Assessment
The assessment of the left ventricle cardiac function
is based on the extraction of the left ventricle systolic
time intervals (STI), i.e. the pre-ejection period
(PEP) and the left ventricule ejection time (LVET).
These are of major diagnostic importance, since it is
this ventricle’s function to insure the blood flow in
the systemic circulation. STI are defined by the
events of the aortic valve. Namely, PEP is defined by
the time interval between R-peak of the ECG and the
opening of the aortic valve, while LVET corresponds
to time span between the closing and the opening
events of this valve. We have shown (Carvalho et
al., 2009) that S1 and S2 can be applied to extract
the aortic valve events from S1 and S2 using
synchronized echocardiography and HS under
resting conditions. It should be mentioned that, the
framework has other methods to extract STI that can
be applied. For instance, when no ECG is available,
the PPG and the HS can be combined to extract the
STI. These might also be estimated using the ICG
signal, if available. A comparative analysis of some
of these methods and principles in STI estimation
can be found in (Carvalho et al., 2010).
The details regarding the algorithm for the detection
of the aortic events using HS were presented in
(Paiva et al., 2009). The method is based on a
Bayesian approach using instantaneous amplitude.
Once the beat-by-beat STI have been extracted, the
toolbox enables the calculation of the following
cardiac function measures:
Corrected STI with Respect to Heart Rate and
Classification:
The implemented correction
algorithms are those described in (Weissler et al.,
1968) and (Warrington et al., 1988). For STI
correction under exercise, the correction steps
described by Mertens et al. (1981) have been
considered in the toolbox. The toolbox presents
diagnosis information regarding if the STI are
pathological or not.
Contractility Index and Classification: The
contractility index PEP/LVET is computed average
runs of 5 beats. Heart Failure diagnosis is
automatically provided based on clinically validated
threshold.
Stroke Volume and Cardiac Output: The beat-to-
beat as well as the average stroke volume and the
cardiac output are calculated using the model
described in (Rietzschel et al., 2001). It should be
mentioned that these parameters are also extracted in
the ICG toolbox of the framework, where the
Bernstein and Kubicek models have been
A FRAMEWORK FOR ACOUSTIC CARDIAC SIGNAL ANALYSIS
157
implemented (see e.g. Wang et al., 1995).
2.8 2.9 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8
50
100
150
200
250
t(s)
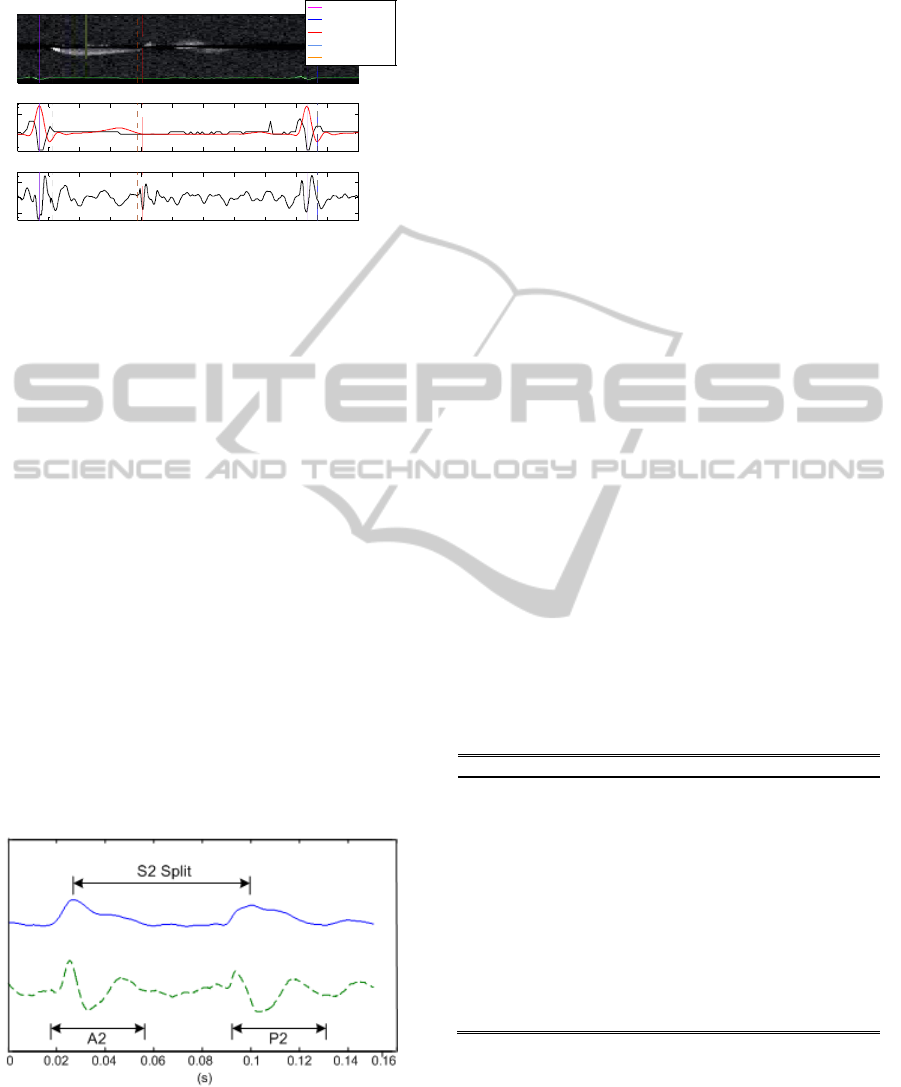
Echocardiography
2.8 2.9 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8
-0.5
0
0.5
t(s)
Electrocardiograms
2.8 2.9 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8
-0.5
0
0.5
t(s)
Phonocardiogram
RPEAKS
AVO from ECHO
AVC from ECHO
AVO from PCG
AVC from PCG
Figure 9: Synchronized echocardiography and heart
sound.
2.5 S2 Split Detection
Pulmonary hypertension (PH) is a serious heart
condition that is difficult to diagnose. Heart sounds
is one of the most relevant diagnosis signal. Usually,
PH leads to wide S2 split between the aortic
component (A2) and the pulmonary component (P2).
Loud P2 is another usual consequence of PH. The
toolbox implements a simple algorithm to assess S2
splitting. The following steps compose the method:
Step 1: S2 frequency range is typically limited to
240Hz. The first step is low-pass filtering using a
Butterworth filter with 240Hz cut-off frequency.
Step 2: The signal’s envelop is extracted using the
Hilbert transform.
Step 3: The two most prominent are extracted. If
their amplitude ratio is greater than a predefined
threshold, then a split is assumed.
Step 4: The split duration is estimated as the time
interval between the two peaks of the signal’s
envelop (see fig. 10).
Figure 10: S2 Split. Upper curve represents the signal’s
envelop. The lower dashed curve is the S2 heart sound.
Time split interval as well as A2 and P2 components are
shown.
3 RESULTS AND DISCUSSION
Table 2 presents the sensitivity and specificity results
of the algorithms implemented in the heart sound
toolbox of the framework. The STI estimation
entries, i.e. PEP, LVET and RS2 entries, refer to the
absolute estimation error with respect to
echocardiography (the clinical gold standard). These
results were obtained using heart sounds acquired at
several hospitals from typical target populations, i.e.
patients suffering from several types of cardio-
vascular diseases such as atrial fibrillation,
tachycardia, premature ventricular contractions,
several types of valve problems with regurgitation
and stenosis, patients with artificial valve implants,
as well as several degrees of heart failure. One
exception to this is the data acquisition protocol
followed to assess the STI measurement algorithms.
In this case, only healthy subjects have been used so
far. The data acquisition study with patients suffering
from heart failure is currently being carried out. It
should also be mentioned that the data collection
study with CVD patients for S2 split assessment is
also ongoing. Regarding the data acquisition for
noise detection, the protocol followed included
contaminations by several distinct internal and
external noise sources at different intensity levels.
All databases have been collected and annotated
under medical supervision. Table 3 summarizes the
population characteristics and the amount of data
collected for each validation database.
Table 2: Summary of results.
Function SE/Abs. Error SP/Corr.
Noise detection 95.88% 97.56%
Segmentation
(without murmur)
97.95% 98.20%
Segmentation
(grade I-IV murmur)
91.09% 95.25%
S2 Split* - -
S3 Identification 90.35% 92.35%
Murmur classification
(set of 10 features)
95.74% 95.01%
Murmur classification
(set of 17 features)
96.15% 96.16%
PEP
7.57±6.17ms
0.52
LVET
11.21±9.27ms
0.88
RS2
9.88±8.65ms
0.92
As can be observed from the results in table 2 and 3,
most of the algorithms developed by team and
integrated into the toolbox have been evaluated
thoroughly. Furthermore, these methods exhibit very
high sensitivity and specificity values. Regarding the
results achieved for STI, the achieved results so far,
suggest that HS enables much better results
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
158

compared to other competing measurement
principles for portable and non-invasive devices (a
detailed analysis can be found in (Carvalho et al.,
2010)). As already mentioned, these results have still
to be confirmed for CVD patients. Regarding the
evaluation of the S3 identification module, it should
be mentioned that currently the algorithm has been
evaluated on sound clips collected from 5 patients.
Hence, the provided results should be considered as
preliminary. As for the S2 split algorithm, evaluation
as been performed only on healthy subjects so far.
Table 3: Validation conditions.
Function N BMI Age
Noise detection 71
25.1±7.8kg/m
2
35.3±12.0y
Segmentation
(without mur.)
55
24.4±1.5kg/m
2
32.6±9.7y
Segmentation
(grade I-IV mur.)
21
24.9±2.3kg/m
2
54.73±6.0y
Murmur classif. 51
25.4±2.2kg/m
2
64.65±8.6y
S2 Split* - - -
S3 Identification 5 NA
15.7±8.7y
STI 33
24.5±2.4kg/m
2
29.7±8.5y
Given the achieved maturity level of the toolbox, it
is being used to deploy clinical applications.
Currently, the team is developing three distinct
applications using the framework: the first
application is called the intelligent stethoscope that
enables the automatic annotation of HS to support
the decision of the physician (for details, the reader
may refer to (Ramos et al., 2011)); the second
application build on top of the first one and is
intended to auscultation training; finally the third and
last application targets prosthetic heart valve implant
dysfunction detection. Applications related to heart
failure management are planned, once the STI
measurement module tests have been concluded.
4 CONCLUSIONS AND FUTURE
WORK
Heart sound is a valuable biosignal to build
diagnosis systems for cardiovascular diseases for the
daily acute clinical practice as well as for systems
dedicated to long-term follow-up of chronic CVD
patients. In this paper we introduce a Matlab toolbox
for acoustic cardiac signal processing. This toolbox
is integrated into a framework for cardiac signal
processing that includes a general real-time signal
acquisition toolbox to interface medical sensor
networks and a collection of signal analysis
toolboxes for the most pertinent signals to deploy
portable and non-invasive devices for CVD
diagnosis. The main algorithms developed
specifically for the heart sound toolbox are outlined.
These include solutions for the main challenges that
are encountered in real life applications based on
heart sounds. In comparison to other existing heart
sound processing frameworks, the proposed toolbox
includes methods for the processing functionalities
that are commonly handled, i.e. noise contamination
detection, heart sound segmentation (including S3
identification) and murmur classification, but also
tackles problems that most known frameworks do
not contemplate. More specifically, methods to
detect S2 splitting and cardiac function assessment
are part of the proposed toolbox. To the best of the
authors’ knowledge, the proposed toolbox is the first
one that enables STI measurement using heart
sounds. This opens new application areas to heart
sounds such as heart failure management.
The proposed framework exhibits a significant
maturity level. Most of the integrated algorithms
have been tested using heart sound clips obtained
under medical supervision and using typical CVD
populations under real-life conditions. The achieved
results are comparable and in most cases exceed the
state of the art in competing methods. It should be
mentioned that the proposed algorithms for STI
measurement and S3 identification have still to be
fully evaluated using a significant database of data
collected from real CVD patients. This is an ongoing
task that will be finished in the near future. It is also
foreseen to continue the research of a more evolved
version of the S2 split detection module. More
specifically, currently the team is researching a
solution to accurately identify the onset of both S2
components, i.e. A2 and P2. This might enable to
correlate the time split to pulmonary artery pressure
measurement as was previously suggested by (Popov
et al., 2004).
ACKNOWLEDGEMENTS
This work was supported in part by SoundForLife
(PTDC/EIA/68620/2006; FCOMP-01-0124-
FEDER-007243) financed by the Portuguese
Foundation for Science and Technology.
REFERENCES
Abarbanel H., 1996, Analysis of observed chaotic data,
Springer- Verlag New York, Inc., 87–90.
A FRAMEWORK FOR ACOUSTIC CARDIAC SIGNAL ANALYSIS
159

Abbas A, Bassam R, 2009, Phonocardiography signal
processing, synthesis lectures on biomedical
Engineering, Morgan and Claypool Publishers.
Ahlstrom C., Hult P., Rask P., Karlsson J., Nylander E.,
Dahlstro U., Ask P., 2003, Feature extraction for
systolic heart murmur classification. Annals of
Biomed. Engg., 34(11):1666–1677.
Allender S., Scarborough P., Petov P., Rayner M., Leal J.,
Luengo-Fernandez R., Gray A., 2008, European
Cardiovascular Disease Statistics 2008, European
Heart Network.
Carvalho P., Paiva R., Couceiro R., Henriques J., Quintal
I., Muehlsteff J., Aubert X., Antunes M., 2009,
Assessing Systolic Time-Intervals from Heart Sound: a
Feasibility Study, IEEE-EMBS.
Carvalho P., Paiva R., Henriques J., Antunes M., Quintal
I., Muehlsteff J., 2011, Robust Characteristic Points
for ICG: Definition and Comparative Analysis,
Biostec: Biosignals. (submitted)
Carvalho P., Paiva R., Henriques J., Quintal I., Muehlsteff
J., Aubert X., Antunes M., 2010, Comparison of
Systolic Time Interval Measurement Modalities for
Portable Devices, IEEE-EMBS.
Chan G., Middleton P., Celler B., Wang L., Lovell N.,
2007, Automatic detection of left ventricular ejection
time from a finger photoplethysmographic pulse
oximetry waveform: comparison with Doppler aortic
measurement, Physiol. Meas. 28:439–452
Durand L. G. and Pibarot P., 1995 Digital signal
processing of the phonocardiogram: review of the
most recent advancements, Crit. Rev. Biomedical
Engineering, 23:163–219
Habetha J., 2006, The MyHeart Project – Fighting
Cardiovascular Diseases by Prevention and Early
Diagnosis, IEEE-EMBS.
Hadjileontiadis L., Rekanos I., 2003, Detection of
explosive lung bowel sounds by means of fractal
dimension, IEEE Signal Proc. Letters, 10(10):311-
314.
Henriques J., Carvalho P., Harris M., Antunes M.,
Couceiro R., Brito M., Schmidt R., 2008, Assessment
of Arrhythmias for Heart Failure Management,
phealth2008 – Int. Workshop on Wearable Micro and
Nanosystems for Personalised Health.
Javed F., Venkatachalam P., Fadzil A., 2006, A Signal
Processing Module for the Analysis of Heart Sounds
and Heart Murmurs, Journal of Physics: Conference
Series; International MEMS Conference, 34:1098–
1105.
Kumar D., Carvalho P., Antunes M., Henriques, J.,
Eugénio L., Schmidt R., Habetha, J., 2006a, Detection
of S1 and S2 Heart Sounds by High Frequency
Signatures, IEEE-EMBS.
Kumar D., Carvalho P., Antunes M., Henriques, J.,
Eugénio L., Schmidt R., Habetha, J., 2006, Wavelet
Transform and Simplicity based Heart Murmur
Segmentation, Computers in Cardiology, 33:173-176.
Kumar D., Carvalho P., Couceiro R., Antunes M., Paiva
R., Henriques J., 2010, Heart Murmur Classification
using Complexity Signatures, Int. Conf on Pattern
Recognition.
Lam M., Lee T., Boey P., Ng W., Hey H., Ho K., Cheong
P., 2005, Factors influencing cardiac auscultation
proficiency in physician trainees, Singapore Med J;
46(1):11.
Mertens H., Mannbach H., Trieb M., Gleichmann U.,
1981, Influence of Heart Rate on Systolic Time
Intervals: Effects of Atrial Pacing versus Dynamic
Exercise, Clin. Cardiol., 4: 22-27.
Oh J., Tajik J., 2003, The return of cardiac time intervals.
The Phonix is rising., J. of the Am. Col. of Cardiology,
42(8):1471-1474.
Olmez T., Dokur Z., 2003, Classification of heart sounds
using ans artifical neural network, Pattern Recognition
Letters, 617-629.
Paiva P., Carvalho P., Aubert X., Muehlsteff J., Henriques
J., Antunes M., 2009, Assessing PEP and LVET from
Heart Sounds: Algorithms and Evaluation, IEEE-
EMBS.
Pease A., 2001, If the heart could speak, Pictures of the
Future, 60–61.
Popov B. Sierra G. Durand L. Xu J., Pibarot P., Agarwal
R., Lanzo V., 2004, Automated extraction of aortic
and pulmonary components of the second heart sound
for the estimation of pulmonary artery pressure, IEEE-
EMBS.
Rajan S., Doraiswami R., Stevenson M., Watrous R.,
1998, Wavelet based bank of correlators approach for
phonocardiogram signal classification, IEEE-SP Int.
Symposium on Time-Frequency and Time-Scale
Analysis , 77 – 80.
Ramos J., P. Carvalho, R. Paiva, L. Vale, J. Henriques,
2011, Intelligent Phonocardiogram Analysis And
Representation Tool, Biostec: HealthInf. (submitted)
Rietzschel E., Boeykens E., Buyzere M. Duprez D.
Clement D., 2001, A comparision between systolic
and diastolic pulse contour analysis in the evaluation
of arterial stiffness, Hypertension, 37:e15-e22.
Syed Z., Leeds D., Curtis D., Nesta F., Levine R., Guttag
J., 2007, A Framework for the Analysis of Acoustical
Cardiac Signals, IEEE Trans. On Biomedical Eng.,
54(4): 651-662.
Tavel M. E., 1967 Clinical Phonocardiography and
External Pulse Recording (Year Book Medical
Publishers, Inc.)
Wang X,, Sun H,, Water J,, 1995, An advanced signal
processing technique for impedance cardiography,
IEEE Trans. On BioMed. Eng., 42(2) 224-30.
Warrington S., Weerasuriya K., Burgess C., 1988,
Correction of systolic time intervals for heart rate: A
comparison of individual with population derived
regression equations, Br. J. Clin. Pharmacol.,
26(2):155-165.
Weissler A., Harris W., Schoenfeld C., 1968, Systolic
Time Intervals in Heart Failure in Man, Circulation,
37; 149-159.
WHO 2005, Preventing Chronic Disease: a Vital
Investment, World Health Organization.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
160
