
INTERACTIVE VISUALIZATION TOOL
FOR TUMOR GROWTH SIMULATIONS
Rafal Wcislo
Department of Computer Science, AGH University of Science and Technology, Cracow, Poland
Keywords:
Simulation, Visualization, Tumor growth, Angiogenesis.
Abstract:
We present the main requirements and ready-to-use components of the interactive visualization tool for mod-
eling of solid tumor proliferation. As the simulation engine it uses complex automata paradigm, which inte-
grates cellular automata with particle dynamics. To make it sufficiently fast for interactive visualization we
show that the system can be efficiently implemented on multicore workstations, with moderate number of pro-
cessors controlled by data parallel interface such as OpenMP. In the near future the system will be empowered
by a combined CPU and GPU computational environment. This in silico lab system is intended for medical
laboratories doing research in oncology and/or in anticancer drug design.
1 INTRODUCTION
There are many mathematical models of tumor
growth driven by the process of angiogenesis (Folk-
man, 1971; Castorina et al., 2009; Bellomo et al.,
2003; Chaplain, 2000; Preziozi, 2003; Mantzaris
et al., 2004; Lowengrub et al., 2010). The models fall
into four categories: (a) continuum models that treat
the endothelial cell (EC) and chemical species den-
sities as continuous variables that evolve according
to a reaction-diffusion system, (b) mechano-chemical
models that incorporate some of the mechanical ef-
fects of EC-ECM (extracellular matrix) interactions
(c) discrete, cellular automata or agent based mod-
els in which cells are treated as units which grow
and divide according to prescribed rules (d) hybrid
multiscale models involving processes from micro-to-
macroscale. Multiscale and multiphysic models rep-
resent the most advanced simulation methodologies.
In (Wcislo et al., 2009) we present the concept of
tumor growth model which is driven by particle dy-
namics (Haile, 1992; Dzwinel et al., 1999; Dzwinel
et al., 2000; Dzwinel et al., 2006; Kadau et al., 2004)
combined with a cellular automata paradigm (Hoek-
stra et al., 2007; Sloot and Kroc, 2009). In this article
we present a tool used for preparation and visualiza-
tion of such a simulation. At a certain stage the cre-
ation of that tool became crucial due to:
• A number of simulation parameters (physical as
well as chemical and biological characteristics of
tissues are defined by as many as a few dozen up
to a few hundred of parameters) which became
very inconvenient to modify manually in the text
file.
• The simulation is expected to consist of several
million of particles (depending on the modeling
there shall be either single cells or their clus-
ters together with the ECM) forming a three-
dimensional fragment consisting of a healthy tis-
sue, an array of blood vessels and a tumor. Thus
a tool that would make it possible to interactively
observe such a simulation would undoubtedly be-
come a significant aid for a researcher.
2 VISUALIZATION TOOL
Figure 1 presents the view of the main screen of the
visualization program.
2.1 Tissue Templates
The simulation program allows several types of tis-
sues to be present simultaneously (a typical situation
in the simulation is when there is a cancerous tissue
surrounded by a healthy one and the two are interwo-
ven with the network of blood vessels). Each tissue
has an array of characteristic features such as density,
an average size of cells, the rate of diffusion of partic-
ular substances (oxygen, TAF), oxygen requirements,
life span, resistance to oxygen deficiency, etc.
270
Wcislo R..
INTERACTIVE VISUALIZATION TOOL FOR TUMOR GROWTH SIMULATIONS.
DOI: 10.5220/0003131402700273
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 270-273
ISBN: 978-989-8425-36-2
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
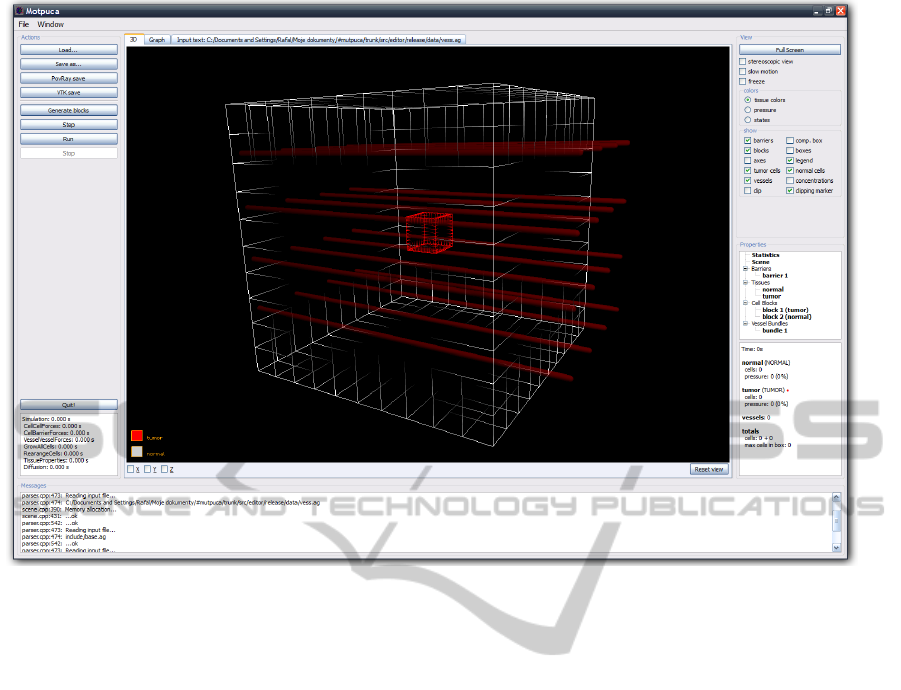
Figure 1: The main window of the visualization program.
The tool has already prepared predefined sets of
data for chosen tissues so it is not necessary to de-
fine all the parameters every time for a certain tis-
sue. These sets are prepared on the grounds of the
biomedical data. During the preparatory stage when
the user of this program deals with the initial values
of the simulation, the data might be easily loaded and,
subsequently, each parameter may be modified. This
modified set of the parameters might also be saved as
a template for other simulations.
2.2 Position, Rotation, Size
Due to the fact that it is impossible to reconstruct
properly a process of blood vessel formation (angio-
genesis) in two dimensions, all the simulations are
currently carried out in three dimensions. 3D makes
the simulation more accurate and consistent with re-
ality; however, it significantly increases the time of
computation and it complicates the way of defining
initial tissue shape and location.
The discussed visualization tool makes it easy to
position the tissues as well as adjust their size, lo-
cation and space orientation so that the creation of
an initial simulation state is facilitated. Such opera-
tions are mostly performed with the help of a com-
puter mouse and a few keyboard shortcuts and func-
tion keys. The program allows the user to watch the
prepared simulation from each side, zoom it, etc.
2.3 Simulation
As soon as the simulation is prepared, the program
makes it possible to run the simulation. It might
be run either on the single-processor computers as
well as on multi-processor ones equipped with a
shared memory (then the simulation program uses the
OpenMP libraries). Due to the parallel execution, the
time of calculation of particular steps is shortened
and, therefore, the simulation is accelerated and the
results are obtained earlier. At present, the research is
being carried out over the implementation of the sim-
ulation on GPU devices.
If the simulation is performed locally, it might be
watched on-line (Fig. 2). In that case the program
shows the information concerning particular tissues
(e.g. the number of cells, the number of cells in vari-
ous states, pressure, O
2
concentration). The program
allows to watch the tissues from any angle as well as
make random cuts so that it is possible to have an in-
sight into a tissue interior.
The visualization program makes optimizations
that allow to watch the simulations - even those con-
sisting of hundreds of thousands of particles - fluently.
INTERACTIVE VISUALIZATION TOOL FOR TUMOR GROWTH SIMULATIONS
271
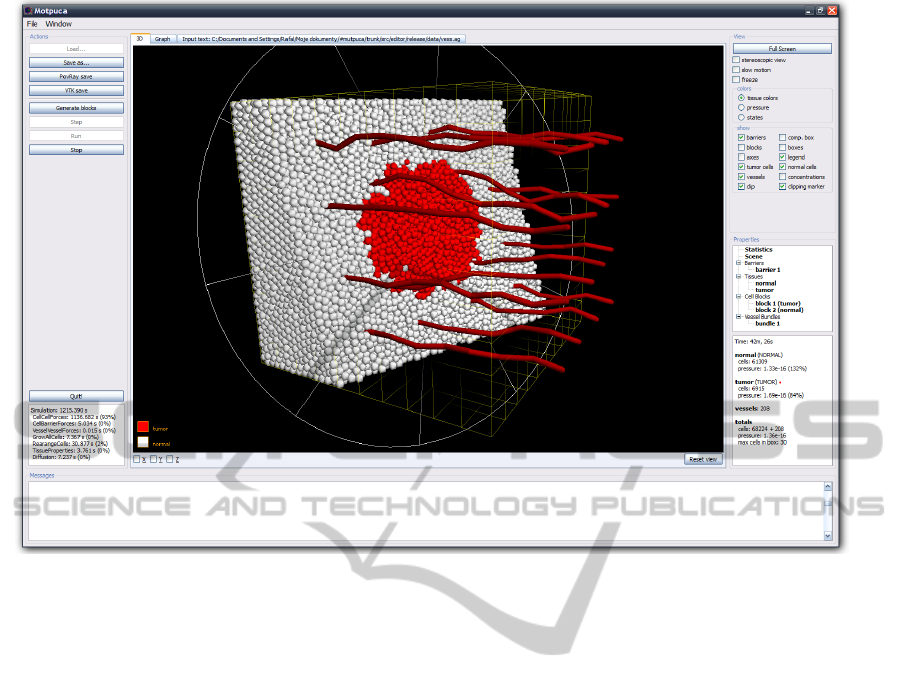
Figure 2: Simulation visualization. Normal cells are marked in white, tumor cells – in red. Tissue section is visible.
It is also possible due to the fact that it has the access
to all the parameters of the simulation. This program,
thus, holds an advantage over other visualization pro-
grams intended for general use.
3 CONCLUSIONS
It should be taken into account that during the creation
of simulation programs, tools that could be used con-
secutively in in silico experiments should also be pre-
pared. It is particularly crucial in the case of prepar-
ing a simulation of complex processes during which it
is necessary to deal with hundreds of parameters and
analyze the results from various dimensions. Such
a convenient and intuitive tool allows to do the re-
search undoubtedly more effectively as well as to ver-
ify one’s hypothesis quicker.
ACKNOWLEDGEMENTS
This research is financed by the Polish Min-
istry of Higher Education and Science, project
N N519 579338 and partially by AGH grant
No. 11.11.120.865.
REFERENCES
Bellomo, N., de Angelis., E., and Preziosi, L. (2003). Mul-
tiscale modeling and mathematical problems related
to tumor evolution and medical therapy. In J Theor
Med., volume 5/2, pages 111–136.
Castorina, P., Carc, D., Guiot, C., and Deisboeck, T.
(2009). Tumor growth instability and its implications
for chemotherapy. In Cancer Res, volume 69 (21).
Chaplain, M. (2000). Mathematical modelling of angiogen-
esis. In J Neuro-Oncol, volume 50, pages 37–51.
Dzwinel, W., Alda, W., Kitowski, J., and Yuen, D. (2000).
Using discrete particles as a natural solver in simulat-
ing multiple-scale phenomena. In Molecular Simula-
tion, volume 20/6, pages 361–384.
Dzwinel, W., Alda, W., and Yuen, D. (1999). Cross-scale
numerical simulations using discrete-particle models.
In Molecular Simulation, volume 22, pages 397–418.
Dzwinel, W., Yuen, D., and Boryczko, K. (2006). Bridg-
ing diverse physical scales with the discrete-particle
paradigm in modeling colloidal dynamics with meso-
scopic features. In Chemical Engineering Sci., vol-
ume 61, pages 2169–2185.
Folkman, J. (1971). Tumor angiogenesis: Therapeutic im-
plications. In N Engl J Med, volume 285, pages 1182–
1186.
Haile, P. (1992). Molecular Dynamics Simulation. Wi-
ley&Sons, New York.
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
272

Hoekstra, A., Lorenz, E., Falcone, L., and Chopard, B.
(2007). Towards a complex automata framework for
multi-scale modeling: Formalism and the scale sepa-
ration map. In Lect Notes Comput Sci, pages 1611–
3349.
Kadau, K., Germann, T., and Lomdahl, P. (2004). Large-
scale molecular-dynamics simulation of 19 billion
particles. In International Journal of Modern Physics,
volume 15(1), pages 193–201.
Lowengrub, J., Frieboes, H., Jin, F., Chuang, Y.-L., Li, X.,
Macklin, P., Wise, S., and Cristini, V. (2010). Non-
linear modelling of cancer: bridging the gap between
cells and tumours. In Nonlinearity, volume 23.
Mantzaris, N., Webb, S., and Othmer, H. (2004). Mathe-
matical modeling of tumor-induced angiogenesis. In
J Math Biol, volume 49/2, pages 1432–1416.
Preziozi, L., editor (2003). Cancer modelling and simula-
tion. Chapman & Hall/CRC Mathematical Biology &
Medicine.
Sloot, P. and Kroc, J. (2009). Complex Systems Modeling
by Cellular Automata, Encyclopedia of Artificial In-
telligence. Informatio SCI, Harshey-Nedw York.
Wcislo, R., Dzwinel, W., Yuen, D., and Dudek, A. (2009).
A new model of tumor progression based on the con-
cept of complex automata driven by particle dynam-
ics. In Journal of Molecular Modeling, volume 15/12,
pages 1517–1539.
INTERACTIVE VISUALIZATION TOOL FOR TUMOR GROWTH SIMULATIONS
273
