
A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK
BOUNDS ON GENERALIZATION OF LEARNING MACHINES
Przemysław Kl˛esk
Department of Methods of Artificial Intelligence and Applied Mathematics, Westpomeranian University of Technology
ul.
˙
Zolnierska 49, Szczecin, Poland
Keywords:
Statistical learning theory, Bounds on generalization, Cross-validation, Empirical risk minimization, Structural
risk minimization, Vapnik–Chervonenkis dimension.
Abstract:
Typically, the n-fold cross-validation is used both to: (1) estimate the generalization properties of a model
of fixed complexity, (2) choose from a family of models of different complexities, the one with the best
complexity, given a data set of certain size. Obviously, it is a time-consuming procedure. A different approach
— the Structural Risk Minimization is based on generalization bounds of learning machines given by Vapnik
(Vapnik, 1995a; Vapnik, 1995b). Roughly speaking, SRM is O(n) times faster than n-fold cross-validation but
less accurate.
We state and prove theorems, which show the probabilistic relationship between the two approaches. In
particular, we show what ε-difference between the two, one may expect without actually performing the cross-
validation. We conclude the paper with results of experiments confronting the probabilistic bounds we derived.
1 INTRODUCTION AND
NOTATION
One part of the Statistical Learning Theory devel-
oped by Vapnik (Vapnik, 1995a; Vapnik, 1995b; Vap-
nik, 2006) is the theory of bounds. It provides prob-
abilistic bounds on generalization of learning ma-
chines. The key mathematical tools applied to derive
the bounds in their additive versions are Chernoff and
Hoeffding inequalities
1
(Vapnik, 1995b; Cherkassky
and Mulier, 1998; Hellman and Raviv, 1970; Schmidt
et al., 1995).
We use this theory to show a probabilistic rela-
tionship between two approaches for complexity se-
lection: n-fold cross-validation (popular among prac-
tioner modelers) and Structural Risk Minimization
proposed by Vapnik (rarely met in practice) (Shawe-
Taylor et al., 1996; Devroye et al., 1996; Anthony
and Shawe-Taylor, 1993; Krzy
˙
zak et al., 2000). We
1
Chernoff inequality: P
|ν
I
− p| ≥ ε
≤ 2 exp(−2ε
2
I),
Hoeffding inequality: P
|X
I
−EX| ≥ ε
≤ 2exp(−
2ε
2
I
B
2
−A
2
).
Meaning (respectively): observed frequencies on a sample
of size I converge to the true probability as I grows large;
analogically: means of a random variable (bounded by A
and B) converge to the expected value. It is a in-probability-
convergence and its rate is exponential.
remind that SRM is O(n) times faster than n-fold
cross-validation (since SRM does not perform any
repetitions/folds per single fixed complexity, nor test-
ing) but less accurate, since the selection of optimal
complexity is based on the guaranteed generaliza-
tion risk. The bound for the guaranteed risk is ex-
pressed in terms of Vapnik-Chervonenkis dimension,
and is a pessimistic overestimation of the growth func-
tion, which in turn is overestimation of the unknown
Vapnik-Chervonenkis entropy. We formally remind
these notions later in the paper. All those overesti-
mations contribute (unfortunately) to the fact that for
a fixed sample size, SRM usually underestimates the
optimal complexity and chooses too simple model.
Results presented in this paper may be regarded
as conceptually akin to results by Holden (Holden,
1996a; Holden, 1996b), where error bounds on
cross-validation and so-called sanity-check bounds
are derived. The sanity-check bound is a proof,
for large class of learning algorithms, that the er-
ror of the leave-one-out estimate is not much worse
— O(
p
h/I) — than the worst-case behavior of the
training error estimate, where h stands for Vapnik-
Chervonenkis dimension of given set of functions and
I stands for the sample size. The name sanity-check
refers to the fact that although we believe that under
many circumstances, the leave-one-out estimate will
5
Kl˛esk P..
A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF LEARNING MACHINES.
DOI: 10.5220/0003121000050017
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 5-17
ISBN: 978-989-8425-40-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

perform better than the training error (and thus jus-
tify its computational expense) the goal of the sanity-
check bound is to simply prove that it is not much
worse than the training error (Kearns and Ron, 1999).
These results were further generalized by Kearns
(Kearns and Ron, 1999; Kearns, 1995a; Kearns,
1995b) using the notion of (β
1
,β
2
)-error stability
2
rather than (β
1
,β
2
)-hypothesis stability
3
imposed on
the learning algorithm.
For the sake of comparison and to set up the per-
spective for further reading of this paper, we highlight
some differences of meaning of our results and the re-
sults mentioned above:
- we do not focus on how well the measured cross-
validation result estimates the generalization error
or how far it is from the training error in the leave-
one-out case — sanity-check bounds (Holden,
1996b; Kearns and Ron, 1999); instead, we want
to make statements about the cross-validation re-
sult without actually measuring it, thus, remaining
in the setting of the SRM framework.
- in particular we want to state probabilistically
what ε-difference one can expect between the
known Vapnik bound and the unknown cross-
validation result for given conditions of the exper-
iment,
- in the consequence, we want to be able to cal-
culate the necessary size of the training sample,
so that the ε is sufficiently small, and so that
the optimal complexity indicated via SRM is ac-
ceptable in the sense that cross-validation, if per-
formed, would probably indicate the same com-
plexity; this statement may seem related to the
notion of sample complexity considered e.g. by
Bartlett (Bartlett et al., 1997; Bartlett, 1997) or Ng
(Ng, 2004), but we do not find the sample size re-
quired for the algorithm to learn/generalize “well”
but rather such a sample size so that complexity
selection via SRM gives similar results to com-
plexity selection via cross-validation,
- we do not explicitly introduce the notion of er-
ror stability for the learning algorithm, but this
2
We say that a learning algorithm has a (β
1
,β
2
)-error
stability, if generalization errors for two models provided by
this algorithm using respectively a training sample of size I
and a sample with size lowered to I −1 are β
1
-close to each
other with probability at least 1−β
2
. Obviously the smaller
both β
1
,β
2
are the more stable the algorithm.
3
We say that a learning algorithm has a (β
1
,β
2
)-
hypothesis stability, if the two models provided by this al-
gorithm using respectively a training sample of size I and
sample with size lowered to I −1 are β
1
-close to each other
with probability at least 1 −β
2
, where closeness of models
is measured by some functional metrics, e.g. L
1
, L
2
, etc.
kind of stability is implicitly derived be means of
Chernoff-Hoeffding-like inequalities we write.
- we do not focus on the leave-one-out cross-
validation; we consider a more general n-fold non-
stratified cross-validation (also: more convenient
for our purposes); the leave-one-out case can be
read out from our results as a special case.
1.1 Notation Related to Statistical
Learning Theory
We keep the notation similar to Vapnik’s (Vapnik,
1995b; Vapnik, 1995a).
• We denote the finite set of samples as:
(x
1
,y
1
),(x
2
,y
2
),.. .,(x
I
,y
I
)
,
or more shortly by encapsulating pairs as
{z
1
,z
2
,.. .,z
I
},
where x
i
∈ R
d
are input points, y
i
are output val-
ues corresponding to them, and I is the set size. y
i
differ depending on the learning task: for classi-
fication (pattern-recognition) y
i
∈{1, 2,..., K} —
finite discrete set, for regression estimation y
i
∈R.
• We denote the set of approximating functions
(models) in the sense of both classification or re-
gression estimation as:
{f (x,ω)}
ω∈Ω
,
where Ω is the domain of parameters of this set of
functions, so a fixed ω can be regarded as an index
of a specific function in the set.
• The risk functional R : {f (x, ω)}
ω∈Ω
→ R ∪
{+∞} is defined as
R(ω) =
Z
x∈X
Z
y∈Y
L
f (x, ω),y
p(x,y)
|{z}
p(x)p(y|x)
dydx,
(1)
where p(x) is the distribution density of in-
put points, p(y|x) is the conditional density of
system/phenomenon outputs y given a fixed x.
p(x,y) = p(x)p(y|x) is the joint distribution den-
sity for pairs (x,y). In practice, p(x,y) is un-
known but fixed, and hence we assume the sample
{z
1
,z
2
,.. .,z
I
} to be i.i.d.
4
L is the so called loss
function which measures the discrepancy between
the output y and the model f . For classification, L
is an indicator function:
L
f (x, ω),y
=
(
0, for y = f (x,ω);
1, for y 6= f (x,ω),
(2)
4
Independent, identically distributed.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
6

and the risk functional becomes R(ω) =
R
x∈X
∑
y∈Y
L
f (x, ω),y
p(x,y)dx. For regression
estimation, L is usually chosen as the distance in
L
2
metric:
L
f (x, ω),y
=
f (x, ω) −y
2
, (3)
and the risk functional becomes R(ω) =
R
x∈X
R
y∈Y
f (x, ω) −y
2
p(x,y)dydx.
• By ω
0
we denote the index of the best function
f (x, ω
0
) in the set, such that:
R(ω
0
) = inf
ω∈Ω
R(ω). (4)
• Since only a finite set of samples {z
1
,.. .,z
I
} is
at disposal, we cannot count on actually finding
the best function f (x,ω
0
). In fact, we look for its
estimate with respect to the finite set of samples.
We define the empirical risk:
R
emp
(ω) =
1
I
I
∑
i=1
L(y
i
, f (x
i
,ω)), (5)
and by ω
I
we denote the index of the function
f (x, ω
I
) such that:
R
emp
(ω
I
) = inf
ω∈Ω
R
emp
(ω) (6)
— Empirical Risk Minimization principle (Vap-
nik, 1995a; Vapnik, 1995b; Vapnik and Chervo-
nenkis, 1989; Cherkassky and Mulier, 1998).
• For simplification of notation and further consid-
erations, we introduce replacements:
(x,y) = z,
L
f (x, ω),y
= Q
z,ω).
In other words instead of considering the set
of approximating functions
5
{f (x,ω)}
ω∈Ω
, we
equivalently consider the set of error functions
{Q(z,ω)}
ω∈Ω
. It is a 1:1 correspondence
6
. Now,
we write the true risk as:
R(ω) =
Z
z∈X×Y
Q(z,ω) p(z)
|{z}
p(x,y)
dz
=
Z
Z
Q(z,ω)dF(z), (7)
and the empirical risk as
R
emp
(ω) =
1
I
I
∑
i=1
Q(z
i
,ω)), (8)
5
In the sense of all learning tasks.
6
Q is identical with L in the sense of their values. They
differ only in formal posing of their domains. L works on
f (x,ω) and y and maps them to error values, whereas Q
works directly on z and ω and maps them to error values.
1.2 Notation Related to
Cross-validation
In the paper, we shall consider the non-stratified vari-
ant of the n-fold cross-validation procedure (Kohavi,
1995). In each single fold (iteration) we first permute
the data set and then we split it at the same fixed point
into two disjoint subsets — a training set and a testing
set. Thus, we guarantee the randomness by permuta-
tion per each fold, and among folds we do not care to
make training sets disjoint pairwise. Since permuta-
tions are independent, hence folds are independent as
well.
Such an approach is somewhere in-between the
classical n-fold cross-validation and the bootstrap-
ping (Efron and Tibshirani, 1993). In the classical
cross-validation, all
n
2
pairs of training sets are mu-
tually disjoint (and so are testing sets) and hence folds
are dependent, whereas in the bootstrapping instead
of repeatedly analyzing subsets of data set, one re-
peatedly analyzes the subsamples (with replacement)
of the data. For more information see (Hjorth, 1994;
Weiss and Kulikowski, 1991; Fu et al., 2005).
We introduce the following notation. I
0
and I
00
stand for the size of training and testing sets respec-
tively.
I
0
=
n −1
n
I,
I
00
=
1
n
I.
Without loss of generality for theorems and proofs, let
I be dividable by n, so that I
0
and I
00
are integers.
In a single fold, let
{z
0
1
,z
0
2
,.. .,z
0
I
0
}, {z
00
1
,z
00
2
,.. .,z
00
I
00
}
represent respectively the training set and the testing
set, taken as a split of the whole permuted data set
{z
1
,z
2
,.. ., z
I
}. Similarly, empirical risks calculated
as follows:
R
0
emp
(ω) =
1
I
0
I
0
∑
i=1
Q(z
0
i
,ω), (9)
R
00
emp
(ω) =
1
I
00
I
00
∑
i=1
Q(z
00
i
,ω), (10)
represent respectively the training error and the test-
ing error, calculated for any function ω.
By ω
I
0
we define the function that minimizes the
empirical training risk
R
0
emp
(ω
I
0
) = inf
ω∈Ω
R
0
emp
(ω) (11)
when the context of discussion is constrained to single
fold. When, we will need to broaden the context onto
A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF
LEARNING MACHINES
7

all folds, k = 1,2,.. .,n, we will write ω
I
0
,k
to denote
the function that minimizes the empirical training risk
in the k-th fold. Therefore, the final cross-validation
result — an estimate of generalization error — is the
mean from empirical testing risks R
00
emp
using func-
tions ω
I
0
,k
:
C =
1
n
n
∑
k=1
R
00
emp
(ω
I
0
,k
). (12)
The independence of folds can be formally ex-
pressed in the following way. For any two indices
of folds k 6= l and for any numbers A,B:
P(R
00
emp
(ω
I
0
,k
) = A, R
00
emp
(ω
I
0
,l
) = B)
= P(R
00
emp
(ω
I
0
,k
) = A) ·P(R
00
emp
(ω
I
0
,l
) = B).
We stress the independence once again, because later
on we are going to sum up several independent proba-
bilistic inequalities into one inequality, and we would
like the result to be true with the effective probability
being the product of component probabilities.
2 THE RELATIONSHIP FOR A
FINITE SET OF
APPROXIMATING FUNCTIONS
2.1 Classification Learning Task
Similarly to Vapnik, let us start with the classification
learning task and the simplest case of a finite set of N
indicator functions: {Q(z, ω
j
)}
ω
j
∈Ω
, j = 1,2,.. .,N.
Not to complicate things, we will keep on writing ω
I
in the sense of the optimal function minimizing the
empirical risk on our finite sample of size I, instead
of writing more formally e.g. ω
j(I)
7
.
Vapnik shows (Vapnik, 1995a; Vapnik, 1995b)
that with probability at least 1 − η, the following
bound on the true risk is satisfied:
Z
Z
Q(z,ω
I
)dF(z)
| {z }
R(ω
I
)
≤
1
I
I
∑
i=1
Q(z
i
,ω
I
)
| {z }
R
emp
(ω
I
)
+
r
lnN −ln η
2I
.
(13)
The argument is the following:
P
sup
1≤j≤N
R(ω
j
) −R
emp
(ω
j
) ≥ ε
≤
N
∑
j=1
P
R(ω
j
)−R
emp
(ω
j
) ≥ε
≤N ·exp(−2ε
2
I).
7
In the sense that j(I) ∈ {1, .. ., N} returns the index of
the minimizer given our data set of size I.
The last pass is true, since for each term in the sum
Chernoff inequality is satisfied. By substituting the
right-hand-side with small probability η and solving
for ε, one obtains the bound:
R(ω
j
) −R
emp
(ω
j
) ≤
r
lnN −ln η
2I
,
which holds true with probability at least 1 −η simul-
taneously for all functions in the set, since it holds for
the worst. Hence, in particular it holds true for the
function ω
I
. And one gets the bound (13).
For the theorems to follow, we denote the right-
hand-side in the Vapnik bound by V = R
emp
(ω
I
) +
p
(lnN −lnη)/(2I).
Theorem 1. Let {Q(z,ω
j
)}
ω
j
∈Ω
, j = 1,2,. ..,N, be
a finite set of indicator functions (classification task)
of size N. Then, for any η > 0, arbitrarily small, there
is a small number
α(η,n) = η −
n
∑
k=1
n
k
(−1)
k
(2η)
k
, (14)
and the number
ε(η,I,N,n) =
2
r
n
n −1
+ 1
!
r
lnN −ln η
2I
+
√
n +
r
n
n −1
r
−lnη
2I
, (15)
such that:
P
|V −C| ≤ ε(η,I,N,n)
!
≥ 1 −α(η, n). (16)
Before we prove theorem 1, the following two re-
marks should be clear.
Remark 1. The value of α(η, n) is monotonous with
η. I.e. the smaller η we choose, the smaller α(η,n)
becomes as well. Therefore the minimum probability
measure 1 −α(η, n) is suitably large.
lim
η→0
+
η −
n
∑
k=1
n
k
(−1)
k
(2η)
k
!
= lim
η→0
+
η + 1 −
n
∑
k=0
n
k
(−1)
k
(2η)
k
!
= lim
η→0
+
η + 1 −(1 −2η)
n
| {z }
→1
= 0.
Remark 2. For the fixed values of η, N, n, the value
of ε(η,I,N,n) converges to zero as the sample size I
grows large.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
8
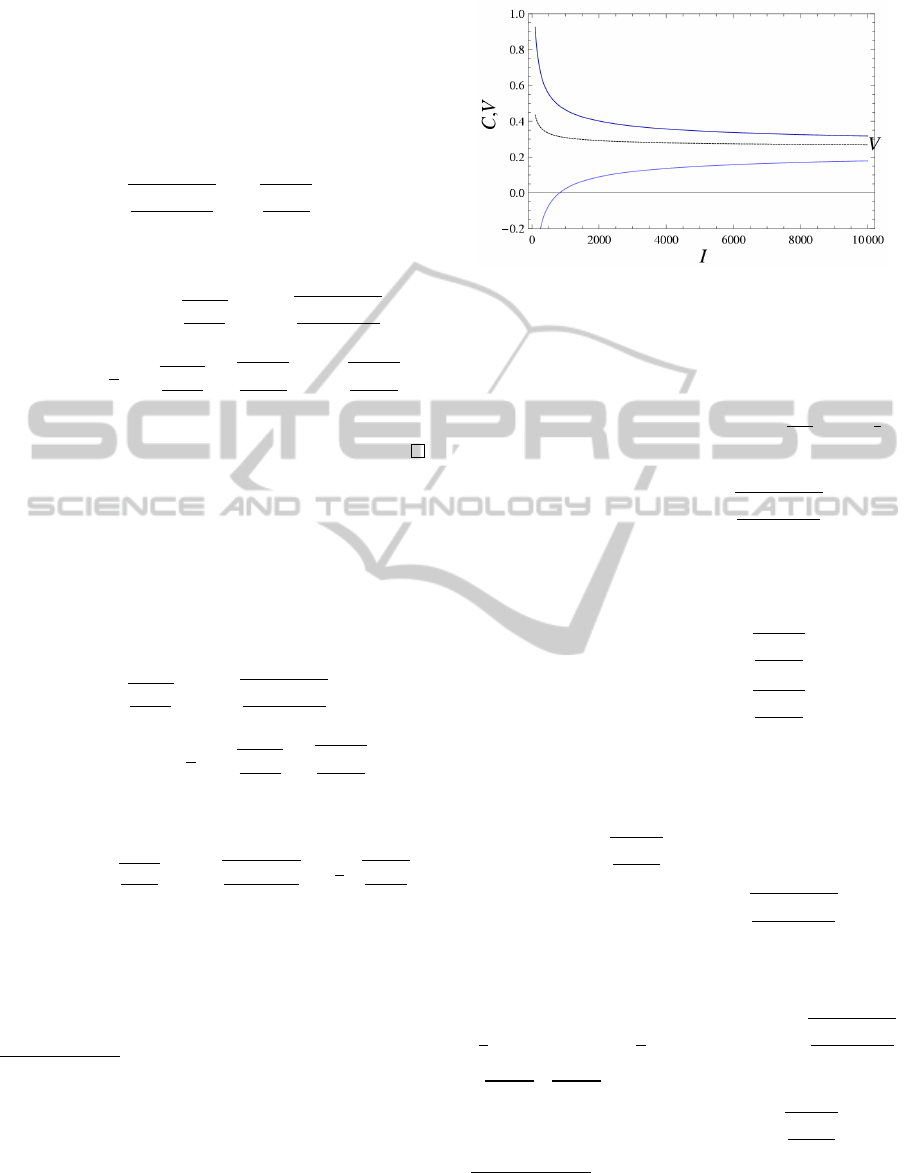
This is an important remark, because it means
that both the cross-validation result C and the Vapnik
bound V converge in probability
8
to the same value
9
as the sample size grows large. Moreover, the rate of
this convergence is exponential.
Proof of Remark 2. Since N is fixed, we note that
for η → 0
+
r
lnN −ln η
2I
∼
r
−lnη
2I
.
Therefore, for fixed η, N, n there exists a constant,
say D, such that
ε(η,I,N,n) = 2
r
n
n −1
+ 1
!
r
lnN −ln η
2I
+
√
n +
r
n
n −1
r
−lnη
2I
≤ D
r
−lnη
2I
.
Solving the inequality for η we obtain η ≤
exp(−2Iε
2
/D
2
).
Having in mind the inequality (16), we now give
two theorems in which the absolute value sign in
|V −C| is omitted. They can be viewed as the upper
and the lower probabilistic bounds on C and they are
derived as tighter bounds than (16). Proving these two
theorems immediately implies proving the theorem 1.
Theorem 2. With probability 1 −α(η,n) or greater,
the following inequality holds true:
C −V ≤
r
n
n −1
−1
!
r
lnN −ln η
2I
+
√
n +
r
n
n −1
r
−lnη
2I
. (17)
Theorem 3. With probability 1 −α(η,n) or greater,
the following inequality holds true:
V −C ≤
2
r
n
n −1
+ 1
!
r
lnN −lnη
2I
+
√
n
r
−ln η
2I
.
(18)
The second result is more interesting, provided of
course that the bound is positive for given constants
η, I, N, n. Otherwise, we get zero or negative bound,
which is trivial. The fig. 1 illustrates the sense of the-
orems 2 and 3.
8
We say that A(I) converges in probability to B, we write
A(I)
P
−→
I→∞
B, when for any numbers ε > 0, η > 0, there exists
a treshold size of sample I(ε, η), such that for all I ≥I(ε, η):
P
|A(I) −B| > ε
≤ η.
9
C and V can be viewed as random variables, due to ran-
dom realizations of data set {z
1
,. ..,z
I
} with joint density
p(z) (this affects C and V ) and due to random realizations
of subsets in cross-validation folds (this affects C). When
the data set {z
1
,. ..,z
I
} is fixed, V is fixed too.
Figure 1: Illustration of upper and lower bounds on the re-
sult of cross-validation with respect to the size of sample I.
Other constants are: η = 0.01 ⇒1 −α(η) ≈0.93, N = 100,
n = 3. With probability 1 −α(η) or greater, the result C of
cross-validation falls between the bounds.
Proof of Theorem 2. We remind: I
0
=
n−1
n
I, I
00
=
1
n
I.
With probability at least 1 − η, the following
bound on true risk holds true:
R(ω
I
0
) ≤ R
0
emp
(ω
I
0
) +
r
lnN −ln η
2I
0
. (19)
For the selected function ω
I
0
, fixed from now on,
Chernoff inequality is satisfied on the testing set (em-
pirical testing risk) in either of its one-side-versions:
R
00
emp
(ω
I
0
) −R(ω
I
0
) ≤
r
−lnη
2I
00
, (20)
R(ω
I
0
) −R
00
emp
(ω
I
0
) ≤
r
−lnη
2I
00
, (21)
with probability at least 1 −η each. By joining (19)
and (20) we obtain, with probability at least
10
1 −2η
the system of inequalities:
R
00
emp
(ω
I
0
) −
r
−lnη
2I
00
≤ R(ω
I
0
) ≤ R
0
emp
(ω
I
0
)
+
r
lnN −ln η
2I
0
. (22)
After n independent folds we obtain, with probability
at least (1 −2η)
n
:
1
n
n
∑
k=1
R
00
emp
(ω
I
0
,k
)
|
{z }
C
≤
1
n
n
∑
k=1
R
0
emp
(ω
I
0
,k
)+
r
lnN −ln η
2I
0
+
r
−lnη
2I
00
. (23)
10
The minimum probability must be 1 −2η rather than
(1 −η)
2
(probabilistic independence case) due to correla-
tions between inequalities. It can be also viewed as the con-
sequence of Bernoulli’s inequality.
A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF
LEARNING MACHINES
9

To conclude the proof, we need to relate some-
how R
0
emp
(ω
I
0
,k
) from each fold to R
emp
(ω
I
). We need
the relation in the direction R
0
emp
(ω
I
0
,k
) ≤ ···, so that
we can plug the right-hand-side of it into (23) and
keep it true. Intuitively, one might expect that choos-
ing an optimal function on a larger sample leads to a
greater empirical risk comparing to a smaller sample,
i.e. R
emp
(ω
I
) ≥R
0
emp
(ω
I
0
,k
), because it is usually eas-
ier to fit fewer data points using models of equally rich
complexities. But we don’t know with what probabil-
ity that occurs. Contrarily, on may easily find a spe-
cific data subset for which R
emp
(ω
I
) ≤ R
0
emp
(ω
I
0
,k
).
Lemma 1. With probability 1, true is the following
inequality:
I
0
∑
i=1
Q(z
0
i
,ω
I
0
) ≤
I
∑
i=1
Q(z
i
,ω
I
). (24)
On the level of sums of errors, not means, the
total error for a larger sample will always surpass
the total error for a smaller sample. This gives us
I
0
R
0
emp
(ω
I
0
) ≤ IR
emp
(ω
I
) and further:
R
0
emp
(ω
I
0
) ≤
n
n −1
R
emp
(ω
I
). (25)
Unfortunately it is of no use, because of the coeffi-
cient
n
n−1
. Thinking of C −V in the theorem, we need
a relation with coefficients 1 at both C and V .
In (Vapnik, 1995b, pp. 124) we find the following
helpful assertion:
Lemma 2. With probability at least 1 −2η:
Z
Z
Q(z,ω
I
)dF(z) − inf
1≤j≤N
Z
Z
Q(z,ω
j
)dF(z)
| {z }
R(ω
0
)
≤
r
lnN −ln η
2I
+
r
−lnη
2I
(26)
— the true risk for the selected function ω
I
is not far-
ther from the minimal possible risk for this set of func-
tions than
q
lnN−ln η
2I
+
q
−ln η
2I
.
Proof of that statement given by Vapnik is based
on two inequalities (each with probability at least 1 −
η), the first is (13) — we repeat it here, and the second
is Chernoff inequality for the best function ω
0
:
R(ω
I
) −R
emp
(ω
I
) ≤
r
lnN −ln η
2I
, (27)
R
emp
(ω
0
) −R(ω
0
) ≤
r
−lnη
2I
. (28)
And since, by definition of ω
I
, R
emp
(ω
0
) ≥R
emp
(ω
I
),
the (26) follows.
Going back to the cross-validation procedure, we
notice that in each single fold the measure R
emp
cor-
responds by analogy to the measure R in (26) and the
measure R
0
emp
corresponds by analogy to R
emp
therein.
Obviously R is defined on an infinite and continuous
space Z = X ×Y , whereas R
emp
is defined on a dis-
crete and finite sample {z
1
,.. .,z
I
}, but still from the
perspective of a single cross-validation fold we may
view R
emp
(ω
I
) as the “target” minimal probability of
misclassification and R
0
emp
(ω
I
0
) as the observed rela-
tive frequency of misclassification — an estimate of
that probability, remember that we take random sub-
sets {z
0
1
,.. .,z
0
I
0
} from the whole set {z
1
,.. .,z
I
}.
We write
R
0
emp
(ω
I
0
) ≤ R
0
emp
(ω
I
) ≤ R
emp
(ω
I
)+
r
−lnη
2I
0
. (29)
The first inequality is true with probability 1 by def-
inition of ω
I
0
. The second is a Chernoff inequality,
true with probability at least 1 −η.
Now, we plug (29) into (23) and obtain with prob-
ability 1 −(−
∑
n
k=1
n
k
(−1)
k
(2η)
k
) −η or greater:
C ≤
1
n
n
R
emp
(ω
I
) +
r
−lnη
2I
0
!
+
r
lnN −ln η
2I
0
+
r
−lnη
2I
00
= R
emp
(ω
I
) +
r
n
n −1
r
lnN −ln η
2I
+
√
n +
r
n
n −1
r
−lnη
2I
= R
emp
(ω
I
) +
r
n
n −1
+ 1 −1
!
r
lnN −ln η
2I
+
√
n +
r
n
n −1
r
−lnη
2I
= V +
r
n
n −1
−1
!
r
lnN −ln η
2I
+
√
n +
r
n
n −1
r
−lnη
2I
.
This concludes the proof of theorem 2.
Proof of Theorem 3. The proof is analogous to the
former proof, but we need to write most of the proba-
bilistic inequalities in the different direction.
With probability at least 1 − η, the following
bound on true risk holds true:
R
0
emp
(ω
I
0
) ≤ R(ω
I
0
) +
r
lnN −ln η
2I
0
. (30)
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
10

By joining (30) and (21) we obtain, with probabil-
ity at least 1 −2η the system of inequalities:
R
0
emp
(ω
I
0
) −
r
lnN −ln η
2I
0
≤ R(ω
I
0
) ≤ R
00
emp
(ω
I
0
)
+
r
−lnη
2I
00
. (31)
After n independent folds we obtain, with probability
at least (1 −2η)
n
:
1
n
n
∑
k=1
R
0
emp
(ω
I
0
,k
) −
r
lnN −ln η
2I
0
−
r
−lnη
2I
00
≤
1
n
n
∑
k=1
R
00
emp
(ω
I
0
,k
)
| {z }
C
. (32)
Again as in the former proof, we need to relate
R
0
emp
(ω
I
0
,k
) from each fold to R
emp
(ω
I
), but now we
need the relation to be in the direction R
0
emp
(ω
I
0
,k
) ≥
···, so that we can plug the right-hand-side of it into
(32) and keep it true.
We write
R
emp
(ω
I
)−
r
lnN −ln η
2I
0
≤R
emp
(ω
0
I
)−
r
lnN −ln η
2I
0
≤ R
0
emp
(ω
0
I
). (33)
Reading it from the right-hand-side: the second is a
(13)-like inequality but for discrete measures, which
is true with probability at least 1 −η, and the first in-
equality is true with probability 1 by definition of ω
I
.
Now, we plug (33) into (32) and obtain with prob-
ability 1 −(−
∑
n
k=1
n
k
(−1)
k
(2η)
k
) −η or greater:
C ≥
1
n
n
R
emp
(ω
I
) −
r
lnN −lnη
2I
0
!
−
r
lnN −lnη
2I
0
−
r
−ln η
2I
00
= R
emp
(ω
I
) −2
r
n
n −1
r
lnN −lnη
2I
−
√
n
r
−ln η
2I
= R
emp
(ω
I
) −
2
r
n
n −1
−1 + 1
!
r
lnN −lnη
2I
−
√
n
r
−ln η
2I
= V −
2
r
n
n −1
+ 1
!
r
lnN −lnη
2I
−
√
n
r
−ln η
2I
.
This concludes the proof of theorem 3.
Using theorems 2 and 3 we can also say what sam-
ple size I is necessary so that the the difference C −V
or V −C is less than or equal to an imposed epsilon
ε
∗
.
Let us denote the right-hand-sides of upper and
lower bounds (17) and (18) by ε
U
and ε
L
respectively.
Now, suppose we want to have ε
U
(η,I,N,n) ≤ ε
∗
U
.
Solving it for I we get
I ≥
1
2ε
∗
U
2
r
n
n −1
−1
p
lnN −ln η
+
√
n +
r
n
n −1
p
−lnη
!
2
(34)
Similarly, if we want to have ε
L
(η,I,N,n) ≤ ε
∗
L
.
I ≥
1
2ε
∗
L
2
2
r
n
n −1
+ 1
p
lnN −lnη +
√
n
p
−ln η
!
2
(35)
To give an example: say we have a finite set of
100 functions, N = 100, we perform a 5-fold cross-
validation, n = 5, and we choose η = 0.1 and ε
∗
L
=
ε
∗
U
= 0.05. Then it follows that we need a sample
of size I ≥ 5832 so that the cross-validation result is
not worse than V + 0.05, whereas we need I ≥ 28314
so that the cross-validation result is not better than
V −0.05. And both results are true with probability
1 −α(η,n) ≈ 0.73 or greater.
Remark 3. For the leave-one-out cross-validation,
where n = I, both the lower and the upper bound
loosen to a constant of order O
q
−ln η
2
.
Actually, one can easily see that as we take larger
samples I → ∞ and we stick to the leave-one-out
cross-validation n = I, the coefficient
q
n
n−1
standing
at
q
lnN−ln η
2I
goes to 1, whereas the coefficient
√
n
standing at
q
−ln η
2I
goes to infinity.
One might ask: for what choice of n each bound
is the tightest given η, I, N? Treating for a moment n
as a continuous variable, we impose the conditions:
∂ε
U
(η,I,N,n)
∂n
= 0,
∂ε
L
(η,I,N,n)
∂n
= 0,
and we get optimal n values:
n
∗
U
= 1 +
√
lnN −ln η +
√
−lnη
√
−lnη
!
2
3
, (36)
n
∗
L
= 1 +
2
√
lnN −ln η
√
−lnη
!
2
3
. (37)
Note that these values do not depend on the sample
size I.
A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF
LEARNING MACHINES
11

2.2 Regression Estimation Learning
Task
Now we consider the set of real-valued error func-
tions but we still stay with the simplest case when the
set has a finite number of elements. We give theorems
for the regression estimation learning task, analogous
to the ones for the classification. We skip proofs —
the only changes they would require is the assumption
of the bounded functions, and the use of Hoeffding in-
equality in the place of Chernoff inequality.
Theorem 4. Let {Q(z,ω
j
)}
ω
j
∈Ω
, j = 1,2,... ,N, be a
finite set of real-valued bounded functions (regression
estimation task) of size N, 0 ≤Q(z,ω
j
) ≤B. Then, for
any η > 0, arbitrarily small, there is a small number
α(η,n) = η −
n
∑
k=1
n
k
(−1)
k
(2η)
k
, (38)
and the number
ε(η,I,N,n) =
2
r
n
n −1
+ 1
!
B
r
lnN −ln η
2I
+
√
n +
r
n
n −1
B
r
−lnη
2I
, (39)
such that:
P
|V −C| ≤ ε(η,I,N,n)
!
≥ 1 −α(η, n). (40)
Theorem 5. With probability 1 −α(η,n) or greater,
the following inequality holds true:
C −V ≤
r
n
n −1
−1
!
B
r
lnN −ln η
2I
+
√
n +
r
n
n −1
B
r
−lnη
2I
. (41)
Theorem 6. With probability 1 −α(η,n) or greater,
the following inequality holds true:
V −C ≤
2
r
n
n −1
+ 1
!
B
r
lnN −lnη
2I
+ B
√
n
r
−ln η
2I
.
(42)
3 THE RELATIONSHIP FOR AN
INFINITE SET OF
APPROXIMATING FUNCTIONS
The simplest case with a finite number of functions
in the set has been generalized by Vapnik (Vapnik,
1995b; Vapnik and Chervonenkis, 1989; Vapnik and
Chervonenkis, 1968) onto infinite sets with contin-
uum of elements by introducing several notions of the
capacity of the set of functions: entropy, annealed en-
tropy, growth function, Vapnik–Chervonenkis dimen-
sion. We remind them in brief.
First of all, Vapnik defines N
Ω
(z
1
,.. .,z
I
) which
is the number of all possible dichotmies that can be
achieved on a fixed sample {z
1
,.. .,z
I
} using func-
tions from {Q(z,ω)}
ω∈Ω
. Then, if we relax the sam-
ple the following notions of capacity can be consid-
ered:
1. expected value of ln N
Ω
— Vapnik-Chervonenkis
entropy:
H
Ω
(I) =
Z
z
1
∈Z
···
Z
z
I
∈Z
lnN
Ω
(z
1
,.. .,z
I
)
·p(z
1
)···p(z
I
)dz
1
···dz
I
,
2. ln of expected value of N
Ω
— annealed entropy:
H
Ω
ann
(I) = ln
Z
z
1
∈Z
···
Z
z
I
∈Z
N
Ω
(z
1
,.. .,z
I
)
·p(z
1
)···p(z
I
)dz
1
···dz
I
,
3. ln of supremum of N
Ω
— growth function
G
Ω
(I) = ln sup
z
1
,...,z
I
N
Ω
(z
1
,.. .,z
I
).
It has been proved that:
G
Ω
(I) =
(
= ln 2
I
, dla I ≤ h;
≤ ln
∑
h
k=0
I
k
, dla I > h,
(43)
where h is the Vapnik–Chervonenkis dimension.
It has been shown (Vapnik, 1995b) that
H
Ω
(I)
(Jensen)
≤ H
Ω
ann
(I) ≤ G
Ω
(I) ≤ ln
h
∑
k=0
I
k
≤ ln
eI
h
h
= h(1 + ln
I
h
). (44)
And the right-hand-side of (44) can be suitably in-
serted in the bounds to replace lnN.
We mention that appropriate generalizations from
the set of indicator functions (classification) onto sets
of real-valued functions (regression estimation) can
be found in (Vapnik, 1995b) and are based on the no-
tions of: ε-finite net, set of classifiers for a fixed real-
valued f , complete set of classifiers for Ω.
3.1 Classification Learning Task
(Infinite Set of Functions)
For shortness, we give only two theorems for bounds
on V −C and C −V , the bound on |V −C| is their
straightforward consequence (analogically as in pre-
vious sections).
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
12

Theorem 7. Let {Q(z,ω)}
ω∈Ω
be an infinite set of
indicator functions with finite Vapnik–Chervonenkis
dimension h. Then, with probability 1 −α(η,n) or
greater, the following inequality holds true:
C −V ≤
r
n
n −1
−1
!
s
h(1 +
2I
h
) −ln
η
4
I
+
√
n +
r
n
n −1
r
−lnη
2I
. (45)
Theorem 8. With probability 1 −α(η,n) or greater,
the following inequality holds true:
V −C ≤
2
r
n
n −1
+ 1
!
s
h(1 +
2I
h
) −ln
η
4
I
+
√
n
r
−lnη
2I
. (46)
3.2 Regression Estimation Learning
Task (Infinite Set of Functions)
Again, for shortness, we give only two theorems for
bounds on V −C and C −V , the bound on |V −C| is
their straightforward consequence (analogically as in
previous sections).
Theorem 9. Let {Q(z,ω)}
ω∈Ω
be an infinite set of
real-valued bounded functions, 0 ≤ Q(ω,z) ≤ B, with
finite Vapnik–Chervonenkis dimension h. Then, with
probability 1 −α(η,n) or greater, the following in-
equality holds true:
C −V ≤
r
n
n −1
−1
!
B
s
h(1 +
2I
h
) −ln
η
4
I
+
√
n +
r
n
n −1
r
−lnη
2I
. (47)
Theorem 10. With probability 1 −α(η,n) or greater,
the following inequality holds true:
V −C ≤
2
r
n
n −1
+ 1
!
B
s
h(1 +
2I
h
) −ln
η
4
I
+
√
n
r
−lnη
2I
. (48)
In practice, bounds (47) and (48) can be signifi-
cantly tightened by using an estimate
b
B in the place of
the most pessimistic B. The estimate
b
B can be found
by performing just one fold of cross-validation (in-
stead of n folds) and bounding
b
B by: mean error on
the testing set plus a square root implied by the Cher-
noff inequality:
b
B ≤ R
00
emp
(ω
0
I
) + B
r
−lnη
B
2I
00
, (49)
where η
B
is an imposed small probability that (49)
is not true. The reasoning behind this remark is that
in practice, typical learning algorithms rarely produce
functions f (x, ω
I
), in the process of ERM, having
high maximal errors. Therefore, we can insert the
right-hand-side of (49) into (47) and (48) in the place
of B. If this is done, then the minimal overall proba-
bility on bounds (47) and (48) should be adjusted to
1 −α(η,n) −η
B
.
4 EXPERIMENTS — BOUNDS
CHECKS
Results of three experiments are shown in this section,
for the following cases: (1) binary classification, finite
set of functions, (2) binary classification, infinite set
of functions, (3) regression estimation, infinite set of
functions.
4.1 Set of Functions
The form of f functions, f : [0,1]
2
→ [−1, 1], was
Gaussian-like:
f (x, w0,w
1
,.. .,w
K
| {z }
ω
) =
max
−1,min
1,w
0
+
K
∑
k=1
w
k
exp
−
kx −µ
k
k
2
2σ
k
2
(50)
where centers µ
k
and widths σ
k
were generated on
random
11
and remained fixed. Therefore we have a set
of functions linear in parameters (w
0
,w
1
,.. .,w
K
). As
one can see values of f where constrained by ±1. For
the classification learning task, the decision boundary
was arising as the solution of f (x,w
0
,w
1
,.. .,w
K
) =
0. For the regression estimation, we simply looked at
the values of f (x,w
0
,w
1
,.. .,w
K
). Examples of func-
tions from this set are shown in figures 2, 3
4.2 System and Data Sets
As a system y(x) we picked on random a function
from a similar class to (50) but broader, in the sense
11
Random intervals: µ
k
∈ [0, 1]
2
, σ
k
∈ [0.02, 0.1].
A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF
LEARNING MACHINES
13

{
, , ,··· ,
}
Figure 2: Illustration of the set of functions for classification.
{
, , ,··· ,
}
Figure 3: Illustration of the set of functions for regression estimation.
that the number K was greater and the range of ran-
domness on σ
k
was larger. Data sets for both classifi-
cation and regression estimation were taken by sam-
pling the system according to the joint probability
density p(x,y) = p(x)p(y|x) where we set p(x) = 1
— uniform distribution on the domain [0,1]
2
and
p(y|x) =
1
√
2πσ
exp(−
(y−y(x))
2
2σ
2
) — normal noise with
σ = 0.1.
Figure 4: System and data for classification (a, b), regres-
sion estimation (c, d).
4.3 Algorithm of the Learning Machine
In the case of finite sets of N functions, the learn-
ing machine was simply choosing the best functions
as f (ω
I
) = argmin
j=1,2,...,N
R
emp
(ω
j
) or in cross-
validation folds f (ω
I
0
) = argmin
j=1,2,...,N
R
0
emp
(ω
j
).
In the case of infinite sets with continuum of
elements, the learning machine was trained by the
least-squares criterion. We remark that obviously
other learning approaches can be used in this place
e.g. maximum likelihood, SVM criterion (Vapnik,
1995b; Vapnik, 1995a; M. Korze
´
n and Kl˛esk, 2008).
If we denote the bases exp
−
kx−µ
k
k
2
2σ
k
2
by g
k
(x) and
calculate the matrix of bases at data points
G =
1 g
1
(x
1
) g
2
(x
1
) ··· g
K
(x
1
)
1 g
1
(x
2
) g
2
(x
2
) ··· g
K
(x
2
)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1 g
1
(x
I
) g
2
(x
I
) ··· g
K
(x
I
)
(51)
we can find the optimal vector of w coefficients by the
pseudo-inverse operation as follows:
(w
0
,w
1
,.. .,w
K
)
T
= (G
T
G)
−1
G
T
Y, (52)
where Y = (y
1
,y
2
,.. .,y
I
)
T
is a vector of training tar-
get values.
4.4 Experiment Results and Comments
Experiments involved trying out different settings on
all relevant constants such as: number of terms in ap-
proximating functions (K), number of functions (N)
in the case of finite sets or VC dimension (h) in case
of infinite sets, sample size (I), number of cross-
validation folds (n). For each fixed setting of the con-
stants, an experiment with repetitions was performed,
during which we measured the cross-validation out-
come C after each repetition. The range of these out-
comes was then compared to the interval implied by
the theorems we proved.
We show the results in two tables 1 and 2. The first
one gives an insight on details of a single exemplary
experiment: results of its particular folds and repeti-
tions. The second one shows collective results, where
each row encapsulates 10 repetitions
12
.
12
It was difficult to allow ourselves for more repeti-
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
14

Table 2: Collective results — each row encapsulates 10 repetitions. Tasks: c. — classification, r.e. — regression estimation.
We denote experiments on finite or infinite sets of functions by setting either N or h. For regression estimation we use
probabilistic
b
B calculated as R
00
emp
(ω
0
I
) + B
p
−ln η
B
/(2I
00
). In all experiments η = 0.2, hence for n = 3 the probability that
bounds are true is 1 −α(η,n) = 0.496 or greater and for n = 5 it is 1 −α(η,n) = 0.511 or greater.
no.
of
exp. task K N h I R
emp
(ω
I
) V n
bounds
[V −ε
L
,V + ε
U
]
observed
range of C
(10 repetitions)
ratio of
C inside
bounds
1 c. 50 10 - 10
3
0.412 0.456 3 [0.254,0.550] [0.351,0.445] 1.0
2 c. 200 10 - 10
3
0.345 0.389 3 [0.187,0.483] [0.352,0.385] 1.0
3 c. 200 10 - 10
4
0.369 0.383 3 [0.319,0.413] [0.371,0.383] 1.0
4 c. 200 10 - 10
4
0.396 0.410 5 [0.344,0.442] [0.386,0.401] 1.0
5 c. 50 100 - 10
4
0.408 0.426 3 [0.349,0.456] [0.392,0.418] 1.0
6 c. 200 100 - 10
4
0.336 0.354 3 [0.277,0.384] [0.332,0.338] 1.0
7 c. 50 100 - 10
5
0.401 0.407 3 [0.383,0.417] [0.398,0.403] 1.0
8 c. 50 - 51 10
5
0.181 0.250 3 [0.021,0.267] [0.181,0.184] 1.0
9 c. 200 - 201 10
5
0.035 0.161 3 [−0.25,0.185] [0.035,0.037] 1.0
9 r.e. 50 -
51
(
b
B = 0.193) 10
4
0.172 0.209 3 [0.078,0.223] [0.170,0.173] 1.0
10 r.e. 50 -
51
(
b
B = 0.194) 10
4
0.171 0.208 5 [0.085,0.212] [0.170,0.172] 1.0
11 r.e. 200 -
201
(
b
B = 0.020) 10
5
0.012 0.015 3 [0.006,0.016] [0.012,0.013] 1.0
12 r.e. 200 -
201
(
b
B = 0.020) 10
5
0.013 0.015 5 [0.007,0.016] [0.012,0.013] 1.0
Table 1: Details (folds, repetitions) of an exemplary exper-
iment no. 1.
no. of
expe-
riment repetition fold R
0
emp
(ω
I
0
)
is
ω
I
0
= ω
I
? R
00
emp
(ω
I
00
)
1 1 1 0.397 false 0.444
1 1 2 0.418 true 0.369
1 1 3 0.400 false 0.468
C = 0.417
1 2 1 0.359 true 0.369
1 2 2 0.374 true 0.339
1 2 3 0.370 true 0.348
C = 0.352
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1 10 1 0.403 true 0.384
1 10 2 0.395 true 0.399
1 10 3 0.394 true 0.399
C = 0.394
To comment on the results we first remark that
before each single experiment (1-12) the whole data
set was drawn once from p(z) and remained fixed
throughout repetitions. However, in the repetitions
due to the non-stratified cross-validation we parted
the data set (via permutations) into different training
and testing subsets. That is why in the table R
emp
(ω
I
)
and V are constant per experiment, whereas the cross-
validation varies within some observed range. In the
tions, say 100, due to large amount of results and the time-
consumption of each experiment. Yet, the observed ratio
1.0 of C falling inside bounds shows that 10 repetitions was
sufficient.
table 2 we also present the interval [V −ε
L
,V + ε
U
]
which is implied by the theorems.
Please note that for all experiments the observed
range for C was contained inside [V −ε
L
,V + ε
U
] —
an empirical confirmation of theoretical results. Al-
though the bounds are true with probability at least
1 − α(η,n), in this particular experiment they held
with frequency one.
In particular one can note in the table that the up-
per bounds V + ε
U
are closer to actual C outcomes,
while lower bounds V +ε
L
are more loose — a fact we
already indicated in theoretical sections. Only in the
case of experiment no. 9 the lower bound we obtained
was trivial. In the results one can also observe the
qualitative fact that both intervals tighten with 1/
√
I
approximately. Keep in mind that this result stops
working for the ‘leave-one-out’ cross-validation (or a
close one) and we experimented on n = 3 and n = 5.
5 EXPERIMENTS — SRM
In this section we show results of the Structural Risk
Minimization approach. We consider a structure i.e. a
sequence of nested subsets of functions: S
1
⊂ S
2
⊂
··· ⊂ S
K
, where each successive S
k
=
f (x, ω)
ω∈Ω
k
is a set of functions with Vapnik-Chervonenkis di-
mension h
k
, and we have h
1
< h
2
< ··· < h
K
. As the
best element of the structure we choose S
∗
(with VC
dimension h
∗
) for which the bound on generalization
V is the smallest.
A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF
LEARNING MACHINES
15
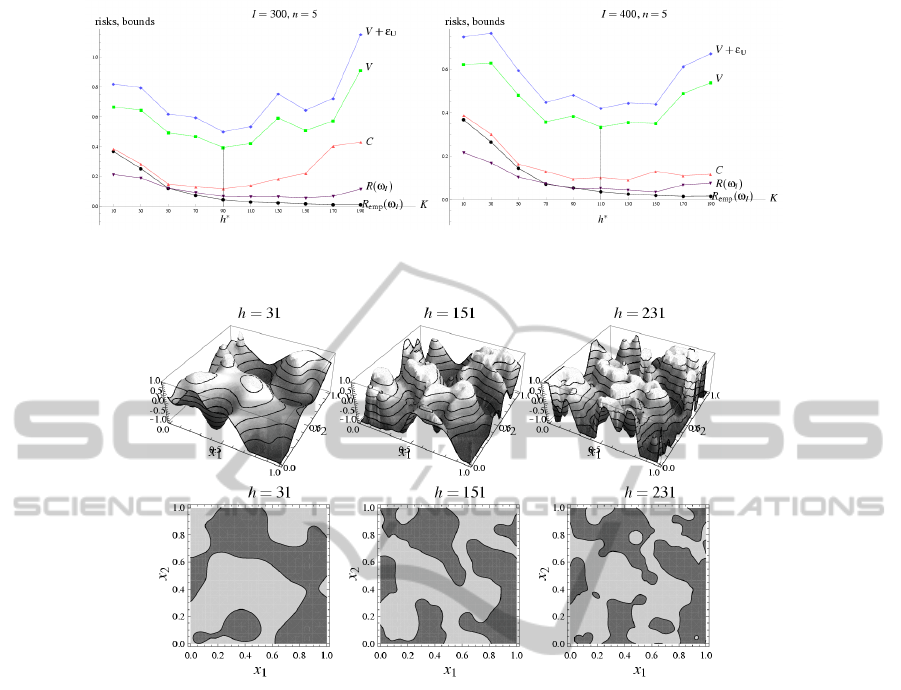
Figure 5: SRM experiments. With I = 300, optimum points reached at: h
∗
= 91 (SRM), h = 91 (C), h = 151 (true risk R).
With I = 400, optimum points reached at: h
∗
= 111 (SRM), h = 131 (C), h = 151 (true risk R).
Figure 6: Exemplary models for both regresssion estimation and classfication: under complex (h = 31), accurately complex
— the best generalization (h = 151), over complex (h = 231).
Along with observing the bound V , we observe:
(1) the cross-validation result C, (2) our bounds on
C, (3) the actual true risk R calculated as an inte-
gral according to its definition (1). We pay particu-
lar attention to how the minimum point of SRM at
h
∗
differs from the minimum suggested by the cross-
validation and the minimum of true risk (which nor-
mally in practice is unknown). We remind that ob-
taining the result C for each h
k
is O(n) times more
laborious than obtaining V for each h
k
. See fig. 5.
6 SUMMARY
In the paper we take under consideration the proba-
bilistic relationship between two quantities: Vapnik
generalization bound V and the result C of an n-fold
non-stratified cross-validation. In the literature on the
subject of machine learning (and SLT) typically the
stated results have a different focus — namely, the re-
lation between the true risk (generalization error) and
either of the two quantities V , C separately. The per-
spective we chose was intended to:
- stay in the setting of Structural Risk Minimization
approach based on Vapnik bounds,
- not perform the cross-validation procedure,
- be able to make probabilistic statements about
closeness of SRM results to cross-validation re-
sults (if such was perfomed) for given conditions
of learning experiment.
Suitable theorems about this relationship are
stated and proved. The theorems concern two learn-
ing tasks: classification and regression estimation;
and also two cases as regards the capacity of the set of
approximating functions: finite sets and infinite sets
(but with finite Vapnik-Chervonenkis dimension).
As the sample size grows large, both C and V con-
verge in probability to the same limit of true risk. The
rate of convergence is exponential.
Using the theorems, one can find a threshold size
of sample so that the difference C −V or V −C is
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
16

smaller than an imposed ε. Obviously, the smaller ε
for given experiment conditions, the more frequently
one can expect to select the same optimal model com-
plexity via SRM and via cross-validation (again with-
out actually performing it).
For the special case of leave-one-out cross-
validation we observe in the consequence of bounds
we derived that at most a constant difference of order
O(
p
−lnη/2) between C and V can be expected.
Additionally, we showed for what number n of
folds, the bounds (lower and upper) on the difference
are the tightest. Interestingly, as it turns out these op-
timal n values do not depend on the sample size.
Finally, shown are experiments confirming statis-
tical correctness of the bounds.
ACKNOWLEDGEMENTS
This work has been financed by the Polish Govern-
ment, Ministry of Science and Higher Education from
the sources for science within years 2010–2012. Re-
search project no.: N N516 424938.
REFERENCES
Anthony, M. and Shawe-Taylor, J. (1993). A result of vap-
nik with applications. Discrete Applied Mathematics,
47(3):207–217.
Bartlett, P. (1997). The sample complexity of pattern clas-
sification with neural networks: the size of weights is
more important then the size of the network. IEEE
Transactions on Information Theory, 44(2).
Bartlett, P., Kulkarni, S., and Posner, S. (1997). Covering
numbers for real-valued function classes. IEEE Trans-
actions on Information Theory, 47:1721–1724.
Cherkassky, V. and Mulier, F. (1998). Learning from data.
John Wiley & Sons, inc.
Devroye, L., Gyorfi, L., and Lugosi, G. (1996). A Proba-
bilistic Theory of Pattern Recognition. Springer Ver-
lag, New York, inc.
Efron, B. and Tibshirani, R. (1993). An Introduction to the
Bootstrap. London: Chapman & Hall.
Fu, W., Caroll, R., and Wang, S. (2005). Estimating mis-
classification error with small samples via bootstrap
cross-validation. Bioinformatics, 21(9):1979–1986.
Hellman, M. and Raviv, J. (1970). Probability of error,
equivocation and the chernoff bound. IEEE Transac-
tions on Information Theory, IT-16(4):368–372.
Hjorth, J. (1994). Computer Intensive Statistical Methods
Validation, Model Selection, and Bootstrap. London:
Chapman & Hall.
Holden, S. (1996a). Cross-validation and the pac learning
model. Technical Report RN/96/64, Dept. of CS, Uni-
versity College, London.
Holden, S. (1996b). Pac-like upper bounds for the sample
complexity of leave-one-out cross-validation. In 9-th
Annual ACM Workshop on Computational Learning
Theory, pages 41–50.
Kearns, M. (1995a). A bound on the error of cross-
validation, with consequences for the training-test
split. In Advances in Neural Information Processing
Systems 8. MIT Press.
Kearns, M. (1995b). An experimental and theoretical com-
parison of model selection methods. In 8-th Annual
ACM Workshop on Computational Learning Theory,
pages 21–30.
Kearns, M. and Ron, D. (1999). Algorithmic stabil-
ity and sanity-check bounds for leave-one-out cross-
validation. Neural Computation, 11:1427–1453.
Kohavi, R. (1995). A study of cross-validation and boostrap
for accuracy estimation and model selection. In In-
ternational Joint Conference on Artificial Intelligence
(IJCAI).
Krzy
˙
zak, A. et al. (2000). Application of structural risk min-
imization to multivariate smoothing spline regression
estimates. Bernoulli, 8(4):475–489.
M. Korze
´
n, M. and Kl˛esk, P. (2008). Maximal mar-
gin estimation with perceptron-like algorithm. In
L. Rutkowski, R. Tadeusiewicz R., L. Z. J. Z., editor,
Lecture Notes in Artificial Intelligence, pages 597–
608. Springer.
Ng, A. (2004). Feature selection, l1 vs. l2 regularization,
and rotational invariance. In 21-st International Con-
ference on Machine learning, ACM International Con-
ference Proceeding Series, volume 69.
Schmidt, J., Siegel, A., and Srinivasan, A. (1995).
Chernoff-hoeffding bounds for applications with lim-
ited independence. SIAM Journal on Discrete Mathe-
matics, 8(2):223–250.
Shawe-Taylor, J. et al. (1996). A framework for structural
risk minimization. COLT, pages 68–76.
Vapnik, V. (1995a). The Nature of Statistical Learning The-
ory. Springer Verlag, New York.
Vapnik, V. (1995b). Statistical Learning Theory: Inference
from Small Samples. Wiley, New York.
Vapnik, V. (2006). Estimation of Dependences Based on
Empirical Data. Information Science & Statistics.
Springer, US.
Vapnik, V. and Chervonenkis, A. (1968). On the uniform
convergence of relative frequencies of events to their
probabilities. Dokl. Aka. Nauk, 181.
Vapnik, V. and Chervonenkis, A. (1989). The necessary
and sufficient conditions for the consistency of the
method of empirical risk minimization. Yearbook of
the Academy of Sciences of the USSR on Recognition,
Classification and Forecasting, 2:217–249.
Weiss, S. and Kulikowski, C. (1991). Computer Systems
That Learn. Morgan Kaufmann.
A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF
LEARNING MACHINES
17
