
AN ABM OF THE DEVELOPMENT OF SHARED MEANING
IN A SOCIAL GROUP
Enrique Canessa, Sergio E. Chaigneau
Facultad de Ingeniería y Ciencias & Centro de Investigación de la Cognición, Universidad Adolfo Ibáñez
Balmaceda 1625, Recreo, Viña del Mar, Chile
Escuela de Psicología & Centro de Investigación de la Cognición, Universidad Adolfo Ibáñez
Diagonal Las Torres 2640, Peñalolén, Santiago, Chile
Ariel Quezada
Escuela de Psicología & Centro de Investigación de la Cognición, Universidad Adolfo Ibáñez
Balmaceda 1625, Recreo, Viña del Mar, Chile
Keywords: Agent-based modelling, Shared meaning, Conceptual content, Markov chain.
Abstract: Generally, concepts are treated as individual-level phenomena. Here, we develop an ABM that treats
concepts as group-level phenomena. We make simple assumptions: (1) Different versions exist of one
similar conceptualization; (2) When we infer that our view agrees with someone else’s view, we are subject
to true agreement (i.e., we really share the concept), but also to illusory agreement (i.e., we do not really
share the concept); (3) Regardless whether agreement is true or illusory, it strengthens a concept’s salience
in individual minds, and increases the probability of seeking future interactions with that person or source of
information. When agents interact using these rules, our ABM shows that three conditions exist: (a) All
versions of the same conceptualization strengthen their salience; (b) Some versions strengthen while others
weaken their salience; (c) All versions weaken their salience. The same results are corroborated by
developing probability models (conditional and Markov chain). Sensitivity analyses to various parameters,
allow the derivation of intuitively correct predictions that support our model’s face validity. We believe the
ABM and related mathematical models may explain the spread or demise of conceptualizations in social
groups, and the emergence of polarized social views, all important issues to sociology and psychology.
1 INTRODUCTION
Concepts appear to have a life-cycle in the cultures
in which they exist. Concepts are born at a certain
point in time, spread or not through culture, and die
out. Our view here is that the fate of concepts in
culture depends on their usefulness, and that a
concept is useful when it generates episodes of
shared meaning, thus allowing social cohesion and
the coordination of behaviour. Given that meaning is
something that happens in individual minds, how is
it possible that people agree about a meaning?
Psychological inquiry often assumes that meaning is
shared by resorting to direct reference, i.e., by
pointing to the referred object, rather than by
describing it (Brennan & Clark, 1996; Brown-
Schmidt & Tanenhaus, 2008; Carpenter, Nagell, &
Tomasello, 1998; Clark & Krych, 2004; Galantucci
& Sebanz, 2009; Garrod & Anderson, 1987; Moses,
Baldwin, Rosicky, & Tidball, 2001; Richardson,
Dale & Tomlinson, 2009; Tomasello, 1995). Though
this approach may work for concrete objects, it does
not solve the problem of how people agree about the
meaning of diffuse objects (abstract entities like,
e.g., democracy, womanhood, happiness). Direct
reference does not apply for these objects because
they lack clear spatio-temporal limits, thus
preventing the use of direct reference in interactions.
Furthermore, everyday concepts like those
illustrated above are notoriously ill-defined; making
shared meaning even more mysterious (Rosch &
Mervis, 1975). In our current work, we hold the
view that shared meaning is possible because
meaning is conventional, i.e., there is a limited set of
5
Canessa E., Chaigneau S. and Quezada A..
AN ABM OF THE DEVELOPMENT OF SHARED MEANING IN A SOCIAL GROUP .
DOI: 10.5220/0003120100050014
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 5-14
ISBN: 978-989-8425-41-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

meanings that apply to a given situation (Lewis,
1969; Lewis, 1975; Millikan, 2005). Constraining
the number of concepts that apply on a given
occasion, makes agreement a tractable problem.
However, even if a group of people has developed
conceptual conventions, the likely case is that each
person instantiates a somewhat different version of
those concepts (e.g., people may conceptualize
“leadership” in slightly different ways).
Furthermore, even if a group of people has
conventions about more or less dichotomous
concepts (e.g., “cowardice” and “courage”), a person
could still be wrong about which one is being
deployed by someone else at a given moment (e.g.,
if someone says “suicide”, she may be thinking of
“cowardice” while I may be thinking of “courage”).
Consequently, an individual can never know for sure
whether someone else agrees or not with his
conceptualization of a given event (even when being
explicit). Agreement is a probabilistic inference
(Chaigneau & Gaete, in preparation).
The ABM we report here focuses on two
probabilities that represent the abovementioned
inference. First, the probability of true agreement
(symbolized by p(a1)), which stands for the
probability that two agents (an observer and an
actor) agree on something given that they instantiate
different versions of the same concept (i.e., the
“leadership” example above). Second, the
probability of illusory agreement (symbolized by
p(a2)), which stands for the probability that observer
and actor agree, given that they instantiate different
concepts altogether (i.e., the “courage” or
“cowardice” example above).
2 CONCEPTUAL DESCRIPTION
OF THE ABM
Our current ABM represents a social group which
has a set of conventional conceptual states that, for
ease of exposition, we will call the focal set. These
states can represent different versions of the same
concept (e.g., different versions of “leadership”; or a
set of closely related concepts, such as “miserly”,
“stingy”, “scrooge”). Our p(a1) probability reflects
the degree of overlap between the different versions
in the focal set (greater overlap implies greater
probability of true agreement). Our p(a2) probability
reflects the degree of contrast against alternative
conceptualizations (lower contrast implies greater
probability of illusory agreement). The system
models the dynamical trajectories of concepts as
they become increasingly or decreasingly relevant
for agents depending on their capacity to generate
agreement of any type.
In each simulation run, agents act as observers
and actors. Observers seek evidence that actors share
their concept. Actors have a certain probability that
they will or will not act according to the focal set
concept. If they act according to the focal set
concept, that specific interaction has a probability
p(a1) of providing observers evidence of a shared
concept. If actors don’t act according to the focal set
concept (i.e., they act according to the contrast
concept), that specific interaction has a probability
p(a2) of providing observers evidence of a shared
concept.
We make some very simple and quite generally
accepted assumptions about our agents’ psychology.
If the observer witnesses evidence (blind to whether
it is true or illusory agreement), then his own
conceptual state increases its relevance in his mind
(i.e., our cognitive assumption; c.f., Evans, 2008;
Brewer, 1988; Lenton, Blair & Hastie, 2002), will be
more likely to guide his behaviour in the future (i.e.,
our motivational assumption; c.f., Rudman &
Phelan, 2008), and the observer will want to interact
with that particular agent again in the future (i.e., our
social assumption; c.f., Nickerson, 1998).
3 ABM IMPLEMENTATION
The theory presented in section 2 is implemented in
an agent-based model (ABM). In summary, the
ABM represents how concepts spread and get
stronger (or weaker) in a social group, by observing
the behaviour of other members. In the ABM, each
individual is an agent (actor, A), which acts
according to its concept with probability equal to the
strength of the concept. That behaviour is observed
by another agent (observer, O), and that changes the
strength of its concept. In general, if the observed
behaviour agrees with the behaviour expected from
O’s concept, then O’s concept strengthens.
Conversely, if the observed behaviour differs from
what is expected from that concept, then O’s concept
weakens. Concurrently, the agents begin to interact
more frequently with those that have strengthened
their concepts. In the following paragraphs we
describe the details of the ABM.
In the social group that the ABM represents, one
can set the number of members that belong to the
group. Each agent can have one of five different
related concepts or versions of the same concept and
each of the concepts or versions is represented by a
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
6

number in the [0, 1] interval, labelled the coefficient
of the concept. This coefficient determines the
probability that an agent behaves according to the
given concept. The initial values of the coefficients
are sampled from a normal distribution with a mean
and standard deviation, which can be set. The model
checks that the assigned coefficients will always
remain in the [0, 1] interval.
Agents modify the strength of their concept’s
coefficients by observing the behaviour of other
agents. Every time they see behaviour consistent
with their concepts, the corresponding coefficients
are incremented by 0.02. On the other hand, if the
observed behaviour is not consistent with their
concepts, the corresponding coefficients are
decremented by 0.02. The model makes sure that the
coefficients always remain inside the [0, 1] interval.
Thus, when an agent sees that another agent acts
according to its concept, it is more probable that the
agent will act according to its own concept in the
future. These actions spread concepts throughout the
group.
Agents develop interaction preferences as they
observe each other. Specifically, agents will tend to
interact more frequently with agents who have
confirmed their concepts in previous interactions,
and indirectly, they will be less likely to interact
with those that have not confirmed their concepts.
This aspect of the ABM limits the diffusion of
concepts, given that it imposes certain heterogeneity
to the diffusion speed of the concepts. It could even
cause the weakening of some concepts among
certain members of the group. To simulate this
aspect of our theory, each agent has an interaction
probability with the rest of the agents. Taking into
account computational restrictions, those
probabilities take only discrete values (0.08, 0.11,
0.17, 0.26 and 0.38, probabilities which increase by
approximately 50% between successive values). At
the start of a simulation run, all the agents are
assigned a probability equal to 0.08, which means
that an agent will randomly interact with any other
agent. Then, as the run advances, if agent A
confirms O’s concept, agent O will increase its
interaction probability with A to the immediately
larger value. For example, if agent A’s interaction
probability was 0.08, then agent A will increase that
probability to 0.11.
A last aspect incorporated in the ABM is that in a
social group, it might exist more than one version of
a concept. Thus, the model allows setting the
number of versions that will be present in a group
between 1 and 5. Each version will be assigned to a
number of agents equal to the total number of agents
in a group divided by the number of versions.
Each agent O determines whether its concept
will strengthen or weaken according to the following
rules:
a) If A acts according to its own concept in the
focal set, and A’s conceptual content completely
coincides with O’s conceptual content, then O’s
concept will strengthen with probability equal to 1.
b) If A acts according to its own concept in the
focal set, and that concept is a version of the same
concept in O’s focal set (but not identical), then O’s
concept will strengthen with probability equal to
p(a1)and will weaken with probability equal to 1 -
p(a1).
c) If A does not act according to its concept in the
focal set (i.e., acts according to a contrasting
concept), and the contrasting concept overlaps
somewhat with the O’s concept in the focal set, then
O’s concept will strengthen with probability equal to
p(a2) and will weaken with probability equal to 1 -
p(a2).
d) If A does not act according to its concept in the
focal set (i.e., acts according to a contrasting
concept), and A’s conceptual content completely
coincides with O’s conceptual content, then O’s
concept will weaken with probability equal to 1.
Finally, each simulation cycle or step of the ABM is
composed of the following actions:
i) From the set of all agents, randomly select
without replacement an observer agent (O).
ii) O selects one actor agent (A), according to the
interaction probabilities that O has for the rest of the
agents.
iii) A behaves according to its concept with
probability equal to the value of the coefficient of
the concept that it has.
iv) O observes that behavior and modifies its
coefficient of the concept, according to the rules that
were previously described.
v) Repeat steps i) through iv) until all agents have
been observers.
We acknowledge that this description may not
provide the reader with a complete understanding of
our ABM. Space restrictions preclude providing
greater detail. In lieu, the ABM is available as a zip
file. The interested reader can download it from
http://www.uai.cl/images/stories/CentrosInvetigacio
AN ABM OF THE DEVELOPMENT OF SHARED MEANING IN A SOCIAL GROUP
7

n/CINCO/CAT_1_English.zip. To run it, you will
need first to install Netlogo version 4.0.4
(http://ccl.northwestern.edu/netlogo/). Once on the
ABM interface, do the following steps to run a
simulation: (1) Input the simulation parameters, be it
with the slider controls or typing the desired p(a1)
and p(a2) values in the appropriate windows. (2)
Press SETUP. (3) Press SIMULATE. (4) If you
want to pause a run, simply press SIMULATE (you
will need to press it again to resume).
4 PRELIMINARY RESULTS
Once the ABM was implemented and verified, we
carried out several runs to assess the dynamics of the
coefficients of the concepts that emerged. After
gaining some insights into the dynamics of those
coefficients and how different combination of
parameters changed those dynamics, we performed
experiments fixing the value of some parameters as
follows: number of agents = 100; number of
versions of a concept (or number of related
concepts) = 5; initial value of coefficients of
concepts = 0.5; and changing the value of p(a1) and
p(a2) between 0.1 and 0.95. According to the
combination of values for p(a1) and p(a2), three
different dynamics emerged.
4.1 Convergence to Zero
When we set small values for p(a1) and p(a2), for
example p(a1) = 0.1 and p(a2) = 0.2, then the
coefficients rapidly decrease and get close to zero,
remaining at that value. This can be seen in Figure 1,
where we plotted the mean value of the coefficient
of each version of the concept (c1 through c5) over
simulation steps. The mean value of each coefficient
is calculated by averaging the individual value of the
coefficient of the agents that have each version of
the concept.
Figure 1: Mean of coefficients of concepts (c1 through
c5), for p(a1) = 0.1 and p(a2)= 0.2.
That happens because the probability that O
observes a behaviour consistent with its concepts is
very low, since p(a1) and p(a2) are small. Thus, in
general, concepts tend to weaken, which in turn
makes it more probable that the coefficients will
keep decreasing throughout the run. Conceptually,
this is equivalent to concepts that are not useful to
generate agreement in a social group, and rapidly die
out.
4.2 Convergence to One
When both p(a1) and p(a2) are set to large values,
for example p(a1) = 0.8 and p(a2) = 0.9, then the
coefficients quickly increase and take values close to
1.0. This can be seen in Figure 2.
Figure 2: Mean of coefficients of concepts (c1 through
c5), for p(a1) = 0.8 and p(a2) = 0.9.
Contrary to what happened in 4.1, in this
situation p(a1) and p(a2) are large, thus favouring
that O observes a behaviour consistent with its
concepts, which will strengthen the coefficients. In
turn, this makes more probable that in successive
cycles, all the coefficients of the concepts will
increase. Conceptually, this is equivalent to a group
of related concepts synergistically increasing their
relevance by promoting agreement in culture.
4.3 Bifurcation
Using different combinations for p(a1) and p(a2),
such as (0.20, 0.80), (0.60, 0.40), (0.80, 0.16), we
saw that some concepts tended to strengthen and
others to weaken. We labelled this type of dynamic a
“bifurcation”, which is shown in Figure 3.
Under this condition, a relatively large value of
p(a1) or p(a2), but not of both of them, will promote
that on each run some Os observe behaviours
consistent with their concepts. However, since p(a1)
or p(a2) will have a small value, it will also happen
that on each run some Os will not observe
behaviours consistent with their concepts. Thus,
some versions of the concept will strengthen and
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
8
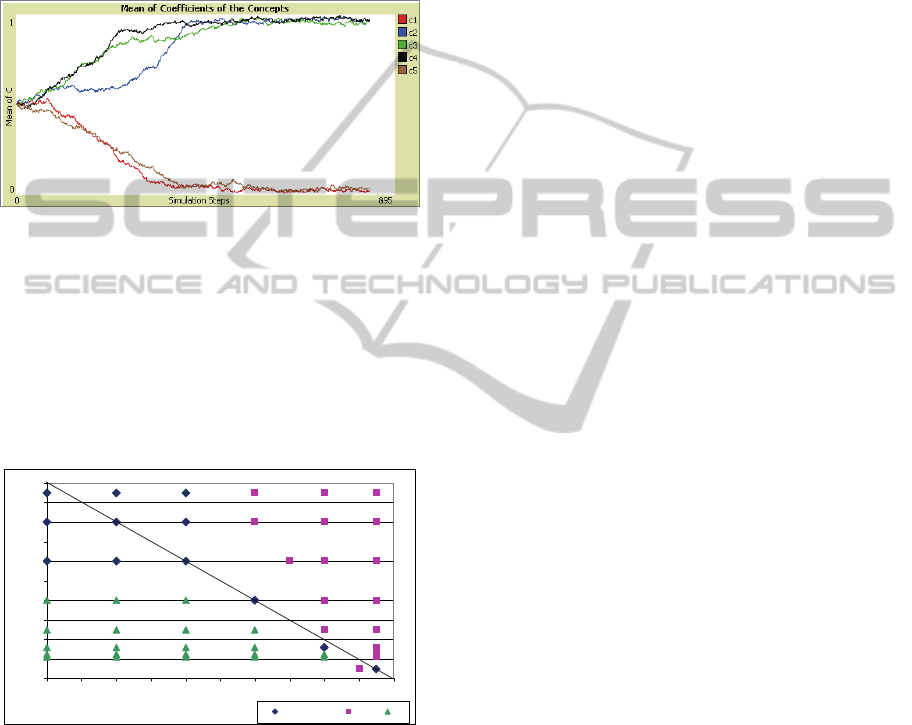
others weaken in agents’ minds. Conceptually, this
is equivalent to a group of related concepts that have
a weakly contrasting (i.e., somewhat overlapping)
conceptual alternative, such as might be the case of
concepts of male versus female gender, and concepts
of liberal versus conservative political views.
Concepts like these tend to become polarized in
large social groups, just as occurs in our model’s
bifurcations.
Figure 3: Mean of coefficients of concepts (c1 through
c5), for p(a1) = 0.2 and p(a2)= 0.8.
4.4 Map of Dynamics
Since we realized the significant influence of p(a1)
and p(a2) on the type of dynamics that emerged, we
ran simulations using more combinations for these
two variables. The types of dynamics of the
coefficients that emerged are presented in Figure 4.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
p(a1)
p(a2)
Bifurcation 1 0
Figure 4: Dynamics that emerge for coefficients of
concepts, according to values set to p(a1) and
p(a2)(bifurcation, 1 = convergence to 1, 0 = convergence
to 0).
We confirmed that for small values of p(a1) and
p(a2), we obtained convergence to zero; for large
values of p(a1) and p(a2), we saw convergence to
one; and for other combinations of those parameters,
we observed a bifurcation. Interestingly, note that
the combinations for p(a1) and p(a2), for which we
obtain a bifurcation, approximately lie on a line
connecting the lower right corner of the graph with
the upper left one. Moreover, see that the zone
where we get the bifurcation gets wider at the upper
left corner. That means that at the lower right corner
(p(a1) >> p(a2)), the dynamics of the ABM gets
more sensitive to the combination of p(a1) and p(a2)
than at the opposite corner (p(a1) << p(a2)). Since
that behaviour of the ABM was quite intriguing, we
developed another model to try to explain such
behaviour.
5 PROBABILISTIC
AND MARKOV CHAIN MODEL
To begin to validate the ABM results, and more
formally explain the conditions under which the
three dynamics appeared, we developed a simple
probabilistic model. This initial model justified why
the bifurcation emerged when the values for p(a1)
and p(a2) roughly lie on a line connecting the lower
right corner of the graph with the upper left one, as
shown in Figure 4.
5.1 Simple Conditional Probability
Model
To explain the three different types of dynamics that
emerge from the ABM, we use a simple conditional
probability model to calculate an initial probability
that a concept will strengthen (p
if
). If p
if
is small,
then most probably, the coefficient, which represents
the concept, will decrease. On the other hand, if p
if
is
large, the coefficient will increase. If p
if
is about 0.5,
then we obtain the ideal situation under which a
bifurcation might occur, i.e. each coefficient will
have a 50% chance of decreasing and a 50% chance
of increasing, thus making it possible that about half
of them will diminish and half of them will augment.
Figure 5 shows a conditional probability tree that
helps calculate p
if
.
In this model, p
if
depends on whether an agent A
(actor) behaves according to its concept (event BC),
which has probability equal to the initial value of the
coefficient that we set (c
0
), or not (event NBC, with
probability 1 - c
0
). Then, if A acts according to its
concept, then there is a p
i
probability that A and O
share all their conceptual content (event SACC), and
a 1- p
i
probability that they don’t share it all (i.e.,
each has a different version of the same concept,
event NSAAC). If they share all their conceptual
content (with probability pi), then it is certain that O
will strengthen its concept’s coefficient. If they
share versions of the same concept (with probability
AN ABM OF THE DEVELOPMENT OF SHARED MEANING IN A SOCIAL GROUP
9

1-p
i
), then it is less than certain (p(a1)) that O will
strengthen its concept.
Figure 5: Conditional probability tree for calculating p
if
.
On the other hand, if A does not behave
according to its concept (event NBC), and A and O
share all their conceptual content (event SAAC, with
probability p
i
), then O’s concept will certainly
weaken. Alternatively, if A and O do not share all
their conceptual content (event NSAAC), then it
might happen that A provides O with some portion
of the conceptual content, and thus O’s concept
might strengthen with probability p(a2).
Solving the probability tree of Figure 5 for p
if,
we
obtain:
pp
c
ppp
c
p
aiiaiif 2
0
1
0
)1)(1()]1([ −−+−+=
(1)
In (1), remember that p
i
corresponds to the
probability that agents share all their conceptual
content, i.e. that they have the same version of a
concept. Thus, we can calculate p
i
for the beginning
of a run. In such initial condition, we will have N/V
agents with the same version of a concept, where N
equals the total number of agents and V is the
number of different versions of a concept. Then, the
initial probability that agent O will interact with an
agent A that has the same version of the concept will
be equal to the number of other agents that have the
same version as O has (without counting O), divided
by the total number of agents (without counting O):
1
1
−
−
=
N
V
N
p
i
(2)
For the value of the parameters used in the runs, N =
100 and V = 5, so that p
i
= 19/99 = 0.1919.
Now, if we set p
if
= 0.5 in (1), i.e. the ideal
condition for obtaining a bifurcation, and establish
c
0
= 0.5 (the value we used in our simulation runs),
we can get equation (3), which states the ideal
condition for p(a1) and p(a2) for getting a
bifurcation.
0.1
21
=+
pp
aa
(3)
Note that (3) does not contain p
i
, which means
that that condition applies for any value of p
i
.
Equation (3) corresponds to a line with an intercept
with the y axis (p(a2) axis) equal to 1.0 and slope
equal to -1.0, which coincides with the line depicted
in Figure 4 that represents the combinations of p(a1)
and p(a2) where we obtained a bifurcation. Now, if
the sum of p(a1) and p(a2) is bigger than 1.0, we
obtain a parallel line to (3), but located above (3). In
that case, p
if
is larger than 0.5, and thus most
probably the coefficients will converge to one. This
coincides with the region of combinations for p(a1)
and p(a2), shown on Figure 4, where the coefficients
converge to one. To see that, we can rewrite (1),
replacing c
0
= 0.5:
p
pp
pp
i
iif
aa
−
−
=+
1
2
21
(4)
If we replace in (4) p
i
for its value 0.1919 and,
for example, set p
if
= 0.6, we obtain p(a1) + p(a2) =
1.248. On the other hand, if the sum of p(a1) and
p(a2) is smaller than 1.0, we also obtain a parallel
line to (3) but located below (3). In this case, p
if
will
be smaller than 0.5, and thus we will get a
convergence to zero of the coefficients. For
example, if we put p
if
= 0.4 in (4), we get the line
p(a1) + p(a2) = 0.753. That line is located within the
region of combinations of p(a1) and p(a2) shown in
Figure 4, where we obtain that dynamic.
However, from Figure 4, we can also see that on
the upper left corner of the graph, the line p(a1) +
p(a2) = 1.0 does not represent all the combinations
of p(a1) and p(a2) where the ABM exhibits the
bifurcation. Thus, the simple probability model only
partially explains the empirical results.
5.2 Markov Chain Model
Since the model in 5.1 calculates p
if
only for the
initial state of a simulation run, it cannot fully
capture the dynamical nature of the ABM.
Remember that the concepts’ coefficients change
during a run, as well as the interaction probabilities
among agents. In the ABM, that means that c
0
and p
i
p
if
BC: c
0
NBC: 1 – c
0
SAAC: p
i
NSAAC: 1 - p
i
1.0
p(a
1
)
p(a
2
)
0.0
SAAC: p
i
NSAAC: 1 - p
i
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
10

will change as the simulation run advances. Thus,
we need to build a model that captures that
dynamical aspect of the ABM. To do so, we use a
simple Markov chain, with four states, as described
in Table 1.
Table 1: State transition probability matrix of the Markov
chain.
S
t+1
(
j
= 0) W
t+1
(
j
= 1)
S
t
(i = 0) p
i
f
+
1 - p
i
f
+
W
t
(i = 1) p
i
f
-
1- p
i
f
-
Table 1 indicates that if a concept strengthens
(state S
t
(i = 0)), then the probability that it will
increase in the next step (state S
t+1
(j = 0))
is p
if
+
, and
that it will weaken is 1 - p
if
+
(state W
t+1
(j = 1)). On
the other hand, if a concept weakens (state W
t
(i =
1)), then the probability that it will strengthen in the
next step (state S
t+1
(j = 0)) is p
if
-
and that it will
weaken (state W
t+1
(j = 1)) is 1- p
if
-
. In the ABM,
each of those p
if
has a meaning. From expression (1),
we know that p
if
depends on c and p
i
, which change
during a simulation run. The description of the ABM
states that if a concept strengthens, then its
coefficient will increase by a certain
Δ
c, and the
same will happen with p
i
, which will increase by
Δ
p
i
. If the concept weakens, then the coefficient c
will decrease by
Δ
c, but p
i
will remain the same.
Therefore, using those facts, we can write the
following expressions for p
if
+
and p
if
-
:
0
(, ) ,
if i i i i
if
with c
p
pppp
ccc
p
++
++
+
=+Δ = +Δ=
(5)
0
(, ) ,
if if i i i
w ith c
pp p pp
ccc
−− −
−−
==−Δ=
(6)
Then, replacing (5) and (6) in (1), we can write the
explicit equations for p
if
+
and p
if
-
:
01
0
2
)[( ) (1 )]
(1 )(1 )
(
if i i a i i
iia
c
c
p
cppppp
ppp
c
+
=+Δ +Δ+ −−Δ
+− −Δ − −Δ
(7)
01
0
2
)[ (1 )]
(1 ) (1 )
(
if i a i
ia
c
c
pc pp p
pp
c
−
=−Δ + −
+− +Δ −
(8)
Now, if we apply the properties of an ergodic
Markov chain (c.f. Ross, 1998), we can compute a
long-run probability that a concept will strengthen
(
Π
0
):
pp
p
ifif
if
+−
−
−+
=
Π
1
0
(9)
Since (9) is written in terms of p
if
+
and p
if
-
, which
in turn are given by (7) and (8), it would be rather
cumbersome to write an explicit equation for (9) in
terms of c,
Δ
c, p
i
,
Δ
p
i
,
p(a
1
) and p(a
2
). Thus, we
prefer to use the following definitions and write a
simpler expression for
Π
0
:
00
00
00
() ()( )
()(1) ()( )
(1 )(1 ) (1 )( )
1
1
iii
iii
iii
ac ec
bc f c
dc gc
ppp
cc
ppp
cc
ppp
cc
=−Δ =+Δ +Δ
=−Δ− =+Δ −Δ
=− +Δ − =− −Δ −Δ
−
−
(10)
Then, using (10), we can write:
12
0
12 12
1
aa
aa aa
ab d
ab d e f g
pp
p
ppp
++
=
++ + −− −
Π
(11)
Expression (11) can be rearranged so that it looks
similar to equation (4), i.e. represents a line that
states the relationship that must exist between p(a1)
and p(a2) for a given
Π
0
:
00 000
21
00 00
aa
bfb a ae
dgd dgd
pp
+− +−+
=+
−− −−
ΠΠ ΠΠΠ
ΠΠ ΠΠ
(12)
Note that (12) is an equation of a line with a slope
equal to the expression located to the left of p(a1)
and an intercept with the y axis (p(a2) axis) equal to
the far right hand expression. If we compare (12)
with (4), we can see that the slope in (4) does not
change, depending on the values that p(a1), p(a2)
and p
if
take; but in (12) the slope changes (remember
that p
if
in (4) is equivalent to
Π
0
in (12)). Moreover,
if we set in (10), c
0
= 0.5, p
i
= 0.1919,
Δ
c = 0.45 and
Δ
p
i
= 0.05; and put the values a through g, defined
in (10), in (12), we can get a family of lines that
represents the condition that must meet p(a1) and
p(a2) for obtaining different values of
Π
0
. Figure 6
shows the same graph presented in Figure 4, but
displaying lines for
Π
0
= 0.3 to 0.7 according to the
Markov chain model that corresponds to expression
(12).
From Figure 6, we can see that the line for
Π
0
=
0.5 (the ideal condition for getting a bifurcation)
approximately coincides with a line equal to the one
we calculated for the simple probabilistic model (see
expression (3) and Figure 4). The other lines for
Π
0
= 0.6 and 0.7 are located in the region where the
ABM exhibits the convergence to one dynamic and
the lines for
Π
0
= 0.3 and 0.4 lie in the region where
the convergence to zero dynamic emerges. Thus, we
can see that the Markov chain model represents
fairly well the conditions under which the ABM
AN ABM OF THE DEVELOPMENT OF SHARED MEANING IN A SOCIAL GROUP
11
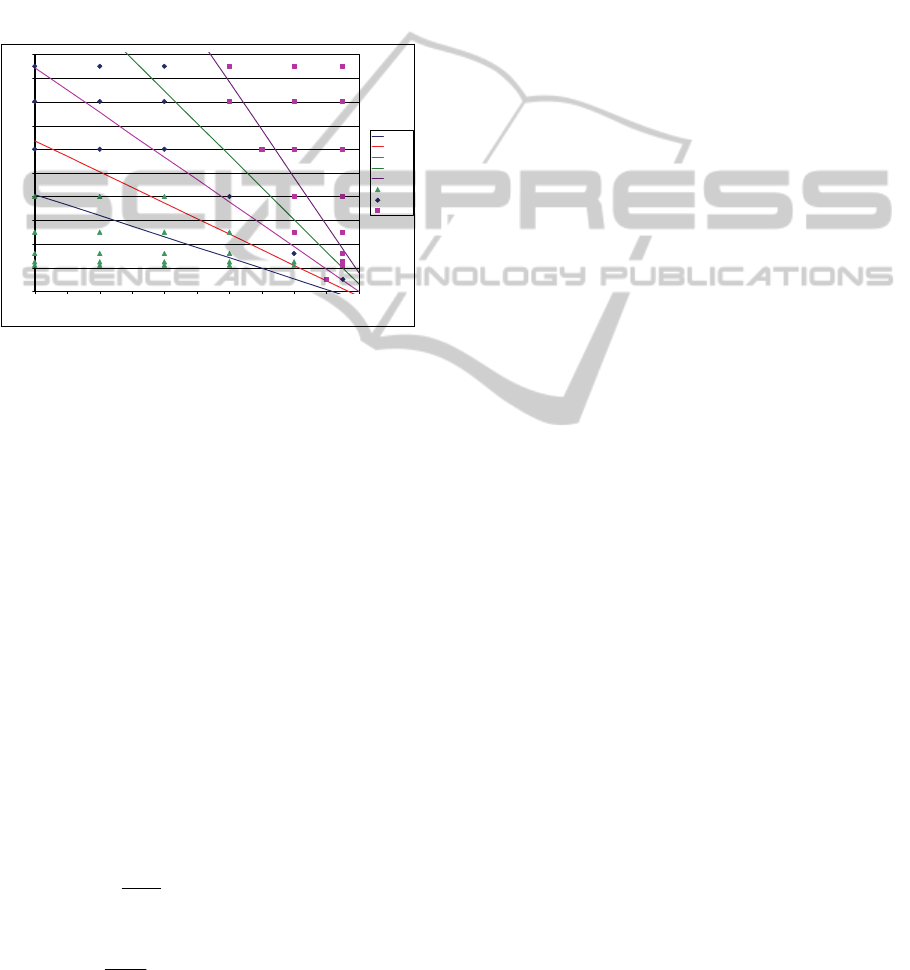
exhibits the three different dynamics. Moreover,
note that the lines tend to converge toward the lower
right corner of the graph, where p(a1) >> p(a2) and
tend to diverge toward the upper left corner, where
p(a1) << p(a2). This means, that the region where
we get the bifurcation and which separates the areas
where we obtain the convergence to one and zero,
gets narrower when p(a1) >> p(a2) and wider when
p(a1) << p(a2). That characteristic was the one that
the probabilistic model described in 5.1 was not able
to capture.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
pa1
pa2
Πο = 0.3
Πο = 0.4
Πο = 0.5
Πο = 0.6
Πο = 0.7
0
Bif
1
Figure 6: Dynamics that emerge for coefficients of
concepts, according to values set to p(a1) and
p(a2)(bifurcation, 1 = convergence to 1, 0 = convergence
to 0) and lines for different values of Π
0
according to the
Markov chain model.
5.3 Sensitivity of Models to Changes in
Values of some Parameters
By analyzing the ABM’s and its associated
probabilistic models’ sensitivity to different
parameters, we are able to derive predictions for
“real world” situations. Although the Markov chain
model presented in 5.2 better explains the dynamical
properties of the ABM than the probabilistic model
described in 5.1, the latter model is easier to analyze
from a substantive point of view. Thus, based on
expression (1), we will compute the sensitivity of
that model to changes in values of some parameters.
Here, we will present only two results of such
analyses. To do so, we use (1) and take the partial
derivatives of p
if
with respect to p(a1) and p(a2):
)1(
0
1
p
c
p
p
i
a
if
−=
∂
∂
(13)
)1)(1(
0
2
p
c
p
p
i
a
if
−−=
∂
∂
(14)
Additionally, since p
i
appears in (13) and (14)
and that variable depends on the number of agents
and concepts (N, V see (2)), we can express (13) and
(14) in terms of N and V. Moreover, given that for
reasonably large values of N, p
i
tends to 1/V, we will
analyze (13) and (14) taking into consideration that
p
i
≈1/V.
From (13) and (14) we can see that the
sensitivity of p
if
with respect to p(a1) and p(a2) is
always positive (remember that 0 ≤ c
0
, p
i
≤ 1), i.e.
the larger p(a1) and p(a2), the larger p
if
. Now, the
larger the number of concepts a group has (V), the
smaller p
i
will be and the more influential p(a1) and
p(a2) will be on the value that takes p
if
. That means
that for groups with a large set of related concepts
(or many different versions of the same concept), the
probability of true and illusory agreement (p(a1) and
p(a2)) will greatly influence p
if
. The significance of
that influence will also be determined by the value
of c
0
. Note that for large values of c
0
, p(a1) will have
a larger influence on p
if
than p(a2) and vice-versa.
Thus, for groups with many concepts, the degree of
agreement, either true or illusory, and the initial
strength of each concept will dictate whether each
concept strengthens or weakens, and eventually
disappears.
Several “real world” situations could conform to
the dynamics described above. As an illustration,
imagine a social group that has an abstract concept,
such as conservative. Presumably, people would
have many different versions of such concept (i.e., a
small p
i
), with some people, e.g., considering that
conservative is a view about economics, while
others considering that it is a view about values, and
so on. Imagine, furthermore, that this concept’s
relevance in that society is moderate, in the sense
that it does not persistently determine people’s
actions (i.e., c
0
≠ 1). For concepts like this, our
sensitivity analyses predict that their fate as a
cultural phenomenon will depend mainly on their
capacity to generate agreement.
Imagine, furthermore, that conservative has
liberal as a weakly contrasting alternative concept
(liberal is weakly contrasting to conservative
because it does not clearly divide political opinion in
two sharply contrasting clusters). Our sensitivity
analyses predict that the fate of this pair will depend
on agreement, regardless of whether it is true (p(a1))
or illusory (p(a2)). Additionally, as discussed in 4.3
above, these conditions promote bifurcations akin to
social polarization.
Perhaps, an even more interesting situation arises
in groups that have a small number of concepts or
versions of them. In that case, p
i
will be large, and
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
12

thus p(a1) and p(a2) will not have a large influence
on p
if
(i.e., the degree of true and illusory agreement
will not have a large influence on the fate of the
concepts). Examining Figure 5, we can see that in
the above mentioned situation, the fate of each
concept will be predominantly dictated by its initial
strength c
0
, i.e., an initially rather strong concept
will disseminate throughout the group and become
stronger, and an initially quite weak concept will die
out. Note that since in this situation, agreement of
any type is almost irrelevant, that implies that a
concept may spread even if people do not share the
same meaning of it.
Again, a “real world” situation that could
conform to these conditions is the following.
Imagine a social group in which an authority (moral,
political, or other) pushes an oversimplified concept
(e.g., a slogan), and creates the conditions to make it
relevant (e.g., punishes dissent). As occurs with
commands, slogans may leave little room for
alternative interpretations (i.e., p
i
is large), which, by
equations (13) and (14) implies that agreement
ceases to be the predominant force that drives that
concept’s path. In other words, if an authority
presents a very simple idea that allows little room
for alternative interpretations, and succeeds in
making it relevant in people’s minds (i.e., makes c
0
sufficiently large), that condition will be sufficient to
strengthen the concept and disseminate it throughout
the social group, regardless of whether its meaning
is shared or not.
6 CONCLUSIONS
In the work we report here, we use our ABM to
develop a complex theory about the dynamics of
shared meaning in social groups. This use of ABMs
is not new, and has been advocated by Ilgen and
Hulin (2000). Our ABM embodies some very simple
rules of interaction, in keeping with Axelrod’s
(1997) KISS principle. However, the ABM’s
dynamics are not simple, as attested by the expanded
region of combinations of p(a1) and p(a2) in Figure
4, where bifurcations emerge.
Our theory development approach to Agent
Based Modeling led us to formalize the dynamics
through increasingly refined probabilistic models.
Not only is this currently allowing us to recursively
improve our ABM, but it also allowed us to clearly
link the conceptual and mathematical formulations
of our theory (respectively, sections 1 and 2, and
section 5), and to gain a more general and clear
understanding of the ABM’s dynamics.
It is true that our model is, at this point, purely
theoretical, and that it requires data to support it.
However, we incorporated into the ABM generally
accepted psychological theory, and as our sensitivity
analyses in 5.3 show, the ABM makes intuitively
correct predictions that were not built into it in an ad
hoc fashion. These two aspects, we think, are at least
evidence of the ABM’s face validity. We would be
very disappointed if future work shows that this
validity is only illusory.
REFERENCES
Axelrod, R. (1997). Advancing the Art of Simulation in
the Social Sciences. in Simulating Social Phenomena.
Rosario Conte, Rainer Hegselmann and Pietro Terna
Eds. Berlin: Springer-Verlag.
Brennan, S. E. & Clark, H. H. (1996). Conceptual pacts
and lexical choice in conversation. Journal of
Experimental Psychology: Learning, Memory, and
Cognition, 22, 1482–1493.
Brewer, M. B. (1988). A dual process model of impression
formation. In T. K. Srull and R. S. Wyer Jr. (Eds.),
Advances in Social Cognition (pp. 1–36), Hillsdale,
NJ: Erlbaum.
Brown-Schmidt, S. & Tanenhaus, M. K. (2008). Real-time
investigation of referential domains in unscripted
conversation: A targeted language game approach.
Cognitive Science, 32, 643–684.
Carpenter, M., Nagell, K. & Tomasello, M. (1998). Social
cognition, joint attention, and communicative
competence from 9 to 15 months of age. Monographs
of the Society for Research in Child Development,
63(4), 1-143.
Chaigneau, S. E. & Gaete, J. (2010). Agreement in
Conventionalized Contexts. Manuscript presented for
publication.
Clark, H. H. & Krych, M. A. (2004). Speaking while
monitoring addressees for understanding. Journal of
Memory and Language, 50(1), 62-81.
Evans, J. St. B. T. (2008). Dual-processing accounts of
reasoning, judgment, and social cognition. Annual
Review of Psychology, 59, 255-278.
Galantucci, B. & Sebanz, N. (2009). Joint action: current
perspectives. Topics in Cognitive Science, 1, 255-259.
Garrod, S., & Anderson, A. (1987). Saying what you mean
in dialogue: A study in conceptual co-ordination.
Cognition, 27, 181–218.
Ilgen, D. R. & Hulin, Ch. L. (2000). Computational
modeling of behavior in organizations. Washington
D.C.: American Psychological Association.
Lenton, A. P., Blair, I. V., & Hastie, R. (2001). Illusions of
gender: Stereotypes evoke false memories. Journal of
Experimental Social Psychology, 37(1), 3-14.
Lewis, D. (1969). Convention: A Philosophical Study.
Cambridge: Harvard University Press.
AN ABM OF THE DEVELOPMENT OF SHARED MEANING IN A SOCIAL GROUP
13

Lewis, D. (1975). Languages and Language. In Keith
Gunderson (Ed.), Minnesota Studies in the Philosophy
of Science, Volume VII (pp. 3–35). Minneapolis:
University of Minnesota Press.
Millikan, R. G. (2005). Language: A biological model.
Oxford: Oxford University Press.
Moses, L. J., Baldwin, D. A., Rosicky, J. G. & Tidball, G.
(2001). Evidence of referential understanding in the
emotions domain at 12 and 18 months. Child
Development, 72, 718–735.
Nickerson, R. (1998). Confirmation bias: A ubiquitous
phenomenon in many guises. Review of General
Psychology, 2, 175–220.
Richardson, D. C., Dale, R. & Tomlinson, J. M. (2009).
Conversation, gaze coordination, and beliefs about
visual context. Cognitive Science, 33, 1468-1482.
Rosch, E. & Mervis, C. B. (1975). Family resemblances:
Studies in the internal structure of categories.
Cognitive Psychology, 7, 573-605.
Ross, S. M. (1998). A First Course in Probability (5th
ed.). New Jersey: Prentice Hall.
Rudman, L. A. & Phelan, J. E. (2008), Backlash effects
for disconfirming gender stereotypes in organizations.
Research in Organizational Behavior, 28, 61-79.
Tomasello, M. (1995). Joint attention as social cognition.
In C. Moore & P. J. Dunham (Eds.), Joint attention:
its origins and role in development (pp. 103-130).
Hillsdale, NJ: Lawrence Erlbaum.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
14
