
A MULTIOBJECTIVE CONSTRAINT OPTIMIZATION MODEL FOR
MULTIMODE REPAIR PLANS
I. Barba, C. Del Valle and D. Borrego
Dpto. Lenguajes y Sistemas Inform´aticos, Universidad de Sevilla, Spain
Keywords:
Planning, Scheduling, Constraints, Repair, Multiobjective optimization, Multimode project scheduling.
Abstract:
This work presents a constraint based model for the planning and scheduling of disconnection and connection
tasks when repairing faulty parts. The problem involves the ordering and the selection of tasks from a set of
alternatives. The goal of the plan is the minimization of the repair duration and cost. The model considers,
apart from the durations, costs and resources for the tasks, the necessary delays and costs due to auxiliary tasks.
The tasks can be executed in several operating modes, each one using a different machine or configuration and
possibly different duration and cost. The set of all feasible plans are represented by an extended And/Or graph.
1 INTRODUCTION
There is an increasing interest for integrating plan-
ning and scheduling since real-world problems in-
volve both of them (Boddy et al., 2004). Some of the
applications involving such issues are maintenance
and repair planning, where there may be a cascad-
ing set of choices which affect different features of
the plan, such as duration or cost (Smith et al., 2000).
Many problems can involve multiple conflicting ob-
jectives (Deb, 2008) that should be considered at the
same time.
This work presents a CSP (Constraint Satisfaction
Problem) model for solving a planning problem corre-
sponding to the optimal sequencing of disconnection
and connection tasks for repairing faulty components.
The objective is the minimization of the total repair
time and cost, considering different factors that can
have an influence on it. The tasks can be executed in
several operating modes (Kolisch and Drexl, 1999),
each one using a different machine or configuration,
and possibly different duration and cost.
The rest of the paper is organized as follows: Sec-
tion 2 details the considered repair problem, Section
3 states the CSP model for planning the reparation
of faulty components and, finally, Section 4 presents
some conclusions and future work.
2 REPAIR PLANNING
In order to repair a faulty part, a sequence of discon-
nection tasks must be executed to get it, then a repair
action would repair the component, and lastly some
connection tasks must reconnect the system.
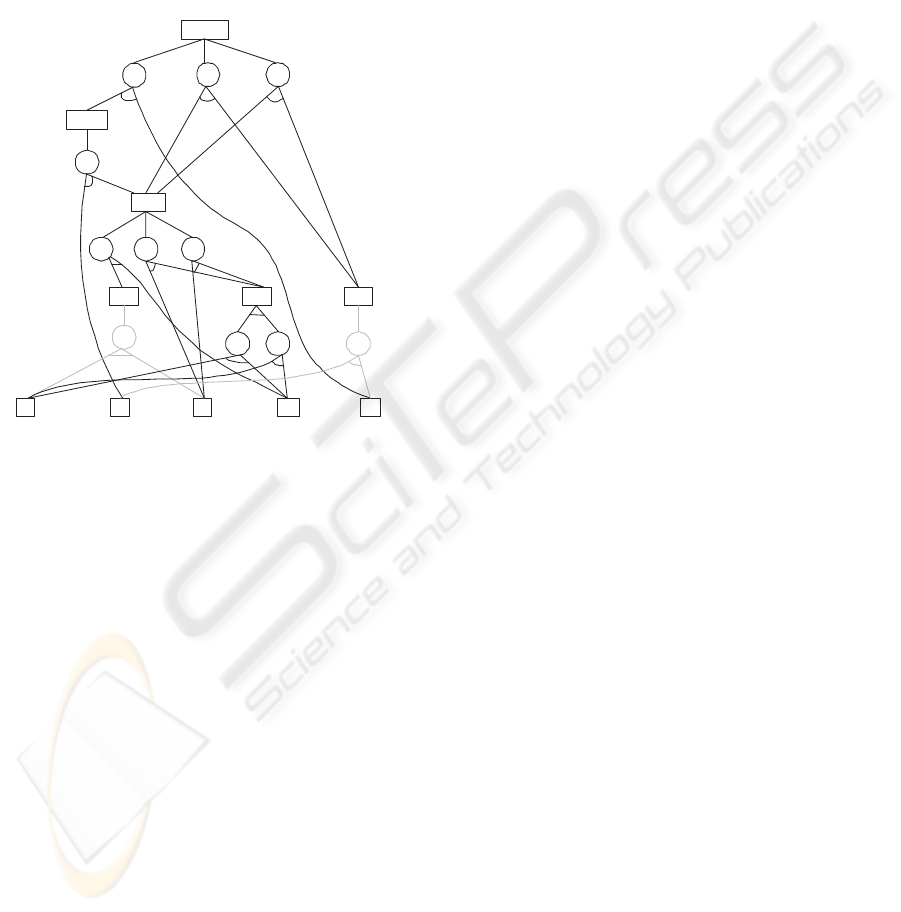
The use of And/Or graphs (Homem de Mello and
Sanderson, 1990) allows to represent the set of all fea-
sible plans in a natural way. An important advantage
of And/Or graph is that it shows the tasks that can
be executed in parallel (Fig. 1). Furthermore, both
precedence constraints and those related to the selec-
tion of tasks for obtaining a correct plan, can be easily
obtained from this representation.
A feasible repair plan can be seen as a set of
tasks that have to be executed, containing: Connec-
tion/Disconnection tasks, that are executed on an es-
tablished machine with a particular configuration and
Auxiliary tasks (set-up operations, that change the
configuration of a machine when two successive tasks
with different configuration use it; and transportation
operations, that transport the subsystems between ma-
chines when the machine where the subsystem is ob-
tained is different from the one where is required).
The tasks can be executed in more than one op-
erating mode, each one using a different machine or
configuration and possibly different duration and cost,
and will be represented by differentAnd nodes (i.e. T
′
2
and T
′
3
in Fig. 1).
A repair graph is a subgraph of the And/Or graph
which only contains the tasks that could be necessary
to repair some components. Another important con-
sideration is that a connection (disconnection) task T
is reversible if its corresponding disconnection (con-
nection) task T
′
is feasible. The model supposes two
355
Barba I., Del Valle C. and Borrego D. (2009).
A MULTIOBJECTIVE CONSTRAINT OPTIMIZATION MODEL FOR MULTIMODE REPAIR PLANS.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,
pages 355-358
DOI: 10.5220/0002192003550358
Copyright
c
SciTePress
assumptions: (A1) All tasks are reversible and (A2)
Subsystems that do not include the faulty components
are not disconnected. Taking into account this, other
subsystems different from the ones generated by the
disconnection process can appear in the connection
process. Moreover, disconnection tasks only handle
subsystems that contain the faulty component. Al-
though the disconnection process is linear, the con-
nection can contain tasks that may execute in parallel
with others.
ABCDE
ABCD
ACD
AC
A
AD BE
B C D E
T’
3
T’
2
T’
1
T’
7
T’
9
T’
4
T’
5
T’
6
T’
10
T’
8
T’
11
Figure 1: A simplified disconnection And/Or graph.
3 THE CSP MODEL
Constraint Programming (CP) has been evolved in the
last decade to a mature field because, among others,
of the use of different generic and interchangeable
procedures for inference and search, which can be
used for solving different types of problems (Rossi
et al., 2006). Once a problem is modelled by a CSP, a
generic or specialized CSP solver can be used in order
to obtain the required solution.
Taking into account (A1) and (A2), the graph can
be simplified removing those And nodes below the
Or nodes corresponding to subsystems which do not
contain the faulty part (Fig. 2).
3.1 Variables of the CSP
Selection Variables. For each And node, two boolean
variables represent if the connection s(T) and discon-
nection tasks s(T
′
) are selected for the solution. Fur-
thermore, for each Or node, two boolean variables
represent if the subsystem S appears in the connection
s(S) and disconnection processes s
′
(S).
Resource Variables. For each And node, M(T) and
M(T
′
) represent the machines used, and C f(T) and
Cf(T
′
) are the necessary configuration on them for
the connection and disconnection tasks respectively.
On the other hand, the machine where a subsys-
tem is obtained after the corresponding disconnection
and connection task, are represented by the variables
m
′
(S) and m(S).
Time Variables. For each And node, the durations of
the associated tasks Dur(T) and Dur(T
′
) are estab-
lished. For the auxiliary operations, ∆
cht
(M, Cf, C f
′
)
denotes the time needed for changing the config-
uration of the machine M from Cf to C f
′
, and
∆
mov
(S, M, M
′
) denotes the time needed for transport-
ing the subsystem S from machine M to machine M
′
.
Finally, a temporal delay ∆
subst
(C) is associated to
the reparation of the faulty component. On the other
hand, for each And node: its starting and ending
times, t
i
(T) and t
i
(T
′
), t
f
(T) and t
f
(T
′
). For each Or
node, the times when it is obtained after connection,
t
OR
(S), and disconnection, t
′
OR
(S).
Cost Variables. For each And node: its connection
Cost(T
i
) and disconnection cost Cost(T
′
i
). Regard-
ing to the auxiliary operations, Cost
cht
(M, Cf, C f
′
)
denotes the cost of changing the configuration of the
machine M fromCf toCf
′
, andCost
mov
(S, M, M
′
) de-
notes the cost of transporting the subsystem S from
machine M to machine M
′
. Furthermore, a cost
Cost
subst
(C) is associated to the reparation of the
faulty component. On the other hand, for each And
node, the selection of the corresponding task T may
be associated some additional costs: first, the variable
cost
mov
(T
i
) represents the possible costs associated to
the movement of subsystems; and secondly, the vari-
able cost
cht
(T
i
) represents the possible costs of change
of configuration.
The original And/Or graph has been extended,
adding new types of links between And nodes. The
new links represent non-precedence constraints: due
to the use of shared resources by the tasks and due to
the change of configurations in the machines.
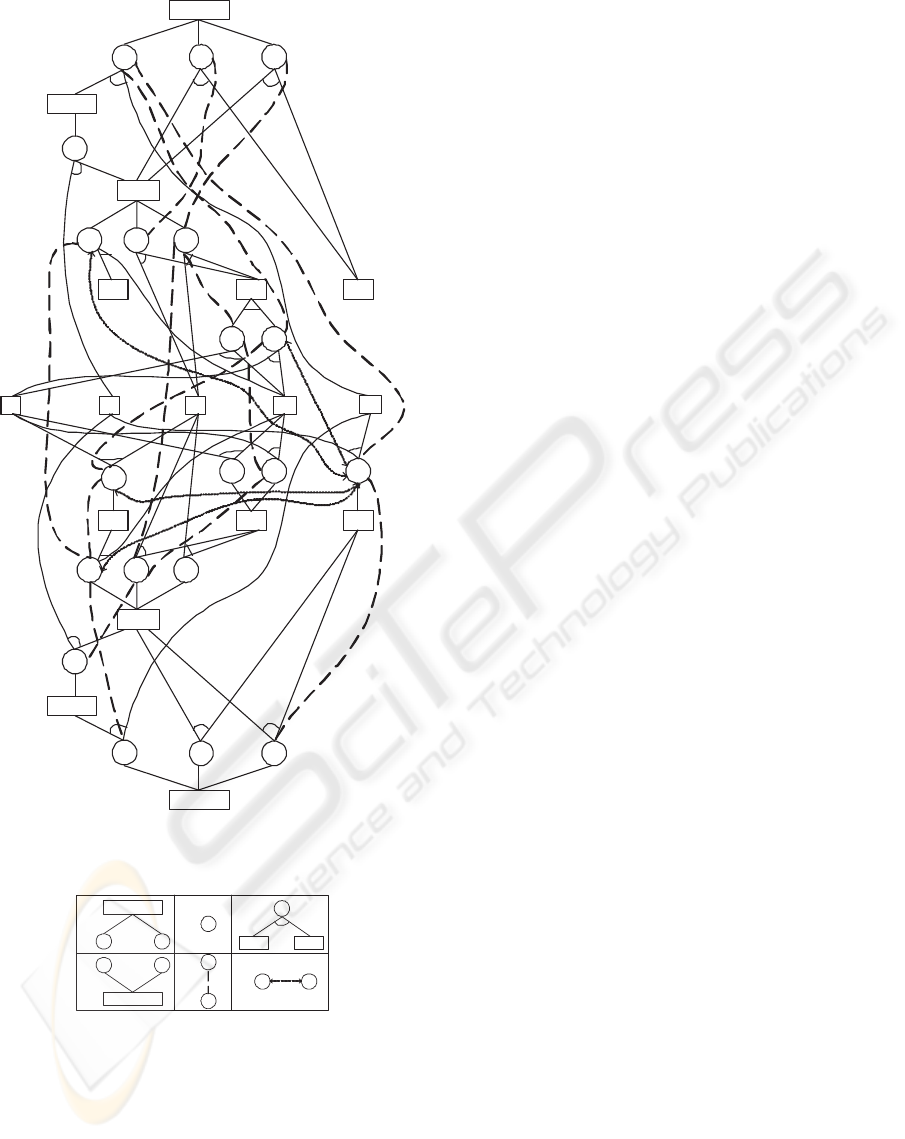
Fig. 2 shows the extended and simplified re-
pair And/Or graph of a system consisting in ABCDE
components when substituting D. A typical objec-
tive for such a problem would be the minimization
of the elapsed time of the plan, given by the variable
(t
OR
(ABCDE)). Another important issue is the total
cost of the complete repair plan. In this work, a multi-
objective optimization is pursued, encompassing both
of them.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
356
ABCDE
ABCD
ACD
AC
A
AD BE
B C D
T’
3
T’
2
T’
1
T’
7
T’
9
T’
4
T’
5
T’
6
T’
10
ABCDE
ABCD
ACD
AC AD BE
E
T
3
T
2
T
1
T
7
T
9
T
4
T
5
T
6
T
10
T
8
T
11
M
2
C
3
M
1
C
1
M
3
C
4
M
1
C
2
M
2
C
3
M
1
C
2
M
3
C
2
M
3
C
6
M
2
C
1
M
2
C
4
M
1
C
2
M
2
C
4
M
3
C
3
M
2
C
5
M
1
C
2
M
3
C
2
M
3
C
6
M
2
C
4
M
2
C
5
M
1
C
2
Figure 2: The simplified repair And/Or graph with relations
(5) and (6) between tasks
...
...
(1) (2) (3)
(4) (5) (6)
Figure 3: Types of Relations
3.2 Types of Constraints
Six types of relations are considered (Fig. 3), each
one representing a link or component of the extended
graph (Fig. 2): Relations of type (1) collect the rela-
tion between the information from an Or node and the
And nodes below it. Relations of type (2) consider the
durations of tasks, and correspond to the relations be-
tween its starting and ending times. Relations of type
(3) collect the relation between the information from
an And node and the Or nodes below it. Relations of
type (4) consider the relation between the selection of
an Or node and all the And nodes above it. Relations
of type (5) are due to the delay needed for a change
of configuration in a machine between the executions
of two successive tasks using the same machine with
precedence constraints among them. Relations of type
(6) consider the relation between some tasks that use
the same resource. Types (1), (2), (3) and (4) come
from the relations between the nodes included in the
original And/Or graph, while types (5) and (6) come
from the use of (same or different) resources by the
different tasks, and they are related to new links be-
tween tasks in the extended And/Or graph.
Taking into account the variables of the proposed
model, selection, resource, time and cost constraints
are considered. A previous work (Del Valle et al.,
2009) includes the first three kinds of constraints.
Selection Constraints. Collect the relations between
the boolean variables that represent if the tasks are
selected for the solution and the subsystems appears
in the repair process. A special case is for the com-
plete system and for the faulty component, which al-
ways will be part of the solution. The constraints
of type (1) include the selection of disconnection
tasks T
′
and connection tasks T with that of sub-
systems: s
′
(S) ⇔ XOR
T
′
i
∈succ(S)
(s(T
′
i
)) and s(S) ⇔
XOR
T
i
∈succ(S)
(s(T
i
)). Related to relations of type
(3), the selection of the two Or nodes if the And
node is selected: s(T
′
) ⇒ s
′
(S
1
) ∧ s
′
(S
2
) and s(T) ⇒
s(S
1
) ∧ s(S
2
). The constraints of type (4) include
the selection of tasks T
′
and T with that of sub-
systems: s
′
(S) ⇔ XOR
T
′
i
∈pred(S)
(s(T
′
i
)) and s(S) ⇔
XOR
T
i
∈pred(S)
(s(T
i
)).
Resource Constraints. Consider the relations be-
tween the machines used in the tasks, and those where
the subsystems are obtained after them. Related to re-
lations (1), the machine m where a subsystem is gen-
erated after a connection task is the machine used by
this task: s(T
i
) ⇒ m(S) = M(T
i
). Related to relations
of type (3), the machine m
′
where a subsystem is gen-
erated after a disconnection task is the machine used
by this task: s(T
′
i
) ⇒ m
′
(S
1
) = m
′
(S
2
) = M(T
′
i
).
Time Constraints. Time constraints collect the rela-
tions between the start and the end times of the tasks,
and the time when the subsystems are obtained. Re-
lated to relations of type (1), these constraints estab-
lish the disconnection t
′
OR
and connection times t
OR
of Or nodes related to the start times of the discon-
A MULTIOBJECTIVE CONSTRAINT OPTIMIZATION MODEL FOR MULTIMODE REPAIR PLANS
357

nection tasks or the end times of the connection tasks:
s(T
′
i
) ⇒ t
i
(T
′
i
) ≥ t
′
OR
(S) + ∆
mov
(S, m
′
(S), M(T
′
i
)) and
s(T
i
) ⇒ t
f
(T
i
) = t
OR
(S). Related to relations of type
(2), these constraints consider the end time of the
tasks related to the start time and the durations of
them: s(T
′
i
) ⇒ t
f
(T
′
i
) = t
i
(T
′
i
)+ Dur(T
′
i
) and s(T
i
) ⇒
t
f
(T
i
) = t
i
(T
i
) + Dur(T
i
). Related to relations (3), the
next constraints include the equality constraint be-
tween the disconnection times of the Or nodes t
′
OR
and the end time of a disconnection task T
′
above
them: s(T
′
i
) ⇒ t
f
(T
′
i
) = t
′
OR
(S
1
) = t
′
OR
(S
2
), and the
precedence between the connection time of the Or
nodes t
OR
and the start times of connection task T,
and considering the possible delays due to the trans-
portation of subsystems if the two successive tasks
involving it use different machines: s(T
i
) ⇒ t
i
(T
i
) ≥
t
OR
(S
1
)+ ∆
mov
(S
1
, m(S
1
), M(T
i
)) and s(T
i
) ⇒ t
i
(T
i
) ≥
t
OR
(S
2
) + ∆
mov
(S
2
, m(S
2
), M(T
i
)). Related to rela-
tions of type (5), these constraints establish that for
a task T
i
, and its closest predecessor task T
j
us-
ing the same machine m, taking into account the
possible change of configuration: (s(T
i
) ∧ s(T
j
)) ⇒
t
i
(T
j
) ≥ t
f
(T
i
) + ∆
cht
(m, Cf(T
i
), Cf(T
j
)). For each
two tasks T
i
and T
j
requiring the same machine
m, with no precedence constraint among them, and
which may belong to the same repair plan, the con-
straints of type (6) express the two possible orders
of execution of the tasks: (s(T
i
) ∧ s(T
j
)) ⇒ (t
i
(T
i
) ≥
t
f
(T
j
) + ∆
cht
(m, Cf(T
j
), Cf(T
i
)) ∨ t
i
(T
j
) ≥ t
f
(T
i
) +
∆
cht
(m, Cf(T
i
), Cf(T
j
))). For the Or leaf nodes t
′
OR
and t
OR
are equals, except for the faulty component
due to the delay corresponding to the reparation.
Cost Constraints. The cost of a plan can be estab-
lished by the aggregated costs associated to the exe-
cution of the selected tasks. The total cost of selecting
a task T
i
involves:
• the execution cost of the task, Cost(T
i
)
• the cost associated to the possible machine move-
ment of one or two subsystems, cost
mov
(T
i
):
first, in disconnection tasks T
′
i
, the possi-
ble movement of the subsystem related to
the Or nodes above it, related to relation
(1), cost
mov
(T
′
i
) = Cost
mov
(S, m
′
(S), M(T
′
i
)); sec-
ondly, in connection tasks T
i
, the possi-
ble movement of the two subsystems related
to Or nodes below it, related to relation
(3), cost
mov
(T
i
) = Cost
mov
(S
1
, m(S
1
), M(T
i
)) +
Cost
mov
(S
2
, m(S
2
), M(T
i
)).
• the possible cost associated to a change of config-
uration on M(T
i
), cost
cht
(T
i
). If M(T
i
) has been
used before by another task with a different con-
figuration, it is necessary to change it. The cost
of the change of configuration depends of the se-
quence of tasks for each machine, so there must be
considered the precedent task executed on m(T
i
).
Taking into account this, cost
cht
(T
i
) =
Cost
cht
(M(T
i
), Cf(PM(T
i
)), Cf(T
i
)), where
PM(T
i
) is the precedent task executed on m(T
i
).
Also, the total cost of a plan can be defined as
∑
T
i
s(T
i
)(Cost(T
i
) + cost
mov
(T
i
) + cost
cht
(T
i
)).
4 CONCLUSIONS AND FUTURE
WORK
This work proposes a CSP model for the planning and
optimal sequencing of disconnection and connection
multi-mode tasks when repairing faulty components,
taking into account the minimization of time and cost.
The proposed model can be solved using conventional
methods for a generic CSP. As future work, it is in-
tended to use different strategies to solve the problem,
working with heuristic algorithms based on the result-
ing state of the constraint propagation process and on
the objective functions to be optimized.
ACKNOWLEDGEMENTS
This work has been partially supported by the Span-
ish Ministerio de Educaci´on y Ciencia through a coor-
dinated research project (Grant DIP2006-15476-C02-
01) and Feder (ERDF).
REFERENCES
Boddy, M., Cesta, A., and Smith, S. (2004). ICAPS-04 Ws.
Integrating Planning into Scheduling. AAAI Press.
Deb, K. (2008). Introduction to evolutionary multiobjec-
tive optimization. Lecture Notes in Computer Science
5252 LNCS, pages 59–96.
Del Valle, C., M´arquez, A., and Barba, I. (2009). A csp
model for simple non-reversible and parallel repair
plans. Journal of Intelligent Manufacturing. To ap-
pear (DOI 10.1007/s10845-008-0162-9).
Homem de Mello, L. and Sanderson, A. (1990). And/or
graph representation of assembly plans. IEEE Trans-
actions on Robotics and Automation, 6(2):188–189.
Kolisch, R. and Drexl, A. (1999). Local for multi-mode
resource-constrained project. IIE Transactions (Insti-
tute of Industrial Engineers), 29(11):987–999.
Rossi, F., Van Beek, P., and Walsh, T. (2006). Handbook of
Constraint Programming. Elsevier.
Smith, D., Frank, J., and J´onsson, A. (2000). Bridging the
gap between planning and scheduling. Knowledge En-
gineering Review, 15(1):47–83.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
358
