
INFORMATION-THEORETIC VIEW OF CONTROL
Prateep Roy, Arben C¸ ela
Universit
´
e Paris-Est, ESIEE, D
´
epartement Syst
`
emes Embarqu
´
es, Paris, France
Yskandar Hamam
F’SATIE-TUT, Pretoria, South Africa
Keywords:
Information Theory, Shannon Entropy, Mutual-Information, Control, Bode Sensitivity Integral.
Abstract:
In this paper we are presenting the information-theoretic explanation of Bod
´
e Sensitivity Integral, a funda-
mental limitation of control theory, controllability grammian and the issues of control under communication
constraints. As resource-economic use of information is of prime concern in communication-constrained
control problems, we need to emphasize more on informational aspect which has got direct relation with un-
certainties in terms of Shannon Entropy and Mutual Information. Bode Integral which is directly related to the
disturbances can be correlated with the difference of entropies between the disturbance-input and measurable
output of the system. These disturbances due to communication channel-induced noises and limited bandwidth
are causing the information packet-loss and delays resulting in degradation of control performances.
1 INTRODUCTION
In recent years, there has been an increased interest
for the fundamental limitations in feedback control.
Bode’s sensitivity integral ( Bode Integral, in short ) is
a well-known formula that quantifies some of the lim-
itations in feedback control for linear time-invariant
systems. In (Sandberg and Bernhardsson, 2005), it is
shown that there is a similar formula for linear time-
periodic systems.
In this paper, we focus on Bode integral of control
theory and Shannon Entropy of information theory
because the latter is a stronger metric for uncertainty
which hinders control of a system.
It has been known that control theory and informa-
tion theory share a common background as both the-
ories study signals and dynamical systems in general.
One way to describe their difference is that the fo-
cal point of information theory is the signals involved
in systems while control theory focuses more on sys-
tems which represent the relation between the input
and output signals. Thus, in a certain sense, we may
expect that they have a complementary relation. For
this reason, many researchers have consecrated stud-
ies on the interactions of the two theories : Control
Theory and Information Theory.
In networked control systems, there are issues related
to both control and communication since communica-
tion channels with data losses, time delays, and quan-
tization errors are employed between the plants and
controllers (Antsaklis and Baillieul, 2007). To guar-
antee the overall control performance in such systems,
it is important to evaluate the quantity of information
that the channels can transfer. Thus, for the analysis
of networked control systems, information theoretic
approaches are especially useful, and notions and re-
sults from this theory can be applied. The results
in (Nair and Evans, 2004) and (Tatikonda and Mit-
ter, 2004) show the limitation in the communication
rate for the existence of controllers, encoders, and de-
coders to stabilize discrete-time linear feedback sys-
tems.
The focus of information theory is more on the signals
and not on their input-output relation. Thus, based on
information theoretic approaches, we may expect to
extend prior results in control theory. One such result
can be found in (Martins et al., 2007), where a sen-
sitivity property is analyzed and Bode’s integral for-
mula (Bode H., 1945) is extended to a more general
class of systems. A fundamental limitation of sensi-
tivity functions is presented in relation to the unstable
poles of the plants.
5
Roy P., Ã
˘
Gela A. and Hamam Y.
INFORMATION-THEORETIC VIEW OF CONTROL.
DOI: 10.5220/0002166600050012
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2009), page
ISBN: 978-989-674-001-6
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 PROBLEM FORMULATION
Networked control systems suffer from the drawbacks
of packet losses, delays and quantization in particular.
These cause degradation of control performances and
under some conditions instability. Uncertainties due
to packet losses, delays, quantization, communication
channel induced noises etc. have a great influence on
the system systems performance. If we consider only
the uncertainties induced by channel noise and quan-
tization we may write:
˙x(t) = Ax(t) + Bu(t) + w(t); (1)
y(t) = Cx(t) + Du(t) + v(t);
where A ∈ R
n×n
is the system or plant matrix and
B ∈ R
n×q
is the control or input matrix. Also, x(t)
is the state, u(t) is the control input, y(t) is the out-
put, C is the output or measurement matrix, D is the
Direct Feed matrix, w(t) and v(t) are the external dis-
turbances and noises of Gaussian nature respectively.
Our aim is to achieve better control perfor-
mance of system by tackling these uncertainties
using Shannon’s Mutual-Information, Information-
Theoretic Entropy and Bode Sensitivity. We present
the information-theoretic model of such uncertainties
and their possible reduction using information mea-
sures.
3 PRELIMINARIES
By means of the connection between Bode integral
and the entropy cost function, paper (Iglesias, 2001)
provided a time-domain characterization of Bode in-
tegral. The traditional frequency domain interpreta-
tion is that, if the sensitivity of a closed-loop system is
decreased over a particular frequency range typically
the low frequencies the designer ”pays” for this in in-
creased sensitivity outside this frequency range. This
interpretation is also valid for the time-domain char-
acterization presented in (Iglesias, 2001) provided
one deals with time horizons rather than frequency
ranges. Time-domain characterization of Bode’s in-
tegral shows how the frequency domain trade-offs
translate into the time-domain. Under the usual con-
nection between the time and frequency domains:
low (high) frequency signals are associated with long
(short) time horizons. In Bode’s result, it is important
to differentiate between the stable poles, which do not
contribute to the Bode sensitivity integral and the un-
stable poles, which do. Time-varying systems which
can be decomposed into stable and unstable compo-
nents are said to possess an exponential dichotomy.
What the exponential dichotomy says is that the norm
of the projection onto the stable subspace of any orbit
in the system decays exponentially as t → ∞ and the
norm of the projection onto the unstable subspace of
any orbit decays exponentially as t → −∞, and fur-
thermore that the stable and unstable subspaces are
conjugate. The existence of an exponential dichotomy
allows us to define a stability preserving state space
transformation (a Lyapunov transformation) that sep-
arates the stable and unstable parts of the system.
3.1 Mutual Information
Shannon’s Mutual information is just the information
carried by one random variable about the other. It is
a quantity in the time domain. Mutual Information
I(X;Y ), between X as the input variable and Y as the
output variable, has the lower and upper bounds given
by the following:
R(D) = RateDistortion = MinI(X;Y) (2)
C = CommunicationChannelCapacity = MaxI(X;Y )
(3)
where D is the distortion which happens when infor-
mation is compressed (i.e. fewer bits are used to rep-
resent or code more frequent or redundant informa-
tions) and entropy is the limit to this compression i.e.
if one compresses the information beyond the entropy
limit there is a high probability that the information
will be distorted or erroneous. This is as per Shan-
non’s Source Coding Theorem. We code more fre-
quently used symbols with fewer number of bits and
vice-versa.
Mutual information is also the difference of entropies,
where entropy is nothing but the measure of uncer-
tainty. Just as entropy (Middleton, 1960) in physical
systems tends to increase in the course of time, the
reverse is true for information about an information
source : as information about the source is processed,
it tends to decrease with time, becoming more cor-
rupt or noisy until it is evidently destroyed unless ad-
ditional information is made available. Here, infor-
mation refers to the case of desired messages.
3.2 Shannon Entropy
Shannon proposed a measure of uncertainty in a dis-
crete distribution based on the Boltzmann entropy of
classical statistical mechanics. He called it the en-
tropy and defined as follows.
We have to take into account the statistics of the al-
ternatives by replacing our original measure of the
number of alternatives by the more general expression
defining the entropy as follows:
H = −
∑
i
p
i
log
2
(p
i
) (4)
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
6

where p
i
is the probability of the alternative i. The
above quantity is known as the binary entropy in bits
as we use logarithmic base of 2 (with logarithmic base
e the entropy is in nats), and was shown by Shannon
to correspond to the minimum average number of bits
needed to encode a probabilistic source of N states
distributed with probability p
i
. Intuitively, H can also
be considered as a measure of uncertainty : it is min-
imum, and is equal to zero, when one of the alterna-
tives appears with probability one, whereas it is max-
imum and equals to log
2
N when all the alternatives
are equiprobable so that p
i
=
1
N
for all i.
The term entropy is associated with the uncertainty
or randomness whereas information is used to reduce
this uncertainty. Uncertainty is the main hindrance
to control and if we can reduce the uncertainty by
getting the relevant information and utilizing the in-
formation properly so as to achieve the desired con-
trol performance of the system. Many researchers
have posed the same question: How much informa-
tion is required for controlling the system based on
observed informations in the case where these infor-
mations are passed through communication channels
in a networked based system?
Mutual Information I(X;Y ) and Entropies H(X),
H(Y ) and joint entropy H(X ,Y ) are related as :
I(X;Y ) = H(X) + H(Y ) −H(X,Y)
where H(X) is the uncertainty that X has about Y ,
H(Y ) is the uncertainty that Y has about X , and
H(X,Y ) is the uncertainty that X and Y hold in com-
mon. Information value degrades over time and en-
tropy value increases over time in general. The con-
ditional version of the chain rule (Cover and Thomas,
2006) :
I(X;Y ) = H(X) −H(X|Y ) = H(Y ) −H(Y |X) ; valid
for any random variables X and Y .
Mutual information I(X;Y ) is the amount of uncer-
tainty in X, minus the amount of uncertainty in X
which remains after Y is known”, which is equivalent
to ”the amount of uncertainty in X which is removed
by knowing Y ”. This corroborates the intuitive mean-
ing of mutual information as the amount of informa-
tion (that is, reduction in uncertainty) that each vari-
able is having about the other.
The conditional entropy H(X|Y ) or read as condi-
tional entropy of X knowing Y or conditioned on Y ,
is often interpreted in communication theory as rep-
resenting an information-loss (the so-called equivo-
cation of Shannon (Shannon, 1948)), which results
from subtracting the maximum noiseless capacity
I(X; X) = H(X) of a communication channel with in-
put X and output Y from the actual capacity of that
channel as measured by I(X;Y ).
3.3 Bode Integral
Physically an intrinsically stable system needs no in-
formation on its internal state or the environment to
assure its stability. So, if we consider a well de-
signed stable feedback control system with distur-
bances or/and noises as inputs and performance sig-
nals as outputs then it not needed to have extra feed-
back loop to assure its stability. We may say the same
thing for systems which are intrinsically open-loop
stable. For example, a pendulum with non-zero fric-
tion coefficient subject to a perturbation will return
back to the equilibrium position after a transient pe-
riod without any need of extra information. For unsta-
ble systems the mutual information between the initial
state and the output of the system is related to its un-
stable poles.
The simplest (and perhaps the best known) result is
that, for an open loop stable plant, the integral of the
logarithm of the closed loop sensitivity is zero; i.e.
Z
∞
0
ln
|
S
0
( jω)
|
dω = 0
Where, S
0
and ω being the sensitivity function and
frequency respectively.
Now, we know that the logarithm function has the
property that it is negative if
|
S
0
|
< 1 and it is positive
if
|
S
0
|
> 1. The above result implies that set of fre-
quencies over which sensitivity reduction occurs (i.e.
where
|
S
0
|
< 1) must be matched by a set of frequen-
cies over which sensitivity magnification occurs (i.e.
where
|
S
0
|
> 1). For a stable rational transfer function
L ( jω), sensitivity is defined as S ( jω) =
1
1+L( jω)
. This
has been given a nice interpretation as thinking of sen-
sitivity as a pile of dirt. If we remove dirt from one
set of frequencies, then it piles up at other frequencies.
Hence, if one designs a controller to have low sensi-
tivity in a particular frequency range, then the sensi-
tivity will necessarily increase at other frequencies -
a consequence of the weighted integral always being
a constant; this phenomenon has also been called the
Water-Bed Effect (pushing down on the water bed in
one area, raises it somewhere else).
For linear systems Bode Integral is the difference in
the entropy rates between the input and output of the
systems which is an information-theoretic interpreta-
tion. For nonlinear system (if the open loop system
is globally exponentially stable and has fading mem-
ory) this difference is zero. Fading Memory Require-
ment is used to limit the contributions of the past val-
ues of the input on the output. Entropy of the signals
in the feedback loop help provide another interpreta-
tion of the Bode integral formula (Zang and Iglesias,
2003)(Mehta et al., 2006) as follows. Shannon En-
INFORMATION-THEORETIC VIEW OF CONTROL
7
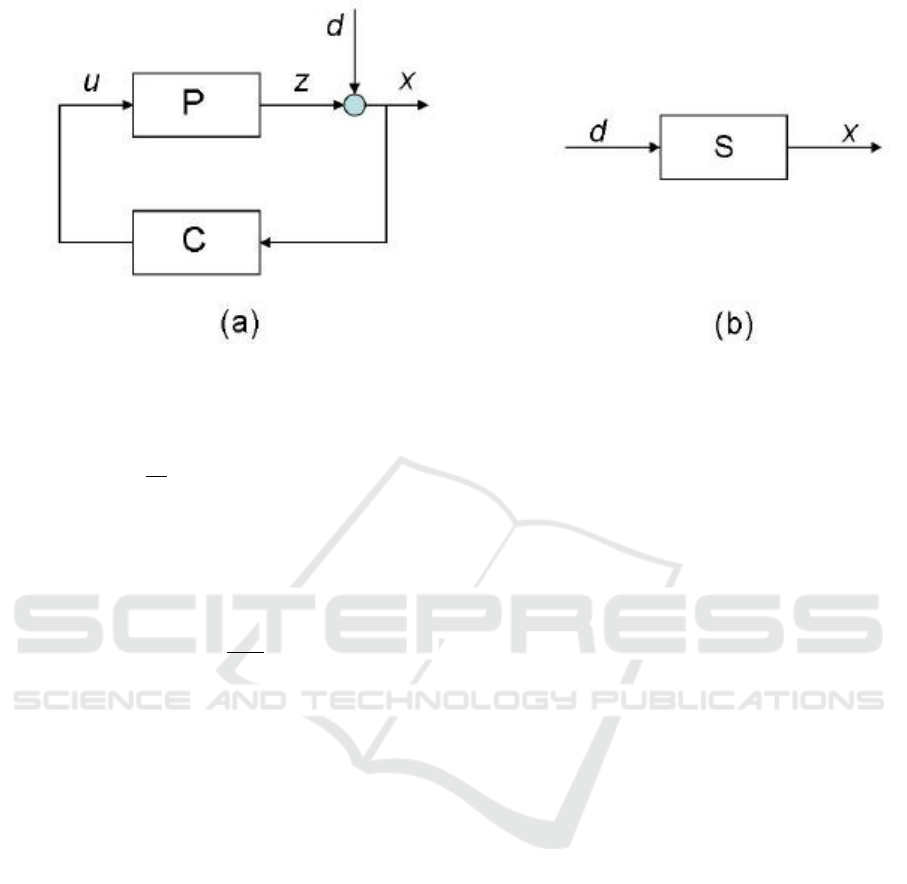
Figure 1: (a) Feedback loop and (b) Sensitivity function.
tropy - Bode Integral Relation can be rewritten as :
H
c
(x)−H
c
(d) =
1
2π
Z
π
−π
ln
S
e
jω
dω =
∑
k
log(p
k
)
(5)
Where S
e
jω
is the transfer function of the feedback
loop from the disturbance d to output x and p
k
’s are
unstable poles (|p
k
| > 1) of the open-loop plant; S is
referred to as the sensitivity function for an open-loop
plant gain P and a stabilizing feedback controller
gain C, S is given by S =
1
1+PC
. Sensitivity shows
how much sensitive is the observable output state to
input disturbance. Here, H
c
(x) and H
c
(d) denote the
conditional entropy of the random processes associ-
ated with the output x and disturbance d respectively
as per Figure1(Mehta et al., 2006).
Consider a random variable x ∈ ℜ
m
of continuous
type with entropy associated with this is given by
H(x) := −
R
ℜ
m
p(x)ln p(x)dx;
where p(x) being the probability density func-
tion of x and the conditional entropy of order n is
defined as
H(x
k
|x
k−1
,. .., x
k−n
) := −
R
ℜ
m
p(.)ln p(.)dx
where p(.) = (x
k
|x
k−1
,. .., x
k−n
).
This conditional entropy is a measure of the un-
certainty about the value of x at time k under the
assumption that its n most recent values have been
observed. By letting n going to infinity, the condi-
tional entropy of x
k
is defined as
H
c
(x
k
) := lim
n→∞
H(x
k
|x
k−1
,. .., x
k−n
) assuming
the limit exists. Thus the conditional entropy is
a measure of the uncertainty about the value of x
at time k under the assumption that its entire past
is observed. Difference of conditional entropies
between the output and input is nothing but the Bode
sensitivity integral which equals the summation of
logarithms of unstable poles.
For a stationary Markov process, conditional entropy
(Cover and Thomas, 2006) is given by
H(x
k
|x
k−1
,. .., x
k−n
) = H(x
k
|x
k−1
).
4 RELATED WORK
It is well known that the sensitivity and complemen-
tary sensitivity functions represent basic properties
of feedback systems such as disturbance attenuation,
sensor-noise reduction, and robustness against uncer-
tainties in the plant model. Researchers have worked
earlier on the issues of relating the entropy and the
Bode Integral and complementary sensitivity. Refer
to work in (Sandberg and Bernhardsson, 2005), (Mar-
tins et al., 2007), (Bode H., 1945), (Freudenberg and
Looze, 1988), (Zang, 2004), (Iglesias, 2002), (Igle-
sias, 2001), (Zang and Iglesias, 2003), (Mehta et
al., 2006), (Sung and Hara, 1989), (Sung and Hara,
1988), (Okano et al., 2008), (Jialing Liu, 2006). In
(Iglesias, 2002) the sensitivity integral is interpreted
as an entropy integral in the time domain, i.e., no
frequency-domain representation is used.
One has to gather relevant information, transmit the
information to the relevant agent, process the infor-
mation, if needed, and then use the information to
control the system. The fundamental limitation in
information transmission is the achievable informa-
tion rate (i.e. a fundamental parameter of Information
Theory), the fundamental limitation in information
processing is the Cramer-Rao Bound (CRB) which
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
8

deals with Fisher Information Matrix (FIM) in Esti-
mation Theory, and the fundamental limitation in in-
formation utilization is the Bode Integral (i.e. a funda-
mental parameter of Control Theory), seemingly dif-
ferent and usually separately treated, are in fact three
sides of the same entity as per the paper (Liu and Elia,
2006). Even Kalman et al. in their paper (Kalman et
al., 1963) have stated that Controllability Grammian
Matrix W-matrix is analogous to FIM and the deter-
minant det W is analogous to Shannon Information.
These research work motivated us to investigate some
important correlations amongst mutual information,
entropy and design control parameters of practical im-
portance rather than just concentrating on stability is-
sues.
5 INFORMATION INDUCED BY
CONTROLLABILITY
GRAMMIAN
In general, from the viewpoint of the open-loop sys-
tem, when the system is unstable, the system ampli-
fies the initial state at a level depending on the size
of the unstable poles (Okano et al., 2008). Hence, we
can say that in systems having more unstable dynam-
ics, the signals contain more information about the
initial state. Using this extra information (in terms of
mutual information between the control input and the
initial state) we can reduce the entropy (uncertainty)
and thus rendering more easy the observation of ini-
tial state.
Suppose that we have a feedback control system in
which control signal is sent through a network with
limited bandwidth. We will consider the case where
the state of the system is measurable and the con-
troller can send the state of the system without error.
Under these conditions we may write:
˙x(t) = Ax(t) + Bu
∗
(t); (6)
u
∗
(t) = −K
c
x(t) + u
e
(t);
where K
c
, u
∗
(t) and u
e
(t), represent, respectively, the
feedback controller gain, the applied control input
and control error due to quantization noise of limited
bandwidth network. In the sequel we are supposing
that the control signal errors are caused by Gaussian
White Noise which may be given by u
e
i
(t) =
√
D
i
δ(t).
So we may write :
˙x(t) = (A −BK
c
)x(t) + Bu
e
(t); (7)
u
∗
(t) = −K
c
x(t) + u
e
(t);
or more compactly:
˙x(t) = A
c
x(t) + Bu
e
(t); (8)
where,A −BK
c
= A
c
.
u
∗
(t) = −K
c
x(t) + u
e
(t);
The feedback system (8) is a stable one which is
perturbed by quantization errors or noises due to the
bandwidth limitation.
Lemma : The controllability grammian matrix
W of system (8) is related with the information-
theoretic entropy H as follows (Mitra, 1969):
H(x,t) =
1
2
ln
{
detW(D,t)
}
+
n
2
(1 + ln 2π) (9)
(Where D being the Diagonal Matrix (positive defi-
nite symmetric matrix) with D
i
being the ith diagonal
element. Here unit impulse inputs are considered.)
= Average apriori uncertainty of the state x at
time t for an order n of the system.
where
W(D,τ) =
Z
τ
0
e
A
c
t
BDB
T
e
A
c
T
t
dt
for a system modeled as (8).
Proof of Eqn.(9): Referring to (Cover and Thomas,
2006) we are providing the proof. The input of
(8) being Gaussian White Noise, the state of the
system is with probability density having mean-value
¯x(t) = e
A
c
t
x(0) and Covariance Matrix Σ at time t is
given by
Σ = E
(x − ¯x)(x − ¯x)
T
= W(D,t).
In a more detailed form :
x(t) = e
A
c
t
x(0) +
Z
t
0
e
A
c
t
Bu(t)dt
E
{
x(t)
}
= E
e
A
c
t
x(0) +
Z
t
0
e
A
c
t
Bu(t)dt
T here f ore, ¯x(t) = e
A
c
t
x(0)
where ¯x(t) denotes the mean value of x(t) and Covari-
ance Matrix
Σ = E
(x − ¯x)(x − ¯x)
T
⇒ Σ = E[
e
A
c
t
x(0) +
Z
τ
0
e
A
c
t
Bu(t)dt −e
A
c
t
x(0)
e
A
c
t
x(0) +
Z
τ
0
e
A
c
t
Bu(t)dt −e
A
c
t
x(0)
T
]
INFORMATION-THEORETIC VIEW OF CONTROL
9

Therefore, Σ =
R
τ
0
e
A
c
t
BDB
T
e
A
c
T
t
dt = W(D,τ).
where, u
i
(t) =
√
D
i
δ(t) i.e. weighted impulses
and D being the Diagonal Matrix (positive definite
symmetric matrix) with D
i
being the ith diagonal
element. Here unit impulse inputs are considered.
p(x,t) =
1
(2π)
n/2
{
detW(D,t)
}
1/2
e
[−1/2
n
(x−¯x)
T
W
−1
(D,t)(x−¯x)
o
]
(10)
Now, for multidimensional continuous case, entropy
(precisely differential entropy) of a continuous ran-
dom variable X with probability density function f (x)
( if
R
∞
−∞
f (x)dx = 1 ) is defined (Cover and Thomas,
2006) as
Differential Entropy h(X) = −
R
S
f (x) ln f (x)dx;
where the set S for which f (x) > 0 is called the sup-
port set of X.
As in discrete case, the differential entropy depends
only on the probability density of the random variable
and therefore the differential entropy is sometimes
written as h( f ) rather than h(X). Here, we call dif-
ferential entropy as H(x,t) and f (x) as p(x,t) which
are correlated as
H(x,t) = −
Z
p(x,t)ln p(x,t)dx (11)
Using equation (10) in equation (11) we get
H(x,t) = −
R
p(x,t)[−
1
2
(x − ¯x)
T
W
−1
(D,t)(x − ¯x)
−ln
n
(2π)
n/2
{
detW(D,t)
}
1/2
o
]dx
H(x,t) =
1
2
E
∑
i, j
(X
i
−
¯
X
i
)(W
−1
(D,t))
i j
(X
j
−
¯
X
j
)
+
1
2
ln[
{
(2π)
n
{
detW(D,t)
}
]
=
1
2
E
∑
i, j
(X
i
−
¯
X
i
)(X
j
−
¯
X
j
)(W
−1
(D,t))
i j
+
1
2
ln[
{
(2π)
n
{
detW(D,t)
}
]
=
1
2
∑
i, j
E
(X
j
−
¯
X
j
)(X
i
−
¯
X
i
)
(W
−1
(D,t))
i j
+
1
2
ln[
{
(2π)
n
{
detW(D,t)
}
]
=
1
2
∑
j
∑
i
(W(D,t))
ji
(W
−1
(D,t))
i j
+
1
2
ln[
{
(2π)
n
{
detW(D,t)
}
]
=
1
2
∑
j
(W(D,t))(W
−1
(D,t))
j j
+
1
2
ln[
{
(2π)
n
{
detW(D,t)
}
]
=
1
2
∑
j
I
j j
+
1
2
ln[
{
(2π)
n
}{
detW(D,t)
}
]
(Where I
j j
is the Identity Matrix )
=
n
2
+
1
2
ln[
{
(2π)
n
}{
detW(D,t)
}
]
=
n
2
+
1
2
ln
{
(2π)
n
}
+
1
2
ln
{
detW(D,t)
}
=
n
2
+
n
2
ln
{
(2π)
}
+
1
2
ln
{
detW(D,t)
}
H(x,t) =
1
2
ln
{
detW(D,t)
}
+
n
2
(1 + ln 2π)
Since Controllability Grammian is independent
of co-ordinate system and so is the Mutual Informa-
tion, we try to draw the analogy between the two.
Based on the equation (9) we can write the entropy
reduction as
∆H(x,t) =
1
2
∆[ln
{
detW(D,t)
}
]
This shows that the entropy reduction which is
same as uncertainty reduction is dependent on
Controllability Grammian only. Other term being
constant for constant n, gets canceled.
Therefore, ∆H(x,t) = H(x(t
1
),t
1
) −H(x(t
2
),t
2
)
=
1
2
ln
{
detW
1
(D
1
,t
1
)
}
−
1
2
ln
{
detW
2
(D
2
,t
2
)
}
⇒ ∆H(x,t) =
1
2
ln
detW
1
(D
1
,t
1
)
detW
2
(D
2
,t
2
)
(12)
For simplicity we denote ∆H(x,t) by ∆H, W
1
(D
1
,t
1
)
by W
1
and W
2
(D
2
,t
2
) by W
2
.
Therefore, ∆H =
1
2
ln
n
det(
W
1
W
2
)
o
⇒ det(
W
1
W
2
) = e
2(∆H)
Using the above expression along with the con-
cept of mutual information being the difference of
the entropy and the residual conditional entropy i.e.
I(X;U) = H(X ) − H(X|U) (gain in information is
reduction in entropy), we can conclude that Mutual
Information I(X ;U) between the state X and control
input U denoted simply by Shannon Information I
sh
is given by this ∆H which can be expressed further as
Finally,
det(
W
1
W
2
) = e
2(∆H)
= e
2I
sh
(13)
We may conclude that the uncertainty reduction
which is directly related to the ∆H(x,t) will reduce
the variance of the state with respect to the steady-
state if ∆H(x,t) converges to zero. The only influence
we have on the control signal is related to that of feed-
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
10

back gain, to be chosen such that the norm of grammi-
ans, represented by det(W (D
i
,t)) converge rapidly to
their norm to infinity det(W (D
∞
,∞)). We will detail
the related approach in a future paper.
6 CONCLUSIONS
This paper has addressed some new ideas concerning
the relation between control design and information
theory. Since the networked control system has com-
munication constraints due to limited bandwidth or
noises, we must have to adopt a policy of resource al-
location which enhances the information transmitted.
This may be done possible if we know the character-
istics of the networks, the bandwidth constraints and
that of the dynamical system under study.
As demonstrated the grammian of controllability con-
stitute a metric of information theoretic entropy with
respect to the noises induced by quantization. Reduc-
tion of these noises is equivalent to the design meth-
ods proposing a reduction of the controllability gram-
mian norm. In the case of bandwidth constraints it
takes its full interest which will be demonstrated in
a future paper. Future work in this direction would
be also to propose an information-theoretic analysis
for enhancing the zooming algorithm proposed (Ben
Gaid and C¸ ela, 2006) and optimal allocation of com-
munication bandwidth which maximizes the systems’
performances based on Controllability Grammians.
Illustration of these results by simulation and / or ex-
perimental verification of the theoretical approaches
is the objective of our work.
REFERENCES
Sandberg H. and Bernhardsson B.(2005), A Bode Sensitiv-
ity Integral for Linear Time-Periodic Systems, IEEE
Trans. Autom. Control, Vol. 50, No. 12, December.
Antsaklis P. and Baillieul J. (2007), Special Issue on the
Technology of Networked Control Systems, Proc. of
the IEEE, Vol. 95, No. 1.
Nair G. and Evans R.(2004), Stabilizability of stochastic
linear systems with finite feedback data rates, SIAM
J. Control Optim., Vol. 43, No. 2, p. 413-436.
Tatikonda S. and Mitter S.(2004), Control under communi-
cation constraints, IEEE Trans. Autom. Control, Vol.
49, No. 7, p. 1056-1068.
Martins N., Dahleh M., and Doyle J.(2007), Fundamental
limitations of disturbance attenuation in the presence
of side information, IEEE Trans. Autom. Control, Vol.
52, No. 1, p. 56-66.
Bode H.(1945), Network Analysis and Feedback Amplifier
Design, D. Van Nostrand, 1945.
Iglesias P.(2001), Trade-offs in linear time-varying systems
: An analogue of Bode’s sensitivity integral, Auto-
matica, Vol. 37, No. 10, p. 1541-1550.
Middleton D.(1960), An Introduction to Statistical Commu-
nication Theory, McGraw-Hill Pub., p. 315.
Cover and Thomas(2006), Elements of Information Theory,
2nd Ed., John Wiley and Sons.
Shannon C.(1948), The Mathematical Theory of Commu-
nication, Bell Systems Tech. J. Vol. 27, p. 379-423, p.
623-656, July, October.
Zang G. and Iglesias P.(2003), Nonlinear extension of
Bode’s integral based on an information theoretic in-
terpretation, Systems and Control Letters, Vol. 50, p.
1129.
Mehta P., Vaidya U. and Banaszuk A.(2006), Markov
Chains, Entropy, and Fundamental Limitations in
Nonlinear Stabilization, Proc. of the 45th IEEE Con-
ference on Decision & Control, San Diego, USA, De-
cember 13-15.
Freudenberg J. and Looze D.(1988), Frequency Domain
Properties of Scalar and Multivariable Feedback Sys-
tems, Lecture Notes in Control and Information Sci-
ences, Vol. 104, Springer-Verlag, New York.
Zang G.(2004), Bode’s integral extensions in linear time-
varying and nonlinear systems, Ph.D. Dissertation,
Dept. Elect. Comput. Eng., Johns Hopkins Univ.,
USA.
Iglesias P.(2002), Logarithmic integrals and system dy-
namics : An analogue of Bode’s sensitivity integral
for continuous-time time-varying systems, Linear Alg.
Appl., Vol. 343-344, p. 451-471.
Sung H. and Hara S.(1989), Properties of complementary
sensitivity function in SISO digital control systems,
Int. J. Control, Vol.50, No. 4, p. 1283-1295.
Sung H. and Hara S.(1988), Properties of sensitivity and
complementary sensitivity functions in single-input
single-output digital control systems, Int. J. Control,
Vol. 48, No. 6, p. 2429-2439.
Okano K, Hara S. and Ishii H.(2008), Characterization of a
complementary sensitivity property in feedback con-
trol: An information theoretic approach, Proc. of the
17th IFAC-World Congress, Seoul, Korea, July 6-11,
p. 5185-5190.
Jialing L.(2006), Fundamental Limits in Gaussian Channels
with Feedback: Confluence of Communication, Esti-
mation and Control, Ph.D. Thesis, Iowa State Univer-
sity.
Liu J. and Elia N. (2006), Convergence of Fundamental
Limitations in Information, Estimation, and Control,
Proceedings of the 45th IEEE Conference on Decision
& Control, San Diego, USA, December.
Kalman R., Ho Y. and Narendra K.(1963), Controllability
of linear dynamical systems, Contributions to Differ-
ential Equations, Vol. 1, No. 2, p. 189-213.
Mitra D.(1969), W-matrix and the Geometry of Model
Equivalence and Reduction, Proc. of the IEE, Vol.
116, No.6, June, p. 1101-1106.
INFORMATION-THEORETIC VIEW OF CONTROL
11

Ben Gaid M. M., and C¸ ela A.(2006), Trading Quantiza-
tion Precision for Sampling Rates in Networked Sys-
tems with Limited Communication, Proceedings of
the 45th IEEE Conference on Decision & Control, San
Diego, CA, USA, December 13-15.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
12
