
SUBOPTIMAL DUAL CONTROL ALGORITHMS FOR
DISCRETE-TIME STOCHASTIC SYSTEMS UNDER INPUT
CONSTRAINT
Andrzej Krolikowski
Poznan University of Technology, Institute of Control and Information Engineering, Poland
Dariusz Horla
Poznan University of Technology, Institute of Control and Information Engineering, Poland
Keywords:
Input constraint, Suboptimal dual control.
Abstract:
The paper considers a suboptimal solution to the dual control problem for discrete-time stochastic systems un-
der the amplitude-constrained control signal. The objective of the control is to minimize the two-step quadratic
cost function for the problem of tracking the given reference sequence. The presented approach is based on
the MIDC (Modified Innovation Dual Controller) derived from an IDC (Innovation Dual Controller) and the
TSDSC (Two-stage Dual Suboptimal Control. As a result, a new algorithm, i.e. the two-stage innovation
dual control (TSIDC) algorithm is proposed. The standard Kalman filter equations are applied for estimation
of the unknown system parameters. Example of second order system is simulated in order to compare the
performance of proposed control algorithms. Conclusions yielded from simulation study are given.
1 INTRODUCTION
The problem of the optimal control of stochastic sys-
tems with uncertain parameters is inherently related
with the dual control problem where the learning
and control processes should be considered simulta-
neously in order to minimize the cost function. In
general, learning and controlling have contradictory
goals, particularly for the finite horizon control prob-
lems. The concept of duality has inspired the devel-
opment of many control techniques which involve the
dual effect of the control signal. They can be sepa-
rated in two classes: explicit dual and implicit dual
(Bayard and Eslami, 1985). Unfortunately, the dual
approach does not result in computationally feasible
optimal algorithms. A variety of suboptimal solutions
has been proposed, for example: the innovation dual
controller (IDC) (R. Milito and Cadorin, 1982) and its
modification (MIDC) (Kr´olikowski and Horla, 2007),
the two-stage dual suboptimal controller (TSDSC)
(Maitelli and Yoneyama, 1994) or the pole-placement
(PP) dual control (N.M. Filatov and Keuchel, 1993).
Other controllers like minimax controllers (Se-
bald, 1979), Bayes controllers (Sworder, 1966),
MRAC (Model Reference Adaptive Controller)
(
˚
Astr¨om and Wittenmark, 1989), LQG controller
where unknown system parameters belong to a finite
set (D. Li and Fu, ) or Iteration in Policy Space (IPS)
(Bayard, 1991) are also possible.
The IPS algorithm and its reduced complexity
version were proposed by Bayard (Bayard, 1991)
for a general nonlinear system. In this algorithm
the stochastic dynamic programming equations are
solved forward in time ,using a nested stochastic ap-
proximation technique. The method is based on a spe-
cific computational architecture denoted as a H block.
The method needs a filter propagating the state and
parameter estimates with associated covariance ma-
trices.
In (Kr´olikowski, 2000), some modifications in-
cluding input constraint have been introduced into the
original version of the IPS algorithm and its perfor-
mance has been compared with MIDC algorithm.
In this paper, a new algorithm, i.e. the two-stage
innovation dual control (TSIDC) algorithm is pro-
posed which is the combination of the IDC approach
and the TSDSC approach. Additionally, the ampli-
tude constraint of control input is taken into consider-
ation for algorithm derivation.
Performance of the considered algorithms is il-
49
Krolikowski A. and Horla D.
SUBOPTIMAL DUAL CONTROL ALGORITHMS FOR DISCRETE-TIME STOCHASTIC SYSTEMS UNDER INPUT CONSTRAINT.
DOI: 10.5220/0002162500490053
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2009), page
ISBN: 978-989-674-001-6
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

lustrated by simulation study of second-order system
with control signal constrained in amplitude.
2 CONTROL PROBLEM
FORMULATION
Consider a discrete-time linear single-input single-
output system described by ARX model
A(q
−1
)y
k
= B(q
−1
)u
k
+ w
k
, (1)
where A(q
−1
) = 1 + a
1,k
q
−1
+ ·· · + a
na,k
q
−na
,
B(q
−1
) = b
1,k
q
−1
+ ··· + b
nb,k
q
−nb
, y
k
is the output
available for measurement, u
k
is the control sig-
nal, {w
k
} is a sequence of independent identically
distributed gaussian variables with zero mean and
variance σ
2
w
. Process noise w
k
is statistically inde-
pendent of the initial condition y
0
. The system (1)
is parametrized by a vector θ
k
containing na + nb
unknown parameters {a
i,k
} and {b
i,k
} which in
general can be assumed to vary according to the
equation
θ
k+1
= Φθ
k
+ e
k
(2)
where Φ is a known matrix and {e
k
} is a sequence
of independent identically distributed gaussian vector
variables with zero mean and variance matrix R
e
. Par-
ticularly, for the constant parameters we have
θ
k+1
= θ
k
= θ
= (b
1
, · ·· , b
nb
, a
1
, · ·· a
na
)
T
, (3)
and then Φ = I, e
k
= 0 in (2).
The control signal is subjected to an amplitude
constraint
| u
k
|≤ α (4)
and the information state I
k
at time k is defined by
I
k
= [y
k
, ..., y
1
, u
k−1
, ..., u
0
, I
0
] (5)
where I
0
denotes the initial conditions.
An admissible control policy Π is defined by a se-
quence of controls Π = [u
0
, ..., u
N−1
] where each con-
trol u
k
is a function of I
k
and satisfies the constraint
(4). The control objective is to find a control policy
Π which minimizes the following expected cost func-
tion
J = E[
N−1
∑
k=0
(y
k+1
− r
k+1
)
2
] (6)
where {r
k
} is a given reference sequence. An admis-
sible control policy minimizing (6) can be labelled by
CCLO (Constrained Closed-Loop Optimal) in keep-
ing with the standard nomenclature, i.e. Π
CCLO
=
[u
CCLO
0
, ..., u
CCLO
N−1
]. This control policy has no closed
form, and control policies presented in the following
section can be viewed as a suboptimal approach to the
Π
CCLO
.
3 SUBOPTIMAL DUAL
CONTROL ALGORITHMS
In this section, we shall briefly describe algorithms
being an approximate solution to the problem formu-
lated in Section 2. To this end, the method for estima-
tion of system parameters θ
k
is needed.
3.1 Estimation Method
The system (1) can be expressed as
y
k+1
= s
T
k
θ
k+1
+ w
k+1
(7)
where
s
k
= (u
k
, u
k−1
, . . . , u
k−nb+1
, −y
k
, . . . , − y
k−na+1
)
T
=
= (u
k
, s
∗
T
k
)
T
. (8)
The estimates
ˆ
θ
k
needed to implement dual control
algorithms can be obtained in many ways. A common
way is to use the standard Kalman filter in a form of
suitable recursive procedure for parameter estimation,
i.e.
ˆ
θ
k+1
= Φ
ˆ
θ
k
+ k
k
ε
k
(9)
k
k
= ΦP
k
s
k−1
[s
T
k−1
P
k
s
k−1
+ σ
2
w
]
−1
(10)
P
k+1
= [Φ − k
k
s
T
k−1
]P
k
Φ
T
+ R
e
, (11)
ε
k
= y
k
− s
T
k−1
ˆ
θ
k
, (12)
where ε
k+1
is the innovation which will be used later
on to construct the suboptimal dual control algorithm.
The following partitioning is introduced for pa-
rameter covariance matrix P
k
P
k
=
"
p
b
1
,k
p
T
b
1
θ
∗
,k
p
b
1
θ
∗
,k
P
θ
∗
,k
#
(13)
corresponding to the partition of θ
k
θ
k
= (b
1,k
, θ
∗T
k
)
T
(14)
with
θ
∗
k
= (b
2,k
, . . . , b
nb,k
, a
1,k
, . . . , a
na,k
)
T
. (15)
3.2 Two-stage Dual Suboptimal Control
(TSDSC) Algorithm
The TSDSC method proposed in (Maitelli and
Yoneyama, 1994) has been derived for system (1)
with stochastic parameters (2). Below this method
is extended for the input-constrained case. The cost
function considered for TSDSC is given by
J =
1
2
E[(y
k+1
− r)
2
+ (y
k+2
− r)
2
|I
k
] (16)
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
50

and according to (Maitelli and Yoneyama, 1994) can
be obtained as a quadratic form in u
k
and u
k+1
, i.e.
J =
1
2
[au
k
+ bu
k+1
+ cu
k
u
k+1
+ du
2
k
+ eu
2
k+1
] (17)
where a, b, c, d, e are expressions depending on cur-
rent data s
∗
k
, reference signal r and parameter esti-
mates
ˆ
θ
k
(Maitelli and Yoneyama, 1994). Solving a
necessary optimality condition the unconstrained con-
trol signal is
u
TSDSC,un
k
=
bc− 2ae
4de− c
2
. (18)
This control law has been taken for simulation anal-
ysis in (Maitelli and Yoneyama, 1994). Imposing the
cutoff the constrained control signal is
u
TSDSC,co
k
= sat(u
TSDSC,un
k
;α). (19)
The cost function (27) can be represented as a
quadratic form
J =
1
2
[u
T
k
Au
k
+ b
T
u
k
] (20)
where u
k
= (u
k
, u
k+1
)
T
, and
A =
d
1
2
c
1
2
c e
, b =
a
b
. (21)
The condition 4de − c
2
> 0 together with d > 0 im-
plies positive definitness and guarantees convexity.
Minimization of (30) under constraint (4) is a stan-
dard QP problem resulting in u
TSDSC,qp
k
. The con-
strained control u
TSDSC,qp
k
is then applied to the sys-
tem in receding horizon framework.
3.3 Two-stage Innovation Dual
Suboptimal Control (TSIDSC)
Algorithm
A modified version of the TSDSC algorithm is given
below where innovation term is included to the cost
function
J =
1
2
E[(y
k+1
− r)
2
+ (y
k+2
− r)
2
− λ
k+1
ε
2
k+1
|I
k
]
(22)
where λ
k+1
≥ 0 is the learning weight, and ε
k+1
is the innovation, see (16). Incorporating the term
−λ
k+1
ε
2
k+1
in the cost function makes the parameter
estimation process to accelerate and consequently to
improve the future control performance. Taking (2)
and (7) into account it can be seen that
ε
k+1
= s
T
k
[Φ(θ
k
−
ˆ
θ
k
) + (Φ− I)
ˆ
θ
k
] + s
T
k
e
k
+ w
k+1
,
(23)
and consequently
E[ε
2
k+1
|I
k
] = s
T
k
ΦP
k
Φ
T
s
k
+ s
T
k
(Φ− I)
ˆ
θ
k
ˆ
θ
T
k
(Φ− I)
T
+
+s
T
k
R
e
s
k
+ σ
2
w
=
= s
T
k
[ΦP
k
Φ
T
+ (Φ − I)
ˆ
θ
k
ˆ
θ
T
k
(Φ− I)
T
+ R
e
]s
k
+ σ
2
w
=
= s
T
k
Σ
k
s
k
+ σ
2
w
. (24)
Introducing the partitioning for matrix Σ
k
Σ
k
=
σ
11,k
σ
T
1,k
σ
1,k
Σ
k
∗
. (25)
Keeping (8) in mind we have
E[ε
2
k+1
|I
k
] = fu
2
k
+ gu
k
+ h, (26)
where f = σ
11,k
, g = σ
T
1,k
s
∗
k
, h = s
∗T
k
Σ
k
∗
s
∗
k
+ σ
2
w
are
expressions known at the current time instant k.
Finally, the cost function J including terms de-
pending only on u
k
and u
k+1
takes the form
J =
1
2
[au
k
+ bu
k+1
+ cu
k
u
k+1
+ du
2
k
+ eu
2
k+1
−
−λ
k+1
( fu
2
k
+ gu
k
)] (27)
Solving a necessary optimality condition the uncon-
strained control signal is
u
TSIDSC,un
k
=
bc− 2ae − 2eg
4de− c
2
− 4e fλ
k+1
. (28)
Imposing the cutoff the constrained control signal is
u
TSIDSC,co
k
= sat(u
TSIDSC,un
k
;α). (29)
The cost function (27) can again be represented as a
quadratic form
J =
1
2
[u
T
k
Au
k
+ b
T
u
k
] (30)
where u
k
= (u
k
, u
k+1
)
T
, and correspondingly to (21)
A =
d − λ
k+1
f
1
2
c
1
2
c e
, b
=
a− λ
k+1
g
b
. (31)
The weight λ
k+1
has influence on positive definitness
of the quadratic form. Minimization of (30) under
constraint (4) is again the QP problem resulting in
u
TSIDSC,qp
k
. The constrained control u
TSIDSC,qp
k
is then
applied to the system in receding horizon framework.
4 SIMULATION TESTS
Performance of the described control methods is illus-
trated through the example of a second-order system
with the following true values: a
1
= −1.8, a
2
= 0.9,
b
1
= 1.0, b
2
= 0.5, where the Kalman filter algorithm
SUBOPTIMAL DUAL CONTROL ALGORITHMS FOR DISCRETE-TIME STOCHASTIC SYSTEMS UNDER INPUT
CONSTRAINT
51
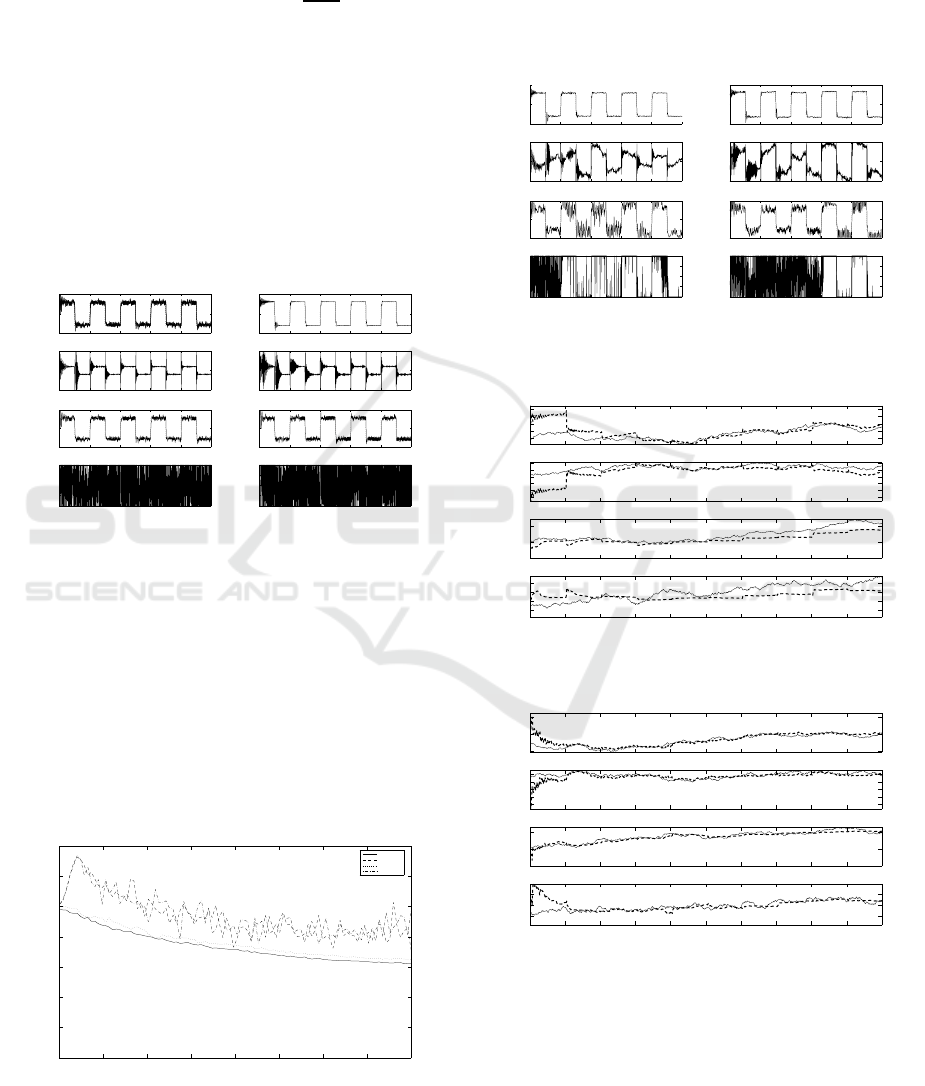
(9)-(12) was applied for estimation. The initial pa-
rameter estimates were taken half their true values
with P
0
= 10I. The reference signal was a square
wave ±3, and then the minimal value of constraint
α ensuring the tracking is α
min
= 3
|A(1)|
|B(1)|
= 0.2. Fig.
1 shows the reference, output and input signals dur-
ing tracking process under the constraint α = 1 for
both TSDSC and TSIDSC control policies. The con-
trols u
TSDSC,qp
k
and u
TSIDSC,qp
k
were obtained solving
the minimization of quadratic forms (20), (31) using
MATLAB function quadprog. The performance of
these control algorithms is surprisingly essentially in-
ferior with respect to u
TSDSC,co
k
and u
TSIDSC,co
k
. On the
other hand, as expected, the control u
TSIDSC,co
k
per-
forms better than u
TSDSC,co
k
.
0 200 400 600 800 1000
−5
0
5
k
y
k
, r
k
TSDSC co
0 200 400 600 800 1000
−5
0
5
k
y
k
, r
k
TSIDSC co
0 200 400 600 800 1000
−5
0
5
k
y
k
, r
k
TSDSC qp
0 200 400 600 800 1000
−5
0
5
k
y
k
, r
k
TSIDSC qp
0 200 400 600 800 1000
−1
0
1
k
u
k
0 200 400 600 800 1000
−1
0
1
k
u
k
0 200 400 600 800 1000
−1
−0.5
0
0.5
1
k
u
k
0 200 400 600 800 1000
−1
−0.5
0
0.5
1
k
u
k
Figure 1: Reference, output and control signals for TSDSC,
TSIDSC; α = 1; constant parameters.
For the control policy Π
TSIDSC
the constant learning
weight was λ
k
= λ = 0.98.
The performance index
¯
J =
N−1
∑
k=0
(y
k+1
− r
k+1
)
2
was considered for simulations. The plots of
¯
J versus
the constraint α are shown in Fig.2 for σ
2
w
= 0.05, and
N = 1000.
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
200
400
600
800
1000
1200
1400
α
J
TSDSC,co
TSDSC,qp
TSIDSC,co
TSIDSC,qp
Figure 2: Plots of performance indices for TSDSC,
TSIDSC.
In the case of varying parameters (2), Φ = I and
R
e
= 0.05I have been taken. Fig.3 shows the perfor-
mance of the tracking process under the constraint
α = 1 for both TSDSC and TSIDSC control poli-
cies. An examplary run of parameter estimates is
shown in Figs.4,5 for control policies TSIDSC, co and
TSIDSC, qp, respectively.
0 200 400 600 800 1000
−1
−0.5
0
0.5
1
k
u
k
0 200 400 600 800 1000
−5
0
5
k
y
k
, r
k
TSDSC, co
0 200 400 600 800 1000
−5
0
5
k
y
k
, r
k
TSIDSC, co
0 200 400 600 800 1000
−1
0
1
k
u
k
0 200 400 600 800 1000
−1
0
1
k
u
k
0 200 400 600 800 1000
−5
0
5
k
y
k
, r
k
TSDSC, qp
0 200 400 600 800 1000
−1
−0.5
0
0.5
1
k
u
k
0 200 400 600 800 1000
−5
0
5
k
y
k
, r
k
TISIDSC, qp
Figure 3: Reference, output and control signals for TSDSC,
TSIDSC; α = 1; varying parameters.
100 200 300 400 500 600 700 800 900 1000
−1.8
−1.6
−1.4
−1.2
−1
k
a
1
, a
^
1
100 200 300 400 500 600 700 800 900 1000
0.2
0.4
0.6
0.8
1
1.2
k
a
2
, a
^
2
100 200 300 400 500 600 700 800 900 1000
0.5
1
1.5
k
b
1
, b
^
1
100 200 300 400 500 600 700 800 900 1000
0.4
0.6
0.8
1
k
b
2
, b
^
2
Figure 4: Parameter estimates for TSIDSC, co.
100 200 300 400 500 600 700 800 900 1000
−2
−1.5
−1
k
a
1
, a
^
1
100 200 300 400 500 600 700 800 900 1000
0.2
0.4
0.6
0.8
1
k
a
2
, a
^
2
100 200 300 400 500 600 700 800 900 1000
0.5
1
1.5
k
b
1
, b
^
1
100 200 300 400 500 600 700 800 900 1000
0.4
0.6
0.8
k
b
2
, b
^
2
Figure 5: Parameter estimates for TSIDSC, qp.
5 CONCLUSIONS
This paper presents a problem of discrete-time dual
control under the amplitude-constrained control sig-
nal. A simulation example of second-order system is
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
52

given and the performance of the presented two con-
trol policies is compared by means of the simulated
performance index.
A new control policy TSIDSC was proposed as
suboptimal dual control approach. The method ex-
hibits good tracking properties for both constant and
time-varying unknown system parameters.
It was found that both control policies u
TSDSC,qp
k
and u
TSIDSC,qp
k
derived via QP optimization do not
yield a tracking improvement compared to the cut-off
controls u
TSDSC,co
k
and u
TSIDSC,co
k
.
REFERENCES
˚
Astr¨om, H. and Wittenmark, B. (1989). Adaptive Control.
Addison-Wesley.
Bayard, D. (1991). A forward method for optimal stochastic
nonlinear and adaptive control. IEEE Trans. Automat.
Contr., 9:1046–1053.
Bayard, D. and Eslami, M. (1985). Implicit dual control for
general stochastic systems. Opt. Contr. Appl.& Meth-
ods, 6:265–279.
D. Li, F. Q. and Fu, P. Optimal nomial dual control for
discrete-time linear-quadratic gaussian problems with
unknown parameters. Automatica, 44:119–127.
Kr´olikowski, A. (2000). Suboptimal lqg discrete-time con-
trol with amplitude-constrained input: dual versus
non-dual approach. European J. Control, 6:68–76.
Kr´olikowski, A. and Horla, D. (2007). Dual controllers for
discrete-time stochastic amplitude-constrained sys-
tems. In Proceedings of the 4th Int. Conf. on Infor-
matics in Control, Automation and Robotics.
Maitelli, A. and Yoneyama, T. (1994). A two-stage dual
suboptimal controller for stochastic systems using ap-
proximate moments. Automatica, 30:1949–1954.
N.M. Filatov, H. U. and Keuchel, U. (1993). Dual pole-
placement controller with direct adaptation. Automat-
ica, 33(1):113–117.
R. Milito, C.S. Padilla, R. P. and Cadorin, D. (1982). An
innovations approach to dual control. IEEE Trans. Au-
tomat. Contr., 1:132–137.
Sebald, A. (1979). Toward a computationally efficient opti-
mal solution to the lqg discrete-time dual control prob-
lem. IEEE Trans. Automat. Contr., 4:535–540.
Sworder, D. (1966). Optimal Adaptive Control Systems.
Academic Press, New York.
SUBOPTIMAL DUAL CONTROL ALGORITHMS FOR DISCRETE-TIME STOCHASTIC SYSTEMS UNDER INPUT
CONSTRAINT
53
