
AN INNOVATIVE EDUCATIONAL ENVIRONMENT FOR THE
INTERACTIVE LEARNING OF DATA STRUCTURES
From Algebraic Specification to Implementation
Rafael del Vado V
´
ırseda
Dpto. de Sistemas Inform
´
aticos y Programaci
´
on, Universidad Complutense de Madrid, Spain
Keywords:
Virtual learning environments, Virtual universities and classrooms, Learning and teaching methodologies,
Computer supported education, Interactive learning, Data structures, Algorithmic schemes, Algebraic specifi-
cation.
Abstract:
The high level of abstraction necessary to teach “data structures” and “algorithmic schemes” have been more
than a hindrance to students. In order to make a proper approach to this issue, we have developed and imple-
mented, during the last years, at the Computer Science Department of the Complutense University of Madrid,
an innovative interactive learning system according to the new guidelines of the European Higher Education
Area. In this paper, we present the new main contributions to this system. In the first place, we describe
the tool called Vedya for the visualization of data structures and algorithmic schemes. In the second place,
the Maude system to execute the algebraic specifications of abstract data types using Eclipse, by which it is
possible to study from the more abstract level of a software specification up to its specific implementation in
Java, thereby allowing the students a self-learning process.
1 MOTIVATION
The study of “data structures” and “algorithmic
schemes” constitute one of the essential aspects of the
academic formation of every engineer in Computer
Science. Nevertheless, the high level of abstraction
necessary to teach these topics occasionally hinders
its understanding to students. In order to make a
proper approach to this issue, we have developed and
implemented, during the last years, at the Computer
Science Department of the Complutense University of
Madrid, an innovative interactive learning system ac-
cording to the new guidelines of the European Higher
Education Area and the teaching model focused on
the student.
In this paper, we present the two main contribu-
tions to this system. On the one hand, the Vedya tool
(Segura et al., 2008), a visualization tool by means
of which it is possible to provide the student with a
complete learning system of both the main data struc-
tures and the more relevant algorithmic schemes. On
the other hand, the Maude system (Clavel and et al.,
2006) for the execution of “algebraic specifications”
of abstract data types using the language of formal
specification provided by this system.
Thanks to the development environment Eclipse
(http://www.eclipse.org/ ), we have obtained a fully
complete system that is useful for the students as well
as the professors, that allows to go from the most
abstract level of data structures, provided by its al-
gebraic specification in Maude, until its specific im-
plementation in a modern programming language as
happens with Java. All this learning process can be
guided and overseen in a completely autonomous way
by using the Vedya tool, through which it is possible
to make enquiries about the documentation related to
each of the algebraic specifications, to distinguish bet-
ween the behavior of the structure and its different im-
plementations through the use of different views or to
browse information regarding the cost of the different
implementations that have been proposed.
2 THE VEDYA TOOL
Vedya is an integrated interactive environment for
learning data structures and algorithmic schemes. It
covers the most common data structures: Stacks,
queues, binary search trees, AVL trees, priority
queues, and sorted and hash tables. Moreover, it also
provides other different types of abstract data types,
like one for an implementation of a “doctor’s office”.
27
del Vado Vírseda R. (2009).
AN INNOVATIVE EDUCATIONAL ENVIRONMENT FOR THE INTERACTIVE LEARNING OF DATA STRUCTURES - From Algebraic Specification to
Implementation.
In Proceedings of the First International Conference on Computer Supported Education, pages 27-32
DOI: 10.5220/0001844900270032
Copyright
c
SciTePress
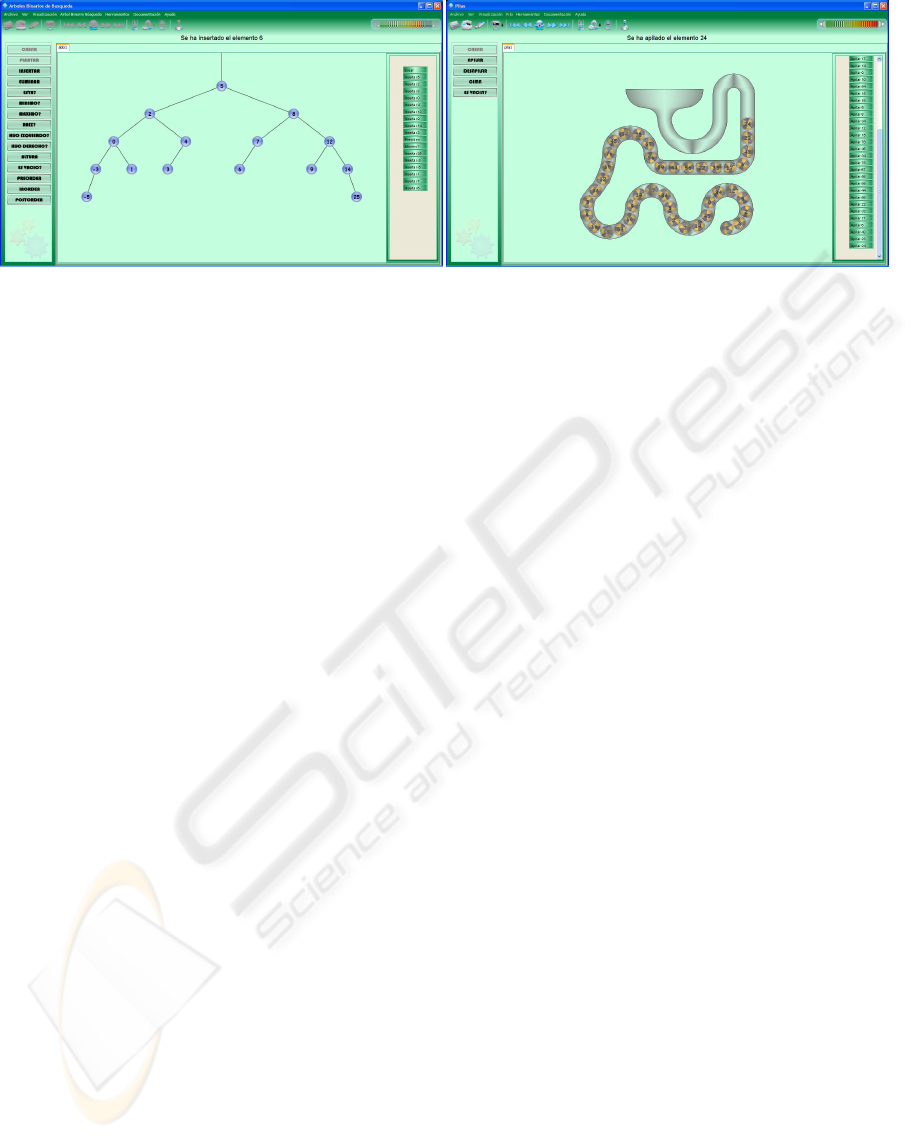
Figure 1: Data structures and algorithmic schemes in the Vedya tool.
Concerning the algorithmic schemes, it covers the
most common resolution methods (Brassard and Brat-
ley, 1996; Cormen et al., 2001; Neapolitan and Naim-
pour, 2003): divide and conquer, dynamic program-
ming, backtracking, and branch and bound. All data
structures and algorithmic schemes taught in the re-
lated study courses are thereby integrated in the same
environment: Vedya allows the execution of different
data structures and several sequences of operations on
the same structures at the same time making use of a
multi-windows and multi-frame system.
Currently, there are two versions of the Vedya tool.
The first version contains all the data structures and
algorithmic schemes mentioned above while the new
one offers a subset of them in a more attractive vi-
sual environment. This last version can be found at
http://www.fdi.ucm.es/profesor/rdelvado/.
There are several options to use this tool. The
main one is the interactive execution, but it is also
possible to create simulations that are automatically
executed, to visualize tutorials and to solve tests
within the same environment. It also integrates a set
of animations that show how data structures are used
to solve certain problems. Figure 1 shows an example
of the main windows for data structures (stacks and
binary trees). The central panel is used to represent
the structure. In the case of linear structures and bi-
nary trees, drawing facilities are offered to allow the
expansion or contraction of the data structure or to
move it over the screen to see the hidden parts. On the
left, there is a list of the actions that can be executed.
Partial non-allowed actions are disabled. The right
panel shows the visualization of the actions that have
been already executed. Next, the user may continue
executing actions, go up on the sequence of actions to
see previous states or she/he may use the stimulation
facilities (standard buttons to execute, stop, move for-
ward and move backwards at the top of the screen) to
restart the sequence from the beginning. Notice that
just above the central panel the result of the last action
is shown.
There are two types of views: The one of data
structure behavior to intuitively comprehend its ope-
ration, and one or several implementation views, ei-
ther static or dynamic. On Figure 1 we show the spe-
cific behavior view of a stack. Representations of the
static implementation based on an array and dynamic
implementation based on pointers can be also shown.
Furthermore, the environment provides documen-
tation about algebraic specification, the implementa-
tion code and the cost of each implementation. On the
top of the screen, there is a menu that facilitates mana-
ging the system. We can create a new data structure,
open an existing one or save the state of the editing
one. We can also execute the operations on the data
structure, use the simulation facilities and change the
execution speed of the animations.
The main window for the execution of algorith-
mic schemes looks similar. We have implemented
algorithmic schemes based on divide and conquer
of binary search and quicksort; algorithmic schemes
that solve backtracking problems (in its fractional and
non-fractional version) based on dynamic program-
ming; branch and bound, as well as the Dijkstra algo-
rithm to obtain minimum path in a graph.
As has been previously mentioned, Vedya is
complemented with tutorials on data types (stacks,
queues, binary search trees, red-black trees, prior-
ity queues, and 2-3-4 trees) and animations of algo-
rithms that show the use of a data structure to solve a
problem (evaluation of an expression in postfix form,
the transformation of an infix expression to a postfix
one, breath-first tree transversal, checking of palin-
dromes). Moreover, there are animations on graphs:
To obtain the minimum spanning tree using the Prim
and Kruskal algorithms and to compute minimum
paths using the Dijsktra algorithm.
Finally, Vedya offers the Vedya-Test tool to solve
CSEDU 2009 - International Conference on Computer Supported Education
28

fmod STACK{X :: TRIV} is fmod QUEUE{X :: TRIV} is
sort Stack{X} . sort Queue{X} .
op error : -> Stack{X} . op error : -> Queue{X} .
op error : -> X$Elt . op error : -> X$Elt .
op empty : -> Stack{X} . op empty : -> Queue{X} .
op push : X$Elt Stack{X} -> Stack{X} . op enqueue : Queue{X} X$Elt -> Queue{X} .
op pop : Stack{X} -> Stack{X} . op dequeue : Queue{X} -> Queue{X} .
op top : Stack{X} -> X$Elt . op first : Queue{X} -> X$Elt .
op isEmpty? : Stack{X} -> Bool . op isEmpty? : Queue{X} -> Bool .
var P : Stack{X} . var C : Queue{X} .
var E : X$Elt . var E : X$Elt .
eq pop(empty) = error . eq dequeue(empty) = error .
eq pop(push(E,P)) = P . ceq dequeue(enqueue(C,E)) = empty if isEmpty?(C) .
eq top(empty) = error . ceq dequeue(enqueue(C,E)) = enqueue(dequeue(C),E))
eq top(push(E,P)) = E . if not isEmpty?(C) .
eq isEmpty?(empty) = true . eq first(empty) = error .
eq isEmpty?(push(E,P)) = false . ceq first(enqueue(C,E)) = E if isEmpty?(C) .
endfm ceq first(enqueue(C,E)) = first(C)
if not isEmpty?(C) .
eq isEmpty?(empty) = true .
eq isEmpty?(enqueue(C,E)) = false
endfm
Figure 2: Algebraic specifications of stacks and queues in Maude.
tests. This tool can be independently executed
and allows teachers to create, modify or delete
questions in a database, and to create tests from
the database of questions. The student visualizes
the tests, solves them and obtains the correct so-
lutions. Questions are grouped by subject-matter
on the database, but it is possible to mix ques-
tions about different data structures in the same test.
The last version of this tool can be also found at
http://www.fdi.ucm.es/profesor/rdelvado/.
3 EXECUTION OF ALGEBRAIC
SPECIFICATIONS IN MAUDE
For the execution of algebraic specifications, the lan-
guage Maude (Clavel and et al., 2006) based on
rewriting logic has been used. Maude is a high-
level language and high-performance system support-
ing both equational and rewriting computation for a
wide range of applications. Maude and its formal tool
environment can be used in three mutually reinfor-
cing ways: as a declarative programming language,
as an executable formal specification language, and as
a formal verification system. Moreover, (Clavel and
et al., 2006) describes the equational specification of
the data structures included in the Vedya tool now in
Maude syntax (stacks, queues, lists, binary and search
trees, AVL and 2-3-4 trees). The language is available
for Linux and MacOS at http://maude.cs.uiuc.edu, and
there are also extensions for its execution in Windows
at http://moment.dsic.upv.es.
The specifications can be executed in Eclipse
(http://www.eclipse.org/ ) by means of special “plug-
ins” developed in the Department of Information Sys-
tems and Computation of the Technical University of
Valencia (DISC-UPV) and in the Computational Lan-
guages and Sciences Department of the University of
M
´
alaga (DLCC-UMA). This environment facilitates
the student its usage by integrating the text editor with
the execution commands of the system. On the left,
there appear the developed projects; the central part
shows the editor and the execution panel of the sys-
tem is on it; on the inferior part, the control panel that
shows the result of the action. On the right part, the
user can open other windows that allow the definition
of different system options and depuration.
The basic element of a specification in Maude is
a “module”. The language allows defining the func-
tional modules used to define the data types; system
modules used to define rewriting systems and modu-
les focused on objects that allow the usage of syn-
tax of classes, objects and messages. The functional
modules for stacks and queues are showed with more
detail in Figure 2.
The language allows importing other modules,
defining several data types, defining operations on the
types and equations that define the behavior of those
operations. The modules can be customized, using
“theories” to such end in order to define the parame-
ters and “views” to relate the formal parameter to the
real parameter. The system has predefined the abstract
data types most commonly used, as well as the most
common theories and views:
AN INNOVATIVE EDUCATIONAL ENVIRONMENT FOR THE INTERACTIVE LEARNING OF DATA
STRUCTURES - From Algebraic Specification to Implementation
29

view Int from TRIV to INT is
sort Elt to Int .
endv
fmod STACK-INTEGERS is
including STACK{vInt} .
endfm
fmod QUEUE-INTEGERS is
protecting QUEUE{Int} .
endfm
As can be observed, the syntax is similar to the one
used in several texts of algebraic specifications of data
types (Weiss, 1998).
In order to execute the specification, the student
enters the text in the editor; then, she/he executes the
Maude system using the existing buttons in the con-
sole and enters the module. The system detects exis-
ting syntax errors and shows them on the console.
Once the module shows no more errors, the student
may reduce terms by using the equations of the modu-
le. To such end, the student may use the commands
chart placed at the top of the screen or she/he may
directly write the command in the editor and enter it
into the system. For example, in order to obtain the
first of a queue, we can reduce the term:
red first(enqueue(enqueue(empty, 5),4)).
This term must be reduced over the module of the
queues using the integer number theory INT. In our
example, this module is named: QUEUE-INTEGERS.
The possibility of reducing terms, in an automatic
way, allows the students to carry out an initial test
of their specifications by detecting many of the errors
committed when defining the operations using equa-
tions.
Another greater advantage of executing the speci-
fications is that the student comprehends the diffe-
rence between the parameterized module and the ins-
tantiated module by being able to reduce terms on
different modules. For example, a new module could
be named QUEUE-CHARACTERS on which terms of type
red first(enqueue(enqueue(empty, ’a’),’c’)).
can be easily reduced.
During the last academic courses, we have
done practical classes on the data structures
included in Vedya, which can be found at
http://www.fdi.ucm.es/profesor/rdelvado/.
Other examples of data types, such as “medieval
queues” or a “doctor’s office” were also proposed
(Weiss, 1998). In all of them, the aim was to define
parameterized or instantiated data type with different
theories. The practical classes are complemented with
different terms that the student must reduce over some
type of instantiated modules to prove the specifica-
tion, as well as proposals to make little changes in
some actions or erroneous definitions to detect them.
Taking into consideration that students from the
second year were involved, just a few of the lan-
guage facilities have been used. In superior courses
where students have more knowledge on the subject,
a richer language can be used (Clavel and et al., 2006)
(e.g., many-sorted equational specifications, order-
sorted equational specifications, equational attributes,
and membership equational logic specifications).
4 FROM SPECIFICATION TO
IMPLEMENTATION
The Vedya tool turns into a pedagogical instrument
of high practical interest since it attempts to address
the whole self-learning process of the main data struc-
tures, from the algebraic specification in Maude until
the possible implementations in Java, within such a
powerful and integrated environment as the one that
has been described in the previous section by means
of the Eclipse system.
The students have their first contact with the data
structures that they are going to study by means of
the usage of Vedya. For example, if their learning of
data structures is focused on binary search trees or li-
near data structures, they will start learning the corres-
ponding section of the tool, where they will be able to
experiment, freely and on their own, each one of the
actions offered by these structures (see Figure 1). In
order to strengthen and evaluate this intuitive know-
ledge, the student has, in addition, the possibility of
using the Vedya-Test tool.
Once the student has a clear idea of the informal
behavior of the data structure, she/he may start work-
ing on the Eclipse system. The first step would be: to
formally capture that intuitive knowledge she/he has
obtained through the usage of Vedya in a specific al-
gebraic specification written in Maude syntax. In or-
der to facilitate this difficult step in the student’s self-
learning, she/he may use, interactively, the documen-
tation that is included in the manual of the Vedya tool.
Once the specification (see Figure 2) is entered into
the Eclipse system, the student can now go on exe-
cuting little tests using Maude, in order to check
whether it coincides with the intuitive and informal
notion of data structure from which he initially de-
parted in Vedya. Such experience would allow the
student to reach the high level of abstraction that is
necessary in computer supported education for each
formal specification of a software component, always
based on the intuitive and experimental knowledge.
CSEDU 2009 - International Conference on Computer Supported Education
30

Stacks 1 Stacks 2 Queues Sequences BST AVL RB Heaps
Group A (130) 76.4% 82.5% 77.8% 65.6% 82.2% 84.9% – 86.3%
Group B (59) 78.9% 83.6% 85.0% 63.6% 86.2% 87.7% 90.9% 90.2%
Group C (131) 76.2% 79.8% 73.5% 69.0% 83.5% – 68.9% 86.8%
2002/03 2003/04 2004/05 2005/06 2006/07 2007/08
Not attended 57.6% 45.3% 42.3% 64.7% 50.8% 40.2%
Passed 15.3% 22.2% 20.2% 18.2% 30.1% 42.6%
Failed 27.1% 32.5% 37.5% 17.1% 18.9% 17.2%
Figure 3: Students answering the tests and percentage of correct answers.
Once the algebraic specification of the data struc-
ture is obtained, the next step would be to develop an
implementation in an object-oriented programming
language such as Java, by means of the facilities pro-
vided by the programming environment in Eclipse.
This time, the student may use the algebraic specifica-
tion that she/he has built, as if dealing with an authen-
tic “instructions manual”. The main advantage of our
methodology is that the specification behaves now as
a prototype of the data structures to be implemented,
in a way that the student is able to find out the ex-
act behavior for all those moments of doubt that may
appear during the design process, even before she/he
is able to compile the program. In order to be able to
guide, in a more specific way, the step of specification
to implementation, the student may make use again of
the Vedya tool. This time, the student may access to
the part that would correspond with the implementa-
tion of data structure that she/he is studying from the
options menu (see Figure 1). From there, she/he may
try different implementation possibilities based on ar-
rays or pointers.
Once the student is familiar with the different im-
plementations of the structure, she/he is finally ready
to properly decide on a suitable representation in the
Java language. The possibility of having understood
and previously evaluated the different implementa-
tions by means of Vedya allows the student the possi-
bility to acquire a clear knowledge of the algorithmic
cost of the chosen implementation in Java for each
specific operation of the data structure, so that this
would also be a decisive criterion at the moment of
designing its own implementations. In this part, the
“algorithmic schemes” part of the Vedya tool plays an
important role, since it allows the student to acquire a
good programming methodology.
5 EVALUATION
In order to obtain a detailed evaluation of the usage of
Vedya and Maude in our integrated system, we have
proposed several tests related to the behavior, speci-
fication, implementation and application of the main
data structures offered by the tool. We also collect stu-
dents’ opinion using Vedya in the “Data Structures”
academic subject at the second year, and in the “Pro-
gramming Methodology and Technology” subject at
the third year, respectively.
The vast majority of our engineering and com-
puter science students have taken an introductory pro-
gramming course in the first academic year, typically
in Pascal. Although the learning of the main algo-
rithmic schemes and programming techniques is not a
prerequisite to the subject of “Data Structures”, many
students choose to take it either prior to, or concur-
rent with, “Programming Methodology and Techno-
logy”. As a result, although a pseudocode program-
ming language is the assumed language for “Data
Structures”, many students have enough knowledge
about C++ or Java programming languages through
the integrated programming laboratories of parallel
academic courses and subjects.
Taking into account this profile, skills and back-
ground of our engineering and computer science
students, we have proposed 8 tests in the Virtual
Campus of the Complutense University of Madrid
(http://www.ucm.es/campusvirtual/CVUCM/). The
number of engineering students registered in the Vir-
tual Campus was just over 320 distributed in three
groups (130 in group A, 59 in group B, and 131 in
group C). Figure 3 shows the number of the students
who answered each of the tests in the corresponding
group.
We observe that, from the second test on, the num-
ber of students becomes stable in a number lightly low
to the number of students who access regularly to the
Virtual Campus. These numbers, though seemingly
high, are only between 23 % (75 students of 320) and
AN INNOVATIVE EDUCATIONAL ENVIRONMENT FOR THE INTERACTIVE LEARNING OF DATA
STRUCTURES - From Algebraic Specification to Implementation
31

37 % (118 of 320) of registered students, which shows
the high rate of students giving up in this topic from
the beginning.
Figure 3 also shows the percentage of correct ans-
wers in the three groups: In general, it is high, which
demonstrates the interest of the students who have
taken part. In group B, the percentage is slightly
higher than groups A and C; since 85 % of the stu-
dents who have decided to complete the tests across
the Virtual Campus of group B are not “new” students
of this academic subject.
Figure 3 shows the percentage of students that did
not attend the final exam, those who passed, and those
who failed during the last six years. We observe that
in the last academic courses, in which we have ap-
plied the Vedya tool, we have reduced by 14% the
percentage of students giving up the course with res-
pect to the previous course, and at the same time,
we have increased by 12% the percentage of students
that passed the exam. The percentage of students that
failed the exam increased by 2% due to the rise of
students attending the exam. Comparing with previ-
ous courses (2003 to 2004) the percentage of students
that passed has increased between 8% (with respect
to the course 2003/04) and 15% (with respect to the
course 2002/03).
6 CONCLUSIONS
In this paper, we have described the usage of an in-
novative educational environment for the interactive
learning of data structure and algorithmic schemes by
means of the visualization tool called Vedya and the
specification language Maude with its programming
environment in the Eclipse system.
In the last years, many papers on visualization of
data structures and algorithms have been written. For
example, a tool with a similar style is presented in
(Chen and Sobh, 2001). Nevertheless, there is a lack
in many of them of a graphic user interface of data
structures and algorithms or they can only be executed
in a few operative systems. In this sense, Vedya is
something more than a simple tool for the execution
of data structure as has been shown in Section 2 and
(Segura et al., 2008).
The application of Vedya and Maude in a com-
plete system as Eclipse allows the students the possi-
bility of acquiring the capacity of implementing, cor-
rectly and properly, a data structure according to its
formal algebraic specification, using in their design,
the proper algorithmic schemes. As a consequence, it
is possible to provide the students with a complete
and professional methodology of software develop-
ment that is very useful in the current teaching of
Computer Science.
During the academic courses 2006/07 and
2007/08, we have carried out a detailed study in class-
room on the application of this innovative educational
environment by the Virtual Campus of the Com-
plutense University of Madrid, in the “Data Struc-
ture” and “Programming Methodology and Techno-
logy” courses corresponding to the second and third
academic courses of Computer Science.
As future work, we plan to design an Intelligent
Tutoring System in order to guide the interactive self-
learning process of data structures from the algebraic
specification to the real implementation.
ACKNOWLEDGEMENTS
This work has been partially supported by the Spanish
National Projects FAST-STAMP (TIN2008-06622-
C03-01), MERIT-FORMS (TIN2005-09027-C03-03)
and PROMESAS-CAM (S-0505/TIC/0407).
REFERENCES
Brassard, G. and Bratley, P. (1996). Fundamentals of algo-
rithms. Prentice Hall.
Chen, T. and Sobh, T. (2001). A tool for data structure
visualization and user-defined algorithm animation. In
Frontiers in Education Conference.
Clavel, M. and et al. (2006). All about maude. A high per-
formance logical framework. In How to Specify, Pro-
gram and Verify Systems in Rewriting Logic, LNCS.
Springer.
Cormen, T., Leiserson, C., Rivest, R., and Stein, C. (2001).
Introduction to Algorithms. The MIT Press.
Neapolitan, R. and Naimpour, K. (2003). Foundations of al-
gorithms using C++ pseudocode. Jones and Bartlett.
Segura, C., Pita, I., del Vado, R., Saiz, A. I., and Soler,
P. (2008). Interactive Learning of Data structures and
algorithmic schemes. In ICCS, volume 5101 of LNCS,
pages 800–809. Springer.
Weiss, M. (1998). Data Structures and Problem Solving
Using Java. Addison-Wesley.
CSEDU 2009 - International Conference on Computer Supported Education
32
